基于数字孪生的飞机起落架健康管理技术

2023-07-29郭丞皓于劲松宋悦尹琦李佳璇

航空学报 2023年11期

郭丞皓，于劲松， *，宋悦，尹琦，李佳璇

1.北京航空航天大学自动化科学与电气工程学院，北京 100191

2.航空工业成都飞机工业（集团）有限责任公司，成都 610073

根据欧洲航空安全局（European Union Aviation Safety Agency，EASA）2021 年度安全审查报告［1］显示，2020 年商业飞机起飞、降落和着陆过程在飞行阶段的事故占比可达到63.4%，军用飞机占比可达到73.5%，在这3 个阶段中由于起落架故障引起的非人为事故比例又可达到50%以上。飞机起落架作为重要支持系统，负责承受载荷、吸收冲击能量、保证飞机在地面运动过程中的使用安全，因此起落架健康程度密切影响飞机起降性能和运行安全［2］，对起落架进行实时、准确、可靠的健康管理十分必要。

现代飞机起落架是一个由若干关联的子系统共同组成的复杂综合系统，传统的维修检查方式耗费大部分时间用于定位缺陷，通常需要一系列的拆卸组装过程［3］，且不具备预测能力，维护频率为每年一次（C-check）或是更少，因此亟需对飞机起落架系统开展全面的健康管理研究以降低维修成本并提高系统可靠性和安全性［4-5］。预测和健康管理（Prognostics and Health Management，PHM）技术因有效降低复杂机电设备生命周期的维修成本而得到大力发展［6］。针对飞机起落架系统PHM 技术，现有方法主要包括基于专家系统、基于模型和基于数据驱动3 类：Yang［7］提出了基于专家系统的系统部件特征分析故障预测方法；Holmes 等［8］通过精确的非线性回归模型证明了记录的飞机飞行参数与起落架产生的载荷之间的相关性，利用飞机降落数据训练贝叶斯多层感知网络以估计起落架侧向载荷，为故障预测提供依据；Byington 等［9］提出了一种基于神经网络的起落架健康状况评估方法；Chen 等［6］提出了改进模糊C 均值算法以监测起落架收放系统健康状态；Dziendzikowski 等［10］利用运行载荷检测系统分析不同阶段对起落架疲劳磨损的影响，以实现对飞机的视情维修；Sartor 和Schmidt［11］概述了一种用于起落架结构的载荷监测方法，利用运动学模型和载荷监测数据分析起落架在其生命周期任意时刻的疲劳状态，从而预测剩余使用寿命。

面对日益复杂的飞机起落架系统，基于专家系统的健康管理方法暴露出知识不完备、规则难以配置的问题，而基于数据驱动的方法面临由于故障数据稀缺而导致的数据不平衡、解释性不强的难题，因此采用基于模型的方法以贴合对象物理机制，挖掘健康知识，建立对象系统的数字模型既作为数据平衡来源，也作为信息支撑，服务于诊断预测等健康管理任务，为系统视情维修和状态评估提供决策支持。

然而基于模型的方法往往由于系统的动态演化过程无法精确描述而限制了诊断预测等任务的准确率。近年来，随着信息物理系统（Cyber-Physical System，CPS）的发展［12］，数字孪生（Digital Twin，DT）驱动的PHM 技术［13］应用而生，其在信息空间中建立一个物理实体或真实系统的数字化模型，根据物理世界的反馈不断更新或自我学习，完成对系统的高度映射，从而全面地监测评估系统的参数指标，降低产品全生命周期管理的难度，可靠高效地完成健康管理任务［14］，解决传统PHM 技术知识不完备、数据不平衡和模型固化等问题［15］。

在DT 驱动的PHM 技术领域，国内外学者开展了多方面的研究。Wang 等［16］针对高压釜从有限元仿真角度出发，利用网格法计算生成数据，但该种方法所建立的数字孪生模型用来补充缺失的故障数据仅仅是对物理世界的模拟，缺乏与物理世界的动态交互，难以描述系统在全生命周期的健康演化过程；Li［12］、Ye［17］等通过建立动态贝叶斯网络（Dynamic Bayesian Networks，DBN）跟踪时间相关变量的演化，并校准时间无关变量，用于未来机翼或航天器结构的裂纹预测，以DBN 为方式建模考虑了模型的更新问题，但建模难度高、计算复杂，面对大型复杂系统需要严密烦琐的建模推理过程；Piltan 等［18］针对轴承设计了一种反馈反推观测器用于信号的建模估计，利用改进支持向量机算法分析残差实现故障分类，但实际系统的健康状态往往需要综合考虑多状态量，在数据源多维的场景具有一定局限性。

综上分析，现有数字孪生驱动的健康管理技术缺少模型动态更新问题的可靠解决途径，同时在基于模型的诊断预测方案设计方面存在一定局限。因此本文提出一种基于数字孪生的健康管理技术框架及具体应用方法，旨在起落架健康管理领域克服传统PHM 技术的缺点，尝试为DT驱动的PHM 技术提供一种新思路。

1 数字孪生驱动的起落架健康管理框架

根据美国国家航空航天局（National Aero‐nautics and Space Administration，NASA）2020年技术分类报告［19］，基于数字孪生的PHM 技术以高保真物理模型为基础，集成综合运载器健康管理（Integrated Vehicle Health Management，IVHM）系统的传感数据、历史数据实现状态评估从而使系统具有全面的诊断和预测能力。因此总结DT 驱动的PHM 在实际工程应用时问题主要集中于以下3 方面：

1）如何建立高保真的数字孪生模型，以解决专家知识不完备、数据驱动方法数据不平衡或解释性不强的问题。

2）如何进行数字孪生模型动态自更新，以保持与真实系统的镜像一致性，解决传统模型方法模型固化的问题。

3）如何充分利用真实系统传感数据与模型信息设计可靠的诊断预测方案，解决现有DT 驱动的PHM 技术在健康管理任务方案设计方面的难题。

本文提出基于数字孪生的起落架健康管理技术应用框架示意图（见图1），从物理和行为2 个维度建立起落架数字孪生模型，基于强化学习算法根据系统真实传感测量更新健康表征参数以完成交互层的模型跟踪任务，利用孪生模型的数据支撑、状态估计等健康信息完成服务层诊断预测等健康管理任务，以观测-更新-利用的方式覆盖起落架系统全生命周期的健康管理，最后以收放系统为例，通过实验验证该方法在具体应用时所展现的实时性、准确性、鲁棒性方面的优势。

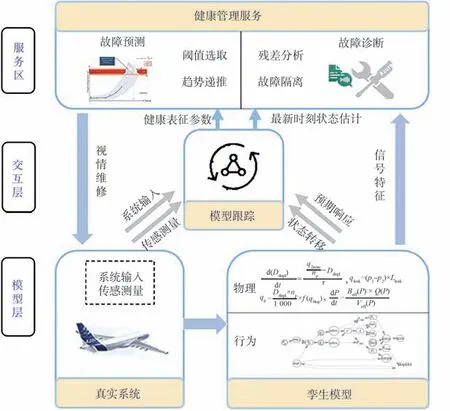
图1 基于数字孪生的起落架健康管理框架Fig.1 Landing gear health management framework based on digital twin

2 起落架数字孪生健康管理技术

针对数字孪生驱动的健康管理框架中所论述的3 个问题，给出如下的起落架数字孪生健康管理技术路线，从孪生模型建立、孪生模型更新、孪生模型利用3 个角度开展飞机起落架数字孪生健康管理技术应用研究。

2.1 起落架数字孪生模型建立

数字孪生模型是本文起落架健康管理框架的基础与核心，其既作为数据平衡的来源提供系统预期响应，也作为健康信息的来源支撑诊断预测等任务。因此本文从物理和行为2 个维度分别建立数学模型与因果图模型，模拟真实系统运行，描述系统状态行为，完成对物理世界的映射。

2.1.1 基于物理机制的起落架数学模型

从系统动力学出发，以物理机制作为建模依据，描述系统工作过程，建立预期输出与真实系统响应保持一致的起落架数学模型。

对起落架进行子系统层级的划分，基于物理机制描述系统或部件的连续状态变化。以起落架收放系统为例，其关键部件包括液压泵、作动筒、各类阀门等。

液压泵在工作过程中可视为简化的压力调节泵，由变量活塞缸、恒压阀组成。

其泵内流量取决于泵两端的压差和轴转速，流量-压力特性公式为

式（1）可近似为一个分段函数，在压力设定点即最大全流量前后服从不同压力系数。在起落架收放过程中，泵入口压差泵入口压差ppump≤pt时泵保持全流量输出，实现快速移动；pt≤ppump时恒压阀通过调节阀芯位置控制出口排量，使得出口压力稳定在预设值，即

式中：q2nom为泵内流量；ppump为泵入口压差；pt为压力设定点即最大全流量；k1、k2为压力设定点前后液压泵流量服从的不同压力系数；pmax为零流量输出压力；V为液压泵排量，mL/r；np为泵轴转速，r/min；kq、kp分别为流量比例因子、压差比例因子，作为气蚀和磨损等形式的健康表征参数。

液压泵内排量Ddispl由一阶微分方程计算

式中：τ为泵排量一阶时间常数函数。

出口流量可视为结合了泵容积效应的有效流量，计算公式为

式中：qp为泵出口流量；f(q0top)用以转换参考压力下到给定压力下的泵出口流量。

轴上转矩由泵排量和压差计算得出

式中：Ttorque为泵轴上转矩；η为机械效率因子，作为气蚀和磨损等形式的健康表征参数。

最后，设置流量比例因子、压差比例因子、机械效率因子来模拟泵气蚀或磨损等退化形式。

作动筒以主起收放作动筒为例分析工作机制，作动筒在工作过程中可视为双液压腔、单杆千斤顶和带无弹性止动件的液压缸的组合，工作过程可用公式描述为

式中：p1、p2为作动筒两端压力；A1、A2分别为压力作用横截、环形面积；Mmass为作动筒移动块总重；g为重力；θ为作动筒与水平面角度；Fforce为作用在作动筒上的合力；Ccoul为库仑摩擦力，vvis为黏滞摩擦系数；v、aacce分别为作动筒质量块的线性一维速度、加速度；Lleak为泄露系数，Beff(P)为当前压力p1、p2下的有效体积模量计算函数；Q(P)为当前压力下进入作动筒容腔的净流量转换函数；Veff(P)为当前压力下作动筒容腔有效体积计算函数；qleak为泄露流量；Vvol1为一端腔室内的流体体积；Finflow1为一端腔室内的入口流量；q1、q2为一端腔室的端口流量；Ddead1为一端死区体积。

基于物理机制建立各类阀门及收放系统其他部件模型，确定部件耦合关系，关联不同部件间输入输出，给定系统输入，基于物理公式计算推导得到起落架系统状态量及输出量，模拟其循环工作过程，将其作为数学模型，以此为依据模拟真实系统运行。

2.1.2 基于行为过程的起落架因果图模型

数学模型以物理机制为依据模拟真实系统运行，是孪生模型在物理维度上对真实系统的映射，但其关于对象的信号传递、行为过程描述不全面。飞机起落架作为多能域复杂系统，有必要对其进行简化，抽象到信号层级，在行为维度完成对真实系统的映射。

NASA 提出一种从系统键合图［20］模型中转化得到的时间因果图（Temporal Causal Graph，TCG）［21］模型，该模型本质上一种信号流图，明确捕获了故障对系统变量的影响征兆［22］从而实现定性故障诊断。本文省略键合图推导阶段，从2.1.1 节中建立的基于物理机制的起落架数学模型中转化得到简化后的因果图模型范式。

因果图模型M的组成元素包括顶点与连接线，顶点代表系统变量，连接线代表变量间的能量转移关系，其方向表示变量间的因果关系。根据因果图模型范式定义［23］，给出因果图模型概念为

式中：V为变量集合，由5 个不相交的集合组成。包括：U为输入集合，代表系统已知循环输入量；X为状态变量集合，系统动力学过程由该集合中的元素描述；Y为输出集合，对应于系统可测量的响应输出量；Θ为参数（常量）集合，代表系统不可变常量参数，用以计算系统状态量，如作动筒泄露系数Lleak，活塞杆弹性模量E=207 GPa、泊松比μ=0.3 等；A为辅助变量集合，用以辅助模型的构建和解析，如泵内排量微分变量Ddispldot=d(Ddispl)/dt；C为约束集合。每个约束c=(εc，Vc)∈C由一个包含变量Vc(Vc∈V)的方程εc组成，其用于明确变量间因果关系。

明确模型定义后，以起落架收放系统为例，从2.1.1 节物理机制数学模型中以正则匹配划分变量集合，明确系统变量因果关系，梳理约束条件，得到其部分因果图模型如图2 所示。

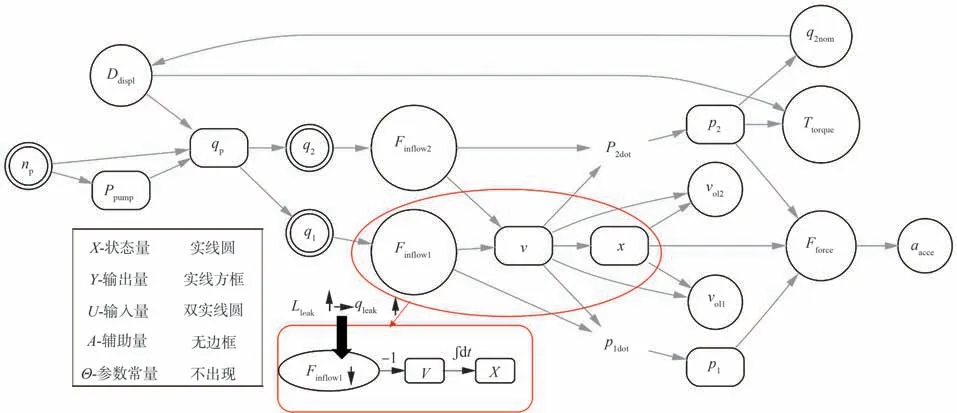
图2 起落架收放系统因果图模型Fig.2 Causal model of landing gear extension/retraction system

2.2 起落架数字孪生模型自更新

为应对传统基于模型的健康管理方法所存在模型固化的问题，采用基于强化学习算法的孪生模型自更新方法，将模型跟踪问题视为实时参数更新问题，以保持与真实系统的镜像一致性。

在本文起落架应用场景下，真实系统向孪生模型提供循环输入值与传感输出量，孪生模型通过强化学习算法在最优控制策略指导下更新调节相关健康表征参数，使得孪生模型有效跟踪真实系统响应，完成物理世界对孪生模型的交互。

在缩小与真实系统的响应偏差后，孪生模型可以继续提供最新时刻的系统状态估计，为故障预测任务提供准确、可靠、实时的系统健康信息，从而为视情维修等进一步的健康管理任务提供决策支持，完成孪生模型对物理世界的交互。

以往关于参数标定的研究大多从控制领域或统计领域发展起来的概率或估计方法出发，但这些方法普遍存在基础模型不完整［24-26］、计算成本过高、效率低等多方面的问题；近年来基于数据驱动的端对端映射方法解决了效率问题，但其把跟踪问题转化为有监督学习［27］，过分依赖于训练数据集的质量与体量，且在新场景应用时需要重新训练，在大规模系统级应用或存在较大测量噪声的条件下表现一般。综合实时性、准确性、鲁棒性多方面的考虑［28］，本文利用基于强化学习的模型跟踪方法，通过最优控制策略修正孪生模型健康表征参数，实现模型自更新。

2.2.1 马尔可夫决策过程建模

飞机起落架孪生模型（Digital Model，DM）在模拟系统物理行为的过程中，在输入ut、健康表征参数θt下，提供了系统真实输出量yt的最佳估计，同时根据状态方程得到系统状态量的最佳估计，因此模型跟踪问题可描述为

强化学习框架将跟踪问题通过马尔可夫决策过程（Markov Decision Process，MDP）建模［28］，应用最大熵深度强化学习算法来训练一个智能体agent，如式（14）所示，agent 通过找到最优控制策略选择动作，即更新孪生模型健康表征参数，以保持模型响应与观测值的匹配，最终达到式（15）的跟踪目标。

在如上的问题描述下，起落架模型跟踪MDP 模型可通过五元组(S，A，C，Τ，ρ)描述。其中S为状态集，包括系统输出量、状态量、输入量，即，以收放系统为例，确定状态集S为

式中：下标a1、a2、a3 分别代表主起收放作动筒、主起下位锁、主起上位锁；下标p 表示液压泵。

A为动作集，即系统需要跟踪的健康表征参数θt，选取跟踪参数，kp为泵压差比例因子，其值影响泵排量、转矩等过程；为主起收放作动筒泄漏系数，其值影响作动筒行程、速度等；为主起收放作动筒粘滞摩擦系数，其值影响作动筒收放时间等。

C(s，a，s′)为奖励/成本函数，用以评估跟踪效果，定义奖励函数为系统真实状态值xt、yt与预测值的均方根误差（Root Mean Squared Er‐ror，RMSE）。

Τ(s，a，s′)=p(s′|s，a)为状态转移函数，对应于所建立数字模型的动态过程

式中：f、h分别为状态转移方程和观测方程；ρ(s)为初始状态概率分布。

2.2.2 基于AC 算法的参数更新过程

采用AC（Actor-Critic）算法，以起落架孪生模型作为训练环境，提供系统动力学过程，agent根据环境反馈计算奖励，寻求最优控制策略来选择下一步动作，即跟踪参数θt+1。Actor 和Critic 网络被建立以求解最优控制策略，由Critic 网络完成基于值函数（Valuebased）的策略评估，即对当前策略π所对应的状态值函数和动作值函数的直接估计

根据Critic 网络对值函数的估计由Actor 网络完成基于策略梯度（Policy Gradient-based）的策略优化，即最大化累计奖励折扣函数

式中：r(st，at)为时间t处根据状态集st、动作集at设置的自定义奖励函数；γ∈[0，1)为折扣因子；π为当前策略；Ετ～ρ为当前策略下的状态转移信息熵分布计算；J(π)为累计折扣奖励。给出AC 算法伪代码如算法1 所示。

算法1 强化学习AC 算法Algorithm 1 Reinforcement learning AC algorithm

如图3 所示，以孪生模型作为训练环境，指导agent 进行迭代训练，同步更新Actor 和Critc 网络，并最终收敛得到最优控制策略，实际部署时应用当前最优控制策略，根据真实系统循环输入与传感输出实时修正孪生模型相关健康表征参数θt，从而平稳跟踪系统响应。

图3 基于强化学习的模型跟踪过程Fig.3 Model tracking process based on reinforcement learning

图4 残差分析与符号生成Fig.4 Residual analysis and symbol generation

2.3 基于起落架数字孪生模型的诊断预测方案

围绕起落架孪生模型开展诊断、预测等健康管理任务，充分利用模型信息，而不依赖于局限的专家知识或大体量的有监督训练集数据，并同时兼顾实时性、准确性、鲁棒性等方面的优势。

在诊断阶段，孪生模型既作为标称观测器提供预期响应输出供残差分析，也作为故障事件分析的知识库组织信号特征向量供故障隔离，最终从故障事件的角度出发完成诊断任务。

在预测阶段，经过自更新的孪生模型提供系统最新时刻的状态估计，为基于粒子滤波的状态量递推提供健康信息，结合失效阈值函数完成失效循环次数概率分布估计。

2.3.1 基于事件的故障诊断方案

1）故障事件信号特征提取

以起落架收放系统为例，根据2.1.2 节的因果图模型，分析故障机制，列举主要故障模式，对于每个故障事件f，给定其故障特征集合Sf={S1，S2，…，Sn}，其中Si=(y：smagnitude，sslope)为因果图输出集合Y中系统响应变量在当前故障事件下的信号分析元组，smagnitude，sslope∈{0，+，−}用以定性地捕获监测到残差时信号的幅度、斜率的预期变化方向。以图2 中局部放大图为例，作动筒泄漏导致作动筒inflow1下降且趋势递增，表现为“−+”；经“−1”反向传播后，因vdot与inflow1无直接关系，在作动筒v上表现为“+0”，作动筒放下速度提升；再经积分关系后，在x上表现转化为“+−”。

在因果图上执行前向传播函数［29-30］得起落架系统典型故障事件信号特征表如表1，表中信号优先级顺序（Measurement Orderings，MO）针对于当前故障事件，由因果图中因果顺序得出。

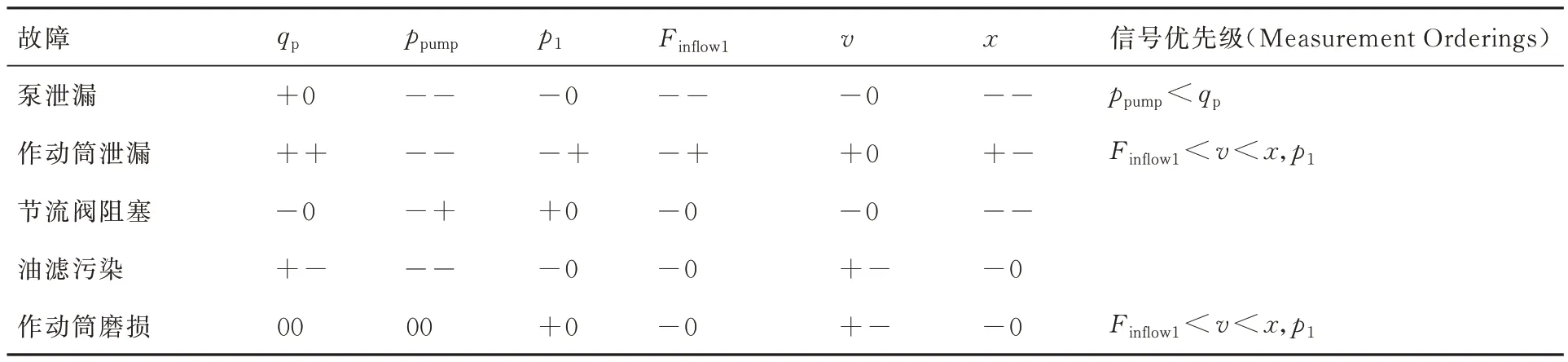
表1 起落架收放系统故障事件特征Table 1 Landing gear retraction system failure event signature

2）残差分析与符号生成

3）故障隔离

传统基于因果图的故障隔离方案随着系统响应测量信号的到来逐步隔离故障，并最终收敛至可靠故障候选集。本文希望在故障隔离后保留多个故障候选项的置信度估计，因此提出基于编辑距离的模糊匹配故障隔离方案。

编辑距离（Levenshtein Distance）指两字符串间相互转化所需的最少编辑操作次数，编辑操作包括插入、替换、删除。随着真实系统工作过程中传感信号的到来，进行Z 检验下的残差分析生成信号特征符号，组织当前系统响应特征向量，与表1 中的故障事件向量相匹配，通过动态规划算法解得各故障事件与当前特征向量的相似度（Fuzzy Matching Scores）。给出基于编辑距离的模糊匹配算法伪代码如算法2 所示。

通过编辑距离算法给出当前系统特征向量与各故障事件下的特征向量模糊匹配分数，设定置信度分数阈值，高于阈值的故障事件作为故障候选项，从而完成故障隔离任务。图5 给出了基于事件的诊断方案整体流程。

图5 故障诊断流程Fig.5 Fault diagnosis process

2.3.2 基于粒子滤波的故障预测方案

在系统健康管理领域，预测的任务集中在预测组件何时会失效。基于模型的方法将预测问题简化为联合状态参数估计问题，这种预测方法往往面临较大的不确定性，粒子滤波算法因其广泛的适用性、易于实现性、对不确定性管理的支持而成为常用的选择之一［32-34］。

算法2 基于编辑距离的模糊匹配故障隔离算法Algorithm 2 Fuzzy matching fault isolation algorithm based on levenshtein distance

在数字孪生健康管理框架下，经过自更新后的模型可以为粒子滤波算法提供当前时刻接近于真实物理世界的系统初始响应估计及后续可靠动态过程，进而完成故障预测任务。

将式（17）、式（18）起落架孪生模型动态过程扩充为

由此将强化学习马尔可夫建模过程中的状态转移函数转化为一个健康表征参数θ(t)以未知的方式演化的一般非线性模型。健康表征参数θ(t)初始值由模型自更新阶段推理得出，利用更新后的模型产生截至时间tp的观测序列，使用该观测序列给定时间点tp的故障失效时间（End Of Life，EOL）预测。EOL 在对系统级应用场景而言应定义为部件不再满足一组功能要求之一的时间点［34］，该功能要求可以用一个阈值来表示，超过这个阈值即认为组件失效，将该阈值表示为系统状态和参数的函数，具体函数为

基于粒子滤波算法的故障预测可分为以下2 个步骤［33］。

1）当前时刻状态估计

粒子滤波器中的状态分布近似于一组离散的加权样本，近似为

2）状态变量的趋势外推与估计

根据文献［3］，对起落架应用场景而言，将“循环次数”作为指标衡量剩余使用寿命或故障失效时间更为合理。以步骤1）中的联合状态参数估计p(xk，θk|y0：k)作为k时刻系统的最新知识，得到向前n步的近似状态参数预测分布为

向外递推n步结束一次循环，重复过程，可将EOL 预测近似为

以起落架收放系统为例，设定其未来输入轨迹以表示实际系统的循环收放工作过程。在该假设未来输入轨迹下，采用重要性重采样（Sampling Importance Resampling，SIR）方法实现粒子重采样步骤，在单步重采样过程对参数θ进行随机游走，应用状态方程f完成新状态的采样过程；根据观测方程h指定粒子权重，赋予接近真值的粒子更高的权重。权重归一化后基于均匀分布选取权重累计分布函数（Cumulative Distribution Func‐tion，CDF）继续执行重采样过程，围绕高权重粒子不断执行演化。给出SIR 伪代码如算法3 所示。

以式（29）、式（30）为阈值函数，将每个粒子向前递推至其EOL，最终得到所有粒子到达EOL 的循环次数概率分布。

式中：max(Pp)为液压泵压力最大值；max(qp)为泵流量最大值；max(xa1)为作动筒位移最大值；t(xa1)为作动筒收起放下时间；max(Finflow_a1)为作动筒端口流量最大值。

算法3 重要性采样（SIR）Algorithm 3 Sampling importance resampling

3 实验验证与结果分析

以起落架收放系统为例，依托于起落架数字孪生健康管理技术，对建立的数字孪生模型开展验证，并以观测-更新-利用的路线设计相关实验开展验证，证明本文所述方法在具体应用时所展现的实时性、准确性、鲁棒性方面的优势。

3.1 数字孪生模型可靠性验证

1）真实系统仿真验证

因可公开的起落架真实数据集有限，从研究角度出发，本文利用仿真数据代替真实数据开展实验验证。以起落架收放系统为例，基于AMESim 软件建立其仿真模型代替真实系统，通过仿真手段完成对真实系统不同阶段下的工作过程模拟。参照胡晓青等［35］的研究，搭建起落架收放系统模型如图6（a），给出具体参数表如表2，以其在3D Motion 下的动画模拟效果（见图6（b））及在正常收放工况下的结果（见图6（c））验证AMESim 仿真模型的有效性。

表2 AMESim 仿真模型参数Table 2 AMESim simulation model parameters

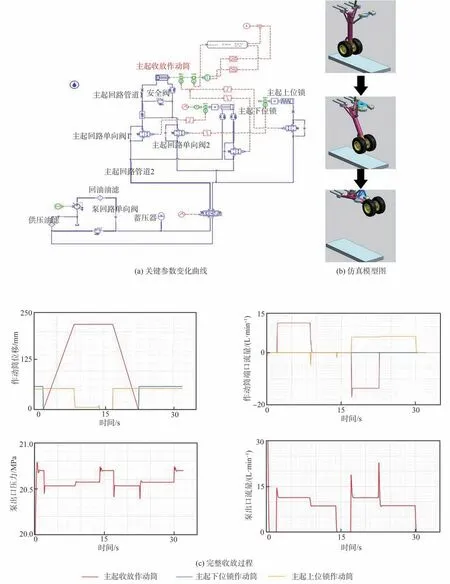
图6 AMESim 仿真模型有效性说明Fig.6 Validity description of AMESim simulation model

在如图6（a）所设计起落架仿真模型下，仿真结果如图6（c）所示，0～2 s 液压泵开始工作，调节泵出口压力稳定至20.7 MPa；2～9 s，电磁换向阀换至“左位”，液压泵出口压力下降至20.4 MPa 左右，出口流量增至11.3 L/min 附近，在压力油作用下上/下位锁打开锁钩并驱动收放作动筒开始“收起”动作，9 s 时作动筒到位；14 s时液压泵压力回升至20.7 MPa，电磁换向阀换至“中位”到17 s；17～27 s，电磁换向阀换至“右位”，作动筒开始“放下”动作；27 s 后，压力回升，电磁换向阀保持“中位”。

由仿真结果可知在正常工作模式下，起落架收起放下时间在所设计的6～10 s 范围内，各部件响应符合性能指标，并在与3D Motion 联合调试中展现了如图6（b）所示完整的收起放下过程，因此，基于AMESim 软件建立的仿真模型代替真实系统进行后续实验验证具有一定的说服力。

2）孪生模型可靠性验证

以AMESim 中建立的主起落架收放系统液压回路作为真实系统，将其输出与2.1.1 节中所建立的物理机制数学模型的响应进行对比，以关键参数变化曲线说明2.1.1 节数学模型的正确性，以联合仿真展现的完整收放过程进一步论证从2.1.1 节数学模型中所推出的因果图模型的可靠性。以液压泵出口流量和作动筒入口流量为例，上述2 个参数的正确性直接决定了主起落架收放回路工作过程的正确性，如图7所示，2.1.1节数学模型得到的关键部件输出与AMESim 模型中仿真状态量基本保持一致，因此可基于本文建立的起落架数字孪生模型开展健康管理应用任务。

图7 孪生模型可靠性说明Fig.7 Reliability description of digital twin model

3.2 健康管理任务实验验证

为论证本文所述基于数字孪生的起落架健康管理技术应用价值，设计相关实验，相继开展诊断、更新、预测验证，实验环节相互承接，诊断阶段根据孪生模型与真实系统残差进行分析隔离，更新阶段通过对健康表征参数的更新缩小故障出现后理想孪生模型与真实系统出现的偏差，预测阶段利用孪生模型最新时刻的状态估计完成失效时间估计。图8 为健康管理任务实验流程示意图。

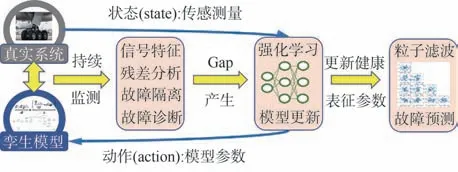
图8 实验验证流程图Fig.8 Experimental verification flow chart

3.2.1 故障诊断实验验证

以AMESim 模型的输出作为故障诊断过程中的真实信号，以2.1 节数字孪生模型作为标称观测器。如图9 所示，在不同的故障模拟下，基于事件的故障诊断方法在因果图中标记的状态量上表现出不同的故障征兆，图9（a）为通过调节主起收放回路中节流阀的孔径完成的节流阀堵塞故障模拟，图9（b）为调整泄漏系数完成的作动筒泄漏故障模拟。在图9（a）中，t=7～8 s 的状态量差异仅被诊断器判断为延迟，t=22～25 s 处的变化被诊断器判断为异常，将置信区间设置为0.95，在Z 检验下得到式（31），即‘+slope’，结合残差幅值得到此时故障特征为‘−magnitude+slope’；同理，在图9（b）中，故障特征判断为‘−magnitude−slope’。

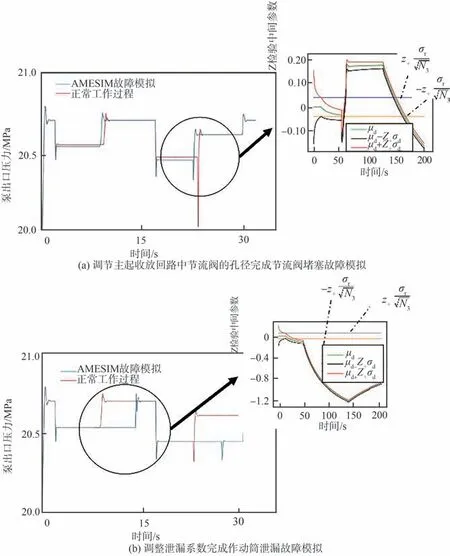
图9 Z 检验残差分析结果Fig.9 Z-test residual analysis results

以作动筒泄漏故障为例完成故障诊断实验，随着工作过程中信号的到来，结合信号优先级顺序组织故障特征向量，利用编辑距离算法与故障特征（见表1）中各故障事件征兆向量匹配，动态规划解得相似度分数，得到故障候选集，并保留置信度估计。

因果图本质上是一种信号流图，而TEAMSRT 算法作为一种基于多信号流图的经典故障诊断算法也得到了广泛应用［36］，通过建立起落架收放系统的多信号流图，利用TEAMS-RT 算法分析故障-测试性矩阵（D）和测试向量，建立对照实验。给出2 种算法故障隔离效果的比较如表3 所示，由表可知，在本文所述应用场景下，相比于多信号流图模型‘01’模式的D矩阵，因果图模型在更精确的征兆符号下，实时性、准确性表现更优，并以85 分作为置信阈值，保留了模糊集的置信度估计。

表3 故障诊断算法比较Table 3 Comparison of fault diagnosis algorithms

3.2.2 孪生模型自更新实验验证

承接故障诊断实验环节，检测到异常并正确隔离故障后，为跟踪真实系统状态响应，采用强化学习框架修正孪生模型健康表征参数，从而为后续健康管理任务提供状态估计等系统健康信息。

实验过程主要分为训练和部署2 个步骤：①利用数字孪生模型为训练过程产生模拟数据，在迭代训练过程后得到最优控制策略；②通过AMESim 产生真实系统在不同工况下的模拟仿真数据，部署当前最优控制策略，完成模型跟踪的实验验证。

由3.2.1 节的故障诊断过程确定当前系统故障为作动筒泄漏，设计以作动筒泄漏系数作为跟踪参数的实验。以2.1 节建立的数字孪生模型产生在给定负载输入条件下，作动筒泄漏系数leak 以均等步长范围，从0 变化到5×105L⋅min−1⋅Pa−1的500 条系统收放工作过程轨迹，作为强化学习AC算法训练集。

如图10 神经网络结构所示，本文使用全连接神经网络作为强化学习框架中的Critic 网络和Actor 网络，每层256 个神经元，以ReLU 作为激活函数，以Adam 作为优化器，网络超参数设置如表4。

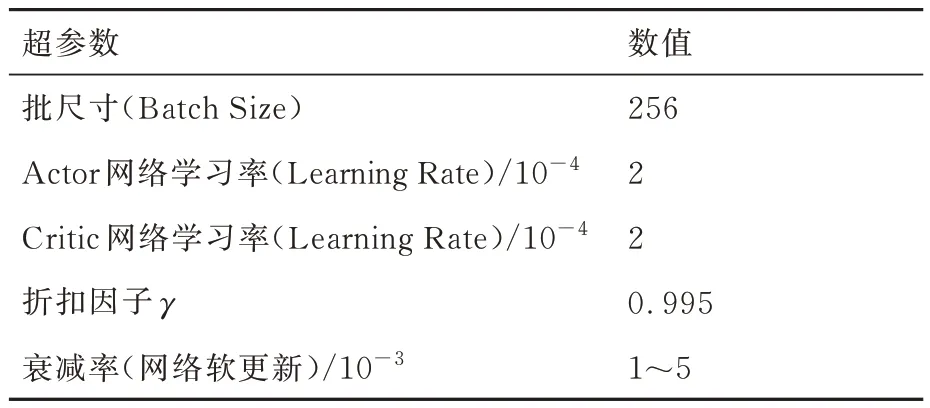
表4 网络超参数设置Table 4 Network hyperparameter settings

图10 强化学习AC 算法网络结构Fig.10 Reinforcement learning AC algorithm network structure

在100 万步的迭代训练过程后保存模型最优控制策略，图11 给出了当前策略在整体训练集上的表现以及在随机抽取的数据轨迹上的具体效果。由图11（a）可知，在整体训练集上，算法控制参数保持在真值附近，由图11（b）可看出在随机抽取的数据轨迹的具体表现上，在当前控制策略下跟踪参数轨迹中位数与真值贴近，上下四分位数也在合理范围内，但仍有部分离群点出现，分析是因为起落架收放系统在一次工作过程循环中的开始结束阶段输出量保持稳定，与系统所更新健康表征参数关联性不强，因此在这2 个阶段，当前强化学习的控制策略无法给出合理跟踪值导致出现离群点。

图11 强化学习AC 算法训练阶段效果Fig.11 Reinforcement learning AC algorithm training stage

通过AMESim 仿真模型代替真实系统生成作动筒泄漏实验数据，将系统工作循环输入和传感测量输出量作为当前最优策略的输入，不断更新孪生模型健康表征参数，完成模型自更新应用验证，实验结果如图12 所示。如图所示，部署阶段在最优控制策略的作用下，孪生模型预期输出与真实系统响应贴近，基本保持对物理世界映射的镜像一致性。

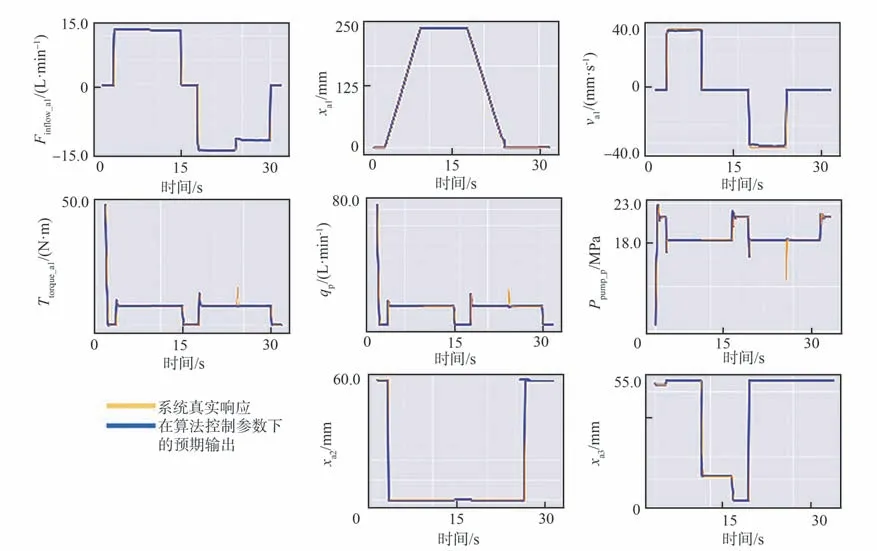
图12 强化学习算法验证效果Fig.12 Reinforcement learning algorithm verification results

本文同时搭建深度神经网络（Deep Neural Networks，DNN）的端对端直接映射神经网络，采取与强化学习算法完全一致的实验环境作为对照实验，DNN 网络结构如图13 所示。

图13 DNN 网络结构Fig.13 DNN network structure

给出在本文所述应用场景下2 种算法的性能对比见表5，由表可知，强化学习AC 算法相比端对端有监督学习方法，在实际应用时部署速度更快，误差（RMSE）更小，且在一定噪声干扰下仍能保持较好的效果，其在实时性、准确性、鲁棒性方面表现效果均优于DNN。

表5 模型跟踪算法对比Table 5 Model tracking algorithm comparison

3.2.3 故障预测实验验证

承接模型自更新环节，根据3.2.2 节的模型自更新结果，修正孪生模型健康表征参数，更新系统状态转移方程和观测方程，以模型跟踪收敛至稳定值为起点，得到系统当前时刻最新初始状态

图14 以收放系统主起作动筒为例给出了围绕模型自更新完成后系统初始状态在SIR 过程下粒子的随机游走过程，在给定状态量随机游走方差下，结合后验传感测量值分配权重，得到下一时刻粒子分布，与实际真值接近。

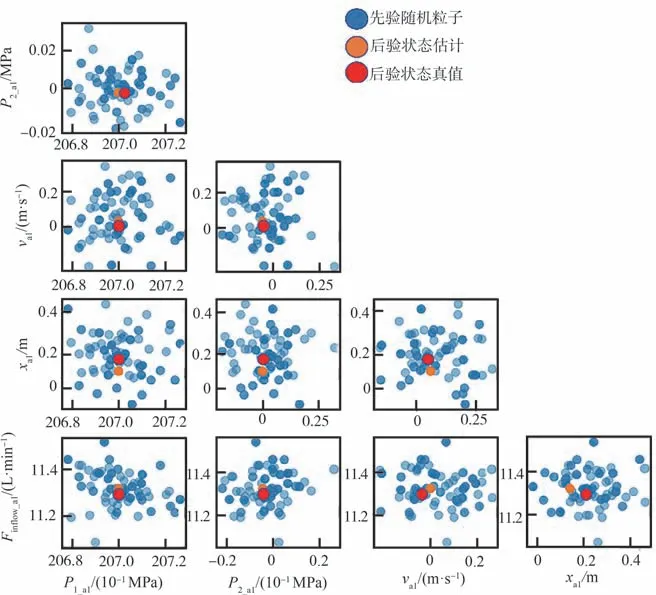
图14 初始状态单步估计Fig.14 Initial state single-step estimation

为选取最优算法参数以保证故障预测准确率，设计相关对比实验，表6 给出在不同粒子数目和随机游走方差下粒子滤波算法的表现效果。由表可知，粒子数量减少和随机游走方差的增大会造成状态估计的准确性下降，但对于主起收放作动筒最大位移0.219 4 m 和最大流量11.87 L/min 的状态量xa1、Finflow_a1，RMSE 不会造成明显的状态估计偏差。

表6 预测算法实验效果Table 6 Prediction algorithm experiment results

从当前时刻的状态估计向外递推状态量趋势，完成本次收放过程推理；之后假定系统遵循相同收放过程输入循环完成失效循环次数预测。

泄露系数Lleak在0.1 衰减系数的假定下，当前状态故障下的系统率先达到作动筒失效阈值函数，确定系统到达EOL 的循环次数概率分布如图15（a）所示，系统预测分布概率总和为1，预计将在第31 个工作循环中达到失效条件。由图15（b）中的AMESim 中的仿真结果可知，31 个循环后在5×105L ⋅min−1⋅Pa−1的泄漏系数下，作动筒放下时间超出式（30）阈值范围达到失效条件，由此可知预测结果与实际仿真结果基本保持一致。