一种结合壁面模型模拟湍流流动的间断界面浸入边界法

2023-07-29张仕钊吴杰杨德武丛歆雨

航空学报 2023年11期

张仕钊，吴杰，杨德武，丛歆雨

南京航空航天大学航空学院空气动力学系，南京 210016

近年来，一种名为浸入边界法（IBM）的处理方法引起了人们的关注，其主要用于解决复杂外形网格生成困难和动边界问题［1-2］。作为一种不要求边界和网格重合的方法，IBM 使用简单的、包含边界的笛卡尔网格进行流场模拟。对于动边界问题，IBM 使控制方程能够在一个固定的网格上得到求解，同时可以解决与网格更新相关的关键问题。

IBM 最初由Peskin［3］在20 世纪70 年代提出，用于模拟心脏中的血液流动。在Peskin 的开创性工作之后，许多科学家为提高IBM 的准确性和效率做出了贡献。Huang 和Tian［4］介绍了IBM的基础知识，并评估了最新的进展。Cui 等［5］提出IBM 可以分为基于流体-结构界面表示的扩散界面法和间断界面法两类。

间断界面IBM 是一种离散力法，与扩散界面IBM 不同，它能精确识别物面边界，避免了界面模糊的情况。其主要特点是区分出边界内部、边界外部、以及边界节点，并采用插值方法计算边界节点的流动参数。间断界面IBM 主要包括单元切割法（Cut-cell Method）［6-7］、虚拟单元法（Ghost-cell Method）［8］、笛卡尔浸入边界法（Car‐tesian Immersed Boundary Method）［5，9］。在这些方法中，单元切割法得到的界面最为清晰，这是因为在单元切割法中，边界面将网格节点划分为固相和液相2 个区域，因此，流体的质量、动量、能量守恒定律都能被严格地执行。然而，在模拟运动物体的过程中，单元切割法的网格节点涉及复杂的重塑过程，这给模拟带来了困难。虚拟单元法需要修改的边界节点位于物体内部，该边界节点称为Ghost-cell，虚拟单元法选择在这些点上重建流场变量。笛卡尔浸入边界法类似于虚拟单元法，与之不同的是，该方法的边界节点位于流场内部，边界节点称为IB 点或边界点，重构这些点处的流动变量并加强边界条件可以保证流场的准确性。

自然界中大部分流动都是湍流，尽管可以使用直接数值模拟（Direct Numerical Simulation，DNS）对湍流进行模拟，但由于该方法需要足够小的空间和时间分辨率，现阶段很难使用DNS 模拟较高雷诺数的湍流流动。一种替代方法是使用湍流模型［10］降低数值模拟对网格和时间步长的要求，以这种近似的方法来描述湍流。湍流模型的使用降低了数值模拟对网格的要求，但对于高雷诺数湍流模拟，在壁面附近仍然需要很高的分辨率。由于IBM 大多采用笛卡尔网格，无法做到像贴体网格那样只在物面法向细化网格，满足高雷诺数湍流模拟在物面附近所需要的高分辨率网格的要求，因此大部分IBM 的研究都停留在层流或者无黏流动［11］。为了降低高雷诺数湍流模拟在物面附近的网格要求，可以在IBM 中引入壁面模型［12］。壁面模型提供了一组以壁面剪应力的形式存在的边界条件，从而允许在近壁区域存在较为粗糙的网格。壁面模型的引入使得IBM 在模拟高雷诺数湍流流动时，能保持本身优点且降低对物面附近网格细化的要求，避免网格细化带来的计算效率下降的问题，这拓展了IBM在高雷诺数湍流中的应用［13］。

近年来，国内对IBM 的研究和应用与日俱增。李旭等［14］对Goldstein 提出的反馈力IBM 进行了新的思考，改进了其对力源项的计算，拓展了该方法的使用范围。胡国暾等［15］使用IBM 求解振荡转子叶片的快速计算模型，从而避免了传统方法中由于需要不断重构贴体网格造成的数值模拟的复杂性。陈浩等［16］发展了基于IBM 思想的虚拟单元重构技术，构造了高保真的非贴体笛卡尔网格边界条件，开展了该技术在小展弦比飞翼布局低速流动问题中的应用研究。唐志共等［17］从IBM 出发，结合虚拟镜像对称方法和曲率修正技术进行黏性物面边界条件的处理，同时发展了多值点问题的处理技术，提出了一种在笛卡尔网格下可有效模拟黏性物面边界条件的方法。

本文根据笛卡尔浸入边界法的思想，将边界节点放置在流场中，通过计算代表物面距离的符号向量场（Signed Distance Field，SDF）来区分出固体节点、流场节点以及边界节点，SDF 的结果也可以用于k-ωSST（Shear Stress Transfer）湍流模型。对于Xu 和Liu［18］提到的由于边界节点与壁面距离不规律导致的壁面剪切力计算不光滑的问题，本文采用壁面距离一致的镜像点（Im‐age Point，IP）计算切应力uτ和湍动能耗散率ω，并通过Knopp 等［19］提出的壁面模型计算出边界节点的切向速度，避免了这个问题。

1 数值方法

1.1 控制方程

非定常不可压Navier-Stokes（N-S）方程为

式中：U为速度矢量；p为压强；ρ为密度；μ为黏度；t为时间。

不可压缩流体的连续性方程为

对式（1）取散度并结合式（2），可以得到压力泊松方程

1.2 雷诺平均N-S 方程

采用雷诺平均N-S 方程（RANS）求解湍流问题，RANS 的思路是将流场变量分解为时均分量和脉动分量，即

将（4）～式（7）式代入式（1）、式（2），可得

由于速度分量u′、v′、w′在相关性中可互换，雷诺应力张量只有6 个独立分量，其中u′，v′，w′分别为速度在x、y、z这3 个方向上的脉动分量。为了封闭方程，需要使用湍流模型计算雷诺应力张量，基于涡黏度法［10］，可以将式（8）转化为

式中：μt为湍流黏度。式（11）与式（1）的唯一区别在于耗散项系数由μ转变为μ+μt。

1.3 湍流模型

选择两方程模型k-ωSST 湍流模型计算μt，k-ωSST 是目前工业界较为流行的湍流模型。湍动能k和湍动能耗散率ω的输运方程以微分形式［20］给出

式中：Pk为Faver 平均湍流应力张量和应变律张量的积；σk、σω、γ、β、β*为模型相关的常数；νt为湍流运动黏度；curl（U）为速度的旋度。由于k-ωSST 模型结合了k-ε和k-ω湍流模型，因此k-ωSST 湍流模型所用常数σk、σω、γ、β，通过k-ε和kω湍流模型所用的常数计算得到，计算方式为

式中：Φ为k-ωSST 模型经验常数；Φ1、Φ2为k-ε模型经验常数。

k-ω模型经验常数为

k-ε模型经验常数为

辅助函数F1表示为

式中：d为与壁面最近的网格单元中心与壁面的距离。

辅助函数F2表示为

模型常数为

1.4 壁面模型

使用的壁面模型是基于壁面和对数层外边缘之间的流动由湍流边界层（Turbulent Bound‐ary Layer，TBL）控制的假设得出，其中，二维TBL 方程为

式中：y为壁面法向方向；u为切向速度；S为非定常、对流及压力梯度项之和。

采用Knopp 等［19］提出的一种与k-ωSST 湍流模型一致性的壁面函数，一致性代表壁面函数的解与TBL 方程指定的外边界的位置无关，壁面函数被描述为

使用Spalding［21］提出的拟合公式来描述FSp

FRei，m使用Reichardt 的壁面定律

式中：κ为模型常数；y为第1 层网格高度；u为切向速度；uτ为壁面切应力；ν为运动黏度；y+、u+为表征近壁面流场信息的无量纲量，计算公式为

联立式（22）～式（27）即可求得壁面切应力uτ。

2 浸入边界法

2.1 边界处理

由于本文采用间断界面IBM，为了实施边界条件，需要对网格节点进行区分。将固体边界内部节点标记为固体点（Solid Points，SP），固体边界外部为流场，在流场中根据与边界的距离划分出需要进行处理的边界点（IB Points，IB），以及不需要特殊处理流场点（Fluid Points，FP）。

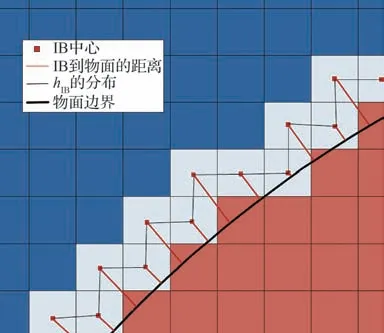
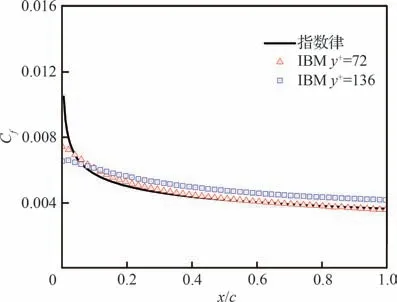
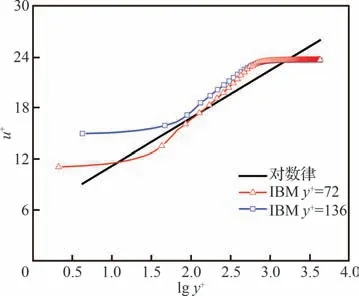
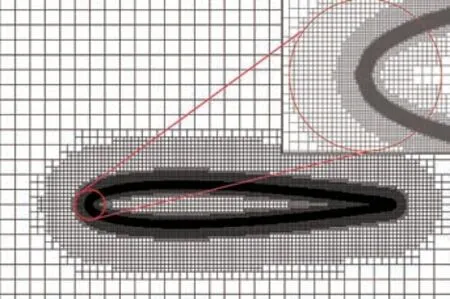
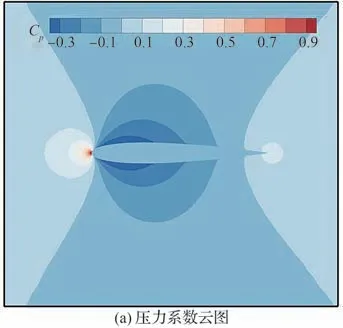
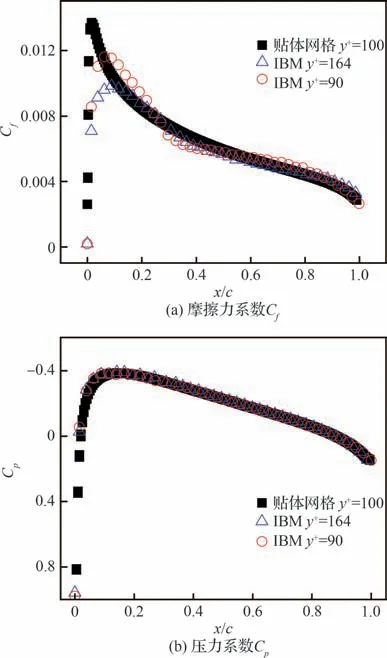
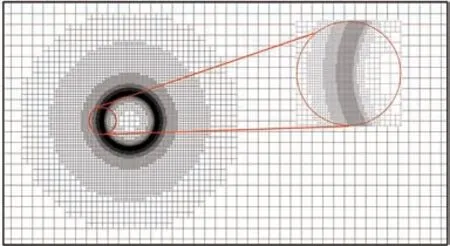
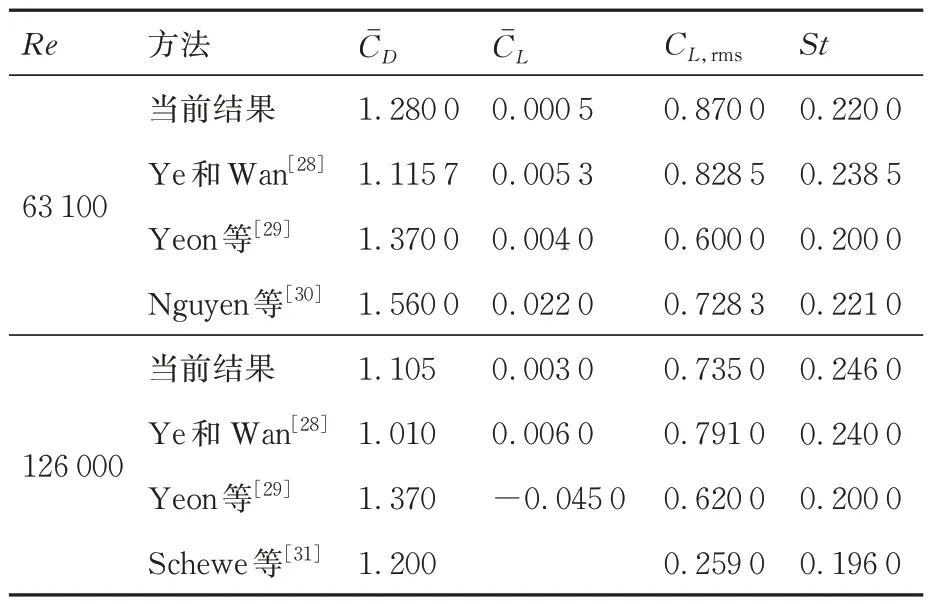
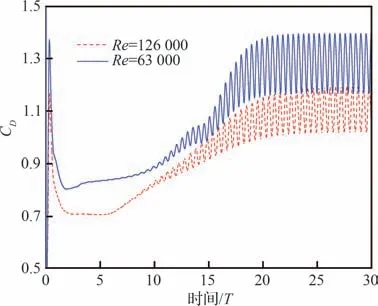
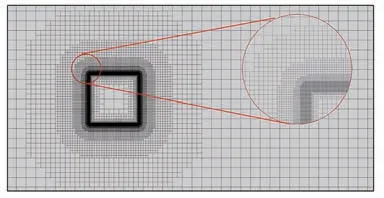
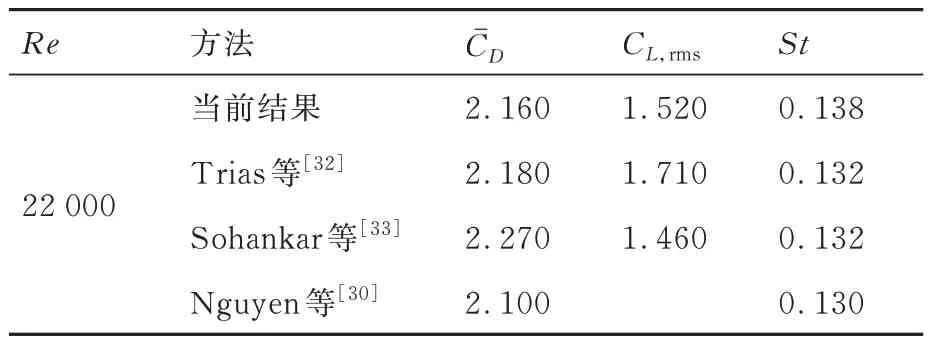
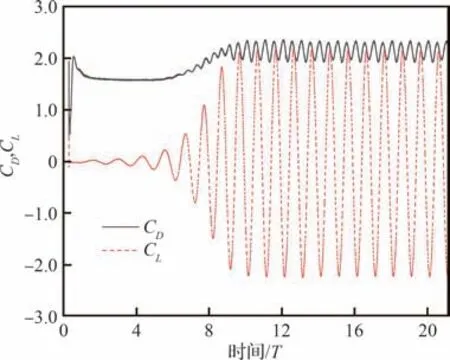
本文根据网格点与壁面的距离计算出SDF，对于SDF ≤0 的点识别为SP（图1 的红色区域），对于0

图1 根据SDF 的单元分区及IP、IB 各点的相对位置Fig.1 Distinguish mesh cell according to SDF and rela‐tive locations of IP and IB points

本文研究发现，h1、h2的选取对模拟结果稍有影响。h1偏小会影响稳定性，h1偏大会影响精度；而h2偏小会导致采样点分布不均，进而影响IP 的计算精度，h2偏大会因为距离IB 距离太远而导致影响IB 的计算精度。因此，对于不同的流动问题需要不同的参数，本文参数的选取标准为

式中：Hmin为最小网格单元长度。本研究均采用直角网格。

2.2 IB 修正

P、B、W点的位置如图1 所示，使用反距离加权插值算法，使用已知的流场变量计算出P点处流场变量的值

式中：R为以P点为圆心的插值模板的半径，本文取R=2Hmin；ri为插值模板中插值点与P点的距离；ϕi为插值点的流场变量。

B点的法向速度UB，normal可以通过P点和W点法向速度线性插值求得

式中：下标normal、tangential 分别表示法向、切向分量；UP为P点速度，由式（29）计算得到；UW，normal为给定的Dirichlet 边界条件的法向分量，hB为B点到壁面的距离。

若物面附近网格足够密，即y+≤1，那么B点的切向速度可以认为同法向速度一样呈线性分布。为了减少对网格的需求，本文使用壁面函数计算切向速度，计算流程如下：

1）根据P点的切向速度计算出壁面切应力uτ，详细的计算流程可参见文献［22］。

2）根据（1）得到的uτ计算出B点处的。

4）由式（27）可得B点的切向速度UB，tangential。

B点的压强可由给定的Neumann 边界条件和P点的压强求得，计算公式为

式中：pB、pP分别为B、P点处的压强。给定0，所以式（31）可简化为pB=pP。式（30）、式（31）对于Dirichlet 和Neumann 边界条件其他流场变量的修改也是通用的。

由于本文使用的是k-ωSST 湍流模型，还需要确定IB 处湍流变量的值。Kalitzin 等［23］给出了黏性层和对数层中k-ω湍流模型的近似解

式中：β=0.075；κ=0.41；Cμ=0.09；y为壁面距离。通常来讲，位于过渡层的ω通过插值近似，本文采用Knopp 等［19］提出的方法计算

采用如下混合公式和渐近关系

使用式（32）～式（34）计算IB 的湍动能耗散率ωIB时，令y=h2而不是直接使用IB 的壁面距离hIB。如图2 所示，一般情况下IB 与壁面的距离hIB不是平滑变化的，这会导致相邻的IB 计算出的ωIB相差较大，从而在一定程度上导致计算难以收敛。

图2 壁面附近hIB的分布情况Fig.2 Distribution of hIB near the wall

对于零压力梯度边界条件，式（21）中的S近似为0，可得式（35），无量纲化得到式（36）。式（37）为Spalding 提出的y+与u+的拟合公式［20］，将式（37）代入式（36）可得IB 的μt。

由μ、ω可得IB 的湍动能k［19］值为

2.3 数值模拟流程

综上所述，当前算法从时间步n到n+1 的求解过程如下：

1）通过式（29）计算出IP 处的速度U和压强p。

2）通过式（30）～式（34）计算IB 处的U和p，并代入控制方程离散矩阵。

3）通过OpenFOAM 求解流场控制方程离散矩阵。

4）重复步骤1～3，直到U和p收敛。

5）计算IB 点的湍流变量ω、k、μt，作为求解k-ωSST 湍流模型的边界条件，并代入湍流模型离散矩阵。

6）通过OpenFOAM 求解k-ωSST 湍流模型。

3 数值算例

3.1 平板绕流

由于湍流平板边界层具有理论上的近似解，可以用来验证求解器解析近壁面流动的准确性。采用近壁面网格密度不同的2 套网格，分别模拟雷诺数Re=1×106，7×105情况下的二维平板湍流边界层问题，并与理论近似解进行对比。网格的y+基于IP 与物面距离计算，即y+=h2uτ/ν。

结果表明，随着y+的减少，表面摩擦力系数Cf逐渐贴近理论值。在Re=1×106、y+=72 时，Cf的数值模拟结果和理论值基本一致。Cf的理论值采用幂律公式计算

式中：x为到平板前缘的距离；c为平板长度；u∞为远前方来流速度。

由图3 可以看出，除了平板前缘附近稍有偏差之外，其他位置的表面摩擦力均与理论值吻合。前缘的误差也出现在其他的模拟中，例如Kalitizin 和Iaccarino［24］、Lee 和Ruffin［25］、Pu 和Zhu［11］等的模拟分析，这可能是因为前缘流场变化剧烈，网格分辨率不足以解析前缘流动导致的。

图3 Re=1×106时使用不同y+网格得到的Cf与理论值对比Fig.3 Comparison of Cf between simulated and theoreti‐cal values using different y+ mesh at Re=1×106

图4 展示了Re=7×105时平板表面Cf分布，它与幂律公式的计算结果基本一致，体现了本文方法对于一定雷诺数范围的湍流平板问题的模拟较为准确。

图4 Re=7×105时的Cf与理论值对比Fig.4 Comparison of Cf between simulated and theoreti‐cal values at Re=7×105

图5 展示了距离前缘x/c=0.9 处x方向的速度型，可以看出基本复合对数律。对数律公式为

图5 Re=1×106时在x/c=0.9 处的速度型Fig.5 Velocity profiles at position of x/c=0.9 for Re=1×106

3.2 NACA0012 翼型绕流

为了验证本文方法的鲁棒性，模拟一个不规则物体的绕流问题。选用NACA0012翼型，自由来流雷诺数Re=1×106，攻角α=0°，计算域为20cairfoil×20cairfoil，其中cairfoil为翼型弦长（见图6）。采用网格密度不同的2 套网格，网格最小尺寸分别是3.8×10−4cairfoil、7.6×10−4cairfoil。这里采用Nguyen等［24］发展的二维网格加密方法对壁面附近的区域进行加密，以确保在整体网格量没有明显增加的前提下使得壁面附近的网格加密，以达到较小的y+值。

图6 NACA0012 翼型周围网格Fig.6 Grid around NACA0012 airfoil

速度、压力系数Cp云图如图7 所示，在攻角为0°的情况下，压强和速度呈对称分布，在翼型前缘可以看到明显的加速，而在1/4 翼型弦长之后速度变化逐渐不明显，对应Cf在翼型表面的分布。压强除了在翼型前端和末端为正值，上下表面附近的压强都为负值。

图7 Re=1×106、α=0°时的压力系数云图及无量纲化的x 方向速度云图Fig.7 Pressure coefficient contour and dimensionless x-direction velocity contour according to inlet ve‐locity for Re=1×106 and α=0°

图8 展示了Re=1×106、α=0°时，2 套不同y+网格下用IBM 模拟得到的Cp、Cf在翼型的表面分布情况，以及与贴体网格的结果对比。可以看到，IBM 的Cp与贴体网格的结果几乎完全吻合。而Cf在前缘附近的结果有些许偏差，这可能是由于前缘流场变化剧烈，现有网格密度不足以完全解析流动导致的数值模拟误差，而本算例只在物体附近加密而非全局网格加密，对数值模拟结果的准确性也会造成一定影响。对比2 套不同网格得到的Cf，可以看出前缘偏差随着网格的加密而减小，证明本方法模拟不规则物体绕流问题的准确性。

图8 表面摩擦力系数和压力系数Fig.8 Skin friction coefficient and pressure coefficient

3.3 Buice 二维扩散管

为了验证本文方法求解分离流问题的有效性，模拟了一个二维非对称扩散器流动问题，外形为美国航空航天局（NASA）提供的模型［26］。根据入口高度和速度计算出的雷诺数为Re=2×104，入口高度H=1 m，入口速度大小Uin=0.2 m/s。

不同位置的水平速度分布与实验数据［27］和贴体网格结果对比如图9 所示，图中的y坐标根据入口高度无量纲化，x坐标根据入口速度和剖面位置无量纲化。IBM 使用了y+=63，112 这2 套不同网格，可以看出得到的数值模拟结果和实验以及贴体网格结果基本一致。y+=112 时得到的分离点较为靠后；随着网格加密，y+=63 时的分离点位置和分离区尺寸与实验结果、贴体网格计算结果基本一致。图10 展示了y+=63 使用入口速度无量纲的速度云图及流线图，其中上半部分是IBM 的结果，下半部分是贴体网格的结果，可以看出两者基本一致。

图9 不同位置的水平速度分布Fig.9 Horizontal velocity profiles at different locations

图10 速度云图和流线图Fig.10 Velocity contours and streamlines

3.4 二维圆柱绕流

圆柱绕流问题一直是测试求解器精度的标准算例，因此本小节模拟了二维圆柱绕流问题。其中，圆柱直径d=1 m，基于圆柱直径的雷诺数分别为Re=63 100，126 000，计算域45d×30d，速度入口条件为均匀来流，压力入口条件为零梯度，速度出口条件为零梯度边界条件，压力出口给定值设置为0，上下边界设置为自由流边界条件。网格单元最小尺寸为0.003d。由于本节主要关注圆柱的受力情况，为了节省计算资源，只对圆柱附近的网格进行加密，网格如图11 所示。

图11 圆柱绕流计算网格Fig.11 Computational grid for cylinder

图12、13 展示了在Re=63 100，126 000 下圆柱绕流的阻力系数CD和升力系数CL随时间变化的曲线，表1 为平均阻力系数、平均升力系数、升力系数均方根CL，rms、斯特劳哈尔数St实验值和数值模拟结果［28-31］对比。可以看出，本文的数值模拟结果与文献结果基本一致。但是，与Yeon 等［29］使用LES 得到的结果对比，CL、St稍大，这可能是由于LES 和RANS 对湍流模化策略不同，以及本文只对近壁面附近的网格加密而没有对尾流区加密导致误差产生。CD、CL、St的计算公式为

表1 圆柱绕流Re=63 100，126 000 时的、CL，rms、StTable 1 ，CL，rms and St for flow around cylinder at Re=63 100，126 000

图12 圆柱绕流CD随时间变化曲线Fig.12 Time histories of drag coefficients of flow around cylinder

图13 圆柱绕流CL随时间变化曲线Fig.13 Time histories of lift coefficients of flow around cylinder

式中：D、L分别为圆柱的阻力、升力；U为给定的入口来流速度大小；fs为涡脱落频率，周期T=1/fs。

图14 给出了Re=126 000 时的无量纲速度、无量纲涡量和压强系数云图，其中速度云图用入口速度无量纲化，涡量用入口速度Uin与圆柱直径d无量纲化，即Wzd/Uin，其中Wz为z方向的涡量。IBM 的结果与文献［30］的结果吻合较好，证明了本文的IBM 可以很好地捕获临界流状态下重要的全局流特征。图15 用流线展示了Re=126 000 时涡在圆柱表面产生、发展、壮大、脱落的全过程。

图14 Re=126 000 时圆柱绕流计算结果Fig.14 Calculation results of flow around a cylinder at Re=126 000

3.5 二维方柱绕流

为了进一步测试本求解器求解钝体绕流问题的精度，模拟了二维方柱的绕流问题。方柱切面为一正方形，边长d=1 m，基于边长的雷诺数为Re=22 000，计算域大小为45d×30d，速度入口条件为均匀来流，压力入口条件为零梯度，速度出口条件为零梯度边界条件，压力出口给定值设置为0，上下边界设置为自由流边界条件。网格单元最小尺寸为0.006d。与3.5 节类似，这里也只对方柱附近的网格进行加密，网格如图16 所示。

图16 方柱绕流计算网格Fig.16 Computational grid for square cylinder

图17 展示了方柱绕流CD、CL随时间变化的曲线，表2 为用本文方法计算得到的平均阻力系数、升力系数均方根CL，rms、施特鲁哈尔数St与其他实验和数值模拟结果［32-34］的对比，可以看到结果基本一致。图18 给出了无量纲化的速度、无量纲涡量和压力系数云图，以及对应时刻的流线图，其中速度云图用入口速度Uin无量纲化，涡量用入口速度与圆柱直径d无量纲化。可以看出本文的方法能很好地捕捉到壁面附近及尾涡的流场细节。

表2 方柱绕流的、CL，rms、StTable 2 ，CL，rms and St for flow around square cylinder

图17 方柱绕流CD、CL随时间变化曲线Fig.17 Time histories of drag and lift coefficients of flow around square cylinder

图18 Re=22 000 时方柱绕流计算结果Fig.18 Calculation results of flow around square cylin‐der at Re=22 000

4 结论

提出了一种可用于模拟不可压黏性流动的间断界面浸入边界法，并将该方法植入开源软件OpenFOAM 中，该方法采用k-ωSST 湍流模型和壁面函数技术降低了湍流模拟时的网格分辨率和时间分辨率要求，为了解决浸入边界法实施壁面函数时出现的物面距离变化剧烈问题，本文采用了IP 与物面的距离参与计算，这有利于减少因为IB 分布变化剧烈导致的壁面附近ω分布变化剧烈的情况，从而提高计算的稳定性。

在应用本文方法时，IB 层的厚度h1、IP 与壁面的距离h2的选取对数值模拟结果稍有影响，选取的值太小不利于计算的稳定性，太大会影响精度。这里给出的参考值是h1=1.5Hmin，h2=3Hmin，对于h1、h2如何影响数值模拟结果还要进一步研究。

为了验证提出方法的有效性，本文进行了相关问题的数值模拟，包括高雷诺数湍流平板绕流、NACA0012 表面压强和切应力分布、Buice 非对称扩散管、圆柱绕流和方柱绕流。计算结果与文献结果相比有较好的一致性，从而验证了本文方法模拟湍流流动的有效性和准确性。未来工作可以在本文方法的基础上，进一步拓展到高雷诺数可压缩流动。