考虑混合润滑的飞机燃油泵径向滑动轴承静特性分析

2023-07-28彭梦丽裴世源林承伟李述林周雅伦葛文兴

润滑与密封 2023年7期

彭梦丽裴世源林承伟李述林周雅伦葛文兴

(1.中国航空工业集团公司金城南京机电液压工程研究中心江苏南京 211100；2.西安交通大学现代设计与转子轴承系统教育部重点实验室陕西西安 710049；3.空军装备部驻上海地区军事代表局驻南京地区第三军事代表室江苏南京 211100)

燃油泵是飞机燃油系统的“心脏”，而轴承是燃油泵的“关节”，是整个燃油泵机械结构的薄弱部件[1]，对其可靠性、经济性、振动特性、稳定性和可维护性具有决定性影响[2-3]。目前，燃油泵的转子普遍采用动压滑动轴承作为支承，同时为了避免额外的供油系统，轴承润滑介质与燃油泵的输送介质相同，为低黏度的RP-3燃油[4]。RP-3燃油动力黏度在0～100 ℃条件下是常见润滑油VG32黏度的1/100～1/10，与水的黏度相当甚至更低，故其油膜承载力差[5-6]，造成轴承的起飞转速高、易磨损，进而造成燃油泵整机寿命低、可靠性差等一系列问题。

自20世纪80年代以来，很多学者在动压轴承的润滑理论方面开展了很多有意义的研究工作。在航空滑动轴承设计领域，AKBARZADEH[7]建立了稳定载荷影响下滑动轴承的热流体力学数值计算模型，分析了垫片数、轴向位置和转速等对轴承性能的影响。符江锋等[5]研究了齿轮式发动机燃油泵滑动轴承间隙比、偏心率、宽径比对滑动轴承润滑静态特性的影响。在轴承润滑计算领域，电解槽模拟法[8]、有限差分法[9]、有限元法[10]均可用于求解Reynolds方程。刘剑和张卫正[11]采用有限体积法计算了内燃机滑动轴承转速、油孔位置、供油压力以及穴蚀对轴承性能的影响。唐云冰等[12]采用有限元分析方法分析了载荷参数对滚动轴承载荷分布影响。史冬岩等[13]采用有限差分法求解了轴承油膜压力分布的情况。郑铁生和许庆余[14]应用有限元法并通过 Newton 迭代求出轴颈平衡位置，同时求得滑动轴承动力特性系数。在低黏度润滑介质润滑方面，朱嘉兴等[15]基于RP-3号燃油建立了燃油齿轮泵滑动轴承的瞬态计算模型，研究了轴承在交变载荷扰动下的瞬态润滑行为。古乐等人[16]通过建立发动机轴承点接触部分膜弹流模型并计算了油膜厚度、油膜压力及粗糙接触压力的分布，分析了低黏度 JP-10 燃油的自润滑性能。JIN和YUAN[17]提出了一种考虑湍流效应的动压轴承力分析方法，导出了适用于低黏度情况下流体动压轴承力的解析表达式。WARRENS等[18]通过实验研究了具有不同黏度的润滑剂及不同调节剂、添加剂等配方的润滑剂润滑下汽车发动机主轴轴承的摩擦性能和承载能力。李威峰[19]采用数值模拟和实验方法测试与分析了高速轴承基于低黏度 RP-3 燃油的油气润滑规律。

虽然已有学者对航空发动机燃油泵等液体润滑轴承开展了理论和实验研究，但二者的轴承类型、工况参数、关键设计变量等均具有明显不同，关于飞机燃油泵动压轴承的设计与原理研究鲜有报道。目前飞机燃油泵动压轴承依然存在以下问题：(a)主要通过查标准和依赖经验设计轴承结构，关键几何参数尚不明确，设计方法尚不成熟；(b)飞机起降及机动过程轴承载荷幅值和方向变化很大，由于燃油黏度极低，油膜形成难，对其安全运行边界尚不清晰。

本文作者在考虑紊流和温升影响的情况下，建立飞机燃油泵用径向滑动轴承的四油叶固定瓦有限元模型，并分析轴承间隙、轴承宽径比、进油温度、转速、径向力和载荷角等关键设计要素对径向滑动轴承静特性的影响规律。

1 理论分析

1.1 物理模型

径向滑动轴承为圆柱环结构，如图1所示。其内表面在圆周方向上均匀分布4个油槽，物理模型可简化为四等分同心圆弧。内圆为轴颈外表面，外圆弧为轴承内表面，中间部分为轴承间隙。

图1 径向滑动轴承结构

1.2 控制方程

考虑到飞机燃油泵径向轴承可能存在的混合润滑状态，首先建立轴承流体域的数学模型，进行瞬态热弹流润滑特性分析[13-14]，基于瞬态雷诺方程、瞬态能量方程、膜厚方程等控制条件，确定方程的边界条件[19-21]及空化效应[22]。采用紊流、质量守恒的流体在微小间隙的运动状态可描述为如下雷诺方程[23-24]：

式中：x=Rθ，R为轴承半径；θ为周向角度；y为轴向坐标；η为润滑油黏度；ρ为润滑油密度；p为油膜压力；Gx和Gy分别是周向和轴向的紊流修正因子，由式(2)和(3)计算，其中Re表示当地雷诺数，由式(4)计算；h为油膜厚度，由式(5)计算；c是瓦块半径间隙；eh和ev分别为轴颈水平和竖直方向的位移。

h=c-ehcosθ-evsinθ

(5)

考虑到混合润滑状态下，轴承的支撑形式将由单纯的流体动静压效应转化为接触载荷与油膜承载的混合模式。因此采用粗糙峰接触模型对混合润滑状态下的雷诺方程进行修正，进而评估接触摩擦的影响。粗糙峰接触的CW模型[25]为

Γ=0.031 54γ-0.031 5χp1(Sk+1)-0.081 6K-0.204 9Mp2Lp3

(6)

式中：Γ为平均表面间隙；K表示峭度；Sk为偏度；M为弹性模量与屈服强度的比值；L为量纲一平均压力；γ为长度比。相应参数详细推导过程见文献[25]。p1、p2、p3为对应系数，取值如下：

p1=0.144 3-0.028 3lnχ

p2=0.877 2-0.064 5lnM

p3=-0.769 1-0.193 8ln(Sk+1)-0.099 4lnK-

0.020 8lnLln(Sk+1)-0.199 4lnL-0.016 6(lnL)2

粗糙峰接触模型综合考虑了局部界面的弹塑性变形、粗糙峰均方根、偏度、峭度等参数对接触压力的影响。考虑粗糙度效应后可以建立平均流模型，动态、层流、可压缩、等温的平均流模型为

在考虑粗糙度效应的求解过程中，理论模型需满足接触承载力与动静压承载力所代表的总承载力与外力相等，因此需要对最小油膜厚度进行反复迭代，直至总体误差达到精度求解即为收敛。

考虑到润滑介质的温黏效应，流体的热效应无法忽略，故采用绝热模型平衡计算时间与精度，能量方程[23]如式(8)所示。

式中：T为沿油膜厚度方向的平均温度；cp为润滑油的比热容；k为润滑油的热传导系数；qx和qy分别为计算域各点周向和轴向的体积流量，分别由式(9)和式(10)计算；τ为作用在轴颈上的切向应力，由式(11)计算，其中Cf为由于紊流所造成的切向应力修正因子，由式(12)计算；U为轴颈线速度。

Cf=1+0.001 2Re0.94

(12)

油膜在水平和垂直方向的承载力即为油膜压力的整体作用，通过对整体油膜压力进行积分即可确定，式(13)给出了对应公式。

式中：B为轴承轴向宽度；L为对应计算域的周向角度。

瓦块两侧的流量由式(14)计算，上下游的流量由式(15)和(16)计算，摩擦力由式(17)计算，功耗由式(18)计算，扭矩由式(19)计算。

(14)

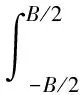
(15)

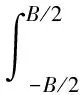
(16)

P=FtU

(18)

Tt=FtR

(19)

基于上述理论模型，燃油泵滑动轴承的各项性能参数均可进行表征。

1.3 边界条件

对于混合润滑的燃油泵轴承，其边界条件主要包括两部分：润滑边界与接触边界。其中润滑边界主要包含雷诺方程及能量方程，雷诺方程的压力边界，以单块瓦为例，考虑到瓦块上下游均为供油槽，即压力为供油压力，不同瓦块边界应当是完全相同的。瓦块两侧的压力设置为0，即为卸油口。能量方程的求解边界即为热边界，文中采用热量守恒方法计算瓦块入口边的温度。接触边界以前文所引述的CW粗糙峰接触模型为主，不再赘述。

考虑到润滑介质黏度的可变性，以Walther模型[23]描述润滑油的温黏特性。由式(20)和(21)确定，即

η0(T)=ρν0

(20)

loglog(v0+0.7)=A-BlogT

(21)

式中：η0和ν0分别为温度T下的动力黏度和运动黏度；ρ为润滑油密度；系数A和B可根据两点的温度和动力黏度进行求解。

1.4 数值求解

采用有限元方法对雷诺方程和能量方程进行求解[26-27]，并采用9节点二阶等参元对雷诺方程进行离散，因为其相对于4节点双线性等参元在流量计算方面具有更高精度。使用高斯积分计算油膜合力，摩擦力、流量等静特性参数。采用Newton-Raphson算法迭代求解轴颈水平和竖直方向上的偏心距、油膜温度和油膜占空比，迭代精度为10-3，最终压力场、温度场及油膜占空比均达到收敛后，采用小扰动法求解动特性系数，计算流程如图2所示。

图2 仿真计算流程

为验证理论模型的正确性，文中以文献[28]试验数据为例来验证建模方法的正确性。文献中径向滑动轴承的几何参数与工况条件如表1所示。数值计算得到的轴承三维油膜压力分布如图3所示，试验和理论计算得到的轴向中心线展开的周向压力分布如图4所示。

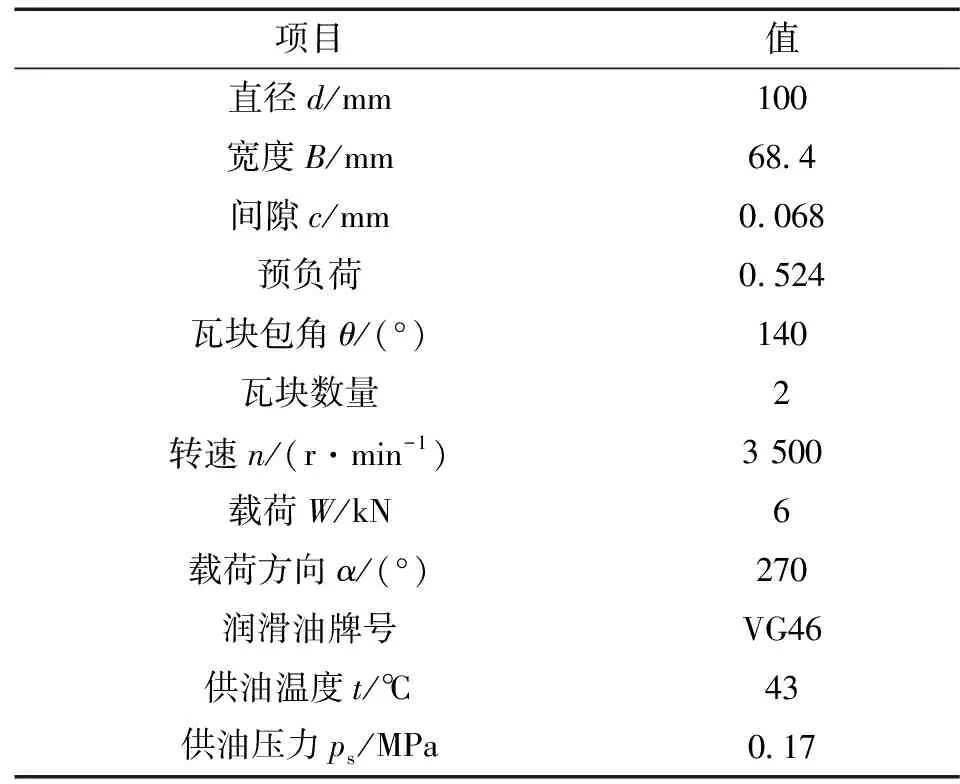
表1 轴承几何与工况参数

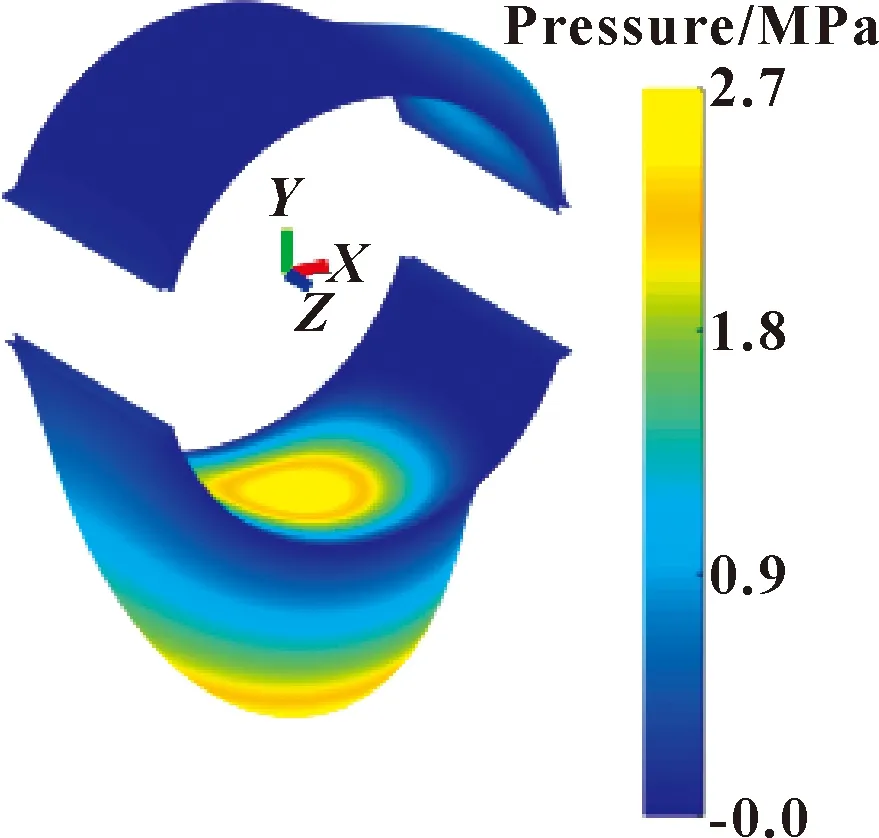
图3 轴承压力分布

图4 轴承圆周方向压力分布

由图3可见，数值计算得到油膜压力分布合理，符合预期。由图4可知，理论及试验得到的压力分布保持一致，在局部位置存在较小的压力误差。总体来说，数值计算结果和试验结果吻合良好，验证了计算程序的正确性。

2 结果与讨论

径向力由螺旋形压水室在运转中产生，由作用在叶轮上的径向力和轴承承载部件的重力叠加得到[3]，典型工况下轴承的主要参数如表2所示。文中径向滑动轴承采用密度为785 kg/m3的RP-3航空燃油润滑，20 ℃下其比热容为2 074.2 J/(kg·℃)，动力黏度为9.7×10-4Pa·s；80 ℃下其比热容为2 307.2 J/(kg·℃)，黏度为3.9×10-4Pa·s。

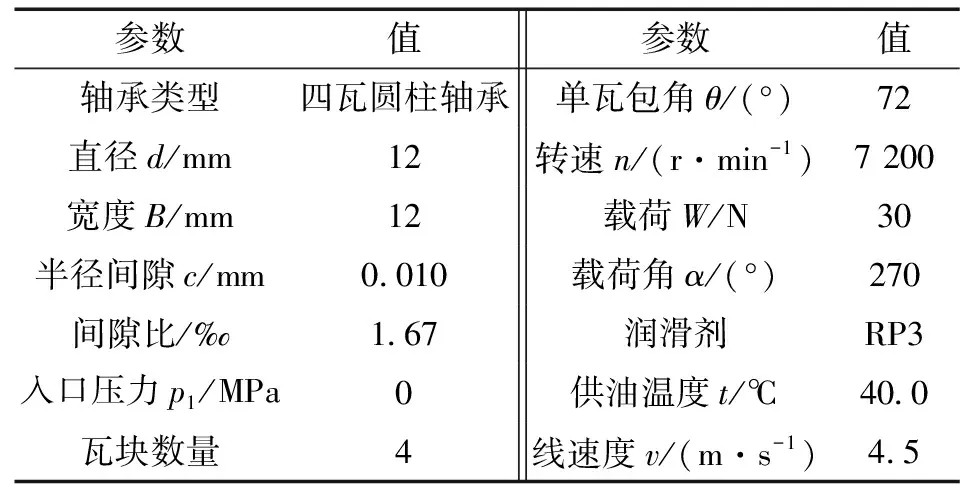
表2 径向滑动轴承主要参数

文中采用控制变量法对轴承间隙、宽径比、进油温度、转速、径向力、载荷角等关键设计因素对轴承静特性的影响规律逐个进行分析，以确定各因素的合理数值。其中轴承的静特性以最小油膜厚度、最大油膜压力、油膜温度及扭矩为主。其中扭矩表示轴承及轴颈间运行阻力矩，当未发生碰摩或粗糙峰接触时，扭矩仅对应于流体的黏性阻力，其值较小；当发生固体接触时阻力会显著上升，因此可以用于判断混合润滑状态下是否发生接触及接触的严重程度。

2.1 间隙对轴承静特性的影响

轴承间隙即轴承的半径间隙比，为滑动轴承最重要的设计参数之一。轴承间隙设计过大，会导致轴承稳定性差，承载力低等缺陷；间隙设计过小也会造成轴承油膜过小，易乏油、抱轴，且加工难度大。文中选取滑动轴承常规设计间隙(5～20 μm)分析轴承间隙对轴承静特性的影响，分析结果如图5所示。

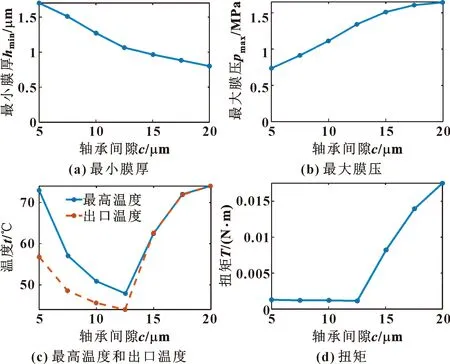
图5 轴承间隙对静特性的影响

图5(a)、(b)显示，随着轴承间隙的增大，最小膜厚逐渐减小，最大膜压逐渐增大，说明轴承理论承载能力逐渐降低。原因在于：间隙增大，导致流体动压效应趋弱，轴承承载能力降低，在外载荷固定的条件下，最小油膜厚度减小、最大油膜压力增大，进而提升承载力达到平衡状态。图5(c)、(d)显示，最高膜温和出口温度、扭矩均在轴承间隙12.5 μm时出现拐点，且参数值均在拐点后逐渐增加，说明轴承间隙大于12.5 μm时，轴承与轴出现明显的接触摩擦。局部的硬性接触导致局部碰摩，进而温度显著上升，扭矩大幅增大。上述分析表明，对于燃油泵径向轴承，为保证轴承稳定润滑，减少碰摩，应控制轴承的半径间隙小于12.5 μm。

2.2 宽径比对轴承静特性的影响

轴承宽径比是滑动轴承重要几何设计参数之一，在轴承内径不变时，宽度增大会导致轴承承载能力上升，但同时会加大供油及冷却难度，引发局部温升过高等异常状态。但宽度过小也会导致承载力不足、油膜过小等不利运行状态。以内径不变，宽径比为0.65～1.35对轴承性能进行分析，结果如图6所示。

以财政部门的预算改革为重点，对资源的分配要真正做到科学合理，要节约资源，对资源做到高效率的利用。对资产分配标准可以分类进行制定，做到详细明确，因为资产标准确定之后，为单位内资产管理和预算管理有机结合和行政事业单位资产的预算都提供了有力的依据。在制定资产分配标准的时候，还要根据实际情况进行具体的分析，行政事业单位之间工作性质的不同，要针对具体的单位运转实际配置相对应的资产，资产分配的多少要根据实际需求和配置标准进行配置，同时还要考虑到随着经济水平的提高，物品价格有所上涨的实际情况，合理分配资产。

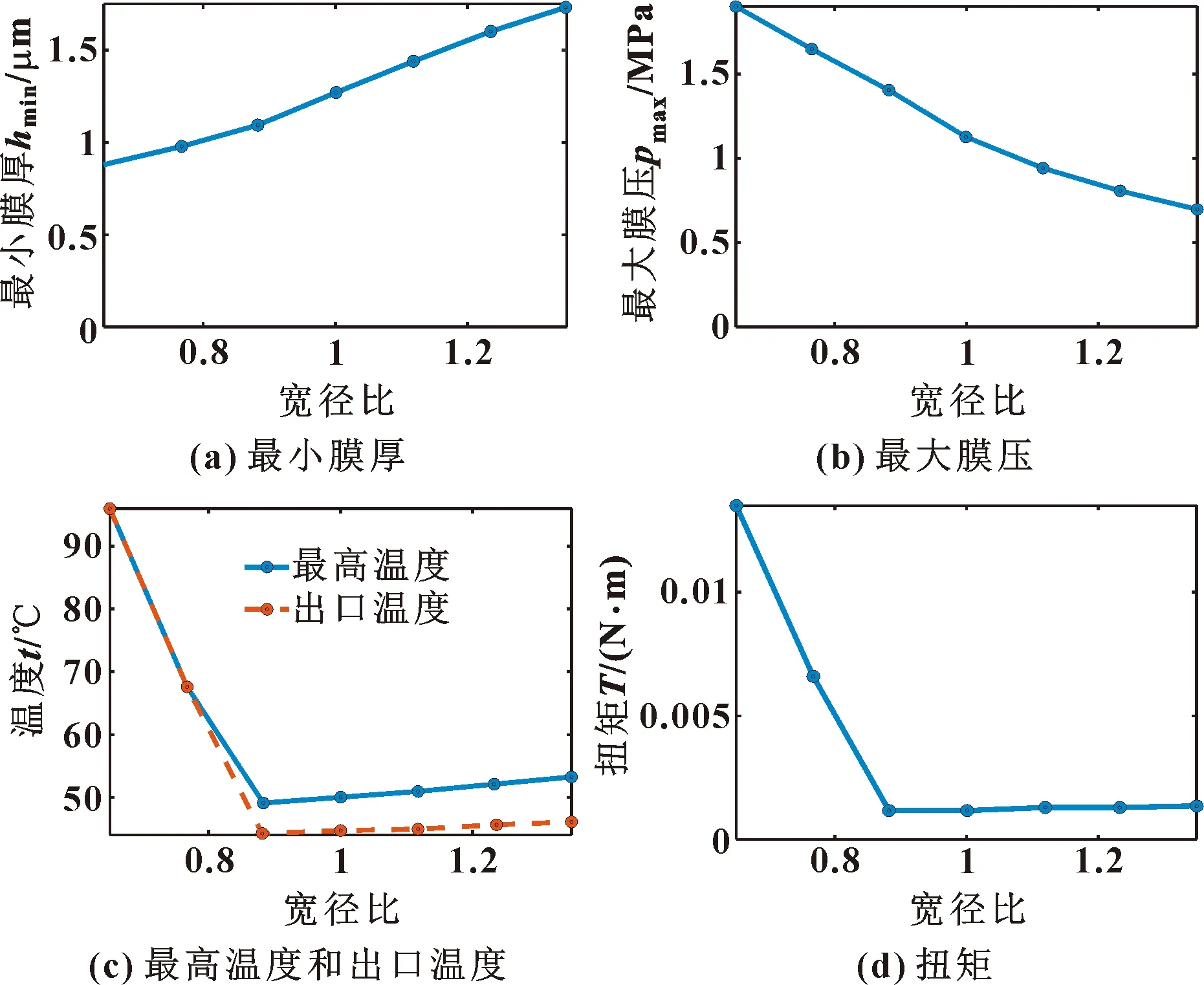
图6 宽径比对静特性的影响

图6(a)、(b)显示，随着轴承宽径比的增大，最小膜厚逐渐增大，最大膜压逐渐减小，轴承理论承载能力逐渐增强。原因即如前述，宽度增加导致承载面积增大，在定载荷工况下，最小膜厚将显著提升，最大压力也会显著降低。图6(c)、(d)显示，最高膜温和出口温度、扭矩均在宽径比为0.89时出现拐点，且参数值均在拐点前逐渐减小，说明当宽径比小于0.89时，轴承承载面积过小，承载力不足，导致油膜厚度过小，进而发生了局部接触摩擦，此时扭矩也会因接触摩擦而显著高于未摩擦阶段。上述分析表明：对于文中所述燃油泵径向轴承工况，应控制轴承的宽径比大于0.89，且应尽可能在空间允许的范围内增大宽径比。文中轴承内径为12 mm，对应的轴承宽度应大于11 mm。

2.3 进油温度对轴承静特性的影响

进油温度主要影响润滑油的黏度变化及系统温升的控制，由于温黏效应的存在，过高进油温度会导致系统温升过大，润滑油黏度过低，影响安全性及承载能力；进油温度过低也会导致润滑油黏度过大，增大系统运行阻力，影响转子运行效率。文中分析了进油温度由30 ℃增大到60 ℃时，对轴承静特性的影响，分析结果如图7所示。

图7 进油温度对静特性的影响

图7(a)、(b)显示，随着进油温度的增大，最小膜厚逐渐减小，最大膜压均逐渐增大。原因在于：根据温黏效应，进油温度越高，润滑油的初始黏度就越小，又根据流体动压效应原理，黏度越小，动压效应的承载力越小，所以最小油膜厚度会降低，最大油膜压力增大，以保证承载力与系统外载荷一致。图中趋势也说明进油温度越低，轴承的承载能力越强。图7(c)显示，进油温度越低，最高膜温和出口温度也越低，油膜的冷却效果越好。图7(d)显示，进油温度在30～55 ℃间变化时，扭矩为略微降低，原因就是流体的黏度降低，而低黏度对应更低的黏性阻力，此时也未发生接触摩擦；当进油温度大于55 ℃后，扭矩大小突增，说明油温过高导致黏度低，承载力差，当黏度小于临界值时，轴承与轴发生明显的接触摩擦，故供油温度的选取应当小于55 ℃。

2.4 转速对轴承静特性的影响

前文分析中均未改变轴承-转子系统的运行边界，旨在优化轴承的设计及运行条件。但轴承的转速、载荷等运行边界也会显著影响轴承的表现性能，文中针对轴承运行转速进行分析，选取转速2 000～9 000 r/min区间，评估轴承的静特性演化特性，结果如图8所示。

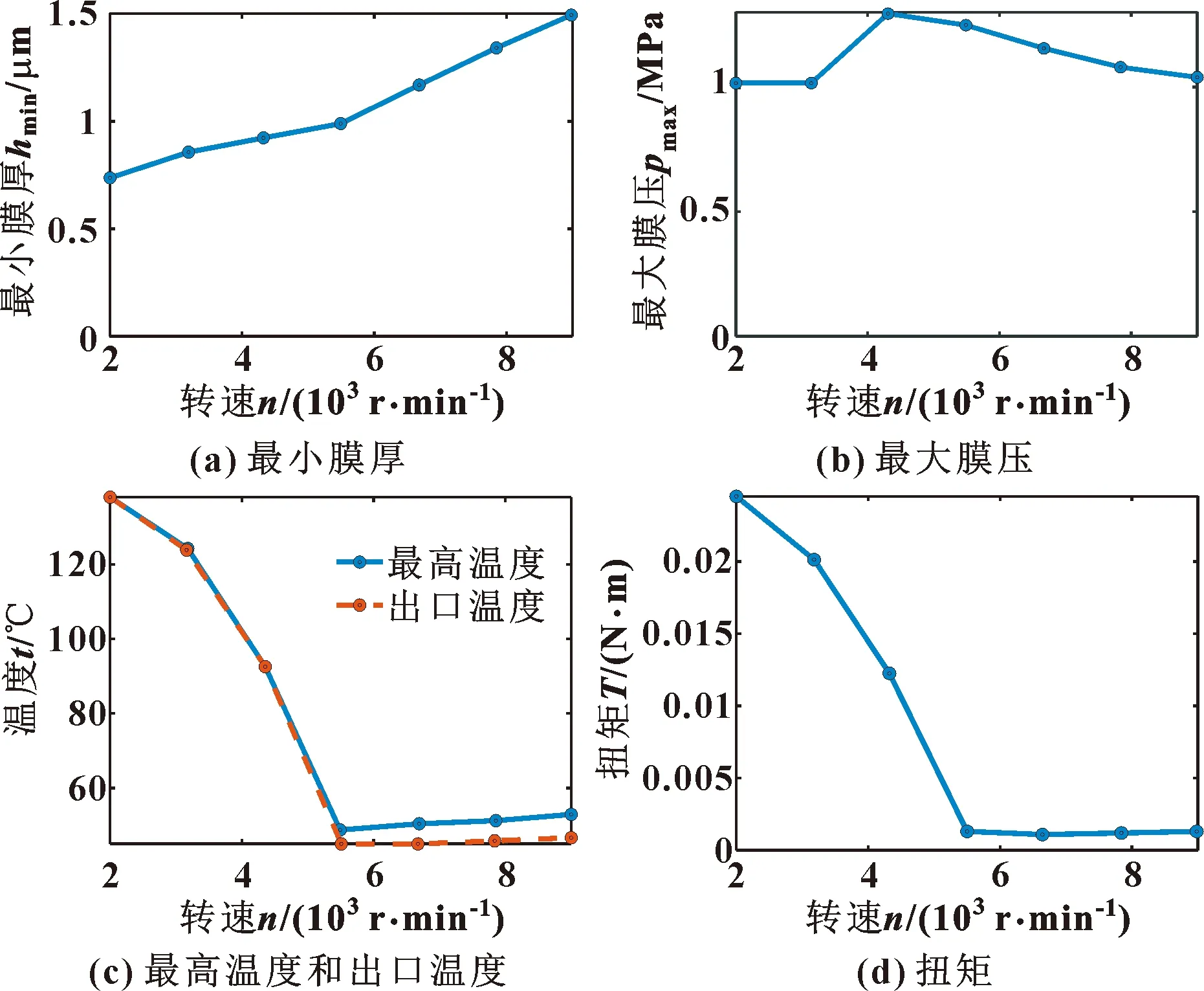
图8 转速对静特性的影响

图8(a)显示，随着转速的增大，最小膜厚逐渐增大，说明轴承承载能力增强。因为界面相对运动速度是影响流体动压效应的关键参数，而转速的升高显著提升了轴颈及轴承界面的相对速度，进而显著提升了流体动压效应，因此轴承承载能力显著上升。图8(b)显示，最大膜压先增大后减小，其变化趋势需结合图8(c)、(d)进行分析。如图8(c)、(d)所示，最高膜温和出口温度、扭矩均在转速为5 500 r/min时出现拐点，且参数值均在拐点前逐渐减小，说明当转速小于5 500 r/min时，轴承与轴出现明显的接触摩擦，最大油膜压力的变化同样是基于该原因。轴承接触摩擦导致局部温升、扭矩增大。同时由于转速在4 000 r/min以下时，接触摩擦严重，固体接触也提供了一部分承载力，所以在同外力载荷下，最大油膜压力会偏小，而当转速在4 000～5 000 r/min时，接触摩擦程度逐渐减轻，此时承载转由油膜压力接手，因此油膜压力会呈现典型的先增大，随后接触摩擦逐渐消失，油膜压力趋于稳定，不再显著变化。上述分析表明，燃油泵径向轴承的理想运行速度应当大于5 500 r/min。

2.5 径向力对轴承静特性的影响

径向力是轴承的主要承载形式，文中分析了径向力由20 N增大到40 N时，对轴承静特性的影响，分析结果如图9所示。

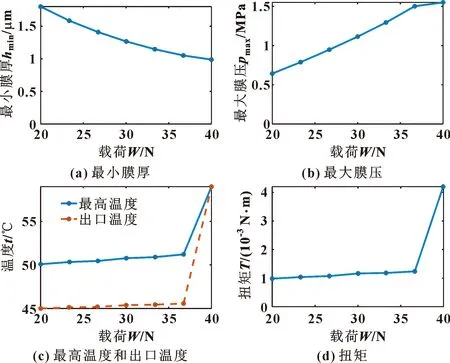
图9 径向力对静特性的影响

图9(a)、(b)显示，随着径向力的增大，最小膜厚逐渐减小，最大膜压逐渐增大，符合轴承载荷增大后最小膜厚及最大膜压的理论变化趋势。图9(c)、(d)显示，最高膜温和出口温度、扭矩均在径向力为36.7 N时出现拐点，且参数值均在拐点后显著增加，说明当径向力大于36.7 N时，轴承与轴出现明显的接触摩擦。当发生接触摩擦后，局部温升会显著提升，且摩擦造成的扭矩显著高于单纯的流体黏性阻力。据此分析，可以认为，该结构参数的轴承，其径向力的承载极限在36.7 N，若要承载更高载荷，则应对轴承参数进行进一步优化。

2.6 载荷角对轴承静特性的影响

考虑到多瓦轴承的供油槽位置及瓦块布置情况，其承载性能与载荷角有着显著联系。文中分析了载荷角由225°增大到315°时，轴承静特性的变化影响，据此可以给出轴承油槽位置及参数的优化方向，分析结果如图10所示。

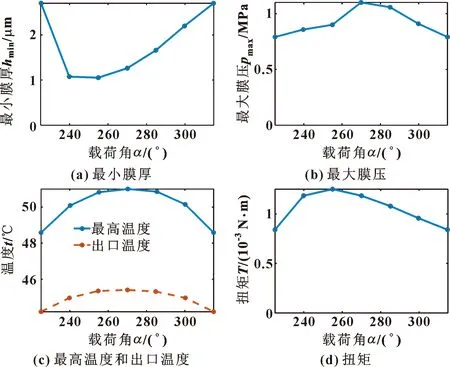
图10 载荷角对静特性的影响

图10(a)、(b)显示，随着载荷角的增大，最小膜厚先减小后增大，最大膜压先增大后减小。结合四瓦轴承的角度关系可知，单瓦72°，则周向261°～279°之间为底部供油槽。随着载荷角的变化，性能会呈现出明显的周期性，225°～315°正好是一个循环区间。当载荷角为225°或315°，载荷方向正好位于瓦块中心，此时承载效果最佳，具有充足的最小膜厚及最大膜压；当载荷角偏离瓦块中心，最小膜厚将降低，最大膜压也将增大，表明承载能力会减弱。图10(c)、(d)显示，最高膜温、出口温度和扭矩同样在一个小的变化范围内先增大后减小，且扭矩在载荷角为255°时的数值最大，轴承与轴摩擦最为明显，此时载荷指向左下方，靠近油槽边界。这是因为油槽会降低轴承的承载能力，油槽边界尤为明显，因此应合理布置轴承的安装方式，尽量将载荷角控制在225°，此时载荷通过瓦片的中心，扭矩最小。同时可以考虑减少油槽的数量，对此需要进一步仿真分析。