不同盆栽基质水分特征曲线的对比分析与模拟

朱钊岑，邵明安,3，赵春雷，贾小旭，王 娇

•农业生物环境与能源工程•

不同盆栽基质水分特征曲线的对比分析与模拟

朱钊岑1,2，邵明安1,2,3，赵春雷1,3※，贾小旭1,3，王 娇1,3

（1. 中国科学院地理科学与资源研究所黄河三角洲现代农业工程实验室，北京 100101；2. 西北农林科技大学资源环境学院，杨凌 712100；3. 中国科学院大学资源与环境学院，北京 100190）

现有关于盆栽控水模拟土壤干旱条件的试验中多采用含水率作为水分胁迫阈值，然而由于基质配比不同导致含水率相同的基质的水分状况也不尽相同，这导致各研究间结果难以对比和参考。为快速获取盆栽基质水分特征曲线，建立基质水分特征曲线预测模型。该研究以盆栽控水试验常用的泥炭土、蛭石和珍珠岩为基质材料，测定了不同配比基质的水分特征曲线，通过不同方法（多元回归模型、人工神经网络）建立了其预测模型。结果表明，人工神经网络模型对泥炭土-蛭石复配基质水分特征曲线的预测精度高于多元回归；相较于人工神经网络，多元回归模型的稳定性更高。综合考虑模型的精度和稳定性，多元回归模型是预测作物盆栽基质水分特征曲线的最佳模型，预测精度2≥0.950，平均误差接近0。该模型为基质水分特征曲线快速获取以及相关作物干旱胁迫研究间的对比提供了方法和依据。

模型；基质；水分胁迫；盆栽试验；水分特征曲线；传递函数

0 引 言

水分胁迫阈值是判断作物水分胁迫响应的重要指标，盆栽人工控水模拟土壤干旱条件，是确定作物水分胁迫阈值的重要方法[1-2]。现有研究中的水分胁迫阈值大多采用含水率指标，对基质水势测定较少。尽管部分研究对基质水势进行了测定，但其仅用于判断补水时机和维持基质水分恒定，并未将其作为水分胁迫指标[3-4]。作物对水分的吸收主要与根系和土壤中水分的能量状态（水势）有关[5]。在不同的盆栽基质中，同一含水率往往对应着不同的水势[6]。这就导致了以含水率形式表达的水分胁迫阈值在不同研究间难以统一，不仅不利于准确认识水分在土壤和根系间的传输过程，还限制了不同研究结果间的对比和参考[7-9]。水分特征曲线反映了基质水分数量和能量之间的关系。利用水分特征曲线，将含水率转换为水势，是解决上述问题的有效方法。

在盆栽控水试验中，泥炭土、蛭石和珍珠岩是当前应用最广泛的基质复配材料[10]。不同基质材料具有相对固定的孔隙分布特征与持水特性，作物盆栽基质在不同水势下的持水量主要取决于复配基质所用的材料及其配比[11-12]。然而，不同研究中的基质配比往往存在差异，导致其盆栽基质水分特征曲线不同[6]。即便少数研究进行了测定，这些水分特征曲线也仅适用于特定基质，不具有通用性[13-14]。传递函数模型是快速获取水分特征曲线的有效方法。在土壤物理学领域，众多学者利用土壤颗粒组成、有机质含量、饱和导水率等参数，成功建立了不同类型、质地土壤的水分特征曲线预测模型[15-17]。相较于土壤，盆栽基质的组成更为简单[10]。若能够建立不同组成和配比的基质的通用水分特征曲线预测模型，则有望获得一条快速获取盆栽基质水分特征曲线的有效途径。

综上，为了建立不同配比基质的水分特征曲线预测模型，实现不同研究间水分胁迫阈值由含水率向水势的转换，本研究采用3种常用的基质复配材料（泥炭土、蛭石和珍珠岩），开展不同配比下的盆栽试验，通过测定不同配比基质的水分特征曲线，分析基质配比与水分特征曲线参数间的关系，最终建立水分特征曲线的预测模型，以期为基质水分特征曲线的快速获取及不同研究间水分胁迫阈值的转换、对比提供方法和依据。

1 材料与方法

1.1 供试材料和试验设计

本研究选取泥炭土、蛭石（粒径<2 mm）和珍珠岩（粒径<2 mm）3种基质材料，根据不同研究中常见的复配比例[7-9]，共设置11个处理。不同处理3种基质材料的体积比详见表1。

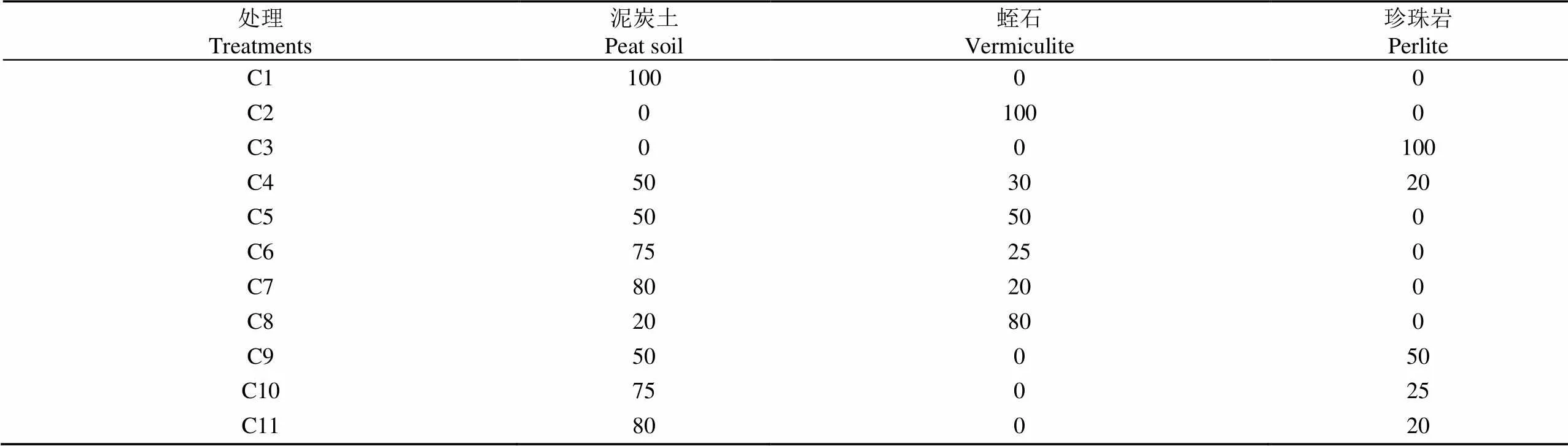
表1 基质材料配比体积比设计

1.2 基质水分特征曲线的测定

将复配好的11种基质分别填入环刀后置于水中浸泡24 h，每个处理3个重复，共计33个样品。样品的水分特征曲线采用利用离心机法测定。将饱和后的土样放到离心机中，通过设置离心机（HITACHI CR21G，日本）的转速以实现不同的水吸力环境，待测试样水分达到平衡后，取出样品并称取其质量。测试结束后，利用烘干法（105 ℃，12 h）测定基质干质量，计算不同水吸力下对应的体积含水率。

1.3 数据处理

1.3.1 水分特征曲线与当量孔径

在众多描述水分特征曲线的模型中，van Genuchten模型（VG模型）是最为常用的水分特征曲线拟合模型，该模型具有广泛的适用性，对于不同介质均具有较高的拟合精度。因此，本研究采用VG模型对不同处理基质实测的水分特征曲线进行拟合，VG模型表达式如下[18]：

式中为基质含水率，cm3/cm3；θ为饱和含水率，cm3/cm3；θ为残余含水率，cm3/cm3；为基质势，kPa；、和为经验参数，为进气值的倒数，cm-1，和为水分特征曲线形态学参数，=1−1/。

基质的持水能力与其孔隙分布特征密切相关，当量孔径与水吸力的关系为[19]：

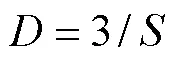
式中为当量孔径，mm；为水吸力，hPa。

根据当量孔径的大小，将基质当量孔径划分为3类：通气孔隙（>9×10-3mm）、毛管孔隙（9×10-3～2×10-4mm）和无效孔隙（<2×10-4mm），分别对应相应的水吸力分别为<33、33～1 500、>1 500 kPa：其中，<33和>1 500 kPa基质水吸力分别对应重力水和无效水，33～1 500 kPa基质水吸力对应毛管水[20]。

1.3.2 水分特征曲线预测模型的建立

本研究拟在11种基质材料水分特征曲线的基础上，利用不同配比基质水分特征曲线的实测数据（水势、含水率），采用数学回归（多元回归模型）和机械学习（人工神经网络）的方法，建立不同配比基质的水势与含水率预测方程。再通过bootstrap方法将不同配比基质的水势与含水率数据随机分为建模数据（80%，108组水势与含水率数据）与验证数据（20%，28组水势与含水率数据），分别用于模型的建立与验证。在建模过程中共进行30次数据随机分组，用于评价模型的预测精度和稳定性。

多元回归指利用线性回归方程定量分析因变量与多个自变量间的关系[21]。在本研究中，多元回归模型的表达式为

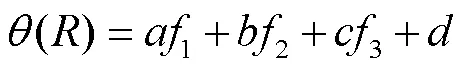
式中(R)为水吸力为时处理基质的体积含水率，cm3/cm3；R为处理中泥炭土、蛭石和珍珠岩的体积百分比；、、为系数，为常数项。1、2和3分别为蛭石、泥炭土和珍珠岩的水分特征曲线。

人工神经网络模型是一种模拟人脑结构和功能，由大量节点相互连接而成的大规模信息处理系统[22-23]。由输入层、隐藏层与输出层三部分组成，其中输入层负责接受外界的信息，并将其作为模型的输入信息传递给隐藏层；隐藏层是模型的内部信息处理层，负责数据处理与转换并将结果传递给输出层，不同隐藏层具有不同的权重；输出层根据隐藏层权重和自身偏置输出模型最终结果。不同层由若干神经元组成，神经元与神经元间的连线为对应权重。对于单个神经元，其输出结果由输入与对应权重的非线性激活函数确定[24]，其表达式为

式中y为神经元的输出，x为神经元的输入，w为对应权重，为神经元的激活阈值。

参照多元回归模型，本研究中人工神经网络模型同样以泥炭土、蛭石和珍珠岩3种材料在水吸力为时VG模型中相应的体积含水率和不同基质材料的配比为自变量，复配基质体积含水率为因变量，最终建立人工神经网络模型。

本研究选取决定系数（2）、归一化均方根误差（NRMSE）和平均误差（MR）对模型预测精度进行评价，其计算式参见文献[25-26]。

2 结果与分析

2.1 3种基质材料水分特征曲线对比

基于不同水吸力下的含水率数据，利用VG模型对3种基质材料（泥炭土、蛭石、珍珠岩）水分特征曲线进行参数拟合（表2）。由表2可知，VG模型可以很好地拟合3种基质材料的水分特征曲线（2≥0.990）。对比3种基质材料的水分特征曲线，3种基质材料的饱和含水率由高到低分别为泥炭土（0.655 cm3/cm3）、蛭石（0.441 cm3/cm3）、珍珠岩（0.440 cm3/cm3）（表2）。在低吸力段（水吸力小于33 kPa），随着水吸力的增加，3种基质材料含水率均快速降低；3种基质水分释放量与饱和含水率之比为48.09%～85.68%。在中高吸力段（水吸力33～800 kPa），随水吸力的增大，泥炭土与珍珠岩含水率变化较小，而蛭石仍有较多的水分释放；泥炭土、珍珠岩水分释放量与饱和含水率比分别为10.04%和5.30%，而蛭石为41.21%（图1）。盆栽基质的释水特性与基质本身的矿物组成与孔隙特征密切相关。蛭石为2：1型矿物，水分子主要填充于层间，部分水分子围绕层间阳离子形成水合络离子，其余呈游离态[27]。随着水吸力的增大，层间水逐渐释放；因此在中高吸力段，蛭石含水率逐渐降低（图1）。泥炭土较为蓬松，有机质含量较高，阳离子较多，存在较多结合水[28]；因此在中高吸力段含水率较高。珍珠岩具有良好的透气性，但持水性较差；水分主要附着于颗粒表面，多为重力水[10]。在释水过程中，随着水吸力的增大，珍珠岩含水率迅速降低；水分释放主要发生在低吸力段。

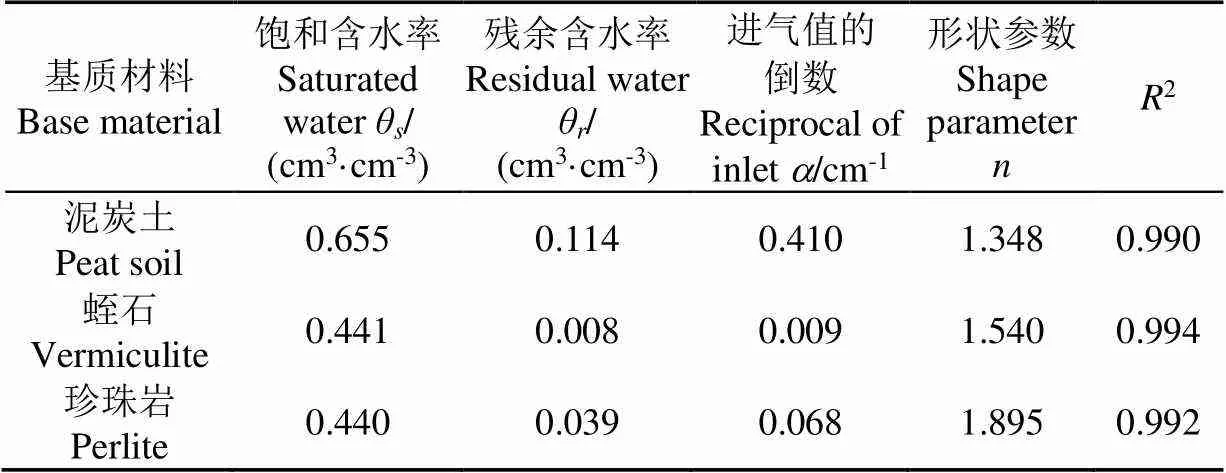
表2 3种基质材料的水分特征曲线参数

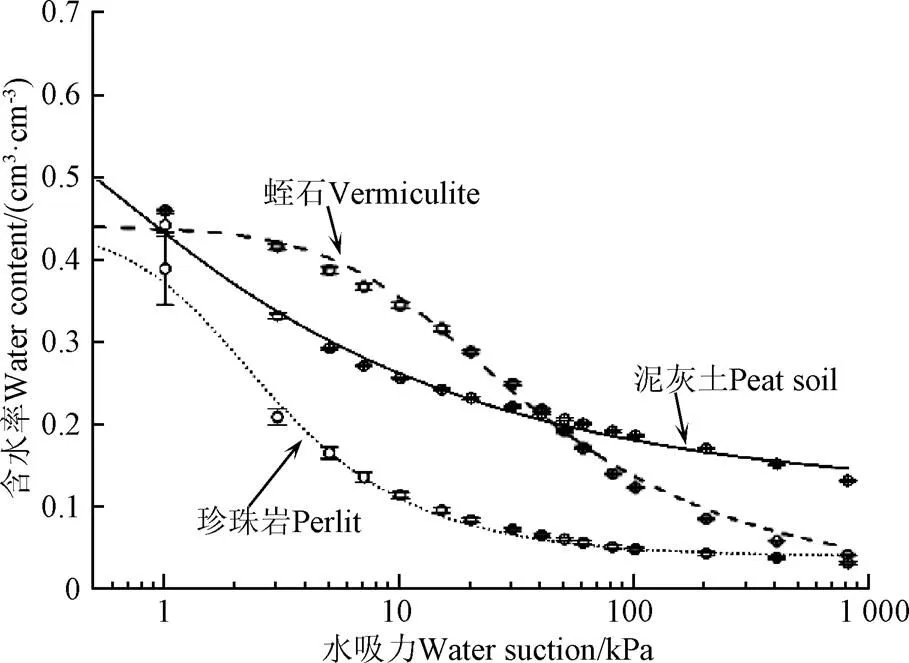
图1 3种基质材料的水分特征曲线

孔隙分布特征与基质水分特征曲线、持水能力密切相关[29]。在水分特征曲线中，低吸力段，水分释放主要发生在通气孔隙中；随着水吸力的增大，水分释放逐渐转变为有效孔隙[6,20]。泥炭土总孔隙度为65.64%，蛭石为44.08%，珍珠岩为44.03%。泥炭土和珍珠岩以>9×10-3mm孔隙为主，分别占其总孔隙的67.83%和85.68%，因此泥炭土和珍珠岩在低吸力段含水率快速降低。而二者2×10-4～9×10-3孔隙较少，分别占总孔隙的10.87%和5.30%，是其在中高吸力段水分特征曲线趋于平缓的主要原因。蛭石以>9×10-3mm和2×10-4～9×10-3mm孔隙为主，分别占其总孔隙的48.09%和43.35%。蛭石2×10-4～9×10-3mm孔隙含量较高是其在中高吸力段含水率随水吸力的增加而降低的主要原因。泥炭土较蛭石和珍珠岩具有更多的<2×10-4mm孔隙，使得泥炭土残余含水率（0.114 cm3/cm3）大于珍珠岩（0.039 cm3/cm3）和蛭石（0.008 cm3/cm3）（图2）。

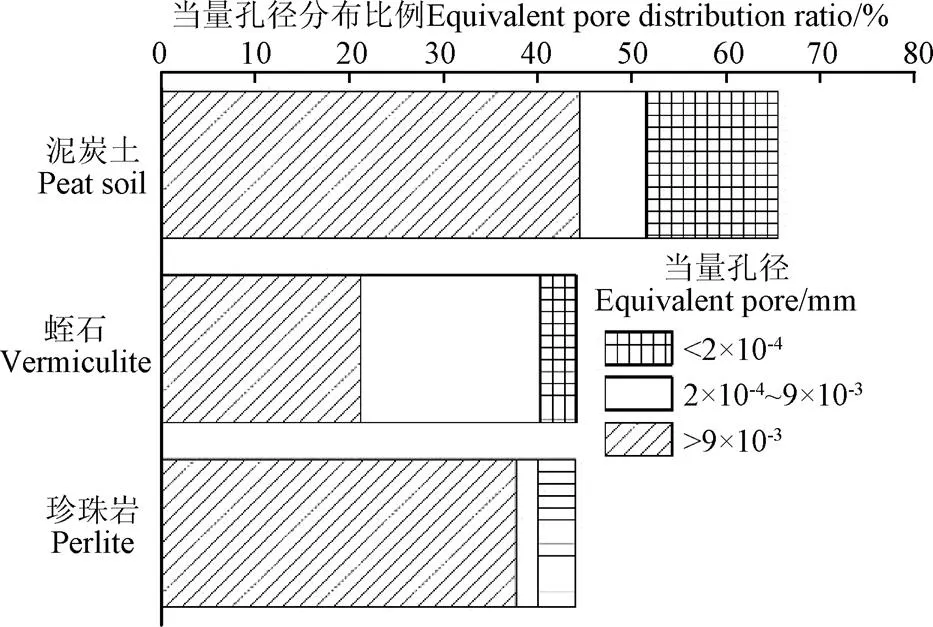
图2 3种基质材料不同当量孔径的孔隙度

2.2 基质水分特征曲线模型的建立与模拟

2.2.1模型构建

基于3种基质的水分特征曲线及不同配比基质在不同水吸力下的含水率，分别利用多元回归和人工神经网络方法建立了不同配比基质水分特征曲线预测模型（图3）。对比不同建模方法水分特征曲线预测值与实测值，不同建模方法间，模型预测精度的差异主要体现在泥炭土-蛭石和泥炭土-珍珠岩2类复配基质。人工神经网络模型对泥炭土-蛭石复配基质水分特征曲线的预测精度优于多元回归模型；对于泥炭土‐珍珠岩复配基质，结果则相反；但二者精度差异不显著（表3）。在不同水吸力条件下，相较于人工神经网络，多元回归模型在5个处理中低估了复配基质的含水率（图3）。这主要是由于多元回归模型低估了复配基质的饱和含水率（表4），进而降低了水分特征曲线初始值[6]。

表3 不同模型对各处理不同水吸力下体积含水率的预测精度

注：NRMSE为归一化均方根误差；MR为平均误差

Note:NRMSEis normalized root mean square error;MRis average error.

在中高吸力段（>33 kPa），人工神经网络低估了C5处理不同水吸力下的含水率，其原因主要是对残余含水率的低估（图3b，表4）。在水分特征曲线中，随着水吸力的增大，基质中通气孔隙中的水分最先释放，其次为有效孔隙，最后为无效孔隙[6]。θ主要受无效孔隙（<2×10-4mm）的影响，进而决定高吸力段水分特征曲线的形状[29]。多元回归模型对C6与C7处理在中吸力段（33～100 kPa）含水率存在明显的高估（图3c和图3d）。对比实测与预测水分特征曲线VG模型参数，发现多元回归模型低估了参数（表4），导致C6和C7处理水分特征曲线在中吸力段较实测更平缓[30]。对于C8处理，多元回归模型对θ的低估是导致其在初始阶段预测值偏低的主要原因（图3e，表4），同时对参数的低估是导致其低吸力段（<33 kPa）预测值偏大的主要原因。

图3 不同处理实测和预测水分特征曲线的对比

表4 水分特征曲线参数实测值与预测值的对比

对于将泥炭土与珍珠岩作为复配材料的处理，多元回归模型对水分特征曲线预测的预测精度要高于人工神经网络模型（图3f～图3h，表3）。在低吸力段（<33 kPa），人工神经网络模型对C10与C11处理含水率存在明显的高估，其原因主要是由于该模型对参数的预测存在较大的误差（图3g，图3h，表4）。在VG模型中，为进气值倒数，反映土壤初始排水时难易程度；越小，代表土壤初始排水越难，水分特征曲线在初始阶段越平缓[31]。

2.2.2 不同建模方法的稳定性分析

模型的最佳精度不是评判模型优劣的唯一标准，还应考虑模型的稳定性[32-34]。模型的精度主要与建模和验证过程所选取的数据集有关。为了消除特定数据集（某一次选取的建模数据与验证数据）对模型精度造成的随机偏差[21]，本研究通过bootstrap方法进行了30次数据随机分组、建模和验证，用以综合评价不同建模方法所建立模型的预测精度和稳定性。结果表明，在30次建模和验证过程中，人工神经网络模型实现的最佳精度要优于多元回归，但其NRMSE、2和MR的方差与分布范围均大于多元回归（图4）。此外，建模和验证过程中多元回归模型的NRMSE的均值小于人工神经网络模型，2的均值大于人工神经网络模型，且MR更接近于0。因此，在本研究中，多元回归建立的预测模型较人工神经网络具有更好的稳定性[21]。此外，人工神经网络为黑箱模型，无法直观解释其中非线性函数的实际物理意义；且随着人工神经网络模型规模的增大，其非线性函数呈指数增加，使得模型更为复杂，不便于使用[35]。相比之下，多元回归模型的表达形式具体且直观，模型的易用性更好[22]。因此，多元回归方法是建立基质水分特征曲线预测模型的最优方法，本研究中基于多元回归方法建立的最优基质水分特征曲线预测模型的表达式为

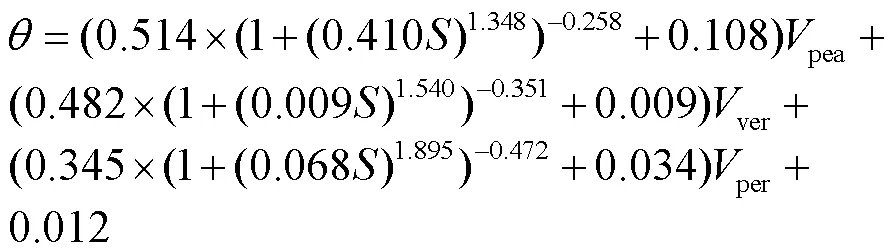
式中θ为水吸力S时的基质体积含水率，cm3/cm3；S为水吸力，cm (1 cm=0.098 kPa)；Vpea、Vver、Vper分别为不同基质中泥炭土、蛭石与珍珠岩的体积百分数，%。

2.3 多元回归模型精度验证

为验证多元回归模型对不同配比基质水分特征曲线的预测精度，本研究重新配置了6种不同配比基质（表5），测定其水分特征曲线，与模型模拟结果（将水和单位换算为kPa）进行对比，结果如图5所示。

由图5可知，多元回归模型对不同配比基质水分特征曲线具有较高的预测精度（2≥0.950，较小的NRMSE，MR接近于0）（图5）。对比不同组合复配基质，多元回归模型对泥炭土‐珍珠岩复配基质较泥炭土‐蛭石具有更高的预测精度。对于泥炭土‐蛭石‐珍珠岩复配基质，多元回归模型对不同水吸力的含水率预测精度存在一定差异，但整体上仍具有较高的预测精度（2>0.950）。可见，基于多元回归方法建立的基质水分特征曲线预测模型具有可靠性。

表5 用于模型验证的基质材料配比体积比

图5 不同处理实测与多元回归模型模拟水分特征曲线的对比

3 结 论

为了快速获取不同研究中盆栽基质的水分特征曲线，本研究以盆栽控水试验常用的泥炭土、蛭石和珍珠岩为基质材料，测定了不同配比基质的水分特征曲线，通过不同方法（多元回归模型、人工神经网络）建立了其预测模型。结果表明：

1）van Genuchten模型对3种基质水分特征曲线均具有较高的拟合精度（2≥0.990）；

2）人工神经网络和多元回归模型对不同配比基质水分特征曲线的预测精度差异不大，但人工神经网络模型在不同配比基质水分特征曲线的预测稳定性低于多元回归模型；

3）综合考虑模型的精度和稳定性，多元回归方法是建立不同配比基质水分特征曲线预测模型的最佳方法，经验证，其精度高于0.9，基于该方法建立的模型为不同配比盆栽基质水分特征曲线的快速获取提供了可靠途径。

[1] 宋松泉，王彦荣. 植物对干旱胁迫的分子反应[J]. 应用生态学报，2002，13(8)：1037-1044.

SONG Shongquan, WANG Yanrong. Molecular response of plant to drought stress[J]. Chinses Journal of Applied Ecology, 2002, 13(8): 1037-1044. (in Chinese with English abstract)

[2] 王卫星，杨明欣，高鹏，等. 基于多光谱和气象参数的菜心水分胁迫指数反演[J]. 农业工程学报，2022，38(6)：157-164.

WANG Weixing, YANG Mingxin, GAO Peng, et al. Inverting the water stress index of theusing multiple-spectral and meteorological parameters[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2022, 38(6): 157-164. (in Chinese with English abstract)

[3] LI G, LIN L, DONG Y Y, et al. Testing two models for the estimation of leaf stomatal conductance in four greenhouse crops cucumber, chrysanthemum, tulip and lilium[J]. Agricultural and Forest Meteorology, 2012, 165: 92-103.

[4] ZHANG N Y, LI G, YU S X, et al. Can the responses of photosynthesis and stomatal conductance to water and nitrogen stress combinations be modeled using a single set of parameters?[J]. Frontiers in Plant Science, 2017, 8: 328.

[5] CAI G C, van DERBORGHT J, COUVREUR V, et al. Parameterization of root water uptake models considering dynamic root distributions and water uptake compensation[J]. Vadose Zone Journal, 2018, 17(1): 160125.

[6] 邵明安，王全九，黄明斌. 土壤物理学[M]. 北京：高等教育出版社，2006.

[7] LAMHAMEDI M S, MARGOLIS H, RENAUD M, et al. Effects of different irrigation intensities on growth, mineral nutrition and nutrient leaching of 1+0 black spruce produced in air-slit containers in a forest nursery[J]. Canadian Journal of Forest Research, 2003, 33(2): 279-291.

[8] CHAMBEL M R, CLIMENT J, ALIA R. Divergence among species and populations of Mediterranean pines in biomass allocation of seedlings grown under two watering regimes[J]. Annals of Forest Science, 2007, 64(1): 87-97.

[9] CARLES S, LAMHAMEDI M S, STOWE D C, et al. Frost tolerance of two-year-oldseedlings grown under different irrigation regimes in a forest nursery[J]. Scandinavian Journal of Forest Research, 2008, 23(2): 137-147.

[10] 朱建龙，张潇丹，颉建明，等. 日光温室栽培基质有效导热系数预测模型[J]. 农业工程学报，2021，37(24)：199-207.

ZHU Jianlong, ZHANG Xiaodan, XIE Jianming, et al. Prediction models for the effective thermal conductivity of cultivation substrates in solar greenhouses[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(24): 199-207. (in Chinese with English abstract)

[11] 张乃于，闫双堆，任倩，等. 珍珠岩粒径对土壤水分运移的影响[J]. 灌溉排水学报，2019，38(2)：22-28.

ZHANG Naiyu, YAN Shuangdui, REN Qian, et al. Water movement in soil amended with perlite particles of different sizes[J]. Journal of Irrigation and Drainage, 2019, 38(2): 22-28. (in Chinese with English abstract)

[12] JOHN A, FUENTES H R, GEORGE F. Characterization of the water retention curves of Everglades wetland soils[J]. Geoderma, 2021, 381: 114724.

[13] 张雅馥，王金满，王敬朋，等. 生物炭添加对矿区压实土壤水力特性的影响[J]. 农业工程学报，2021，37(22)：58-65.

ZHANG Yafu, WANG Jinman, WANG Jingpeng, et al. Effects of biochar addition on the hydraulic properties of compacted soils in mining areas[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(22): 58-65. (in Chinese with English abstract)

[14] 邓羽松，丁树文，蔡崇法，等. 鄂东南崩岗剖面土壤水分特征曲线及模拟[J]. 土壤学报，2016，53(2)：355-364.

DENG Yushong, DING Shuwen, CAI Congfa, et al. Characteristic curves and model analysis of soil moisture in collapse mound profiles in southeast Hubei[J]. Acta Pedologica Sinica, 2016, 53(2): 355-364. (in Chinese with English abstract)

[15] RAM S, PRASAD K S H, GAIROLA A, et al. Estimation of border-strip soil hydraulic parameters[J]. Journal of Irrigation and Drainage Engineering, 2012, 138(6): 493-502.

[16] QIAO J B, ZHU Y J, JIA X X, et al. Development of pedotransfer functions for soil hydraulic properties in the critical zone on the Loess Plateau, China[J]. Hydrological Processes, 2018, 32(18): 2915-2921.

[17] BAI X, SHAO M A, JIA X X, et al. Prediction of the van Genuchten model soil hydraulic parameters for the 5-m soil profile in China’s Loess Plateau[J]. Catena, 2022, 210: 105889.

[18] van GENUCHTEN M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal, 1980, 44: 892-898.

[19] 卢佳宇，王辉，欧阳赞. 低盐再生水灌溉对亚热带红壤水力特性及微观结构的影响[J]. 农业工程学报，2022，38(18)：103-112.

LU Jiayu, WANG Hui, OUYANG Zan. Effects of low-salinity reclaimed wastewater irrigation on the hydraulic properties and microstructure of subtropical red soil[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2022, 38(18): 103-112. (in Chinese with English abstract)

[20] 雷志栋，杨诗秀，谢森传. 土壤水动力学[M]. 北京：清华大学出版社，1988.

[21] ZHAO C L, SHAO M A, JIA X X, et al. Using pedotransfer functions to estimate soil hydraulic conductivity in the Loess Plateau of China[J]. Catena, 2016, 143: 1-6.

[22] WANG Y Q, SHAO M A, LIU Z P, et al. Prediction of bulk density of soils in the Loess Plateau Region of China[J]. Surveys in Geophysics, 2014, 35(2): 395-413.

[23] 冯正江，聂卫波，余淼，等. 多尺度土壤入渗特性的变异特征和传递函数构建[J]. 农业工程学报，2022，38(13)：64-75.

FENG Zhengjiang, NIE Weibo, YU Miao, et al. Multiple scale variability of soil infiltration characteristics and establishment of pedo-transfer function[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2022, 38(13): 64-75. (in Chinese with English abstract)

[24] 焦李成，杨淑媛，刘芳，等. 神经网络七十年：回顾与展望[J]. 计算机学报，2016，39(8)：1697-1716.

JIAO Licheng, YANG Shuyuan, LIU Fang, et al. Seventy years beyond neural networks: Retrospect and prospect[J]. Chinese Journal of Computers, 2016, 39(8): 1697-1716. (in Chinese with English abstract)

[25] 焦怀瑾，陈崇成，黄洪宇. 结合ICESat-2和GEDI的中国东南丘陵地区ASTERGDEM高程精度评价与修正[J]. 地球信息科学学报，2023，25(2)：409-420.

JIAO Huaijin, CHEN Chongcheng, HUANG Hongyu. Elevation accuracy evaluation and correction of ASTER GDEM in China southeast hilly region by combining ICESat-2 and GEDI data[J]. Journal of Geo-Information Science, 2023, 25(2): 409-420. (in Chinese with English abstract)

[26] 万华，高晓东，赵西宁，等. 黄土区苹果园土壤剖面水、汽通量模拟研究[J]. 土壤学报，2022，60(3)：1-14.

WANG Hua, GAO Xiaodong, ZHAO Xining, et al. Simulation of water and vapor fluxes in soil profile of apple orchard in Loess area[J]. Acta Pedologica Sinica, 2022, 60(3): 1-14. (in Chinese with English abstract)

[27] SU X L, MA L Y, WEI J M, et al. Structure and thermal stability of organo-vermiculite[J]. Applied Clay Science, 2016(132/133): 261-266.

[28] 郑旭，张宗俭，段韫丹，等. 湿润剂对基质水分吸持和白菜穴盘苗生长的影响[J]. 农业工程学报，2023，39(1)：188-194.

ZHENG Xu, ZHANG Zongjian, DUAN Yundan, et al. Effects of wetting agent application on substrate water absorption and Chinese cabbage plug seedlings[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2023, 39(1): 188-194. (in Chinese with English abstract)

[29] XING X G, KANG D G, MA X Y. Differences in loam water retention and shrinkage behavior: Effects of various types and concentrations of salt ions[J]. Soil & Tillage Research, 2017, 167: 61-72.

[30] 董义阳，赵成义，于志同，等. 古尔班通古特沙漠南缘丘间地土壤水分特征曲线及模拟[J]. 水土保持学报，2017，31(1): 166-171.

DONG Yiyang, ZHAO Chengyi, YU Zhitong, et al. Characteristic curves and models analysis of soil water in interdune at the southern edge of Gurbantunggut Desert[J]. Journal of Soil and Water Conservation, 2017, 31(1): 166-171. (in Chinese with English abstract)

[31] SCHAAP M G, van GENUCHTEN M T. A modified Mualem-van Genuchten formulation for improved description of the hydraulic conductivity near saturation[J]. Vadose Zone Journal, 2006, 5(1): 27-34.

[32] CORNELIS W M, RONSYN J, van MEIRVENNE M, et al. Evaluation of pedotransfer functions for predicting the soil moisture retention curve[J]. Soil Science Society of America Journal, 2001, 65: 638-648.

[33] AGYARE W A, PARK S J, VLEK P L G. Artificial neural network estimation of saturated hydraulic conductivity[J]. Vadose Zone Journal, 2007, 6: 423-431.

[34] PASCHALIS A, BONETTI S, GUO Y R, et al. On the uncertainty induced by pedotransfer functions in terrestrial biosphere modeling[J]. Water Resources Research, 2022, 58(9): e2021WR031871.

[35] 姚立忠，李太福，易军，等. 神经网络模型的透明化及输入变量约简[J]. 计算机科学，2012，39(9)：247-251，278.

YAO Lizhong, LI Taifu, YI Jun, et al. Visualize black-box of NN model and its application in dimensionality reduction[J]. Chinese Journal of Computers, 2012, 39(9): 247-251, 278. (in Chinese with English abstract)

Comparative analysis and prediction of the potting media water retention curve with different proportional compositions

ZHU Zhaocen1,2, SHAO Ming′an1,2,3, ZHAO Chunlei1,3※, JIA Xiaoxu1,3, WANG Jiao1,3

(1.,,100101,; 2.,,712100,; 3.,,100190,)

The water stress threshold is one of the most important indexes to evaluate the response of crops to water stress. Water control in the pot culture is also a commonly-used way to simulate drought stress conditions. The absorption of soil water by crops is mainly decided by the soil water potential. And the relationship between soil water content and water potential varies with matric medias. However, the water stress threshold of a crop is usually given in the form of mass water content. However, there is some inconsistency in the matric media under previous pot experiments. This study aims to rapidly obtain the water retention curves of base materials in the pot experiments, in order to predict the potting soil water retention curves. The peat soil, vermiculite, and perlite were taken as matric materials in the pot experiments. The water retention curves of various media were measured, including three kinds of matric materials and eight different proportional compositions. The van Genuchten model was used to fit these water retention curves. After that, the pedotransfer functions (PTFs) of water retention curves were established using multiple regression and artificial neural network. The normalized root mean square error (NRMSE), determination coefficient (2), and mean error (MR) were selected as the accuracy indicators of the model. Furthermore, the model stability was verified through 30 cycles to finally determine the optimal modeling and the predicted water retention curve. The results showed that an ideal fitting effect of the van Genuchten model was achieved in the water retention curves of (2>0.99). There were some significant differences in the water retention curves of the three potting medias. Peat soil presented more invalid pores than vermiculite and perlite, resulting in a large water content in the high-water suction section (water suction>100 kPa). The high capillary pore content of vermiculite led to a high-water content in the middle and high-water suction sections (water suction 33-800 kPa). Pearlite shared the higher permeability and low water holding capacity. Water was rapidly released with the increase of water suction. The prediction accuracies of the artificial neural network model for the peat soil water retention curves and vermiculite media materials were better than the multiple regression model. However, the opposite trend was observed for the peat soil and perlite media materials. Two different prediction models had different errors for the water retention curve parameters in the different media materials combinations. The multiple regression models often underestimated the prediction of saturated water content. As such, the multiple regression models underestimated the water content of media materials, compared with artificial neural networks under different water suction. The artificial neural network with PTFs reached a higher accuracy than the multiple regression with PTFs. The accuracy of multiple regression with PTFs had smaller variation and higher stability (smallerNRMSE, larger2, and mean error closer to 0), compared with the artificial neural network. Meanwhile, there was a large variance and distribution range ofNRMSE,2, andMRof PTFs developed by artificial neural networks, compared with the multiple regression. Therefore, better stability was achieved in the PTFs developed by multiple regression. In terms of accuracy and stability, multiple regression can be selected as the best to develop the water retention curve PTFs in various plot experiment medias. The finding can provide a strong reference for the rapid acquisition of water retention curves using the comparison between the pot water control experiments.

models; media materials; water stress; potting experiment; water retention curve; pedotransfer functions

2023-01-09

2023-02-28

中国科学院A类战略性先导科技专项资助（XDA28130100）；国家自然科学基金项目（41907009）；黄土高原土壤侵蚀与旱地农业国家重点实验室开放基金项目（A314021402–2014）

朱钊岑，博士生，研究方向为土壤物理和水文生态。Email：zhuzhaocen@nwafu.edu.cn

赵春雷，博士，副研究员，硕士生导师，研究方向为土壤物理和农业生态。Email：zhaocl@igsnrr.ac.cn

10.11975/j.issn.1002-6819.202301037

S152; S220.4

A

1002-6819(2023)-08-0197-08

朱钊岑，邵明安，赵春雷，等. 不同盆栽基质水分特征曲线的对比分析与模拟[J]. 农业工程学报，2023，39(8)：197-204. doi：10.11975/j.issn.1002-6819.202301037 http://www.tcsae.org

ZHU Zhaocen, SHAO Ming′an, ZHAO Chunlei, et al. Comparative analysis and prediction of the potting media water retention curve with different proportional compositions[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2023, 39(8): 197-204. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.202301037 http://www.tcsae.org