介电环境屏蔽效应对二维InX (X=Se,Te)激子结合能调控机制的理论研究*

段秀铭 易志军

(中国矿业大学材料与物理学院,徐州 221116)

采用基于格林函数的GW 方法计算发现: 孤立二维单层硒化铟(InSe)和碲化铟(InTe)具有吸收可见光的理想带隙,高的电子迁移率以及适合光解水的电子能带结构,电子自旋轨道耦合(SOC)效应使单层InTe从间接带隙半导体转变为直接带隙半导体.在准粒子能级计算的基础之上,通过求解Bethe-Salpeter 方程 (BSE)发现,孤立单层InSe 和InTe 的激子结合能远大于常温下激子的自发解离能.另一方面,实际应用的二维半导体为了维持其力学稳定性,大都需要依附在衬底上,另外,不同实验室样品自身原子层厚度也各异,这些因素必然改变二维半导体的介电环境.进一步的计算发现,二维InSe 和InTe 的激子结合能随自身原子层厚度以及衬底厚度的变大而减小,这说明可以通过调控二维半导体自身原子层以及衬底厚度的方式实现对激子结合能的精确调控,本文结果能够为将来精确调控二维InSe 和InTe 的激子结合能大小提供重要的理论依据.

1 引言

近年来,一种III-VI 族层状InSe 半导体因具有高的电子迁移率,良好的欧姆接触,以及良好的光学响应等独特的性能受到了研究者广泛的兴趣[1-6].然而,体结构InSe 的带隙只有1.25 eV[7,8],只能吸收近红外区间的光,这将限制其在太阳能领域的应用.在体结构的基础之上,也有报道通过机械剥离的方法[9]或者物理气相沉积法[10]成功制备出了只有原子层厚度的单层和数层二维结构InSe.与体结构InSe 相比,单层或者数层二维InSe 不仅具有高的电子迁移率[11],而且还有适合吸收可见光的理想带隙[1,2,12].除此之外,InTe 应用于中温区热电材料的研究也见报道[13].吸收可见光的理想带隙加上高的电子迁移率这些独特的性能,使得二维InSe 有潜力应用于未来太阳能领域.InTe 具有和InSe 类似的层状结构,依然具有高的载流子迁移率,并且体结构为直接带隙,大小为1.16 eV[14],略小于体结构InSe 的带隙.二维单层InTe 同样具有吸收可见光的电子能带结构以及高的载流子迁移率[15],因此也有应用于太阳能领域的潜力.

按照传统的基于能带理论的光催化机制,半导体除了具有吸收可见光的带隙以及高的载流子迁移率,如果还有合适的价带顶和导带底能级位置,即半导体的价带顶能级低于水的氧化电位,导带能级高于氢的还原电位,半导体还能用于光解水催化制氢.目前并没有实验报道孤立单层InSe 和InTe的导带顶和价带底的能级位置.虽然基于杂化泛函的HSE 方法也可以用于半导体电子能带结构的计算,但有文献报道,杂化泛函并不能正确描述低维结构材料体系的电子能带结构[16],就二维结构半导体而言,基于杂化泛函得到的带隙和精度更高的基于格林函数的GW 方法或者实验得到的带隙之间通常存在较大的差值,比如,采用HSE 计算得到的单层g-C3N4的带隙为2.9 eV,远小于基于格林函数的GW 方法得到的大约4.0 eV 的带隙[17,18],基于此原因,本文采用基于格林函数的GW 方法去系统性地计算InSe 和InTe 的价带顶和导带底能级位置.

另一方面,半导体应用于太阳能领域,除了需要高的载流子迁移率以及合适的电子能带结构外,也需要有大量自由的光生电子和空穴.如果半导体激子效应明显,在光照作用下,光生电子和空穴将很大程度上以激子的形式存在,如果激子结合能过大,必然抑制自由光生电子和空穴的产生,进而影响到太阳能光电性能.有研究报道原子层厚度的二维二硫化钼中激子的解离需要很大的外加电压[19].与传统的体结构材料不同,当层状半导体的厚度减小到单层或者数层原子层厚度后,由于几何约束以及电子之间的库仑屏蔽效应减弱,其激子结合能一般远远大于对应的体结构时的激子结合能,最大能够达到带隙的30%左右[20],大量研究报道,单层过渡金属硫化物(TMD)中的激子结合能为0.5—1.0 eV[21-24].然而常温下 (300 K) 激子的自发解离能 (exp(—kT)) 大约为69 meV.基于上述原因,孤立单层二维半导体材料的激子在常温下很难自发解离.另一方面,实验中制备的二维半导体材料不可能是孤立的,比如,为了维持二维半导体力学的稳定性,通常需要衬底材料去支撑二维半导体材料,或者为了避免直接和空气接触,将其封装起来[25].即便是二维半导体本身,实验使用样品的原子层厚度也各异.已有文献报道,衬底因素及其二维半导体自身原子层厚度的改变能导致二维半导体介电环境的改变[25-27],从而可以通过改变二维半导体介电环境实现对其激子结合能的调控[20],进而促进二维半导体中激发子的解离.目前,并不清楚二维InSe 和InTe 原子层自身厚度变化,以及衬底对其激子结合能的调控机制,因此有必要系统地研究环境的介电屏蔽效应对其激子结合能的影响,从而系统掌握介电屏蔽效应对其激子结合能的调控机制.

本文首先采用基于密度泛函理论的PBE 方法计算了InSe 和InTe 的电子能带结构以及电子和空穴的有效质量,在PBE 计算的基础之上,采用基于格林函数的GW 计算方法得到了孤立单层InSe和InTe 的准粒子带隙以及用于求解Bethe-Salpeter方程的屏蔽函数项,在此基础之上通过求解Bethe-Salpeter 方程计算了它们的光学吸收谱.在孤立单层InSe 和InTe 计算基础之上,系统研究了单层InSe和InTe 的激子结合能随自身原子层厚度变化的关系,以及衬底对单层和不同层厚度InSe 和InTe 的激子结合能的影响.

2 理论方法及其计算参数

对于几何结构优化以及基态性能的理论计算,本文采用基于密度泛函理论(DFT) 计算程序ASEGPAW[28].价电子和芯电子之间的相互作用采用的是投影缀加平面波(PAW)方法[29],交换关联项的描述采用广义梯度近似 (GGA) 下Perde-Burke-Ernzerhofe (PBE) 方法[30].本文使用平面波基组来展开波函数,相应的截断能为500 eV.为了构建二维InSe 和InTe 结构,真空层的厚度设置为15 Å来避免相邻两个超胞之间的相互作用.布里渊区的K点取样大小为12×12×1.为了保障计算精度,能量收敛标准为10—8eV.几何结构优化采用Broyden-Fletcher-Goldfarb-Shanno (BFGS)方法[31],力的收敛标准为每个原子的力小于10—4eV/Å.

基于基态的PBE 方法不能正确描述材料的电子结构,我们也采用了基于多体微扰理论的GW方法[32,33]来进行电子结构计算.在GW 计算部分,自能项 (self-energy) 的计算在实空间采用全频率积分方法.对于二维结构材料的计算,相比于DFT计算,GW 计算需要更大的真空层厚度来避免晶胞和相邻镜像晶胞之间的长程库仑相互作用[25,34],本文使用二维截断库仑势 (2D truncation) 方法[35,36]来减小GW 计算所用的真空层厚度,用到的真空层厚度为15 Å.二维介电函数在q趋近于0 时,很难收敛,布里渊区需要高密度的K点取样,当q趋近于0 时,我们采用文献[37]中所介绍的解析表达式来减小GW 计算所用的K点数量,在实际的GW计算部分,布里渊区K点取样和基态性能计算部分保持一致,依然为12×12×1.除此之外,包括GW计算在内的电子能带结构计算,都考虑了自旋轨道耦合效应 (SOC)[38].与DFT 计算不一样,GW 计算完全收敛需要很大的平面波截断能量,我们采取文献[39-41]所用的方法,取三个截断能86,92和100 eV,然后采用线性拟合方法将其截断能外推到无穷大,从而获得收敛的GW 计算结果.GW计算部分,需要一定数量的导带才能获得收敛的结果,我们将导带数量设置成和平面波基组的数量一致[41].

考虑到二维材料中的激子效应明显,采用GWBSE 方法[42]来完成单层InSe 和InTe 吸收光谱的计算,作为比较,我们也采用了文献[41]所介绍的无规相近似 (RPA) 方法完成了吸收光谱的计算(RPA 方法不包含激子效应),吸收光谱计算具体方法如附录A 所示.在吸收光谱计算过程中,响应函数平面波截断能取50 eV,导带数量设置成价带数量的5 倍,采用的展宽因子为0.05 eV.吸收光谱计算需要大量的K点才能获得收敛的结果,针对InSe 和InTe,布里渊区K点取样为36×36×1.

虽然GW-BSE 方法能够精确描述激子效应,但由于计算量的巨大,目前仅仅只能够针对小体系求解,对于多层结构激子结合能的计算,避免使用经验的Wannier 激子模型[43],采用了高精度的量子静电异质结 (QEH)[44]方法来进行激子结合能计算,其中用到的单层InSe 和InTe 以及单层h-BN的介电响应函数计算用到的参数和光谱计算参数一致.

3 结果和讨论

几何结构优化后的InSe 和InTe 空间群为P6m2 (No.187),原胞中具有4 个原子.二维晶体呈现蜂巢结构,如图1(a)所示,两个互相成键的In 原子位于两个Se/Te 原子层之间,对于单层InSe,优化后的晶格参数分别为a=b=4.07 Å;对于单层InTe,优化后的晶格参数为a=b=4.36 Å.沿c方向,对于单层InSe,两个相邻Se 原子的距离为dSe-Se=5.37 Å,两个相邻In 原子的距离dIn-In=2.81 Å,和文献结果一致[45];对于单层InTe,两个相邻Te 原子的距离dTe-Te=5.57 Å,大于InSe 中对应两个相邻Se 原子间距大约为0.2 Å,这是由于Te 相对于Se 元素具有更大的原子序数,从而导致Se-In 之间相对于Te-In 之间具有更强的库仑吸引力,使得dTe-Te大于dSe-Se,两个相邻In 原子的距离为2.81 Å,基本和InSe 两个相邻In 原子间距相等.

为了理解单层InSe 和InTe 的电子结构,使用了基于广义梯度近似的PBE 方法,分别计算了它们的电子能带结构,如图2(a)和图2(c)所示.计算电子能带结构所选取的倒格矢以及高对称K点分布如图1(b)所示.作为比较,也给出了不包含SOC效应的能带结构,如图2(a)和图2(c)所示(蓝色虚线).对于InSe 而言,SOC 效应导致了K点附近(Γ点到M点之间)导带边能级的分裂,位于K点附近价带边也存在能级分裂.同样,SOC 效应也导致了InTe 从Γ点到M点之间导带边能级的分裂,位于K点附近的价带边也出现了能级分裂.InTe的能级分裂相对InSe 更明显,其原因在于Te 的原子序数要大于Se,相对论效应更明显,所以能级分裂相较于InSe 更明显.如果不考虑SOC 效应,InSe和InTe 都是间隙半导体,导带底位置在Γ点,而价带顶都不在Γ点,如能带结构图中方框内所示.一旦考虑到SOC 效应,InTe 的价带顶和导带顶都位于Γ点,变成了直隙半导体,这可能是由于InTe在Γ点处存在Rashba 自旋分裂,导致Γ点能级发生改变,从而使价带顶位置从Γ点附近移动到了Γ点位置.从太阳能领域应用的角度去考虑,InTe 的电子结构要优于InSe.为了进一步理解InSe 和InTe 的电子结构,其相应的原子投影能态密度如图2(b)和图2(d) 所示.InSe 和InTe 的导带底主要由In 的s 轨道以及Se/Te 的p 轨道构成,而价带顶主要由In 的p 轨道以及Se/Te 的p 轨道构成.应用于太阳能领域的半导体,除了应该具有合适的电子能带结构外,也要求具有高的载流子迁移率,而载流子的迁移率和有效质量有关,载流子有效质量越小,其迁移率将越高.为了计算孤立单层InSe 和InTe 的载流子有效质量大小,针对InSe和InTe 能带结构图中Γ点,能量区间100 meV 以内的导带边和价带边采用抛物线拟合方法,计算了孤立单层InSe 和InTe 的电子和空穴有效质量,具体抛物线拟合后的详细过程如附录B 所示,具体结果记录在表1 中.如表1 所列,InSe 和InTe 都具有很小的有效电子质量(分别为0.17m0和0.13m0),这说明它们的电子迁移率会很高,早先的文献也证实了InSe 和InTe 具有很高的电子迁移率[3,15],相对于InSe 载流子的有效质量而言,InTe 的电子和空穴的有效质量更小,说明InTe 载流子迁移率会更高一些.

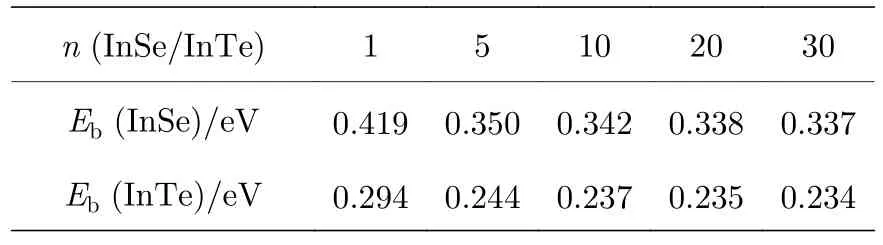
表1 InSe 和InTe 导带和价带带边电子和空穴的有效质量Table 1. The effective masses of electrons and holes of conduction and valence band edges for InSe and InTe.

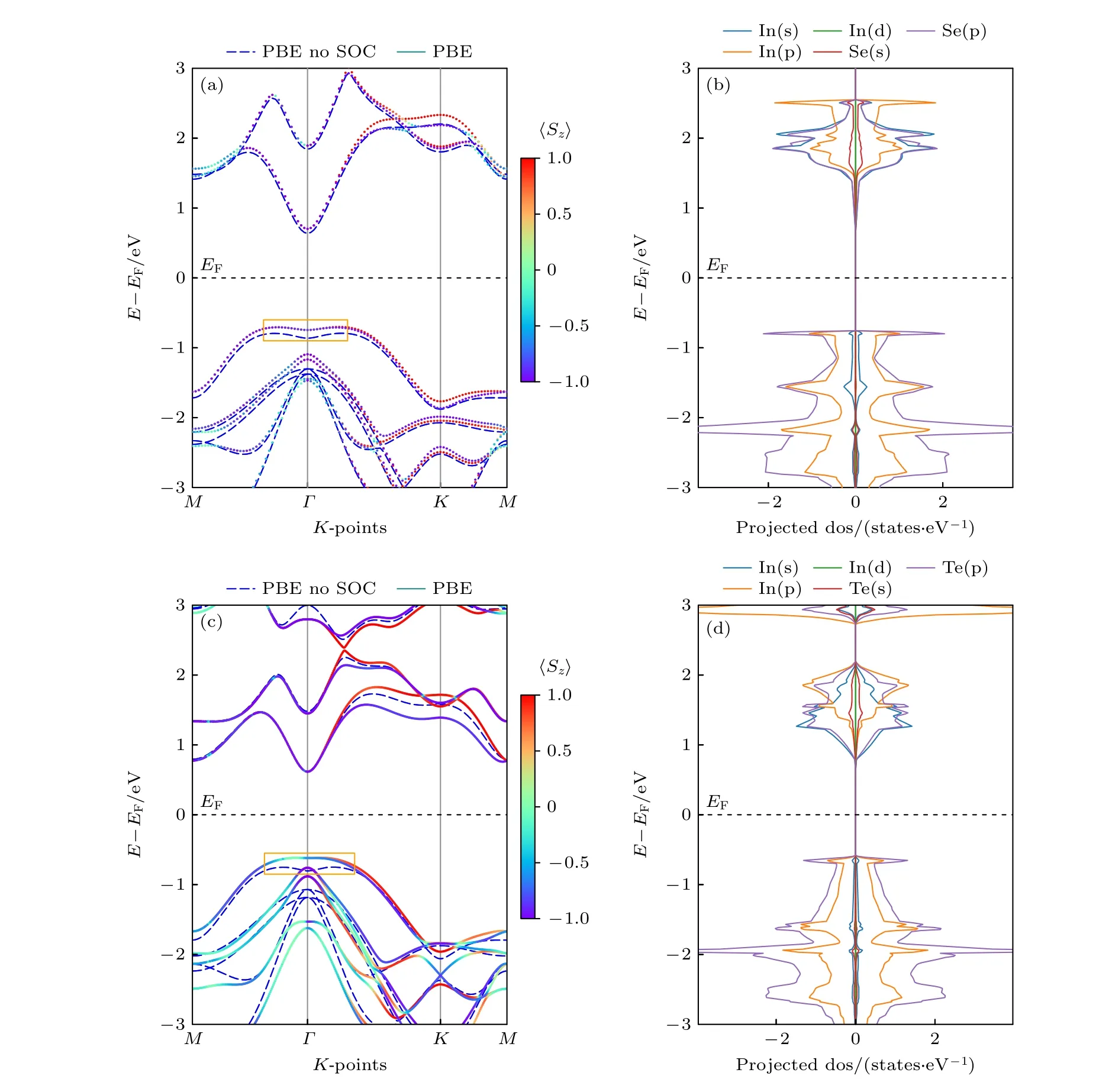
图2 孤立单层InSe (a),(b) 和InTe (c),(d) 的能带结构(左)和原子投影分态密度(右)Fig.2.The band structures (left) and atom projected density of states (right) of isolated monolayer InSe (a),(b) and InTe (c),(d).

半导体在现代光电子器件中的应用,除了要求具有高的载流子迁移率外,另一个重要因素就是要具有吸收可见光的理想带隙.基于基态的PBE 方法被公认会低估半导体的能隙大小,因此,目前广泛采用基于杂化泛函的HSE 方法计算半导体的能隙大小,但有文献表明,HSE 方法并不能很好描述低维材料的电子结构[16,34,46],因此针对二维体系,本文采用精度更高的基于格林函数的GW 方法来计算它们的电子结构.作为比较,分别采用PBE和GW 方法得到孤立单层InSe 和InTe 材料的准粒子带隙如图3(a)所示.单层InSe 和InTe 的PBE带隙分别为1.40 eV和1.19 eV,其值都小于对应的利用GW 方法得到的带隙.针对单层InSe 而言,对应的准粒子带隙大小为2.78 eV,对应的波长为445 nm,为可见光紫光区域.针对单层InTe 而言,其准粒子带隙大小为2.39 eV,对应的波长为519 nm,为可见光绿光波段.从上述结果来看,不管是孤立单层InSe 还是InTe 都能够吸收可见光.

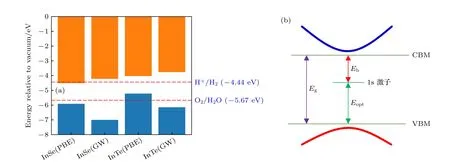
图3 (a) 基于PBE 和GW 方法得到的孤立单层InSe 和InTe 带边能级排列示意图;(b) 准粒子能级,光学带隙以及激子结合能示意图Fig.3.(a) The band edge alignments of isolated monolayer InSe and InTe based on PBE and GW method;(b) quasi-particle energy level,optical band gap and schematic diagram of exciton binding energy.

从作为太阳能光解水这方面的应用角度来看,通过和水的氧化电位和氢的还原电位相比较,InSe和InTe 都满足光解水催化制氢的能级匹配基本要求,尤其是孤立单层InTe,其价带顶和导带底更靠近水的氧化电位和氢的还原电位,比InSe 具有更理想的能级排列.另外,如前文所述,InSe 和InTe都具有较小的电子有效质量,以及具备吸收可见光的能隙大小,尤其是InTe,其电子能带结构显示为直隙半导体,相对于InSe 而言,具有更理想的电子能带结构用于光解水催化制氢.事实上,除了最基本的能级匹配,带隙大小以及载流子的迁移率外,影响光解水催化制氢的因素还有很多,在众多因素中,激子能否容易解离对其是否具备光解水催化制氢能力以及催化制氢效率也起到至关重要的作用.如果半导体应用于太阳能光伏领域,激子能否容易解离也同样起到关键性的作用.

影响激子解离的一个重要因素为激子结合能的大小.激子结合能为准粒子带隙和光学带隙之差,如图3(b)所示.准粒子带隙为GW 方法得到的准粒子能级价带顶到导带底的能极差,如图3(a)所示,对应实验中的光电子带隙.而光学带隙为价带顶到最低激子能级之差,如图3(b)所示,这个带隙大小可以直接从实验中的吸收光谱或者通过求解基于格林函数的Bethe-Salpeter 方程得出的光学吸收谱给出,如图4 所示.图4(a)和图4(b)分别对应的是单层InSe 沿平面和垂直于平面方向的光学吸收谱,图4(c)和图4(d)对应的分别是单层InTe 沿平面和垂直于平面方向的光学吸收谱.作为比较,图4 中也展示了采用基于单粒子近似的RPA 方法计算得到的光学吸收谱(蓝色实线),不同于RPA 方法得到的光学吸收谱,采用基于格林函数的BSE 方法得到的光学吸收谱,在准粒子带隙中存在明显的激子吸收峰,相应的激子结合能大小为光电子带隙和光学带隙之差,如图3(b)所示.单层InSe 和InTe 的激子结合能分别为0.66 eV和0.43 eV,根据图4 的光学吸收谱,单层InSe 和InTe 的光学带隙分别为2.15 eV 和1.96 eV.由于激子能级的存在,单层InSe 和InTe 的光学带隙明显小于其对应的准粒子带隙(光电子带隙).通常在激子结合能较小的一些体结构材料以及金属体系中,由于激子结合能通常不到0.1 eV,其光电子带隙和光学带隙之间的差别才可以忽略不计,但对于激子结合能较大的体系,比如二维半导体材料体系,其差值一般很大,因此必须考虑到光电子带隙和光学带隙之间的差别,孤立的单层二维半导体中较大的激子结合能也说明如果激子要解离成自由的电子和空穴,其难度也远大于相应的体结构材料.就孤立单层InSe 和InTe 而言,它们的激子结合能远大于常温下激子的解离能,尤其是孤立的InSe,激子结合能接近0.7 eV,这必然影响到自由光生电子和空穴的产生,从而限制它们在太阳能领域的应用.

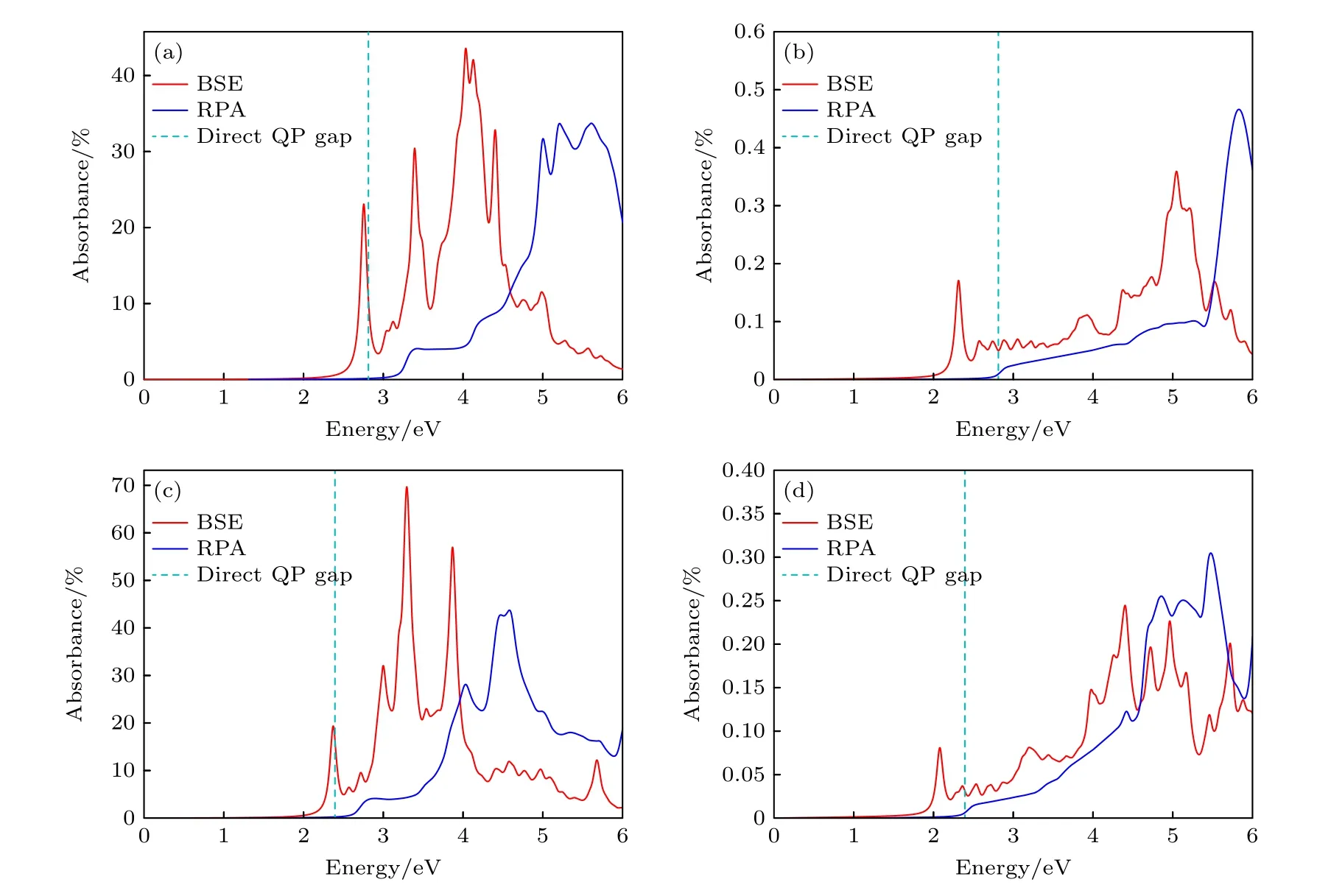
图4 单层InSe (a),(b)和单层InTe (c),(d)分别沿x 和z 方向的光学吸收谱Fig.4.The absorption spectrum of monolayer InSe (a),(b) and monolayer InTe (c),(d) along x and z polarization directions.

已经有研究报道,环境的介电屏蔽效应对二维黑磷以及过渡金属硫化物等二维结构材料的激子结合能有重要的影响[25-27],因此,可以通过调控二维半导体环境的介电屏蔽效应去调控相应的激子结合能大小,通常环境的介电屏蔽效应主要来源于二维半导体自身原子层的厚度以及所依附的衬底材料.就半导体自身原子层厚度而言,通常随原子层数的减小,由于库仑屏蔽效应的减弱,激子结合能逐渐增加,因此,孤立结构的单层二维半导体的激子结合能通常要大于其对应体结构时的激子结合能,过大的激子结合能必然影响到激子的解离.激子结合能的计算通常需要通过求解基于格林函数的Bethe-Salpeter 方程得到,然而求解Bethe-Salpeter 方程,由于计算量随原子数的增多成几何级数增加,目前仅仅只能针对小型体系求解,对于体系包含有数百个原子以上的大型系统,以目前的计算资源,很难通过求解Bethe-Salpeter 方程得到激子结合能.针对层状结构的二维材料而言,考虑到电子和空穴在垂直于半导体方向的有效质量很大,因此,只需要考虑电子和空穴在层内运动,相应地,三维的哈密顿量可以简化成二维问题[44],激子结合能可由下式给出:

通过上述方法,首先计算了孤立的二维InSe和InTe,在计算过程中用到的原子层厚度最大为30 层,相应的激子结合能随原子层厚度关系如图5所示,孤立单层InSe 和InTe 的激子结合能分别为0.67 eV 和0.47 eV,非常接近和通过直接求解Bethe-Salpeter 方程得到的孤立单层InSe 和InTe的激子结合能.因此,忽略电子和空穴沿垂直平面方向的运动,并不会在很大成程度上影响激子结合能的大小.在不到5 个原子层厚度的情况下,激子结合能变化量达到了约0.25 eV,随著原子层数厚度的增加,相应InSe 和InTe 的激子结合能逐渐减小,并且分别收敛到0.34 eV 和0.23 eV.

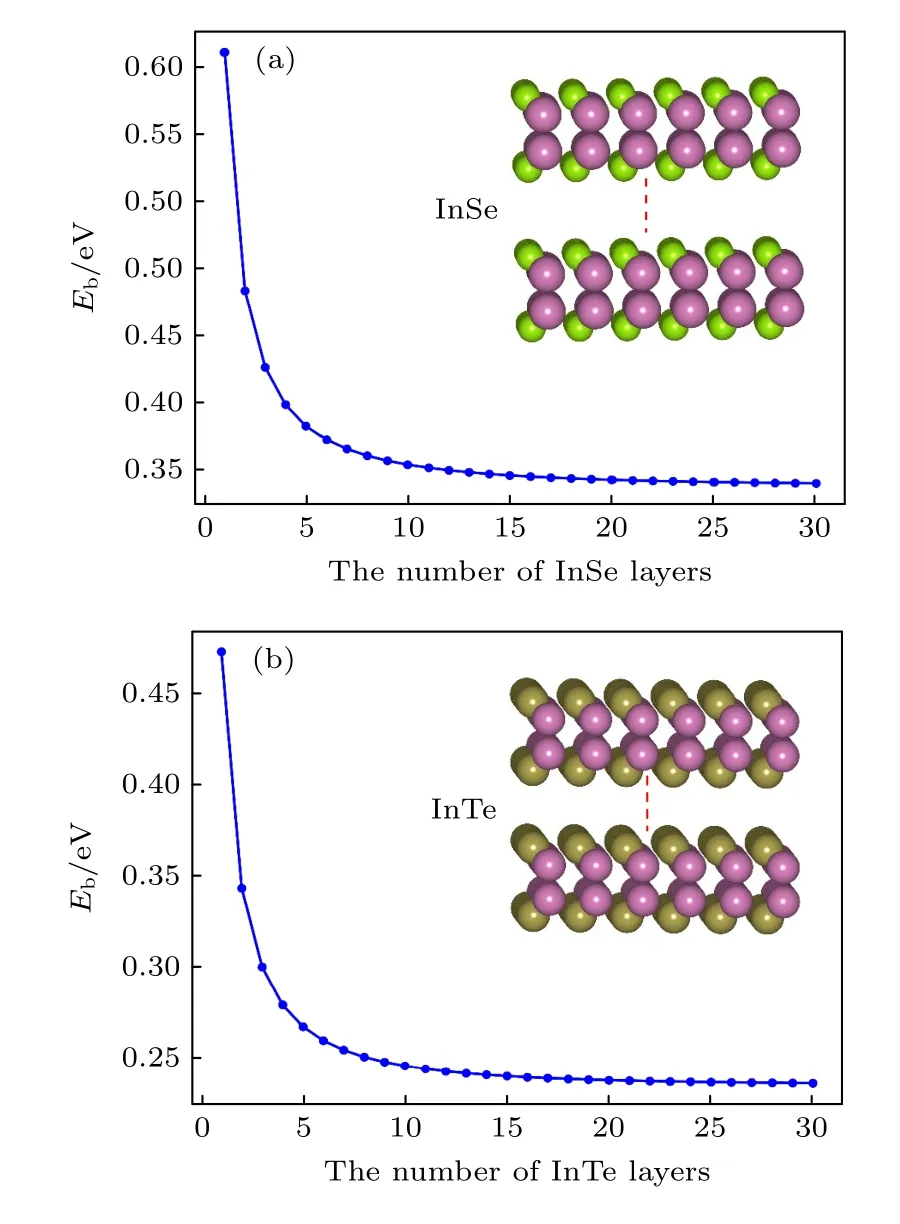
图5 InSe (a)和InTe (b)的激子结合能随自身原子层数量的变化关系Fig.5.The relationship diagrams of exciton binding energies of InSe and InTe with the variation of their self-atomic layer numbers.

激子结合能之所以随原子层厚度变化而改变,来源于二维半导体的介电函数随环境发生变化,如图6 所示为单层InSe/InTe 和环境之间的结构示意图,其中环境可以为真空层,也可以是其他的InSe/InTe 原子层或者其他衬底材料原子层.根据多体微扰理论可知,由于电子受周边其他电子的库仑屏蔽作用,电荷之间的库仑相互作用v应该由相互作用较弱的屏蔽函数W=ε-1v替换,屏蔽函数取决于介电函数ε.如图6 所示,孤立二维单层InSe/InTe 的介电函数为ε,其周边环境的介电函数为ε′,但环境为真空环境或者空气环境时,其介电函数对应的静态介电常数为1,此时孤立单层InSe/InTe 中电荷之间的相互作用不再受来自于邻近原子层的库仑屏蔽作用,电荷之间的库仑作用相对增强,当周边环境为不同厚度衬底或者InSe/InTe 原子层时,ε′也相应随衬底或者InSe/InTe原子层的增加而变大,因而使得InSe/InTe 层内的库仑相互作用随ε′的变大而减弱,又根据方程(1)可知,激子结合能的计算依赖于屏蔽函数W,当孤立二维半导体的环境因素发生改变时,其介电函数ε也相应发生改变,相应地屏蔽函数W也发生改变,必然导致其激子结合能发生改变.

图6 单层InSe/InTe 和环境之间的结构示意图Fig.6.The structural diagram between monolayer InSe/InTe and environment.

根据以上解释,当InSe/InTe 具有衬底材料时,衬底材料必然改变InSe/InTe 的激子结合能.为了理解衬底材料对二维InSe 以及InTe 的激子结合能的影响,以层状h-BN 材料作为它们的衬底材料来计算单层InSe 和InTe 的激子结合能随h-BN 原子层数的变化关系,如图7 所示.在计算过程中h-BN 的原子层最多达到50 层.如图7 所示,随着h-BN 衬底材料原子层数的增加,InSe 和InTe 的激子结合能随衬底原子层的厚度增加而减小,当衬底厚度为50 个原子层厚度时,InSe 的激子结合能减小到0.42 eV,而单层InTe 的激子结合能减小到0.29 eV.为了理解不同厚度的InSe和InTe 在一定厚度衬底上的激子结合能的变化关系,我们分别计算了1 层,5 层,10 层,20 层以及30 个原子层厚度的InSe 和InTe 在50 个原子层固定厚度的h-BN 衬底上时的激子结合能,如表2所列,当30 个原子层厚度的InSe 和InTe 在50 个原子层厚度的h-BN 衬底上时,其激子结合能分别为0.34 eV 和0.23 eV.

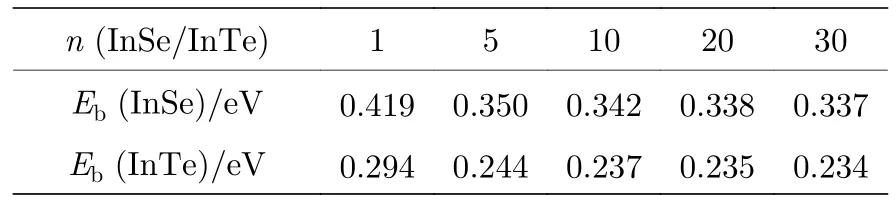
表2 不同原子层厚度InSe 以及InTe 放置在50 个原子层厚度h-BN 衬底上时的激子结合能Table 2. The exciton binding energies for different atomic thicknesses of InSe and InTe on h-BN substrate with 50 atomic layer thickness.

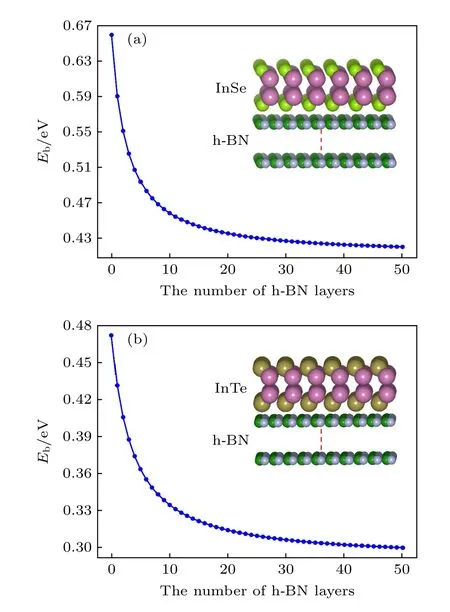
图7 单层InSe (a) 和InTe (b) 的激子结合能随h-BN 原子层数量的变化关系Fig.7.The relationship diagrams of exciton binding energies of monolayer InSe and InTe with the variation of number of h-BN atomic layers.

通过以上结果,可以得出,InSe 和InTe 的激子结合能可以通过改变自身原子层厚度以及衬底厚度取精确调控.未来设计用于太阳能领域的半导体材料,不仅需要考虑到基本的带隙,能带结构,更要考虑半导体自身原子层厚度以及衬底材料厚度等因素对其光催化性能的影响,尤其是在不到5 个原子层厚度的情况下,体系的激子效应十分明显.

4 结论

采用基于格林函数的GW 计算表明,孤立二维单层InSe 和InTe 具有吸收可见光的理想带隙,高的电子迁移率,以及适合光解水的电子能带结构.但通过求解Bethe-Salpeter 方程发现: 孤立单层InSe 和InTe 中激子结合能分别为0.66 eV 和0.43 eV,远大于常温下激子的自发解离能.进一步的计算发现,二维InSe 和InTe 中激子结合能随自身原子层厚度以及衬底厚度的变大而减小,这也说明可以通过调控二维半导体自身原子层以及衬底厚度的方式实现对激子结合能的精确调控,我们的结果能够为将来精确调控二维InSe 和InTe 中激子结合能大小提供重要的理论依据.

附录A 二维结构材料吸收光谱计算

无规相近似(R PA):

式中c为光速α2D,由下式给出:

式中L为垂直二维原胞晶面方向的长度,介电函数ε由下式给出:

式中v为库仑作用项目,并且有如下关系:

式中V为原胞体积,χ为响应函数,满足Dyson 方程:

式中χirr是不可约布里渊区间响应函数,在无规相近似(RPA)下,χirr由无相互作用的响应函数χ0代替.实际计算过程中χ0展开如下:

式中ψ和ε分别为PBE 计算得到的波函数和本征值,G为倒格矢,q为布里渊区间k点的值,η为正的无穷小量,f为费米占据数.

Bethe-Salpeter 方程(BSE):

式中Ec和Ev分别为导带准粒子能量和价带准粒子能量,可以通过GW 计算得到,v和W分别为库仑作用项和屏蔽函数,分别由如下两式展开:

宏观介电函数表达式如下:

式中的虚部对应的是光学吸收谱,其中ω为频率格点,和Eλ为激子本征波函数和本征值,通过求解方程(A7)得到.

附录B

针对InSe 和InTe 能带结构图中Γ点能量区间100 meV以内的导带边和价带边,采用抛物线拟合方法来分别计算电子和空穴的有效质量,计算有效质量时,布里渊区间K点取样密度远大于电子能带电子结构的计算,这里取45.0/Å—1,K点均匀分布在半径为0.015 Å—1圆区间,计算电子和空穴有效质量我们也考虑了SOC 效应.InSe 和InTe沿a(图中方向1)和b(图中方向2)两个方向导带边和价带边抛物线拟合如图B1 所示.

图B1 InSe 和InTe 沿a (图中方向1)和b (图中方向2)两个方向导带边和价带边抛物线拟合Fig.B1.Fitted results of conduction band edge and valence band edge of InSe and InTe along both a (direction 1 in the figure) and b (direction 2 in the figure).