典型路面激励下的蓄电池框架动态响应研究

张瑞峰，冯勇淇，范政武

（1.江铃重型汽车有限公司，山西 太原 030032；2.太原理工大学车辆工程系，山西 太原 030024）

1 引言

2 蓄电池框架固有振动特性分析

经验模态分解（Empirical Mode Desperation，EMD）[1]依据信号本身的时间变化进行信号分解，不需要假设任何初始基函数。EMD在信号去噪、机械故障诊断和图像处理等方面得到广泛应用[2-4]。文献[5]针对工程自卸车的作业工况的随机特性，应用EMD方法重构车架振动信号，分析车架的动态响应特性，能够很好的去噪并保留信号原始特征。

为研究重型商用车蓄电池框架的动态性能，在典型路面（搓板路面）激励下的整车路试中采集蓄电池框关键位置振动信号。针对振动信号的非线性和非平稳特性，应用经验模态分解（EMD）和固有模态分析的方法，重新构建蓄电池框振动信号，对某重型商用车蓄电池框架动态响应研究，改善该蓄电池框架性能和使用寿命。

2.1 结构固有振动特性分析原理

汽车行驶振动为随机振动，汽车零部件的可靠性和耐久性能主要受随机振动的影响，分析其结构的固有振动特性是提高零部件可靠性和耐久性的基础工作。部件结构、自身质量和刚度分布所决定了结构件的固有振动特性，模态分析则是研究结构件在动态载荷作用下的响应，是结构动力学研究的主要方法，它采用实验和理论相结合的方法，是解决工程问题中由于振动引起的可靠性和耐久性问题的重要手段[6]。

其结构振动的模态方程为：

式中：K—刚度矩阵；M—质量矩阵；φ—固有振型；ω—固有频率。

通过求解上述方程组可获得信号各阶固有频率ωi和固有振型φi（i=1，…，N）。

2.2 蓄电池框架模态分析

模态分析是研究结构动态特性的一种方法，可分为计算模态分析和实验模态分析[7]。

这里研究的对象是某重型商用车蓄电池框架，采用计算分析和实验相结合的模态分析方法，以此来准确获得蓄电池框架的模态参数。

由于蓄电池框架安装固定在车架总成右侧，受外部约束和载荷的影响，因此这里对蓄电池框架进行了约束状态下的模态实验。试验蓄电池框架，如图1所示。综合频响函数，如图2所示。

图1 约束模态实验蓄电池框架Fig.1 Constraint Modal Experiment Battery Frame

图2 综合频响函数Fig.2 Integrated Frequency Response Function

蓄电池框架计算分析模态频率与实验分析对比结果，如表1所示。由表1可见，一阶模态频率的误差为5.3%，二阶模态频率的误差为0.43%，其余阶数的误差介于两者之间，计算精度满足动态分析要求。

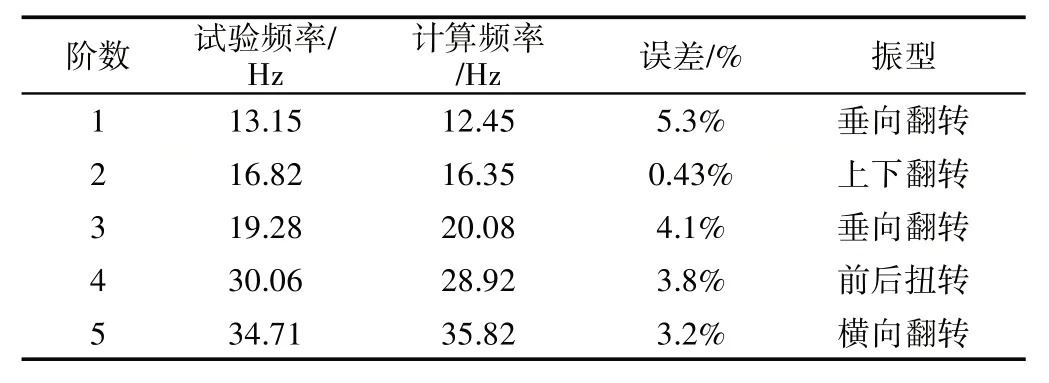
表1 模态分析频率Tab.1 Modal Analysis Frequency

3 典型路面下的振动试验

根据蓄电池框架的结构特点和模态振型，在车架连接部位和蓄电池框架上确定8个关键位置点，并布置安装了加速度传感器，采集各点三个方向加速度信号，具体安装位置，如图3所示。加速度传感器详细位置信息描述，如表2所示。

表2 加速度传感器安装位置Tab.2 Acceleration Sensor Mounting Position

图3 加速度传感器安装位置Fig.3 Acceleration Sensor Mounting Position

试验工况为满载40t，车速为60km/h，路况为搓板路面。采样时间为120s，重复采集数据3 次。针对采样数据分别进行处理，通过对处理后的结果进行分析。因路面的时变性，3次采集的数据虽有一定差异，但从总体趋势上对比基本保持一致，这里选择第3次数据为分析样本。搓板路路面下3、5、7处的垂直方向的时域响应，如图4所示。

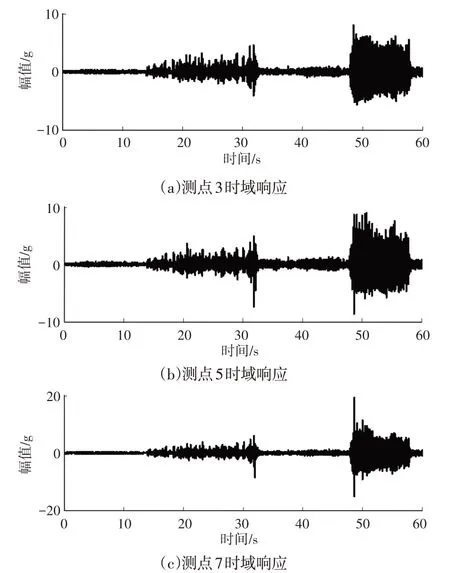
图4 搓板路测点3、5、7时域响应Fig.4 Points 3，5，7 Time Domain Response of Washboard Road

4 基于EMD典型路面动态响应分析

4.1 EMD算法信号去噪应用

重型商用车在搓板路面实验时，其振动响应具有非线性和非平稳的特性。

从图4的时域分析结果可以看出，由于受到路面和环境的影响，采集的蓄电池框架测点振动信号噪音大，成分复杂。

经验模态分解（Empirical Mode Desperation，EMD）[1]可以根据信号本身的时间变化来分解信号，省去了设定基函数，这是区别于典型的傅里叶和小波分解方法的最明显的特征。

该方法对处理非平稳及非线性振动信号具有非常明显的优势，且信噪比高[8]。

EMD算法假设对于任何信号都是由若干有限的IMF（本征模函数）组成，本征模态函数可以通过如下方法得到[1，9-11]：

采用三次样条曲线拟合方法拟合极值点包络线。则取：

式中：c1(t)—一阶IMF分量；(t)—经过k次分解后的新信号。过滤掉高频成分的信号为：

式中：r1(t)—过滤掉高频成分的信号。

重复上述过程，假定经过n次之后第n阶分量cn(t)或其残余量rn(t)不满足判断条件为止。

最后，x(t)经EMD分解后得到：

式中：ci(t)—第i阶IMF分量。

Flandrin等基于EMD分解的滤波特性提出一种构造滤波器组的新方法[12]。通过截取不同频率的IMF构造不同的滤波器。

（1）高通滤波器

过滤掉后部分低频IMF 分量，截取前部分高频IMF 分量来重新构建原始信号。

（2）低通滤波器

过滤掉前部分高频IMF 分量，截取后部分低频IMF 分量重新构建原始信号。

（3）带通滤波器

截取中间部分IMF分量重新构建原始信号。

（4）带阻滤波器

截取两端的IMF分量重新构建原始信号。

用EMD分解的IMF分量构建的滤波器组可以实现截取频率随输入信号的变化而变化，使其具有自适应的能力。把分解得到的残余量rn(t)作为第n个IMF分量，则带通滤波器可表达为：

式中：xbhk(t)—带通滤波信号；cj(t)—第j阶IMF分量。

4.2 基于EMD算法的蓄电池框动态响应分析

在试验场搓板路面进行动态实验采集的蓄电池框架振动信号包含动态响应信号，这里基于EMD分解算法，参考计算和试验模态分析结果，把约束模态频率作为EMD算法滤波的带通频率构建带通滤波器，对蓄电池框架振动信号进行分解重构，获取蓄电池框架的动态响应特性。

原始信号定义为测点2 的振动信号，其分析结果，如图5所示。

图5 x（t）的EMD分解IMF分量图Fig.5 x（t）EMD Decomposition IMF Component Graph

定义约束模态频率［5Hz，100Hz］范围作为EMD算法带通滤波的带通频率，对获得的本征模态函数IMF 分量进行频谱分析后，信号进行重构，其表达式如下：

测点3位置的原始振动信号时域图和EMD滤波重构后的振动信号时域响应图，如图6所示。

图6 测点3原始信号与重构信号对比Fig.6 Point 3Original Signal Compared with the Reconstructed Signal

从图6可以看出，振动信号的非线性和非平稳性得到保留，噪声和非关注频段信号则被滤除。

应用EMD方法，分别对优化前后采集到的数据进行频谱分析，重点对测点1，3，5，7，8所获得的响应信号进行处理，获得的各测点的频谱图，如图7～图11所示。

图7 测点1频谱图Fig.7 Point 1 Spectrum Graph

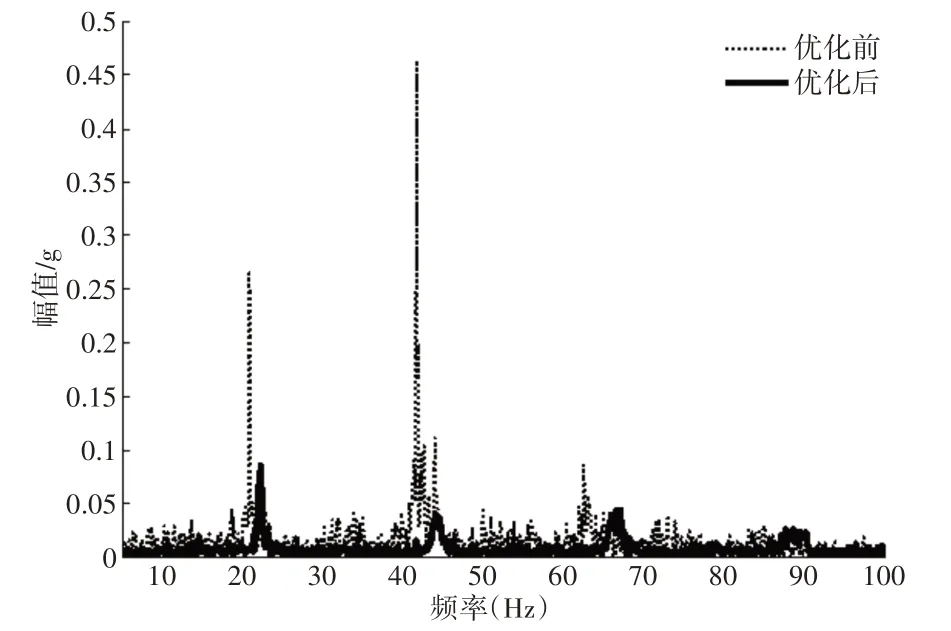
图8 测点3频谱图Fig.8 Point 3 Spectrum Graph

图9 测点5频谱图Fig.9 Point 5 Spectrum Graph

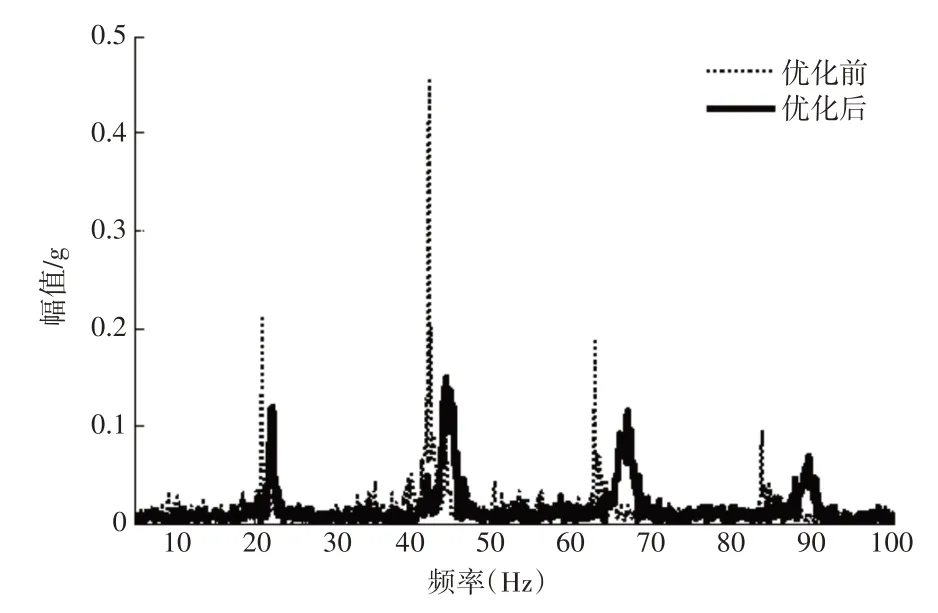
图10 测点7频谱图Fig.10 Point 7 Spectrum Graph

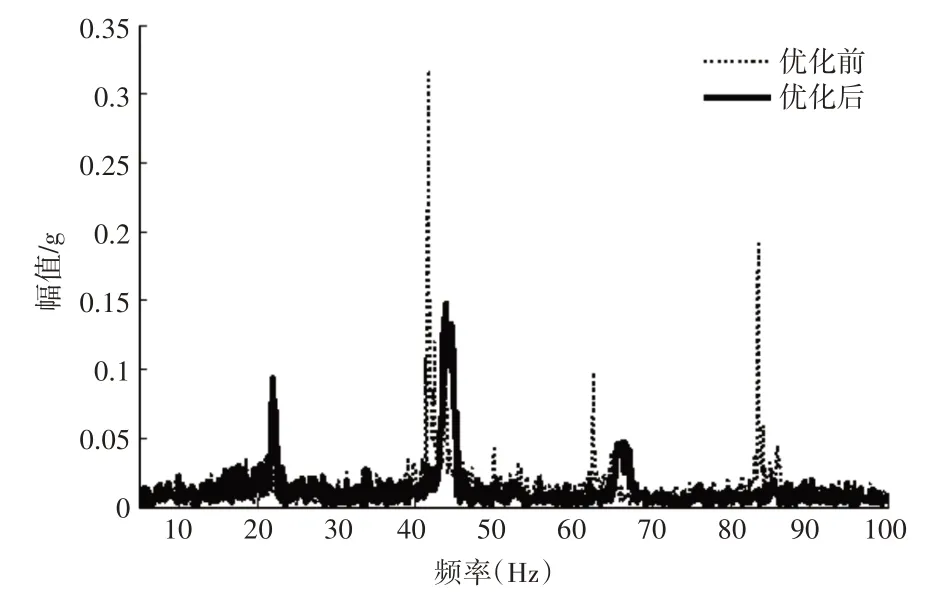
图11 测点8频谱图Fig.11 Point 8 Spectrum Graph

根据各个测点的频谱中的响应，结合约束模态分析结果，可以得出如下结论：

（1）当激励频率为21Hz，40Hz 时，各测点的振幅都较大，出现共振现象，这与模态试验测得（1～5）阶模态频率与振型基本吻合。

（2）当激励频率为65Hz，90Hz时，5，7，8测点的振幅也比较大，出现共振现象，而模态试验并未测得60Hz和90Hz的共振频率。分析认为主要是蓄电池的冲击造成的。

（3）优化前后对比，从图7～图11看出，各频率点的振幅都有了较大的改善。

各测点垂直振动加速度均方根值对比图，如图12所示。从该图可知，最小下降11.4%（测点7），最大下降58.7%（测点3）。振动状态有了明显的改善，提高了电瓶框架的寿命。

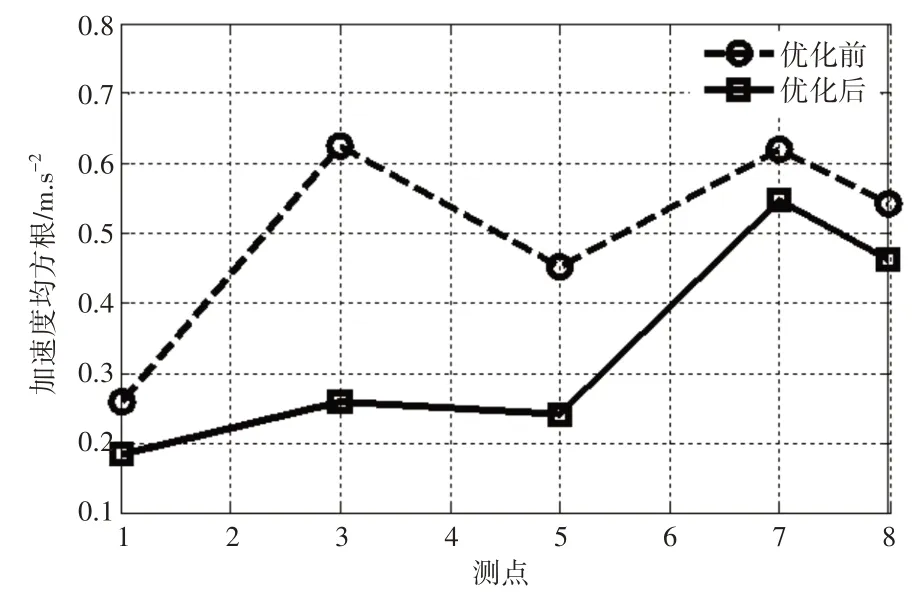
图12 优化前后加速度均方根对比图Fig.12 The Mean Square Comparison of Acceleration

5 结论

对如何解决典型工况下动态特征难以提取的难题，固有约束模态分析与EMD分解相结合是有一个效的解决方法。可有效的对采集到的振动信号进行分解和重构。分析结果表明，在搓板路面激励下，商用车蓄电池框在该典型路面运行时会出现共振现象，且由于其悬臂结构，在远离固定点的位置会出现振动放大现象，对蓄电池框造成疲劳破坏，对其结构优化，明显改善了其性能。基于EMD的典型路面下动态特性分析对商用车零部件结构优化具有一定的指导作用。