考虑真空加载过程的钉形搅拌复合地基固结解析解

袁晨露 杨涛

摘要：考虑真空负压力随时间变化，推导出真空预压下钉形水泥土搅拌桩复合地基的固结控制方 程和求解条件。将固结方程和求解条件进行函数变换，基于双层地基一维固结理论求解出桩间土 和复合地基加固区中的平均超静孔隙水压力， 然后获得了钉形搅拌桩复合地基的整体平均固结 度。通过与数值模拟结果的比较，验证了固结解析解的合理性。利用提出的固结解析解，分析了 桩置换率、扩大头尺寸、桩间土刚度及真空加载参数等因素对复合地基固结的影响。研究结果表明：真空下钉形搅拌桩复合地基的固结速率随桩置换率、扩大头高度和其下桩间土压缩模量的增 加而增大， 固结前期固结速率随扩大头半径的增加而增大， 固结后期则影响很小。真空加载过程 对复合地基的固结过程几乎没有影响。

关键词： 钉形搅拌桩 ；解析解 ；真空加载过程 ； 固结 ；复合地基

中图分类号：  TU 473             文献标志码：   A

Analytical solution for consolidation of composite ground with T-shaped deep cement mixing columns considering vacuum loading process

YUAN Chenlu， YANG Tao

（School of Environment and Architecture， University of Shanghai for Science and Technology， Shanghai 200093， China）

Abstract： Considering change in negative vacuum pressure with time， the governing equations and the corresponding solution conditions for consolidation of the composite ground with T-shaped deep cement mixing （TDM） columns under vacuum preloading were derived. Based on one dimensional consolidation theory of a double-layersoil ground， the average excess pore water pressures within the improved zones and the surrounding soil were obtained by the functional transformation of the consolidation equations and solution conditions. The overall average consolidation degree of the composite ground with TDM columns was presented. Then， the rationality of the proposed solutions was verified by comparison with the numerical simulation results. Finally， the influence of the replacement ratio of the column， the column cap size， the stiffness of the surrounding soil and the vacuum loading parameter on the consolidation rate of the composite ground was investigated using the proposed solution.The results indicate that the consolidation rate of the composite ground increases with increasing the replacement ratio of the column ， the height of its cap and the constrained modulus of the soil under the column cap. The consolidation is accelerated with increasing the radius of column cap in the early stage of consolidation， but it has insignificant influence in the later stage of consolidation process. The vacuum loading process has little effect on the consolidation of the composite ground.

Keywords：  TDM  column; analytical  solution; vacuum  loading process; consolidation; composite ground

真空預压作为重要的排水固结法，是在地表封闭模下的砂垫层中抽真空，真空度通过地表砂垫层和打入地基中的排水体传递给地基土从而加速其固结，地基土的固结是在负孔压下进行固结的。传统的堆载预压法和真空预压法联合使用，增大了预压荷载，提高了地基土的固结速率，复合地基的稳定性更高，在国内外得到了广泛应用[1-3]。

目前，真空和真空?堆载联合作用下砂井地基固结理论研究获得了较大进展。 Indraratna 等[4]考虑砂井中的真空度呈线性衰减，建立了真空下砂井地基径向固结解析解。韩文君等[5]对 Indraratna 等[4]的解析解作了改进，建立的解析解考虑了地基土非线性的影响。张玉国等[6]考虑涂抹区径向渗透系数变化，给出了真空预压下变径阻砂井地基的径向固结解析解。郭彪等[7]在变荷载和真空预压的共同作用下，建立了考虑真空度呈线性衰减、涂抹区径向渗透系数变化以及竖向附加应力非均匀分布条件下砂井地基的固结解析解。林伟岸等[8]考虑了荷载和真空度均随时间变化、真空度沿地基径向与竖向衰减、井阻和涂抹效应的真空?堆载下砂井地基固结的普遍解析解。田乙等[9] 假设真空和荷载均瞬时施加，建立了真空?堆载联合作用条件下未打穿竖向砂井地基的固结解析解。

随着桩体加固技术在软土地基加固中的应用日益广泛，近年来真空和真空?堆载联合作用下复合地基固结理论研究开始受到学者们的关注。叶观宝等[10]给出了荷载和真空均为瞬时施加的混凝土芯砂石桩复合地基径向固结解析解。张丹贝等[11]将加固区的桩?土均质化，获得了真空下悬浮不排水桩复合地基固结简化解。张玉国等[12-13]建立了真空和堆载瞬时施加时散体材料桩复合地基径向固结解析解，考虑了地基中竖向附加应力和桩体中真空度的线性衰减。

综上可见，目前考虑真空作用的复合地基固结解析理论的研究成果不多。钉形搅拌桩是变截面水泥土搅拌桩，它是由上部大直径的扩大头和下部小直径的搅拌桩组成。相较于传统的等直径搅拌桩复合地基，钉形搅拌桩复合地基的承载力更高。现有的钉形搅拌桩复合地基固结理论[14-15]都是针对荷載作用提出的，并没有考虑真空作用。本文的目的是建立真空下钉形搅拌桩复合地基固结计算模型，分析真空作用下这种新型复合地基的固结特性，进一步完善变截面水泥土搅拌桩复合地基的设计理论。

1 轴对称固结模型和基本假设

1.1 轴对称固结模型

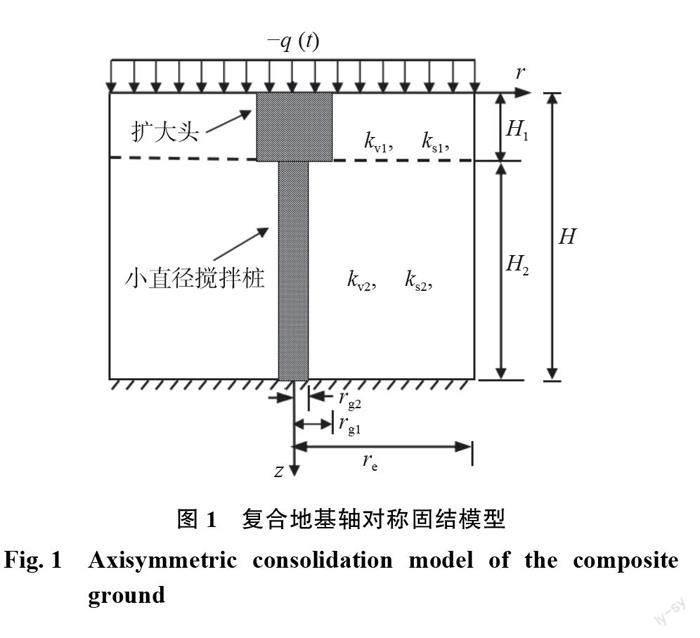
真空作用下端承钉形搅拌复合地基的轴对称固结模型如图1所示， r ，z 分别为系统的径向、竖向坐标。图中单桩影响区的半径为 re ，H 为钉形搅拌桩的总长度，也是复合地基的厚度。H1， H2分别为钉形搅拌桩上部扩大头的高度和下部小直径搅拌桩的长度， rg1，rg2分别为扩大头和下部小直径搅拌桩的半径。ρ=rg1/rg2，ρ为扩大头的扩径比， m=（rg2/re）2，m 为小直径桩的置换率，可推算出扩大头的置换率为 mρ2。根据扩大头的高度将整个复合地基加固区分成上、下两部分，同样将桩间土分成上、下两层。 kv1，Es1，kv2，Es2分别为上、下层桩间土的渗透系数和压缩模量， Ep1， Ep2分别为扩大头和其下部小直径搅拌桩的压缩模量。?q（t）为复合地基表面施加的真空负压力，?q（t）=?q0[1?exp（?αt）]， t 为时间， q0为设计的膜下真空度，α为反映真空加载过程的参数，在实际工程中，α值可由实测真空加载线按指数曲线拟合方法得到。

1.2 基本假设

本文公式推导中采用了如下基本假设：

a.桩与桩间土仅竖向变形，任意深度处两者竖向应变相等。

b.桩为不透水桩。桩间土完全饱和，水的渗流服从达西渗透定律。

c.处于扩大头正下方的环状土体仅发生径向渗流。

d.地表真空度沿地基深度不衰减。

e.固结过程中桩间土的渗透系数和压缩模量不发生变化。

2 固结控制方程及其解答

2.1 固结方程与定解条件

2.1.1上、下层桩间土的固结方程

参照杨涛等[14-15]的研究，可写出上、下层桩间土的固结方程为

式中：?（u）s1，?（u）s2分别为上、下层桩间土在任意深度z 处的平均超静孔隙水压力； cv1c ，cv2c 分别为考虑扩大头和小直径桩影响后上、下层桩间土的等效固结系数；γw 为水的重度； Ecs1，Ecs2分别为上、下加固区的复合压缩模量； cv1， cv2分别为上、下层桩间土的竖向固结系数， cv1=kv1Es1/γw ， cv2= kv2Es2/γw。

2.1.2 固结方程（1）的定解条件

竖向边界条件：

上、下加固区交界面上连续性条件：

初始条件：

2.2 固结方程与定解条件的变换

为了方便在定解条件式（6）～（10）下更直接地求解固结方程（1），先作如下的函数变换：

式中，?（u）1，?（u）2分别为复合地基中的上、下加固区任意深度的平均孔压。

将函数变换式（11）代入固结方程（1）和定解条件式（6）～（10），可得，

为使边界条件式（13）齐次化，再作如下函数变换：

式中， ws1，ws2为系数。

将式（18）和（19）代入式（12）～（17），可得，

3 固结解析解

3.1 超静孔压解答

方程式（20）及其定解条件式（21）～（25）与荷载为 q（t）下双层地基固结问题中的固结方程与定解条件在形式上是一致的，不同之处是上、下层土的平均超静孔压和固结系数分别用函数 wsi（z，t）和 cvic （i=1，2）来代替，故可利用谢康和[16]双层地基一维固结理论的方法直接求解。

为简化列式，定义 a ，b ，c 和μ这4个无量纲参数。

参照谢康和[16]的研究，可得，

λm 通过求解下面特征方程确定： pabtan （λm）tan （?cλm）=1（26）

将 q（t）= q0[1一exp （一αt）]代入式（27）～（28），可得，

将式（32）和（33）代入式（18）和（19），得到复合地基上、下加固区的平均超静孔隙水压力：

将式（34）和（35）代入式（11），得到上、下层桩间土中的平均超静孔隙水压力：

3.2 固结度解答

Chu 等[17]指出：相较于按沉降定义的固结度，真空荷载下采用按孔压定义的固结度更为合理。参照彭劼等[18]和张丹贝等[11]的研究，真空下钉形搅拌桩复合地基上、下加固区按孔压定义的固结度

式中，?（u）i为整个上、下加固区的平均超静孔压。

将式（34）和式（35）分别代入式（39）和式（40），再将式（39）和式（40）代入式（38），可得，

真空下钉形搅拌桩复合地基按孔压定义的整体平均固结度

将式（41）和式（42）代入式（43），可得，

4 算例验证

端承钉形水泥土搅拌桩复合地基厚度 H=16 m，扩大头高度和半径分别为 H1=4 m 和 rg1=0.5 m，下部小直径搅拌桩长度和半径分别为 H2=12 m 和 rg2=0.25 m ，单桩影响区半径 re=1.2 m ，扩大头的扩径比ρ=2。各材料参数：钉形搅拌桩压缩模量 Ep1=Ep2=Ep=120 MPa ，Ep 为桩的压缩模量，泊松比为0.25；上、下层桩间土的压缩模量 Es1=Es2=3 MPa，竖向渗透系数 kv1=kv2=10?7 cm/s；桩间土的泊松比为0.35。复合地基表面真空荷载为?q（t）=?80[1?exp（?t）]，即取 q0=80 kPa ，α=1.0 s?1。

分别采用本文建立的固结解析解和有限元法计算真空下钉形搅拌桩復合地基固结度并进行比较。有限元计算采用 ABAQUS 软件。取图1所示复合地基轴对称固结模型进行轴对称有限元固结计算，利用对称性可取其一半区域进行分析。数值计算时使模型左、右侧边界上不发生径向变形，即不产生径向位移，约束模型底部径、竖向变形，即不产生径、竖向的位移。模型的底部和左、右两侧面均不排水，复合地基表面自由且可以排水。在有限元固结计算中，各材料均为线弹性模型，其弹性模量 E 可由其压缩模量 E0和泊松比μ按式 E=（1+μ）（1?2μ）E0/（1?μ）近似计算。钉形搅拌桩用4结点CAX4单元离散，桩间土用应力?孔压耦合4结点CAX4P 单元离散，桩?土界面完全接触。在有限元固结计算中将桩间土表面作为已知孔压边界，其上用负孔压?q（t）模拟真空荷载。图2为模型的有限元网格示意图，单元总数1773个，结点总数1240个。

图3给出了由本文解析解和有限元法计算获得的钉形搅拌桩复合地基平均固结度和桩间土超静孔压随时间变化曲线的比较，横坐标为无量纲时间因数 Tv=cv1t/H2，孔压计算点位于有限元模型外侧边界上 z=12 m 处。 Us 为沉降定义的固结度。由图3可见，真空在桩间土中引起负孔压，在持续真空作用下负孔压的数值逐渐增大，最后稳定在约?80 kPa。由解析解得到的复合地基固结度和桩间土孔压与有限元解的结果十分接近，解析解计算的孔压是桩间土深度 z=12 m 的平均值，数值略大于有限元解。算例证明了本文解析解的合理性。

5 复合地基固结性状分析

现通过单参数分析法来研究真空下钉形搅拌桩复合地基的固结特性。用作比较基准的参数如下： H=16 m ， H1=4 m ， H2=12 m ， rg1=0.5 m， rg2=0.25 m，re=1.2 m，m=0.04，ρ=2。Es1=Es2=3 MPa， kv1=kv2=10?7 cm/s，桩的压缩模量 Ep1=Ep2=Ep=120 MPa ，q（t）=80[1?exp（?t）]。

图4给出了不同扩大头半径情况下复合地基的固结度曲线，扩大头半径 rg1=0.3，0.4，0.5，0.6 m ，相应的扩大头的扩径比ρ=1.2～2.4。从图4中可以看出，在固结前期复合地基的固结速率随扩大头半径的增加而略微增大，在固结后期则随扩大头半径的增加而减小，但减小的幅度非常小。

图5给出了不同扩大头高度情况下复合地基固结速率曲线的比较，扩大头高度 H1=2，4，6，8，10 m。从图5中可以看出，真空下钉形搅拌桩复合地基固结速率随扩大头高度的增加而增大，在固结中期较为显著，这与杨涛等[14]指出的荷载作用下复合地基固结速率随扩大头高度的增加先略微减小然后增大有所不同，这主要是真空下桩间土是负孔压下固结，负压下桩?土间相互作用机制与荷载下不同引起的。

图6给出了小直径搅拌桩的置换率 m 对复合地基固结速率影响曲线图， m=0.04，0.05，0.08，0.1，计算中桩的几何尺寸不变。 m 增加表示整个钉形搅拌桩的置换率增大。从图6可以发现，复合地基的固结速率随着钉形搅拌桩置换率的增加而增大，但增加的幅度逐渐减小。

图7给出了下层桩间土与上层桩间土的压缩模量之比 Es2/Es1对复合地基固结度的影响，Es2/Es1=1.0，3.0，5.0，7.0，9.0，计算中 Es1的数值保持不变。 Es2/Es1数值增加，扩大头以下桩间土的刚度随之增大。图7的计算结果表明，扩大头以下桩间土的压缩模量越大，复合地基的固结越快，但固结速率的增幅逐渐减小。

图8给出了真空加载参数α对复合地基固结速率的影响。从图8中可以看出，不同α下复合地基固结度曲线近乎重合，说明真空加载参数α对钉形搅拌桩复合地基固结速率的影响很小。

6 结 论

建立了真空下钉形搅拌桩复合地基固结解析解，并对复合地基的固结特性进行分析，主要结论如下：

a.在固结早期，钉形搅拌桩复合地基的固结速率随扩大头半径的增加而增大，但在固结后期，扩大头半径的变化对复合地基固结的影响较小。

b.增加钉形搅拌桩置换率、扩大头的高度和它下面桩间土的压缩模量，钉形搅拌桩复合地基的固结速率增大。

c.真空加载过程对钉形搅拌桩复合地基固结的影响较小。

参考文献：

[1] ZHANG Z， YE G B， XU Y. Comparative analysis on performance of vertical drain improved clay deposit under vacuum or surcharge loading[J]. Geotextiles  and Geomembranes， 2018， 46（2）：146–154.

[2] WU J， XUAN Y J， DENG Y F， et al. Combined vacuum and surcharge preloading method to improve Lianyungang soft marine clay for embankment widening project： a case[J]. Geotextiles and Geomembranes， 2021， 49（2）：452–465.

[3] ALMEIDA M S S， DEOTTI L O G， ALMEIDA M C F， et al. Vacuum preloading on structured clay： field， laboratory， and numerical studies[J]. International Journal of Geomechanics， 2021， 21（10）：04021198.

[4] INDRARATNA  B，  RUJIKIATKAMJORN  C， SATHANANTHAN I. Analytical and numerical solutions for a single vertical drain including the effects of vacuum preloading[J]. Canadian Geotechnical Journal， 2005， 42（4）：994–1014.

[5]韩文君， 刘松玉， 章定文， 等.基于双对数压缩模型的真空预压非线性固结解[J].东南大学学报（自然科学版）， 2013， 43（5）：967–972.

[6]张玉国， 万东阳， 郑言林， 等.考虑径向渗透系数变化的真空预压竖井地基固结解析解[J].岩土力学 ， 2019， 40（9）：3533–3541.

[7]郭彪 ， 龚晓南 ， 卢萌盟 ， 等.真空联合堆载预压下竖井地基固结解析解[J].岩土工程学报 ， 2013， 35（6）：1045–1054.

[8]林伟岸， 江文豪， 詹良通.考虑真空加载过程及堆载随时间变化下砂井地基的普遍固结解析解[J].岩土力学 ，2021， 42（7）：1828–1838.

[9]田乙， 吴文兵， 张霖， 等.堆载?真空联合预压下的未打穿竖井地基固结理论[J].岩土工程学报 ， 2022， 44（3）：533–540.

[10]叶观宝， 张晴雯， 张振.真空联合堆载预压下混凝土芯砂石桩复合地基固结特性理论分析[J].岩土力学 ， 2016，37（12）：3356–3364.

[11]张丹贝， 张玉国， 黄彤， 等.真空预压条件下未打穿不排水桩复合地基一维固结研究[J].工业建筑， 2018， 48（5）：118–121.

[12]张玉国， 杨晗玥， 段萌萌， 等.真空?堆载联合预压条件下复合地基固结解析解[J].长江科学院院报， 2019， 36（5）：75–80.

[13]张玉国， 段萌萌， 杨晗玥， 等.真空?堆载联合预压复合地基径向固结理论研究[J].地下空间与工程学报 ， 2020， 16（6）：1729–1736.

[14]杨涛， 盛志成， 王恒栋.钉形水泥搅拌桩复合地基一维固结解析解[J].工业建筑， 2020， 50（3）：102–108.

[15]杨涛， 盛志成.变荷载下悬浮 TDM 桩复合地基固结分析[J].中国公路学报， 2020， 33（9）：76–84.

[16]谢康和.双层地基一维固结理论与应用[J].岩土工程学报， 1994， 16（5）：24–35.

[17] CHU J， YAN S W. Estimation of degree of consolidation for vacuum preloading projects[J]. International Journal of Geomechanics， 2005， 5（2）：158–165.

[18]彭劼， 董江平， 宋恩潤， 等.考虑加载过程的真空预压轴对称解析解[J].岩土力学， 2010， 31（S1）：79–85.

（编辑：石 瑛）