基于IPSO-SVR的盾构下穿既有道路沉降预测分析

魏海斌 魏东升 蒋博宇 马子鹏 刘佳佳

（1.吉林大学 交通学院，吉林 长春 130000；2.中铁二十二局集团轨道工程有限公司，北京 100043）

随着轨道交通网络的不断发展，不可避免地产生下穿既有道路现象［1］，而在盾构施工的过程中，土体扰动与地下水文条件变更等无疑会造成路表的沉降变形［2］，影响道路质量及盾构施工进度。因此，建立准确度较高的机器学习模型以预测盾构施工中沉降的变化规律，对道路运营与施工安全有着至关重要的作用。

在现行的盾构下穿所产生的沉降影响研究中，难以建立出盾构参数与地面沉降之间的非线性关系表达式［3-4］，故在进行盾构参数优化的过程中也就难以确定准确的目标函数，较多学者采用理论模型与现场数据监测来合理进行沉降分析。Luo等［5］基于Biot固结理论，建立了三维流-土体全耦合数学模型，预测盾构隧道施工引起的孔隙水压力变化和地面沉降。岳迎新［6］通过FLAC3D建立有关隧道施工的仿真模型，采用Peck公式分析盾构过程中路面沉降预测。张运强等［7］在Peck公式基础上提出盾构隧道施工诱发地面三维沉降的计算公式，合理预测地层沉降情况。Deng等［8］通过理论分析和动态监测方法优化盾构施工参数，研究表明对沉降的控制良好。

近些年，较多学者将机器学习方法应用于盾构施工产生沉降规律研究中。在国内，孙钧等［9］首次进行人工智能神经网络地面沉降预测研究，结合上海地铁工程，预测盾构前方5 m地面沉降，与现场实测值较为一致。张碧文等［10］通过灰色模型（GM）算法，发现地铁盾构施工下高铁路基已有沉降数据之间的规律，进而预测后续沉降。随着计算机科学技术发展，更多学者将机器学习与优化算法相结合，通过合理优化学习模型来有效降低沉降预测中出现的误差。刘育林［11］建立麻雀搜索算法优化支持向量机回归（SSA-SVR）预测模型，对煤矸石路基沉降进行预测。陈伟航等［12］基于双向长短期记忆网络（Bi-LSTM），结合滚动迭代方法后延更新沉降预测，可有效提升路基沉降预测可靠性。周中等［13］采用遗传算法优化双向长短期记忆网络（GA-Bi-LSTM），为盾构平行下穿既有隧道沉降进行预测，通过对比分析表明其拥有更好的预测精度。Hou等［14］采用支持向量机（SVM）训练好的模型，利用指数调整惯性权重优化免疫粒子群对隧道掘进参数进行调整，在样本不断减少的情况下仍能保持高度准确性。Zhu等［15］应用间隙参数（GP）模型，建立了西安地铁二号线地面沉降的修正预测方法。

现有多数研究集中在盾构隧道下穿既有道路、铁路或隧道沉降预测与控制方面，对于长距离平行既有道路的沉降预测研究相对较少。本研究依托长春地铁6号线实际工程，以盾构施工掘进参数、地层信息及沉降实测为研究对象，通过改进粒子群算法优化支持向量回归（IPSO-SVR）模型预测上部平行道路的沉降情况。基于已有研究和Sobol敏感性分析确定沉降影响输入参数，结合网格搜索法与非线性递减策略改进粒子群优化算法，以搜寻SVR最佳超参数，确定出盾构多因素影响下道路变形沉降的预测模型，并进一步提高收敛速度与预测精度。

1 改进粒子群算法优化的支持向量回归预测模型

1.1 支持向量回归理论

Cortes等［16］最早提出基于统计学习理论发展的SVM算法，可完美兼顾样本信息冗杂性与学习性能，在规避局部最小值、优化网络结构、提高收敛速度和缩减训练样本量等方面有更好表现。而作为将其应用于回归的支持向量回归（SVR），就是通过优化训练学习，通过寻求最佳分类面使得训练样本到该分类面的偏差最小，引入不敏感损失函数，以获取较好的回归效果。

首先，定义n个训练集样本（xi，yi），i=1，2，…，n，xi为输入参数，yi为对应的输出值，均由真实测试获取。在高维特征空间中，构建分类超平面或逼近函数进行回归：

式中：f（x）为目标函数值，x=［x1，x2，…，xn］，为输入值；wT是线性权重向量；φ(x)为映射函数，可以有效解决非线性回归问题；b为截距。

通过引入松弛因子ξi和ξ＇i，求解最优值的问题可以转化为

其中：

式中：C为惩罚因子，体现对训练误差大于ε的样本惩罚程度；ε为损失函数参数，代表回归函数的误差程度。

引入Lagrange乘子αi和α＇i，ηi和η＇i，且αi，α＇i，ηi，η＇i≥0，将上式转换为

为求w、b、ξi、ξ＇i最小与αi和α＇i最大，对参数求取偏导数，得到如下对偶形式：

其中K(xi，xj)=φ(xi)φ(xj)为满足对称性和正定性的核函数，通过Karush-Kuhn-Tucker条件，得到b的值为

最终进行预测的非线性模型即确定为

式中，ˉ为计算得出的b平均值。

1.2 粒子群优化算法

粒子群优化算法（PSO）最先由Eberhart等［17］提出，作为一种全局优化算法，其利用粒子间相互协作来实现对整个群体信息的共享，以在其中寻求最优解。

PSO算法可以理解为：初始化粒子群的位置与速度，通过不断迭代更新个体粒子位置与速度向量，并引入适应度函数，比较粒子局部与全局适应度值，评选出个体极值，同时利用局部最优值与全局最优值进行比较，评选最优群体极值。通过不断更新个体极值和群体极值，最后当算法寻求到适应度最优解或者达到最大迭代次数时结束计算［18-19］。

其中各个粒子更新位置和速度的函数如下：

式中，ω为惯性权重，k为粒子群迭代数，V为粒子群速度，χ为粒子群位置，pbset为个体极值，gbest为群体极值，c1、c2为学习因子，r1、r2为［0，1］随机数。

1.3 基于改进粒子群算法的支持向量回归优化

在目前研究中，机器学习算法模型性能优化的关键在于寻找最优超参数，传统方法以人工试错为主，这种方式不仅耗时较长，也难以找到最优解［20］。为有效提高模型预测性能，有较多学者采用PSO对预测模型进行优化，与其他算法相比PSO具有最好的优化性能，不过容易陷入局部极值并且收敛速度与寻优能力受到惯性权重和学习因子影响［21］。因此，本研究设计采用一种改进粒子优化算法，通过网格搜索法缩小SVR中超参数范围［22］，并结合非线性递减策略不断更新PSO的惯性权重与学习因子［23］，有效避免超参数搜寻过程中陷入局部极值并提高收敛速度，从而最大程度减小SVR预测误差。基于上述的优化方法与步骤，建立IPSO-SVR预测模型，流程如图1所示。

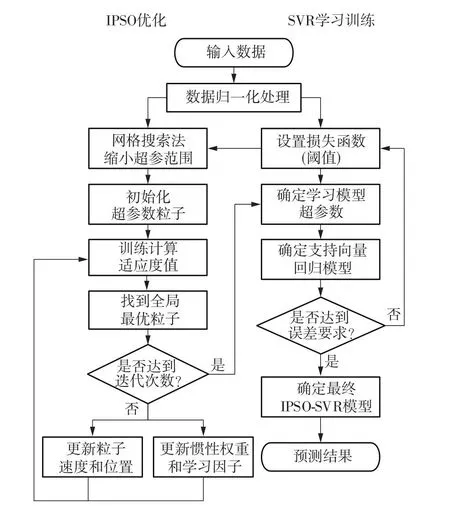
图1 IPSO-SVR模型预测流程Fig.1 IPSO-SVR model prediction process

2 IPSO-SVR沉降预测输入参数的选取

现有研究发现，由于实际盾构施工中无法实现单一变量控制，地表沉降与各独立参数并无绝对明确关系，而是受多因素参数耦合作用影响。因而，正确找到影响沉降最为关联的输入参数对提高模型的准确性与可行性有重要作用。基于此目标，本研究从几何因素、地质因素与盾构掘进因素三方面来确定影响道路沉降的输入参数。

2.1 几何参数

作为隧道重要的几何因素，隧道埋深与直径对地表沉降有较大的影响。在进行道路沉降影响分析时选用深跨比（埋深H/直径D）作为几何参数，在基于单个工程的机器学习算法研究中，D基本不发生改变，而随着H的增加，地表竖向位移逐渐减小。

2.2 地质参数

盾构区地层性质同样影响掘进过程中的地层扰动，地层的物理力学性质差异会导致对地表沉降的不同影响［24］。结合纵断面地质构造与勘察结果，选取地下水位埋深作为水文构造影响参数。在地层强度参数分析中，结合本工程实际试验发现，盾构机掌子面土体的压缩模量、泊松比与孔隙比变化很小，反映在其对沉降的影响较小。因而采用变化较大的粘聚力、内摩擦角及侧压力系数按照厚度加权作为地层强度参数。

2.3 盾构掘进参数

盾构掘进参数种类众多，其中注浆压力、注浆量、盾构推力、盾构姿态、土仓压力及掘进速度等是影响地层沉降变形的重要因素［25］。虽然大多数盾构掘进参数在一定程度上都能反映对地表沉降的影响，但输入参数过多、维度过高会导致模型难以收敛，影响训练效果。

因此，本研究以Sobol敏感性分析［26-27］讨论盾构掘进参数对道路沉降影响的关联性，选取相应的主要参数。根据参数变量的取值范围，采用蒙特卡洛法采样并进行关联性计算，得到各盾构参数的一阶影响指数和全局影响指数，如表1所示。

表1 各盾构参数对最终沉降的影响程度Table 1 Affect degree of each shield parameter on the final settlement

在本次工程盾构掘进参数对道路沉降的全局影响比较分析中可以发现，同步注浆量、盾构推力、土方重、刀盘扭矩及土仓压力对地表道路沉降的影响贡献较大，而注浆压力与贯入度相对较小。因此，本次选取全局影响指数大于0.1的参数作为影响道路沉降的主要盾构掘进参数。

3 工程实际应用分析

本研究位于长春地铁6号线2号标段飞跃广场站-欧亚卖场站上行线盾构区间（ZK16+197.489～ZK 17+575.235），短链5.299 m，区间长1 372.44 m。线路最小曲线半径为550 m，线路最大坡度为13.268‰，隧道顶部覆8.7～12.3 m。如图2所示，线路向东南方向敷设，下穿雨污水管线、燃气管线、飞跃路、专用线、京哈铁路。本区间重难点在于长距离平行下穿飞跃路的沉降变形控制问题。

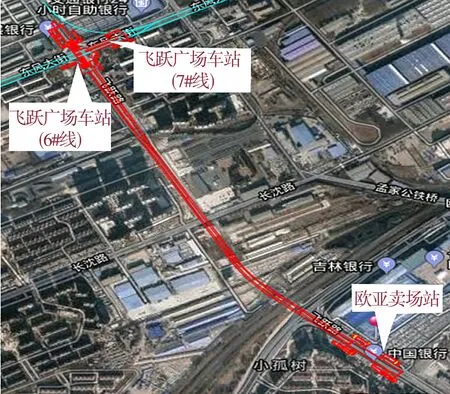
图2 区间地理位置Fig.2 Interval geographic location

3.1 地质概况

本区间工程地质单元地形起伏平坦，地貌类型为冲积洪积波状台地。如图3所示，盾构隧道主要穿越地层为全风化泥岩层、强风化泥岩层、中风化泥岩层，上部覆填土层与粉质粘土层，主要地质参数见表2。初勘阶段共观测一层地下水，水位埋深1.2～9.2 m，含水层主要为粉质粘土层，主要接受侧向径流及越流补给。

表2 区间地层力学性质及特殊指标Table 2 Mechanical properties and special indicators of interval strata

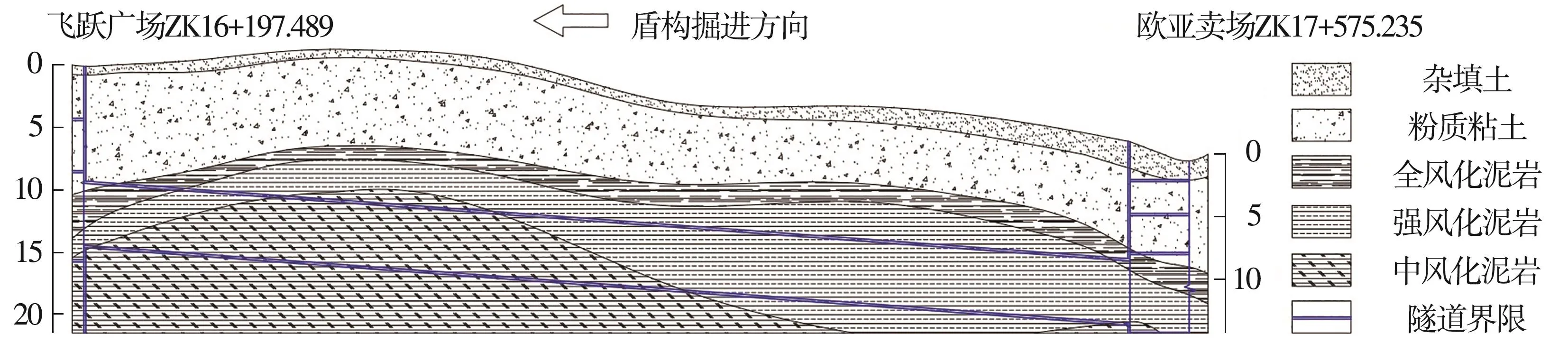
图3 ZK16+197.489～ZK17+575.235地质纵断面（单位：m）Fig.3 Geological longitudinal section of ZK16+197.489～ZK17+575.235（Unit：m）

3.2 样本选取

在上行线平行既有道路区间内，选取250环（ZK17+200.235）至545环（K16+757.735）间隔5环进行样本数据采集，其中几何参数与地层参数按勘测结果经计算调整获取，盾构掘进参数在盾构施工系统实时记录监测，道路沉降则采用工后固结的路表最大沉降值，最终确定出60组数据，形成包含10个输入参数与1个输出参数的样本集合。随机选取其中48组采集数据作为样本训练集，进行模型训练；选取剩余12组采集数据作为测试集，以分析预测模型的精确程度与有效性，部分代表数据如表3所示。

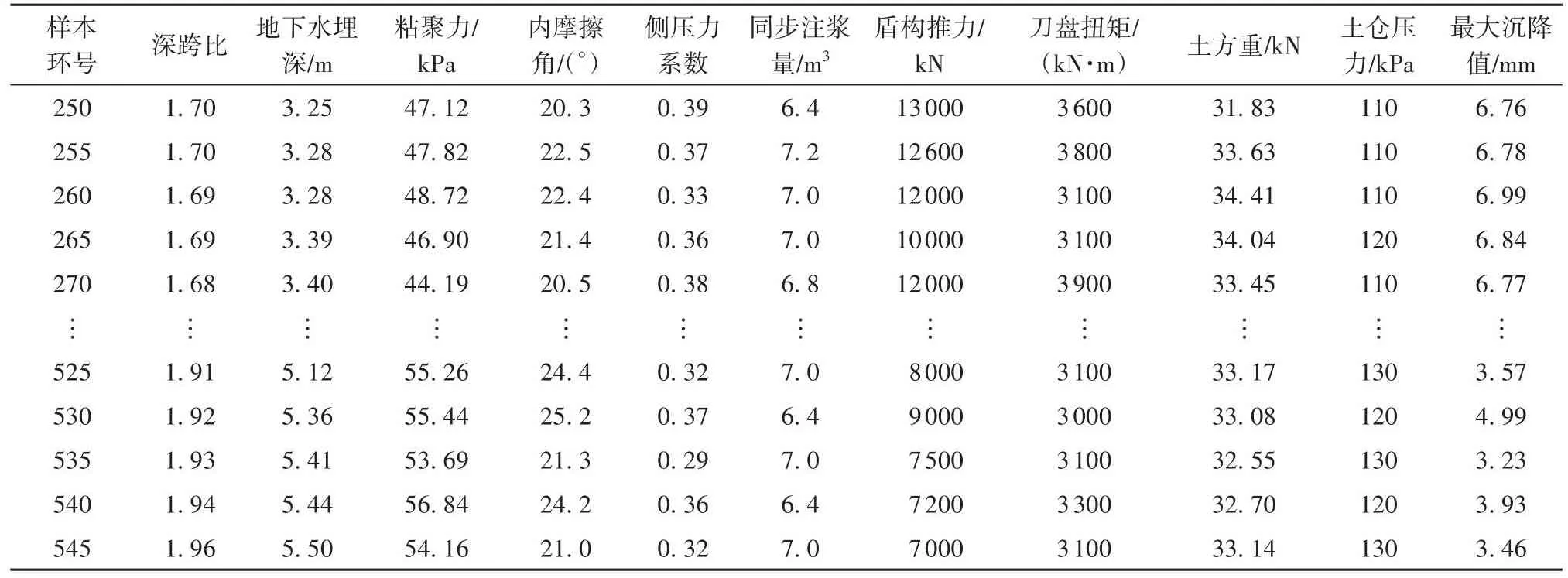
表3 沉降预测模型的部分训练样本参数Table 3 Part training sample parameters of sedimentation prediction model

3.3 多因素耦合作用下的IPSO-SVR盾构施工道路沉降预测

样本参数间有着不同的量纲与量纲单位，取值范围相差悬殊，如果直接进行模型训练会导致取值范围大的参数影响效果显著，模型精度因此受到影响。因此，为求得最优解提高模型预测精度，对数据进行最值归一化处理，使之映射到［-1，1］之间，计算如下：

式中，x＇为归一化后的数据，x为初始样本数据，xmin为对应参数数据的最小值，xmax为最大值。

结合网格搜索法缩小超参数范围。将超参数C、γ在［2-10，210］间隔20.5取值进行排列组合，列出所有可能的组合结果生成“网格”，将各组合用于模型训练，并使用10折交叉验证对表现进行评估。引入目标函数（均方误差），最优解即为目标函数最小值，依靠支持向量机库（libsvm［22］-3.25）中的网格搜索法及SVR得到目标函数结果。如图4所示，发现C、γ在［2-10，210］有多个局部极值（其中最小目标函数值为0.046 7，C=2，γ=0.125），这使PSO在短期内可能难以找到最佳结果。基于此原因，结合图4缩小搜寻范围至C、γ分别为［20，210］和［2-5，20］。

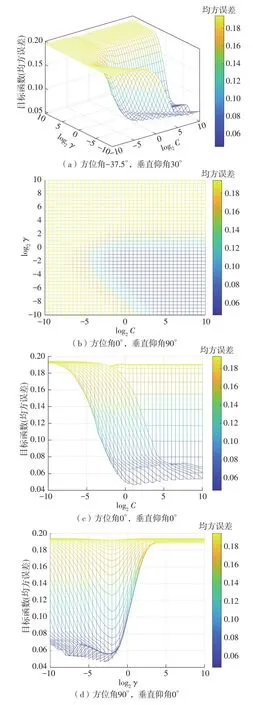
图4 超参数C、γ对应的目标函数变化Fig.4 Hyperparameter C， γ corresponding to the object function change

在缩小的范围内仍不可避免地存在局部极值，基于PSO中惯性权重ω与加速因子c1、c2寻优影响特点，当惯性权重因子和加速因子较大时，其全局寻优能力较好；若惯性权重因子和加速因子较小，则其局部寻优能力较好［23］。为增强算法寻优能力采用非线性递减策略，使惯性权重ω与加速因子c1、c2由固定不变改进为非线性的速度变化，对其具体改进如下：

式中：λ为非线性系数，本文取0.45；t为当前迭代次数；m为最大迭代次数；c1max、c1min分别代表c1的最大值和最小值，取2.0和0.1；c2max、c2min分别代表c2的最大值和最小值，取2.0和0.1。

在SVR的核函数K(xi，xj)选择中，相较于多项式与Sigmoid核函数，在大部分数据处理中径向基函数（RBF）具有更好的预测效果［28］，因此本研究采用RBF作为核函数。通过上述IPSO改进进行SVR超参数优化，选取粒子群规模为30，粒子维度为超参数个数，最大迭代次数选取400，交叉验证次数取10，损失函数设置为0.01。对比相同条件的PSO（其中参数c1=1.5，c2=1.5，ω=0.8）的目标函数变化，如图5所示。

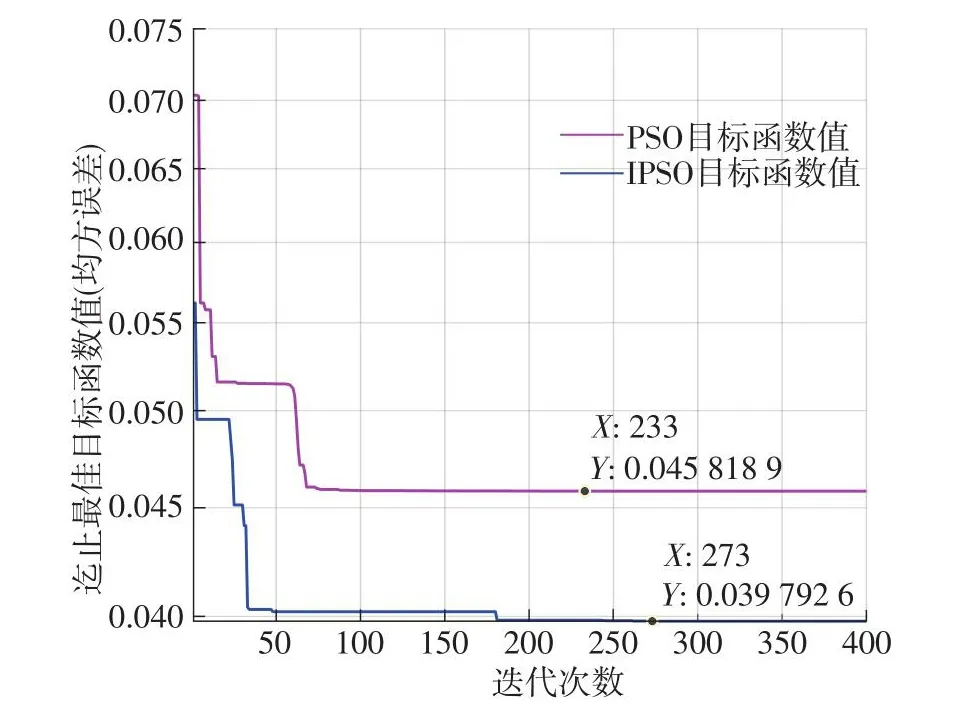
图5 道路沉降预测目标函数变化曲线Fig.5 Change curves of road settlement prediction object function

从图5中可以看出，相较于PSO目标函数变化情况，IPSO收敛速度有明显提升，并且收敛效果更好。PSO迭代到233次时达到最小，应对目标函数值为0.045 8（C=2.034 9，γ=0.140 3）；随着IPSO迭代次数增加到273次，目标函数达到最小值0.039 8（C=16.158 4，γ=0.055 7），表明此时预测值与实际值最为接近，依据最小目标函数值对应SVR超参数进行预测分析。

3.4 模型预测结果分析

为验证模型预测能力，采用平均绝对误差（MAE，即EMA）与拟合决定系数R2作为IPSO-SVR预测模型的评价指标，其计算公式分别如下：

式中，n为数据样本数量，f(xi)为道路沉降预测值，yi为道路沉降实测值。MAE越小则说明模型性能越好，R2结果区间为［0，1］，越接近1拟合度越高，预测效果则越好。

为增加模型评估可信度，采用反向传播（BP）神经网络、支持向量回归（SVR）、粒子群优化的支持向量回归（PSO-SVR）3种模型与IPSO-SVR预测模型进行对比分析。其中，对比模型的输入参数、输出参数及训练次数均与IPSO-SVR保持一致，采用tansig-tansig传递函数与trainlm训练函数［29］通过多次试验验证确定预测效果较好的BP模型，在SVR与PSO-SVR中则以K折交叉验证结果或经验公式确定参数，最终确定各对比模型超参数取值如表4所示。

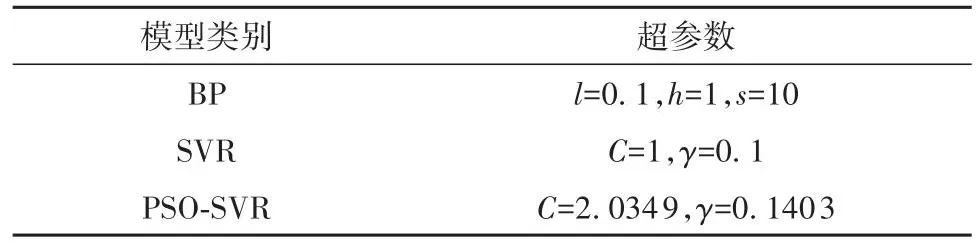
表4 模型超参数的对比1）Table4 Comparison of the model hyperparameters

确定各模型结构参数，利用训练集对模型进行训练，对全体样本进行预测分析，得到各模型预测结果与评价指标如图6-图9所示。

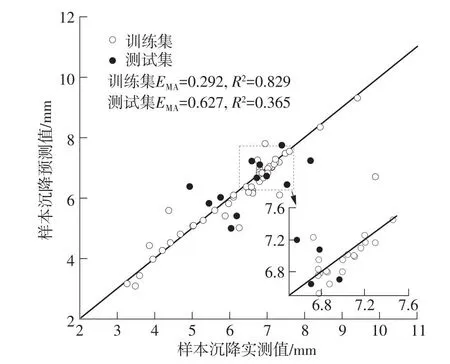
图6 BP模型预测结果与评价指标Fig.6 Prediction results and evaluation indicators of BP model

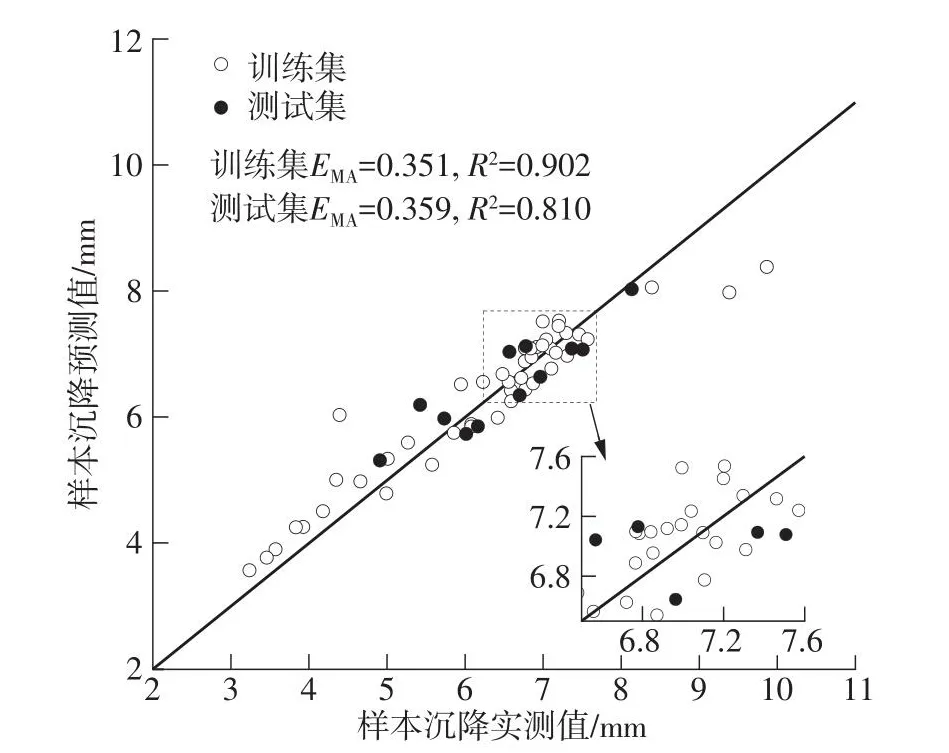
图7 SVR模型预测结果与评价指标Fig.7 Prediction results and evaluation indicators of SVR model

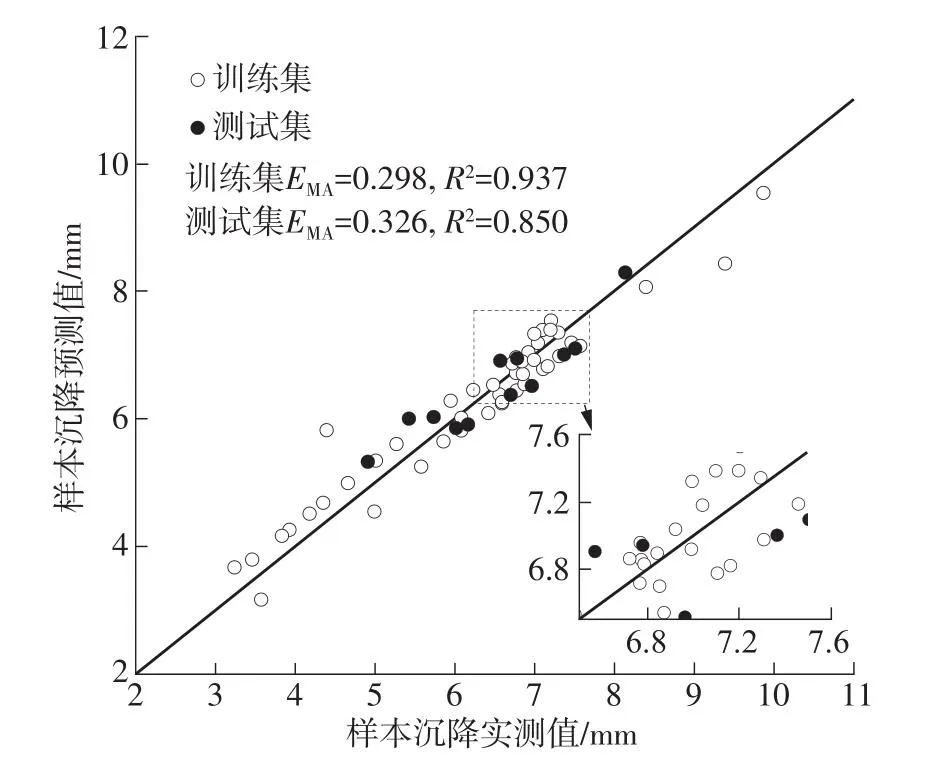
图8 PSO-SVR模型预测结果与评价指标Fig.8 Prediction results and evaluation indicators of PSOSVR model

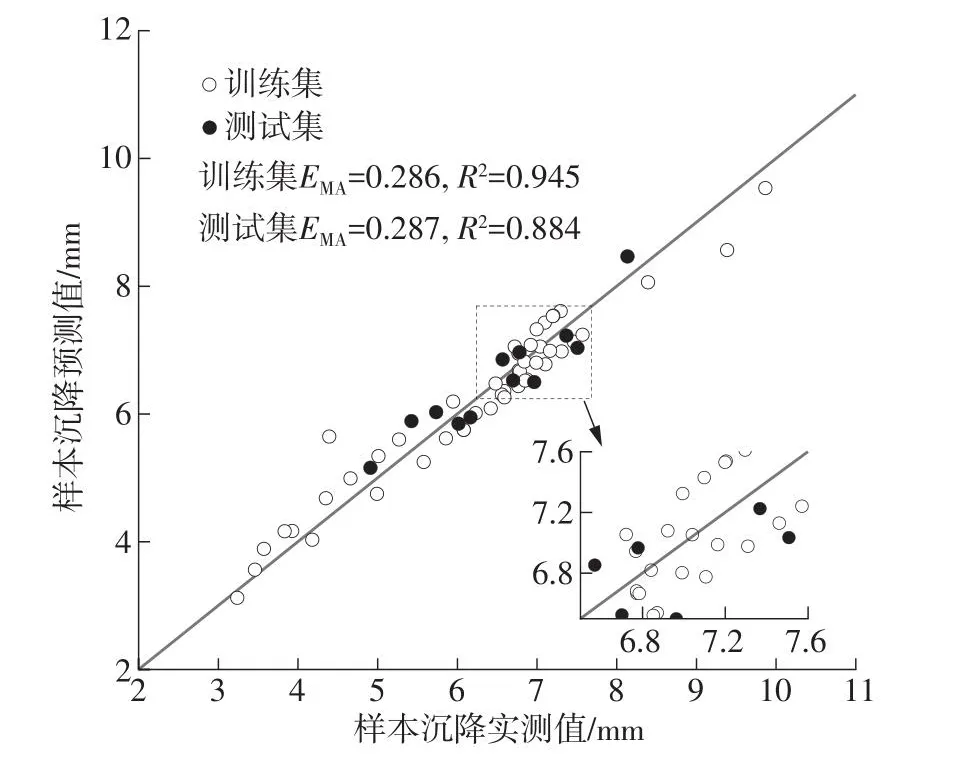
图9 IPSO-SVR模型预测结果与评价指标Fig.9 Prediction results and evaluation indicators of IPSOSVR model

在图6-图9中可以发现，BP模型中训练集样本点较多集中在对角线上，说明模型在训练中过度拟合，由此导致测试集预测效果不佳，部分样本出现较大误差，训练集的评价指标产生较大差异；在SVR、PSO-SVR与IPSO-SVR中，预测输出结果稳定，训练集与测试集指标均表现良好且无明显差异。预测结果说明，盾构施工中掘进参数与地层信息等因素与既有平行道路沉降存在内在联系，并且在输入参数的选择较为合理时模型均能进行有效预测。在所有模型测试集的对比中，IPSO-SVR表现最佳，测试集MAE为0.287，R2为0.884，具有最为优秀的预测精度与拟合优度，在盾构施工影响既有道路沉降中能够表现出更为准确可信的预测效果。

为使预测可靠性更加显著，将模型测试结果进行对比分析，测试集沉降预测值与相对误差结果如图10-图11和表5所示。

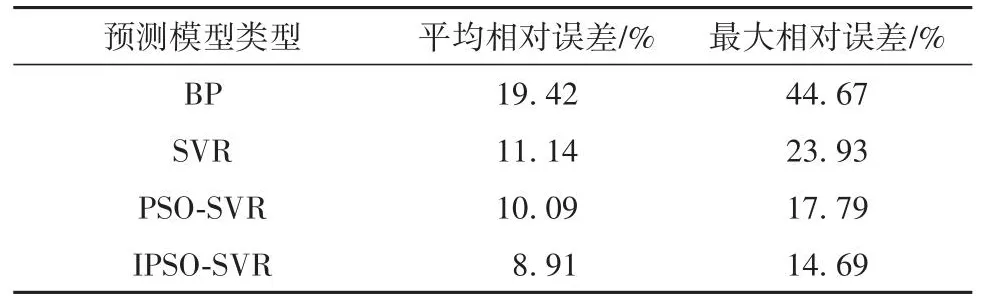
表5 不同预测模型结果误差Table 5 Errors in the results of different predictive models

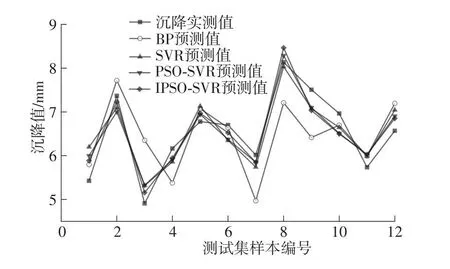
图10 各模型测试集沉降预测结果Fig.10 Settlement prediction results for each model test set

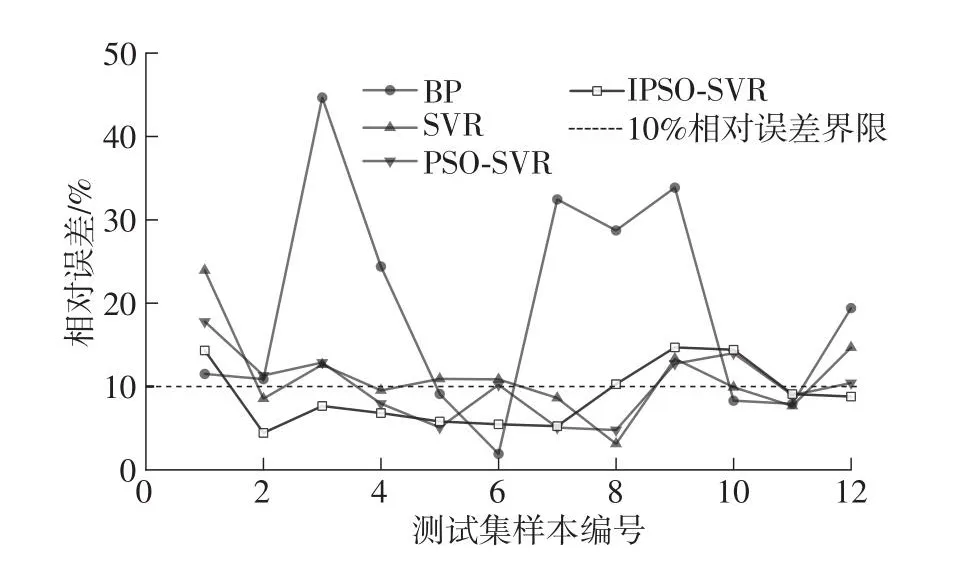
图11 各模型测试集沉降预测相对误差Fig.11 Relative errors of settlement prediction for each model test set

由图11可以看出，4种预测模型测试所得到的沉降预测相对误差保持在20%以内，最大相对误差均小于50%，均有较好表现。相较于BP、SVR与PSO-SVR中10%～20%的平均相对误差，IPSO-SVR将其缩小至8.91%，其中超过70%样本预测误差控制在10%以内，而在其他模型中满足这一标准的尚未超过50%。由此可见，本研究所构建的IPSOSVR模型沉降预测更加贴近实际测量值，在预测精度与误差稳定性方面都有更好表现。

4 结语

本研究采用网格搜索法与非线性递减策略改进粒子优化算法优化SVR超参数，结合长春地铁6号线复杂地质条件，综合考虑盾构施工区间多因素耦合条件对既有平行道路的沉降影响，依靠libsvm-3.25建立IPSO-SVR既有道路沉降模型，并与PSOSVR、SVR、BP 3种模型进行沉降预测对比，研究结论如下：

（1）IPSO-SVR、PSO-SVR、SVR以及BP 4种预测模型所得到的沉降预测相对误差均保持在20%以内，最大相对误差小于50%，在既有道路沉降预测中均具有较好表现，说明本研究选取的掘进参数与地层信息等作为影响参数较为合理，符合实际盾构过程中道路沉降的施工影响情况。

（2）对比发现PSO-SVR预测结果较好于SVR与BP，但在进行粒子群迭代过程中有收敛慢、易陷入局部最小值的明显缺陷，本研究提出的IPSOSVR可以很好避免此现象发生。

（3）与BP、SVR、PSO-SVR相比，本研究所提出的IPSO-SVR测试结果中MAE为0.287，R2为0.884，平均相对误差控制在10%以内，其预测效果与拟合程度最佳。

本研究建立IPSO-SVR模型并根据相应参数和已有沉降数据，预测施工过程中既有道路沉降并对现场掘进参数进行反馈调整，可为道路沉降控制提供可靠依据。IPSO-SVR可实现复杂情况下较小样本量多因素作用的非线性预测，其模型与方法具有可行性与泛化性，其开发一定程度上依赖于超参数优化，而“黑箱”属性使得智能模型解释性不佳，需根据实际工程而应用，本文建立模型的思路可为其他领域的预测模型的建立提供一定借鉴。