考虑侧向车换道影响的理论和数据组合驱动的车辆跟驰模型

赵建东 焦岚馨 赵志敏 屈云超 孙会君

（1.北京交通大学 交通运输学院，北京 100044；2.北京交通大学 综合交通运输大数据应用技术交通运输行业重点实验室，北京 100044；3.北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044）

跟驰和换道是两种常见的车辆驾驶行为，车辆正常行驶过程中，仅受前方车辆的交通状态影响，然而当其侧方车辆发生换道行为时，出于驾驶安全性考虑，正常行驶车辆的状态会受到侧方车辆交通状态的影响。针对这一现象，有效研究侧方车辆换道对正常跟驰行驶车辆的影响，对于分析车辆微观交通行为和提升道路交通安全具有重要意义。

跟驰模型分为传统理论跟驰模型和数据驱动跟驰模型。理论模型具有明确物理意义和严格的推导过程。但是由于道路条件、车辆特性、环境条件等各种复杂条件影响，很难在当前模型结构的基础上进一步提高模型预测的精度，其验证方法多采用仿真数据进行验证，考虑情况有限。数据驱动方法拟合精度高，预测效果好，但数据驱动跟驰模型的研究仅停留在单车道跟驰模型，未考虑侧向车辆换道对目标车辆的影响情况。

在理论跟驰模型方面，Bando等［1］提出一个简单的优化速度（OV）跟驰模型，仅考虑了车间距对驾驶员的影响；Helbing等［2］考虑负速度差影响，提出广义力（GF）模型，引入速度差影响因素；Jiang等［3］在GF模型基础上考虑正速度差影响，提出全速度差（FVD）模型，即当前车比本车快得多时，即使车间距小于安全间距，驾驶员也不会减速；王涛等［4］考虑到非邻近车辆的速度信息对交通流的影响，考虑了多辆前车速度差的影响作用，在FVD的基础上提出了FVD模型的扩展模型——多速度差（MVD）模型；孙棣华等［5］进一步考虑多前车位置和速度差的共同作用，提出（MAVD）模型。以上研究均为单车道跟驰模型，未完全考虑换道车辆的汇入对模型的影响。近年来，有学者考虑到侧方车辆并线的换道影响，将单车道跟驰模型扩展到双车道模型。Kesting等［6］考虑横向车辆的影响，提出双车道下的跟驰模型。Tang等［7］认为在双车道交通流中，驾驶员总是担心邻近车道将有换道行为发生，在已有成果上建立了双车道车辆跟驰模型。陈漩等［8］在双车道模型中引入反馈控制信息，发现相对OV扩展的模型能有效抑制交通堵塞。王玄金［9］以NGSIM实测数据为基础，基于FVD模型，分析车辆换道对目标车道以及当前车道后车的影响，分别建立换道汇入和换道穿越两种理论跟驰模型。刘大为等［10］分析车辆在跟驰状态下行驶时的影响因素，考虑驾驶员心理因素，在优化速度模型基础上结合侧向车辆影响建立新跟驰模型。陶鹏飞［11］从全新的角度出发，将车辆行驶过程中加速度的变化抽象为“力”对车辆的作用，建立跟驰行为模型。

在数据驱动跟驰模型方面，周立军等［12］开发了基于粒子群优化（PSO）算法的人工神经网络算法，建立了车辆跟驰模型，该模型相比传统模型具有更强的鲁棒性。Xiao等［13］利用长短期记忆网络（LSTM）学习车辆跟驰行为。Huang等［14］建立基于LSTM的跟驰模型，研究非对称驾驶行为中的时滞现象和不完美驾驶行为。王梦玉［15］考虑不同城市道路类型、天气以及时段因素，利用实际车车通信环境下的车辆跟驰行驶数据，提出了一种基于LSTM网络的车辆跟驰模型，预测后车速度和车头间距2个参数。Yang等［16］在传统的基于LSTM的跟驰模型的基础上进行了两项改进。在训练过程中使用了一种定时采样技术来解决误差在时间维度上的传播问题。还开发了一个单向互联的LSTM模型结构，以提取轨迹特征。孙倩等［17］考虑驾驶员不确定性和记忆效应，提出基于长短期记忆（LSTM）网络的车辆跟驰模型并进行验证，仿真研究驾驶员记忆效应影响时长。

多数研究都是仅考虑单车道前车的情况，然而在实际的驾驶情况中，驾驶员往往并不只是紧跟前车，仅受前车的影响，而是会保持较大的车距，还受侧向换道车辆驾驶状态的影响，当侧向车辆发生换道情况时，车辆运行状况必然改变。关于侧向车辆影响的跟驰模型还停留在理论层面，对实际交通数据预测准确性相对不够高。本研究以受前向和侧向车辆影响的多速度差理论模型为基础，构建CNNBi-LSTM-Attention数据驱动深度学习模型，并将二者以最优加权法进行组合，建立受侧方换道影响的理论-数据组合跟驰模型并以实际数据进行验证。

1 侧向车辆影响下的跟驰模型的建立

1.1 换道影响行为分析与理论建模

仅有前后跟驰行为时，驾驶员根据前车行为调整交通状态，以维持安全稳定的跟驰过程。当周围车辆发生换道行为时，车辆同时受前方车辆和侧方车辆的影响。本文针对图1所示的侧方相邻车辆换道至本车道（LM）的行为开展研究［9］。

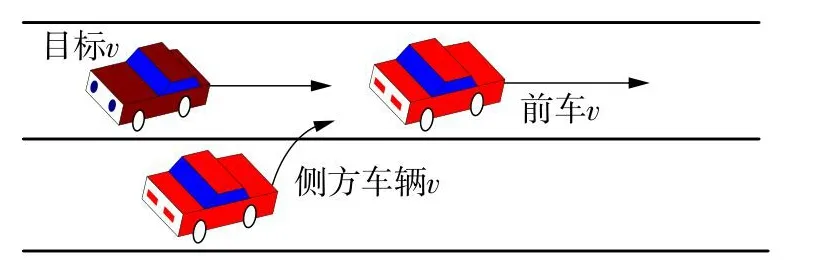
图1 LM换道行为Fig.1 LM lane changing behavior

在理论跟驰模型方面，Jiang等［3］基于正负速度差对跟驰车辆的影响，提出全速度差（FVD）模型：

其中：t表示时间；n表示第n辆车；xn(t)、vn(t)、v̇n(t)分别表示研究车辆的位置、速度和加速度；Δxn(t)和Δvn(t)分别表示和前车的位置差和速度差；λ为速度的敏感系数；a是敏感系数，是驾驶员反应延迟的倒数；V（•）为优化速度函数。

王涛等［4］在此基础上考虑到非邻近车辆的速度信息的影响，考虑了多辆前车速度差的影响作用，提出FVD模型的扩展模型——多速度差（MVD）模型：

其中，L表示前方的车辆数，Δvn+l-1(t)表示和前方第l辆车的速度差。MVD模型通过引入多辆车的速度差来增强车流的稳定性，但没有考虑多辆前车的位置信息。而孙棣华等［5］进一步考虑多辆前车位置和速度差的共同作用，提出（MAVD）模型。

其中，λ为速度差的反应系数，βl和ηl分别为描述前方第l辆车的车头间距和速度差及车型对跟驰车具有不同影响而引入的权重。

MAVD模型考虑了前车位置和速度差信息对跟驰车辆的影响。然而侧方发生换道时，考虑安全性影响，跟驰车辆会极大地受到侧方车辆的位置和速度影响，当侧方车辆距离跟驰车辆很近，跟驰车辆会采取减速让行的行为，当距离较远时，其减速行为较缓慢或者不减速。同样，侧向车辆速度影响也符合全速度差跟驰模型的理论。因此提出关于侧向车辆和前方车辆共同影响的跟驰模型，即FSMAVD模型（Front Vehicles and Side Vehicles & Multiple Ahead & Velocity Difference）：

其中，λ1、λ2为速度差的反应系数，b和c是分别描述前方车辆和侧方车辆的车头间距和速度差对跟驰车的不同影响程度而引入的权重，vn，t代表本车速度，hc为车辆安全距离，vmax为车辆速度最大值，Δx1、Δx2分别为前车和侧向车辆的跟驰间距，Δv1n，t、Δv2n，t分别为前车和侧向车辆的速度差。采用差分进化算法（DE）对理论模型a、b、c、λ1、λ2、hc6个参数进行参数标定。

1.2 数据驱动跟驰模型

基于第1.1节的理论分析，对于LM换道行为，选取前向车辆、侧向车辆以及本车历史状态的6个输入变量，分别为：目标车辆分别与前方、侧方车辆两车的纵向间距，目标车辆分别与前方、侧方车辆两车的速度差，目标车辆速度，目标车辆历史长度T时间内的加速度。输出变量为跟驰车T+1时刻的加速度。根据历史长度T的多变量数据预测T+1时刻的加速度。

构建了一个CNN-Bi-LSTM-Attention数据驱动车辆跟驰模型的神经网络结构（见图2），主要分为输入层、CNN层、Bi-LSTM层、Attention层和输出层。将侧向车辆换道影响的跟驰行为输入数据归一化处理后的数据作为输入层，具体展开结构见式（6）。其中，i表示时刻，j表示输入的不同变量。通过CNN层提取特征，Bi-LSTM层与Attention层从所提取的特征中学习数据内部变化规律以实现预测功能，最后通过输出层得到预测结果。

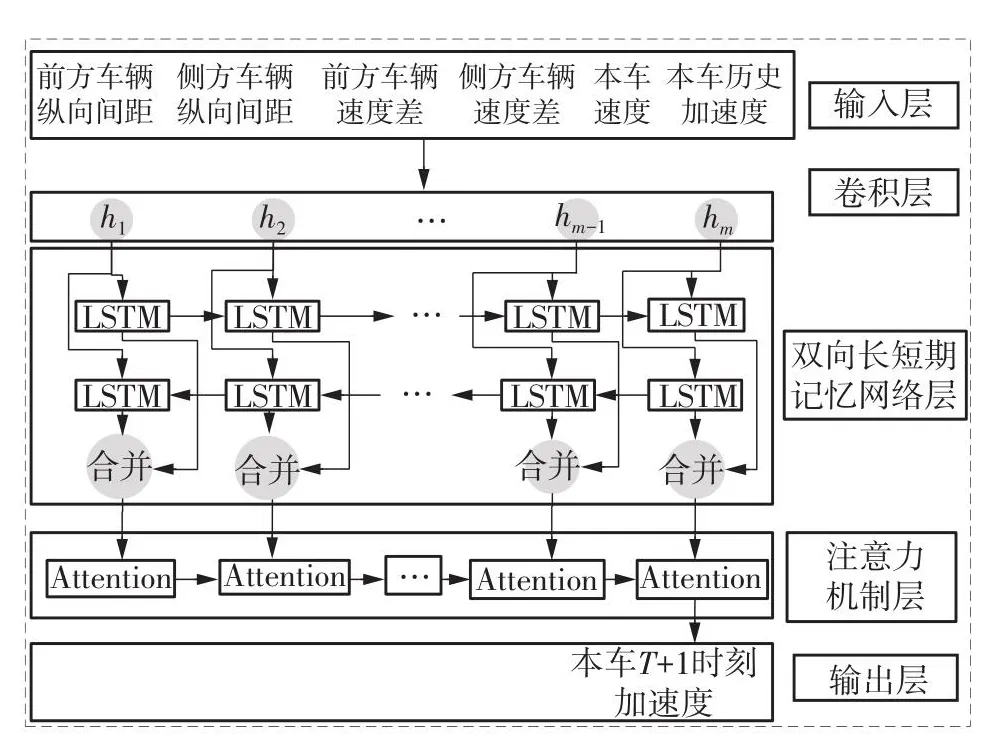
图2 模型结构图Fig.2 Model structure drawing

1）卷积层

在输入数据之后加入一个一维卷积层（1DCNN），选取激活函数。目的是对输入层输入的T×6输入的多维时间序列数据进行特征提取，过滤冗余的信息。并加入随机舍弃层防止过拟合。CNN层输出特征向量表示为

其中，HC表示输出特征向量，W1为权重矩阵，b1为偏差，X为输入层，f为ReLU激活函数。CNN层的输出为

式中，hcm表示行向量，m为CNN层的输出长度。

2）双向长短期记忆网络层

考虑到驾驶员的反应具有记忆性［17］，不只是受当前时刻的周围环境影响，还受历史时刻的交通状态影响。而LSTM神经网络模型具有记忆功能，适用于分析时间序列数据，因此，笔者选用LSTM模型作为核心模型构建双向长短期记忆网络层作为核心预测层。

LSTM内部结构包括输入门、遗忘门和输出门，其中xt表示输入向量。ct和ht表示t时刻记忆细胞状态，σ表示Sigmoid激活函数，tanh为激活函数。其定义如式（9）和（10）所示，分别可以将数据转化为范围（0，1）和［-1，1］的值，其中z为输入变量。

式（11）-（17）分步说明计算过程。其中Wfx、Wfh、Wfc、Wix、Wih、Wic、Wcx、Wch、Wox、Woh、Woc、Who分别为不同变量对应的加权矩阵，bf、bi、bc、bo、bh为其对应的门的偏置。ft、it和ot为门控向量。c͂t为当前输入的单元状态。xt、ht-1为LSTM内部结构中，本结构的输入和上一个连接结构的输出。

遗忘门：

输入门：

输出门：

式中，Ct-1表示t-1时刻传递来的单元状态。

Bi-LSTM模型是两个LSTM模型的组合，一个正向处理序列，一个反向处理序列，处理完后，两个结果以concat方式拼接起来，作为这一层的最终输出。通过提取上一层输入的交通特征数据，并进行有选择的全局学习，能解决LSTM单向运行而导致数据信息利用不充分的问题。

Bi-LSTM层在第t步的输出为

其中，yBi-LSTM表示双向长短期记忆网络层模型的输出结果。

3）注意力机制层

注意力机制（Attention）层是一种模拟人脑的注意力资源分配机制。人脑会在某个特定的时刻将注意力集中在需要重点关注的领域，而忽视其他非重点因素［18］。Attention机制通过概率分配的方式，可以提高模型的准确率。如图2所示，将Bi-LSTM输出的结果输入注意力机制层，再加上Attention注意力机制对不同输入维度特征进行不同的权重分配，决定哪些维对预测维起到关键作用。采用softmax激活函数，计算每个特征的权重。之后是Multiply层，权重乘以输入，得到注意力层的输出。

Attention机制层的权重计算公式为：

式中，et为第t时刻Bi-LSTM的输出向量，hbt为注意力概率分布值，u、w为权重系数，b为偏置系数，αt表示注意力权重分配，s＇t为Attention层在t时刻的输出。

输出层通过全连接层进行预测。其公式可表示为

式中，yt表示第t时刻的输出值，w0为权重矩阵，b0为偏差向量。激活函数为Sigmoid激活函数。最后输出预测目标车辆t时刻的加速度值。st为上一层的输出矩阵。

1.3 理论-数据驱动组合模型

为了融合理论驱动、数据驱动两种模型的优点，结合理论模型的理论可靠性优势和数据驱动模型在拟合数据和模拟驾驶员的记忆效应方面的优越性特点，采用最优加权法［19］建立理论-数据驱动组合模型。设理论模型和数据驱动模型的权重系数分别为α1和α2，有α1+α2=1。et1和et2分别为t时刻理论模型和数据驱动模型的预测误差值，t时刻模型的组合误差为

组合模型的误差平方和为

组合模型的最优权重系数为求esum的最小值问题。组合模型的最终输出公式为

α＇1、α＇2分别为最优权重系数法确定的最优权重值。k1为理论模型得到的预测值，k2为CNN-Bi-LSTM-Attention模型得到的最优预测值。

2 数据准备

2.1 数据说明

本研究采用无人机视频轨迹数据库（http：//seutraffic.com），该数据为江苏省南京市应天大街高架桥一段限速80 km/h的快速路轨迹数据。如图3所示，原始车辆轨迹数据包括车辆编号、横向位置、纵向位置、车道编号、车辆长度、车辆宽度、行驶速度、加减速度等参数，时间精度为0.04 s，位置精度为0.01 m。采集视频覆盖交通流从自由流运行到拥堵的整个演变过程。数据中包含1 041辆车辆数据，共822 712条数据。原始数据说明如表1所示。

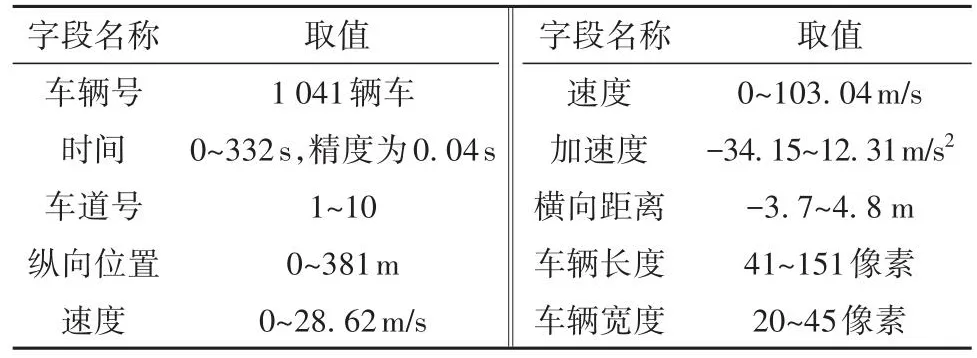
表1 数据说明Table 1 Data description

图3 车道示意图Fig.3 Lane diagram

2.2 构建数据样本集

2.2.1 提取前向车辆

根据车辆在相同时间内在同一车道上的车辆纵向位置关系，标定车辆在不同时刻的前车的车辆号、横向位置、纵向位置、加速度以及速度5个交通参数。

对于得到的数据组，筛选目标车辆在研究车道内行驶时间大于30 s的本车道数据，跟驰前车在研究车道内行驶时间大于15 s的跟驰车辆的数据，筛选得到338辆稳定跟驰行为的车辆组。

2.2.2 提取侧向换道车辆

1）根据如下公式判断车辆是否换道：

式中，lt为车辆在t时刻所处的车道编号，当车辆在t时刻与t+1时刻所处车道号不同时，即为车辆发生换道的时刻。

2）以内侧车道6车道为研究对象，对于从侧方车道换道到6车道的车辆进行统计，得到车辆集合A；对于上一步处理得到的数据，提取前车车辆为从侧方车道换道到6车道的车辆，得到车辆集合B，B为研究的目标车辆，A为相对的侧向换道车辆；车辆B集合中，跟驰前车发生变化的时刻即为换道时刻。选取换道时刻t前后15 s的数据。车辆的跟驰行为在30 s内，不仅受前车的影响，还受换入车辆的影响。根据时间和标定的车辆号两个因素，标定侧方车辆的车辆号、横向位置、纵向位置、加速度以及速度5个交通参数。部分标定数据如表2所示。

表2 部分车辆位置关系数据Table 2 Partial vehicle position relation data

2.3 数据预处理

对于得到的数据组中存在的随机干扰、异常值和测量误差，需要对数据进行降噪处理，数据平滑法是最常用的方法。本研究采用移动平均法对车辆横、纵坐标、速度和加速度进行数据平滑，可表示为

式中，Ft为下一期的预测值，At-1至At-n分别表示前一期至前n期的实际值。

为方便模型训练，采用min-max对模型输入数据分别进行归一化处理后再作为模型的输入，计算公式为

其中，xj为每一项原始数据，xn是归一化处理后的数据，xmean、xmax、xmin分别为数据的平均值、最大值和最小值。

3 模型验证

3.1 模型评价指标

本研究采用归一化数据的平均绝对误差（EMA）、均方误差（EMS）、均方根误差（ERMS）、期望方差（SEV）、拟合优度R2作为目标判别函数。如式（28）-（32）所示：

其中，yi和̂分别表示测试集的真实值和模型预测值，表示真实值的平均值，i表示数据量。EMA、EMS、ERMS的值越小，预测效果越好，SEV和R2取值范围为［0，1］，值越大，预测效果越好。

3.2 理论模型参数标定

在第1节确定的FS-MAVD跟驰模型结构的基础上，根据第2节所得到的车辆数据，以目标车辆分别与前方、侧方车辆两车的纵向间距，目标车辆分别与前方、侧方车辆两车的速度差，目标车辆速度5项指标作为跟驰模型标定的性能指标，选取均方根误差值作为参数标定结果评价指标，用于衡量标定的模型与实际值的差异。采用差分进化算法进行模型的参数标定。

对于模型标定，参考王雪松等［20］确定的参数范围，由于本研究时间间隔为0.04 s，所以在其基础上将参数范围进行调整，得到常量敏感系数a范围为［0.002，0.800］，b、c范围为［0，1］，且b+c=1；安全距离hc为［0.8，8］；相对速度敏感系数λ1、λ2范围为［0.012，0.800］，参数标定结果为a=0.03，b=0.6，c=0.4，λ1=0.13，λ2=0.37，hc=4.2。

3.3 数据驱动模型参数调整

首先是构建CNN-Bi-LSTM-Attention数据驱动模型，通过参数调整，使其预测达到最优效果。对历史长度、训练批次和训练轮数的不同值的结果进行预测，选择最优参数。其次，根据最优参数设置LSTM和Bi-LSTM的参数，得到不同模型的预测结果。

3.3.1 记忆效应影响时长分析

根据孙倩等［17］的结论，对驾驶员的记忆效应进行分析，对1.0～3.0 s内的历史不同影响长度进行分析，如图4所示，得出本模型记忆效应影响时长为2 s，即驾驶员的驾驶行为除了受当前环境影响，还受前2 s的记忆影响。时长为2 s时，判定系数（R2）达到最高97.74%。

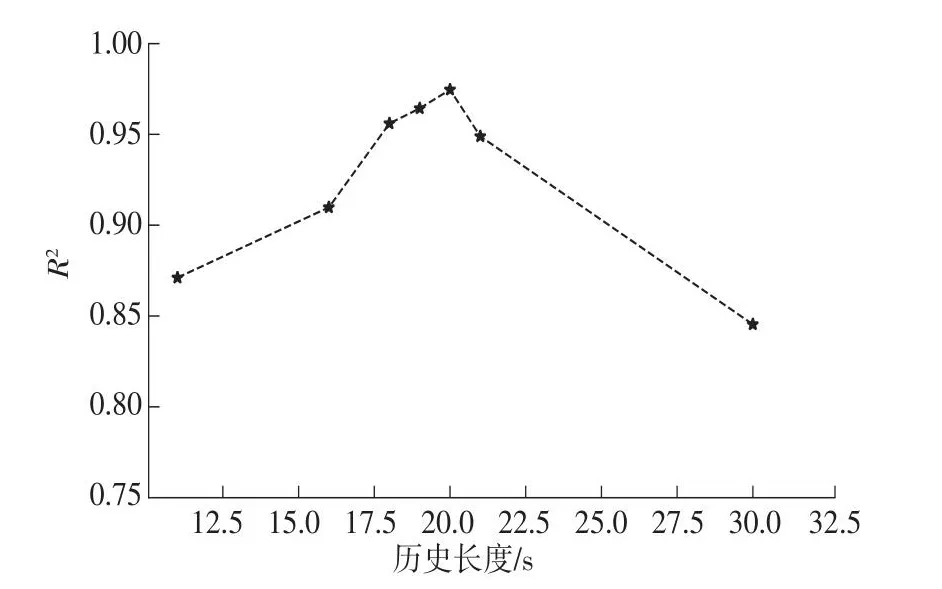
图4 不同历史长度下的判定系数图Fig.4 Determination coefficient diagram of different historical lengths

3.3.2 训练批次和训练轮数

训练批次分别选取32、64和128，如图5所示。发现当其为64时，判定系数（R2）达到最高97.74%。而训练轮数收敛快速，所以训练轮数选择10轮即可。

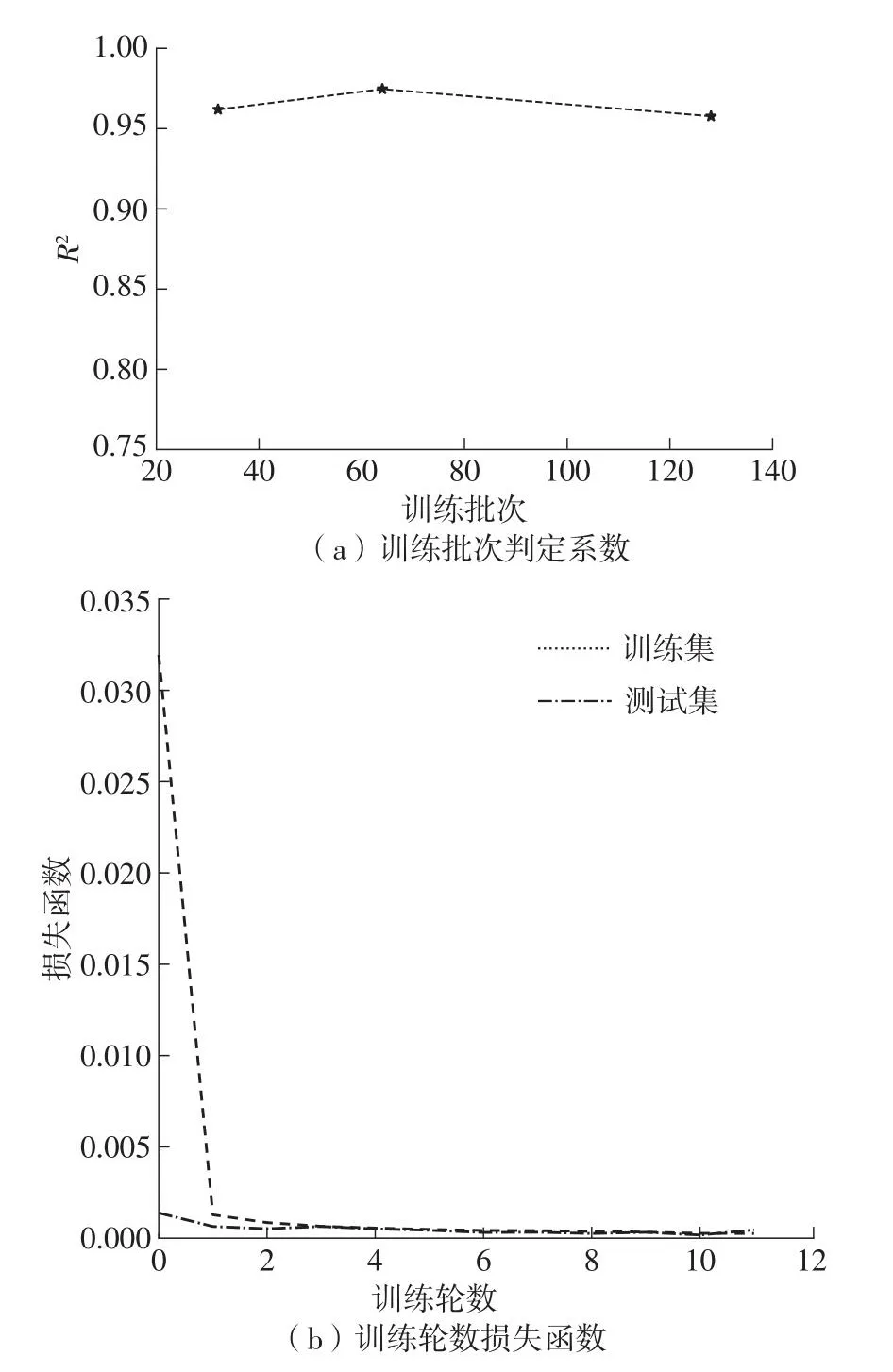
图5 参数调整图Fig.5 Parameters adjustment diagram

3.4 跟驰模型训练结果比较

3.4.1 预测精度对比

将构建的新样本集按训练集与测试集8∶2的比例进行划分后，分别采用LSTM模型、Bi-LSTM模型和CNN-Bi-LSTM-Attention、理论模型和理论-数据组合模型5个模型预测目标车辆的加速度。将测试集上的真实值与预测值进行实际绘图对比验证。测试集中组合模型拟合优度最高达到97.64%，其次为CNN-Bi-LSTM-Attention模型，拟合优度为94.24%。图6示出了测试集中4辆车辆的预测结果，可以直观地看出，在3种数据驱动模型中CNN-Bi-LSTM-Attention模型预测效果更优。理论模型拟合精度较差，但能较好地拟合趋势走向，组合模型拟合效果最好。

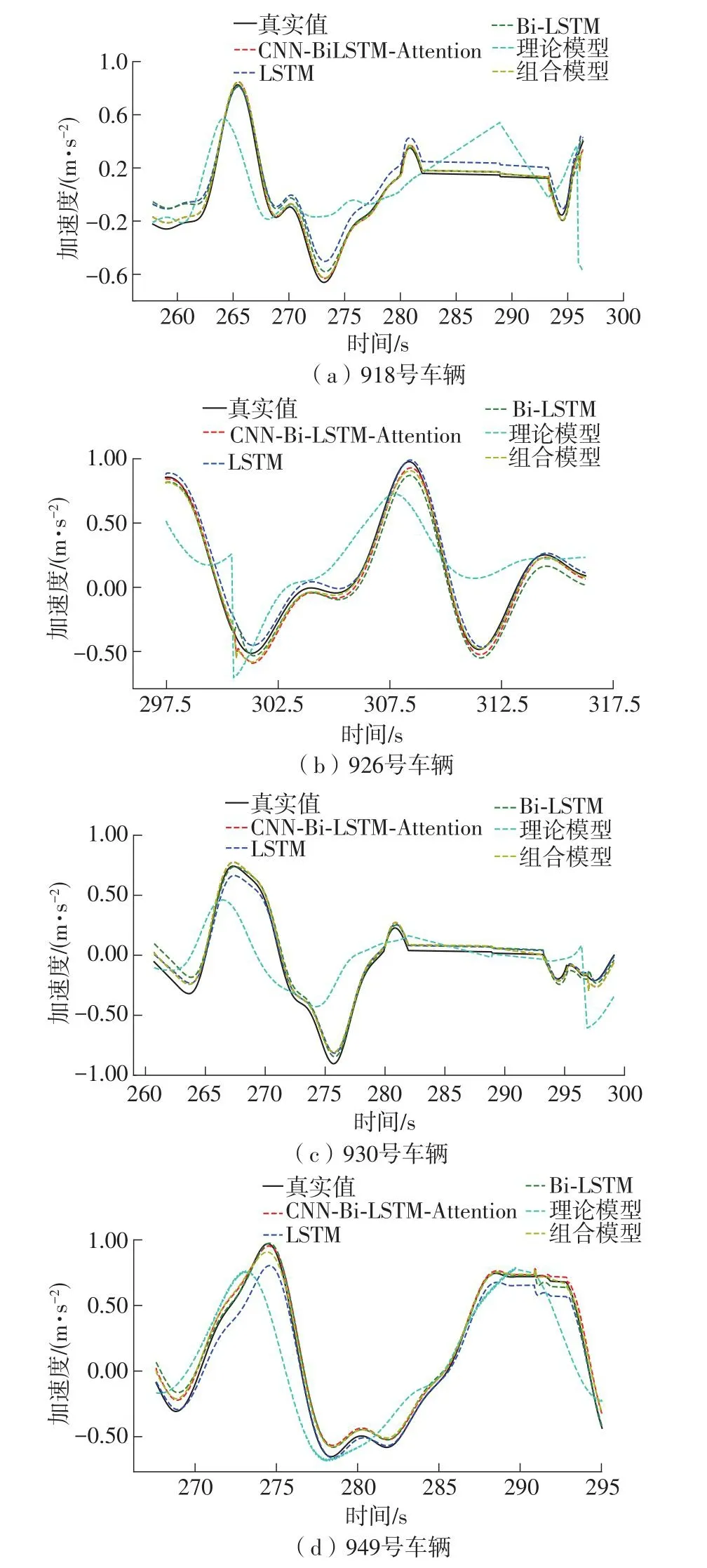
图6 车辆加速度预测结果Fig.6 Predicted results by single vehicle acceleration

在数据驱动跟驰模型方面，CNN-Bi-LSTMAttention模型对不同样本的预测效果不尽相同，但总体而言，预测精度优于另外两种数据驱动模型。CNN-Bi-LSTM-Attention模型对4辆车的拟合精度分别为99.09%、98.94%、98.36%和98.51%，比LSTM模型预测精度提高了7.42%、0.43%、0.13%、0.81%，比Bi-LSTM模型预测精度提高了3.77%、1.64%、1.40%、0.06%。

理论模型除了考虑前方车辆和侧方车辆的间距影响，还考虑到速度影响，可以较好地拟合出趋势走向，但拟合精度较差，且不如数据驱动模型平滑，是因为数据驱动模型考虑了LSTM模型的记忆效应。将理论与CNN-Bi-LSTM-Attention模型预测结果以最优加权法的方法结合起来。从图6和表3可以看出，组合模型预测效果最优，误差最小。组合模型的拟合精度分别为99.1%、99.24%、98.56%、98.74%。

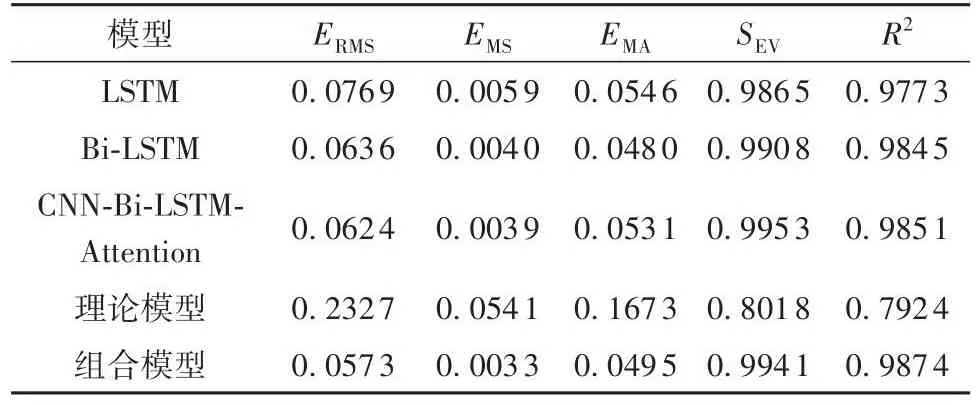
表3 949号车辆预测结果评价Table 3 Evaluation of forecast results of vehicle 949

3.4.2 预测误差对比

图7示出了4辆车辆不同模型下的均方根误差图，CNN-Bi-LSTM-Attention模型均方根误差分别为0.033 3、0.043 4、0.052 1、0.062 4，低于LSTM和Bi-LSTM的预测误差。组合模型预测误差分别为0.026 72、0.036 80、0.050 00、0.057 30。

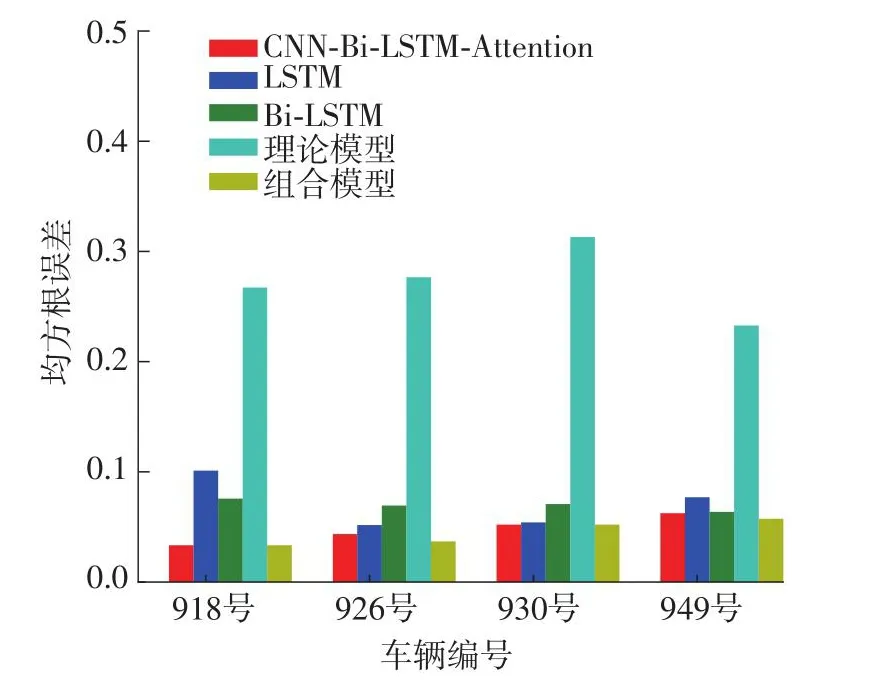
图7 不同车辆不同模型下的均方根误差Fig.7 Root mean square errors of different vehicle models

3.4.3 单一车辆各个模型判别系数的对比

对949号车辆不同模型下的不同判别系数进行统计，结果见表3。可见，总体而言，CNN-Bi-LSTM-Attention模型预测误差（EMA、EMS、ERMS）均低于LSTM和Bi-LSTM的预测误差，拟合优度（SEV、R2）高于LSTM和Bi-LSTM模型。组合模型相对其他模型预测误差更小，预测精度更高。组合模型均方根误差相比LSTM、Bi-LSTM、CNN-Bi-LSTM-Attention、理论模型4种模型误差分别降低1.96%、0.63%、0.51%、17.54%，拟合优度分别提高1.01%、0.29%、0.23%和19.5%。

4 结论

（1）在交通场景方面，考虑了受侧方换道车辆影响的跟驰现象，并依据视频轨迹数据，对于换道现象制定了直线行驶和换道规则，标定了目标车辆的前方车辆和侧方车辆的车辆号及其交通参数，构建了新的样本集。

（2）在模型构建方面，考虑实际车辆行驶过程换道行为对跟驰车辆驾驶安全的影响，分别建立FS-MAVD理论模型和CNN-Bi-LSTM-Attention模型数据驱动模型，采用差分进化算法对理论模型进行参数标定；考虑目标车辆与前方、侧方车辆两车的纵向间距，目标车辆与前方、侧方车辆两车的速度差，目标车辆速度和历史长度T加速度6个主要因素，预测目标车辆T+1时刻加速度；之后采用最优加权法将两种模型进行组合，以结合理论模型的理论可靠性和数据驱动模型拟合精度高的优势。

（3）在模型验证方面，构建的组合模型与LSTM、Bi-LSTM、CNN-Bi-LSTM-Attention、理论模型进行结果对比，通过对比模型之间平均绝对误差、均方误差、均方根误差、期望方差和拟合优度5个判别因素，可以发现，本研究构建的组合模型预测误差相对其他模型误差更低，精确度更高，更接近车辆实际驾驶行为。再通过对具体车辆单独分析，可以发现组合模型均方根误差相比其他4种模型分别降低1.96%、0.63%、0.51%、17.54%，拟合优度分别提高1.01%、0.29%、0.23%和19.5%。通过参数调整发现，当侧方车辆发生换道情况时，驾驶员记忆影响时长约为2 s，数据驱动模型可以平滑交通流的扰动，使预测效果更平滑精确。组合模型结合数据驱动模型的优势与理论模型适用性强的特点，在驾驶行为预测方面有更好的表现。本研究可为车辆在侧方车辆换道情况下对前方和侧方车辆微观驾驶行为的感知判断提供良好的参考，有助于合理规划驾驶行为，对于保证交通安全具有重要意义。