基于高阶统计量偏斜度和赤池信息准则的突涌水微振信号初至拾取方法*

胡慧江 李利平 靳 昊 陈彦好 王 升 黄瑞哲

(1.南京水利科学研究院, 南京 210029; 2.华设设计集团股份有限公司, 南京 210001; 3.山东大学齐鲁交通学院, 济南 250002; 4.白俄罗斯国立技术大学土木工程学院, 明斯克 220013)

随着“一带一路”“交通强国”等国家重大战略的实施,我国公路、铁路、水利水电、市政等基础设施建设迎来黄金发展时期。[1]隧道工程作为公铁领域基础设施建设中的控制性工程,尤其是我国西南部的岩溶地区,在其建设过程中常常遭遇具有大水压、高流量、强隐蔽性特点的突涌水灾害,往往造成巨大的经济损失和人员伤亡。[2-6]微振监测技术作为一种无损监测技术,已经被广泛应用与隧道岩爆、矿山冲击地压、边坡失稳、石油开采、地热能开发等领域。微振监测技术通过监测岩体内部的破裂,实现对孕灾区位置的安全、无损监测。在突涌水灾害演化过程中,隔水岩体受水压、爆破等动力扰动伴随产生微振事件,为监测突涌水演化过程提供重要物理表征。[7-8]从微振监测技术原理考虑,利用微振监测技术获取掌子面前方突水通道定位信息的重要前提是计算准确的微振信号到时,以提供更为精准的计算事件定位的基础数据。

传统的微振信号拾取方法主要包含了人工拾取和自动拾取。人工拾取虽然在一定程度上有着较高的精度,但是对操作人员的拾取经验要求较高,效率低,时耗大,难以应对大量的微振数据处理;且长时间的人工拾取易使操作人员产生厌烦情绪,影响拾取精度甚至漏拾的情况。为了提高微振数据处理效率,实现全天候的灾害监测,20世纪70年代开始开始逐渐涌现出一批利用微振信号与噪声信号差异特征的自动拾取技术,如长短时窗均值比方法(STA/LTA)[9-10]、高阶统计量偏斜度(PAI-S)[11]、赤池信息准则(AIC)[11-12]、小波变换[13-14]等方法。赤池信息准则是将AIC理论引入到自回归模型中来获取微振信号的初至时刻。但是该方法抗干扰能力差,对未经降噪处理的微振信号拾取精度较低。高阶统计量偏斜度方法主要是利用数学方法对微振信号进行处理,其原理是寻找一段有限长度的微振信号偏斜度函数曲线斜率最大的位置即为微振信号的初至时刻。尽管PAI-S对含有噪声的微振信号具有较强的抗干扰能力,但是该方法较为依赖滑动时窗的大小,从而影响微振信号到时时刻的拾取效率。

针对上述问题,开展了突涌水微振事件信号到时自动拾取算法的研究,并以室内突涌水灾害微振监测模型试验微振信号为例,对方法适用性和先进性进行对比分析,为事件空间定位计算提供参考。

1 PAI-S和AIC到时拾取方法

1.1 PAI-S到时拾取方法原理

高阶统计量偏斜度(PAI-S)方法[11]是Saragiotis于2002年提出的一种基于数学统计方法的微振信号自动拾取方法。其偏斜度计算式为:

(1)

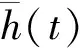
该方法原理主要是基于偏斜度函数,其主要计算步骤为:

1)输入一段长度为M的源信号h(t)=1,2,3,…,M;2)在源信号中设置一个长度为N的滑动时窗,并假设滑动时窗N的中心点为m;则滑动时窗N可以将源信号h(t)划分为M-N+1个具有数据重叠的信号段;3)计算每个M-N+1个信号段内的偏斜度值,并将其赋予中心点m;4)将每个信号段的偏斜度依次衔接得到源信号h(t)的偏斜度曲线;5)计算所得到的源信号h(t)的偏斜度函数曲线斜率最大值,即为该信号的初至时刻。

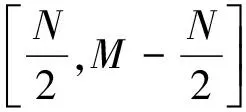
1.2 AIC到时拾取方法原理

AIC微振信号初至时刻拾取是基于自回归模型的统计学方法,其中最为常用的方法是Maeda提出的VRC-AIC方法。该方法基于微振信号初至时刻前后的统计特性差异来确定微振信号的初至时刻。其原理大致为:对于一段长度为L的微振信号,在其序列内设置一滑动点k(k=1,2,3,…,L),可以将信号划分为[1,k]和[k+1,L]两个信号序列,当VRC-AIC值最小时,即为初至时刻。整个信号序列的VRC-AIC算式可表示为:

αVRC-AIC(k)=klg[σ2(S[1,k])]+(L-1-k)

lg[σ2(S[m+1,m])]

(2)

式中:σ2(S[1,k])、σ2(S[m+1,m]) 分别为滑动点k划分的两个信号序列的方差。

VRC-AIC方法属于二阶统计量方法,保证其初至时刻拾取精度须满足两个假设:

1)最小的相位单元须是AIC;2)给定的原始信号中尽量只包含高斯白噪声。

在实际应用中,尤其是复杂隧道施工环境中,包含了大量噪声信号(车辆行驶、喷浆、风枪施工等),难以满足上述两个假设,因此该方法较PAI-S方法对噪声的抵抗能力更弱,拾取精度难以保障。

2 S-AIC到时拾取方法

针对上述两种方法存在的问题,提出一种基于PAI-S和AIC的微振信号初至时刻拾取方法,该方法的步骤如下:

1)通过偏斜度计算出一给定长度信号的偏斜度曲线,并求出整条曲线斜率最大的时刻。

2)提取偏斜度曲线斜率最大时刻对应的滑动时窗中所有的偏斜度值Sk。

3)将输出的偏斜度值Sk作为特征值,代入式(2),替换由VRC-AIC方法中由动点划分出的两个信号序列的方差,进行S-AIC运算,其计算式为:

βS-AIC(k)=klg[σ2(Sk[1,k])]+(L-1-k)·

lg[σ2(Sk[k+1,L])]

(3)

4)当βS-AIC(k)取最小值时,输出k值,即k对应的时刻即为初至时刻。

βS-AIC(k)初至拾取方法的拾取流程如图1所示。

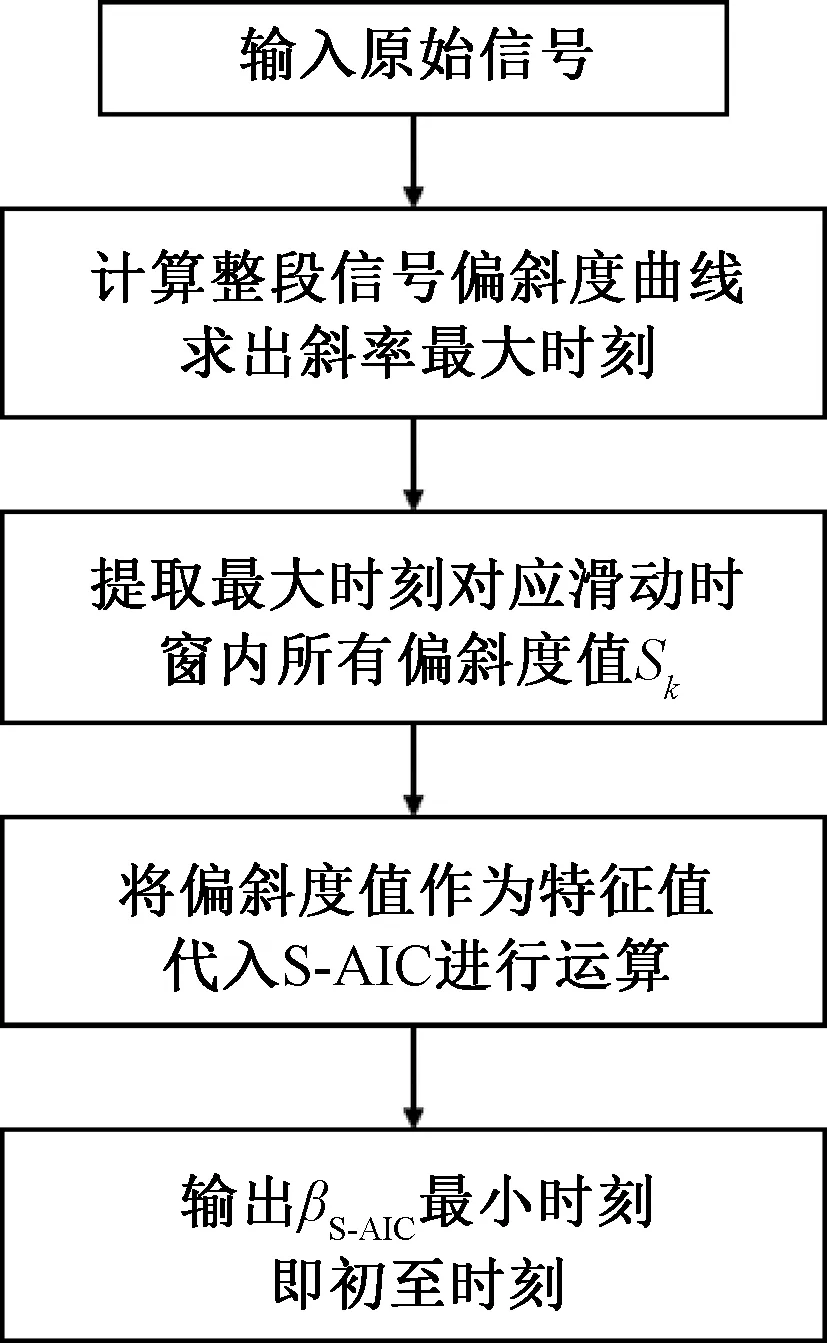
图1 S-AIC初至拾取方法流程Fig.1 The flow chart of the S-AIC first break picking method

3 突涌水微振监测试验数据分析

选取已开展的高地应力隧道突涌水模型试验[15]的试验数据进行验证,如图2所示,试验选用监测仪器的监测频率为8 kHz。试验设定的水平地应力和竖向地应力均为1.5 MPa,水压力大小为2.5 MPa。试验体规格尺寸为1 000 mm×1 000 mm×1 000 mm,所需材料计算用量的质量比为,水泥∶砂∶水=284∶1 448∶278。

a—高地应力隧道突涌水试验场景; b—试验系统原理。图2 高地应力隧道突涌水模型试验Fig.2 A model test of water inrush in tunnels under high crustal stress

地应力场全部加载完成后,首先向试验体内注入1 MPa的低水压进行初始地下水渗流环境模拟;60 min后正式开始试验,水压设置为2.5 MPa,待初始地应力和水压稳定后,采用东成Z1C-FF03-26型手持式钻机模拟隧道连续开挖掘进过程,直至岩体发生完全破坏且发生突涌水。采用8支单分量速度型传感器进行微振事件采集。由现场分析可知信号源除微振事件源之外,存在水压泵、液压机和环境干扰等噪声源。

选取一组高信噪比信号和一组低信噪比信号进行验证。高信噪和低信噪比原始信号分别如图3、图4所示。

图3 高信噪比突涌水微振信号Fig.3 Microvibration signals from water inrush with high signal-to-noise ratios

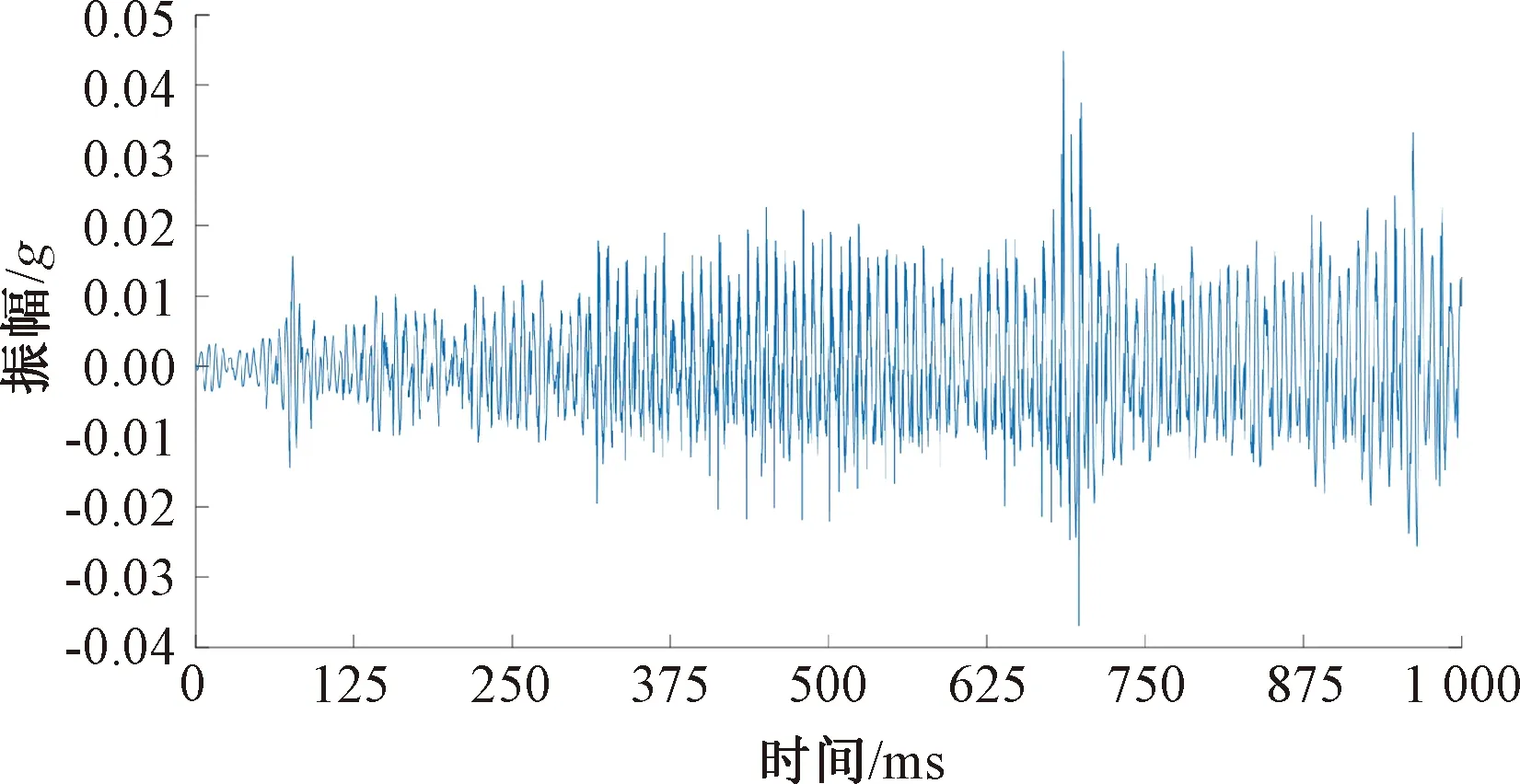
图4 低信噪比突涌水微振信号Fig.4 Microvibration signals from water inrush with low signal-to-noise ratios

针对上述两类信号,选取滑动时窗N为160、170、180、190、200分析S-AIC、AIC、PAI-S及人工拾取方法初至时刻拾取精度,图5、图6所示为滑动时窗N为160时高、低信噪比突涌水微振信号初至时刻拾取结果(其余滑动时窗大小拾取结果不再单独列出)。不同滑动时窗下三种方法及人工拾取方法初至时刻拾取结果如图7、图8及表1和表2所示。其中人工拾取时间采用波形放大后观察首波起跳位置而划定的初至时间(图9),存在一定经验性误差,文中按常规操作拾取值。

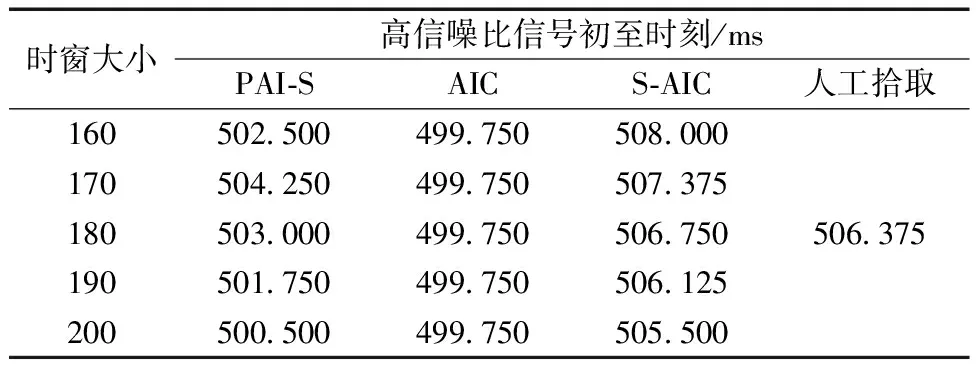
表1 不同方法高信噪比信号初至时刻Table 1 Initial arrival-moments of high signal-to-noise ratio signals by different methods

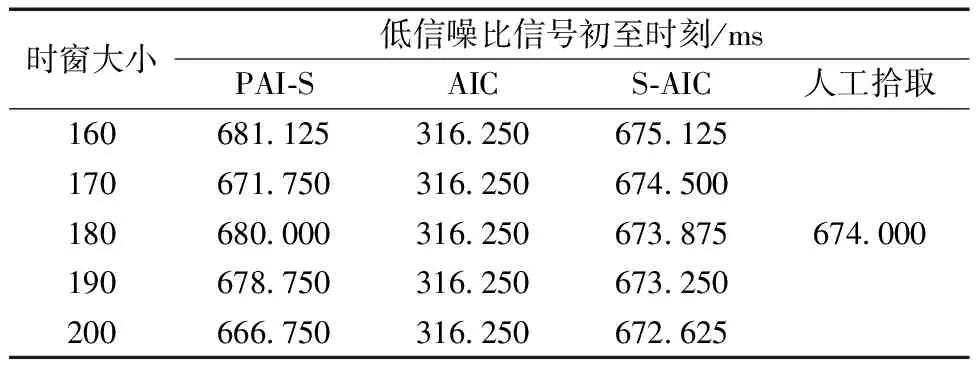
表2 不同方法低信噪比信号初至时刻Table 2 Initial arrival-moments of low signal-to-noise ratio signals by different methods

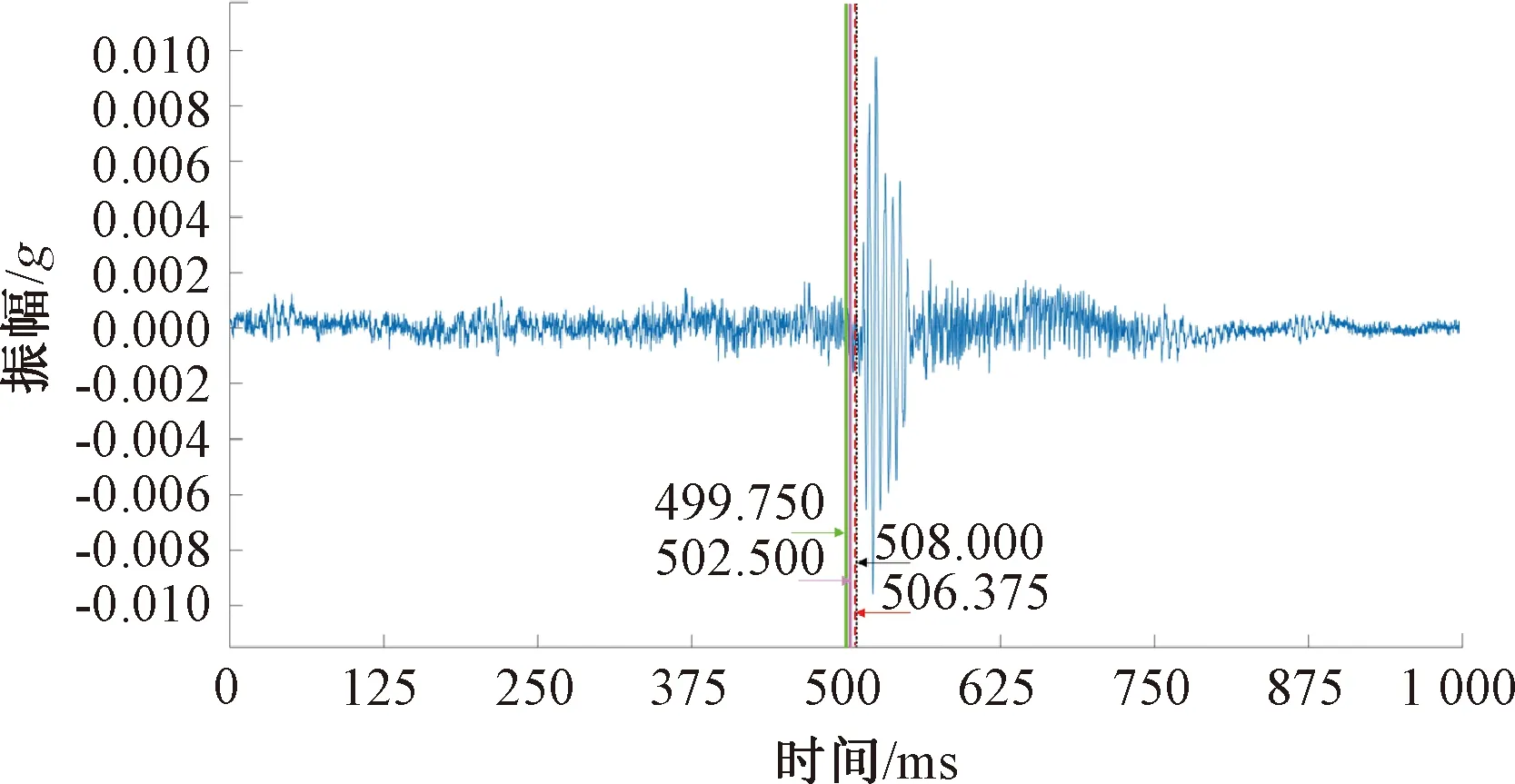
信号; S-AIC; AIC; PAI-S; 人工拾取。图5 时窗160时高信噪比信号初至时刻拾取结果Fig.5 Pickup results for initial arrival-moments of high signal-to-noise ratio signals with a time window of 160

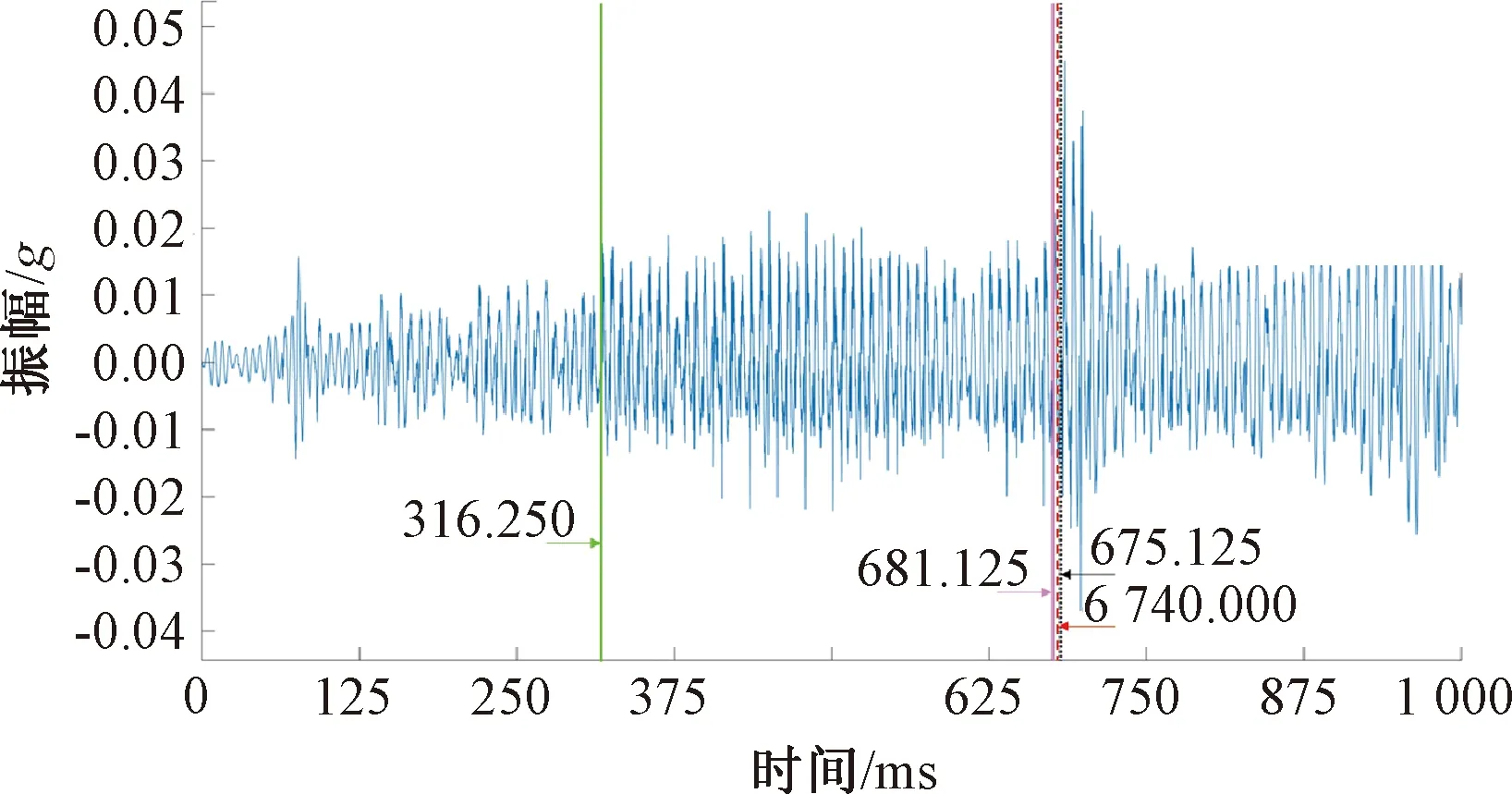
信号; S-AIC; AIC; PAI-S; 人工拾取。图6 时窗160时低信噪比信号初至时刻拾取结果Fig.6 Pickup results for initial arrival-moments of low signal-to-noise ratio signals with a time window of 160

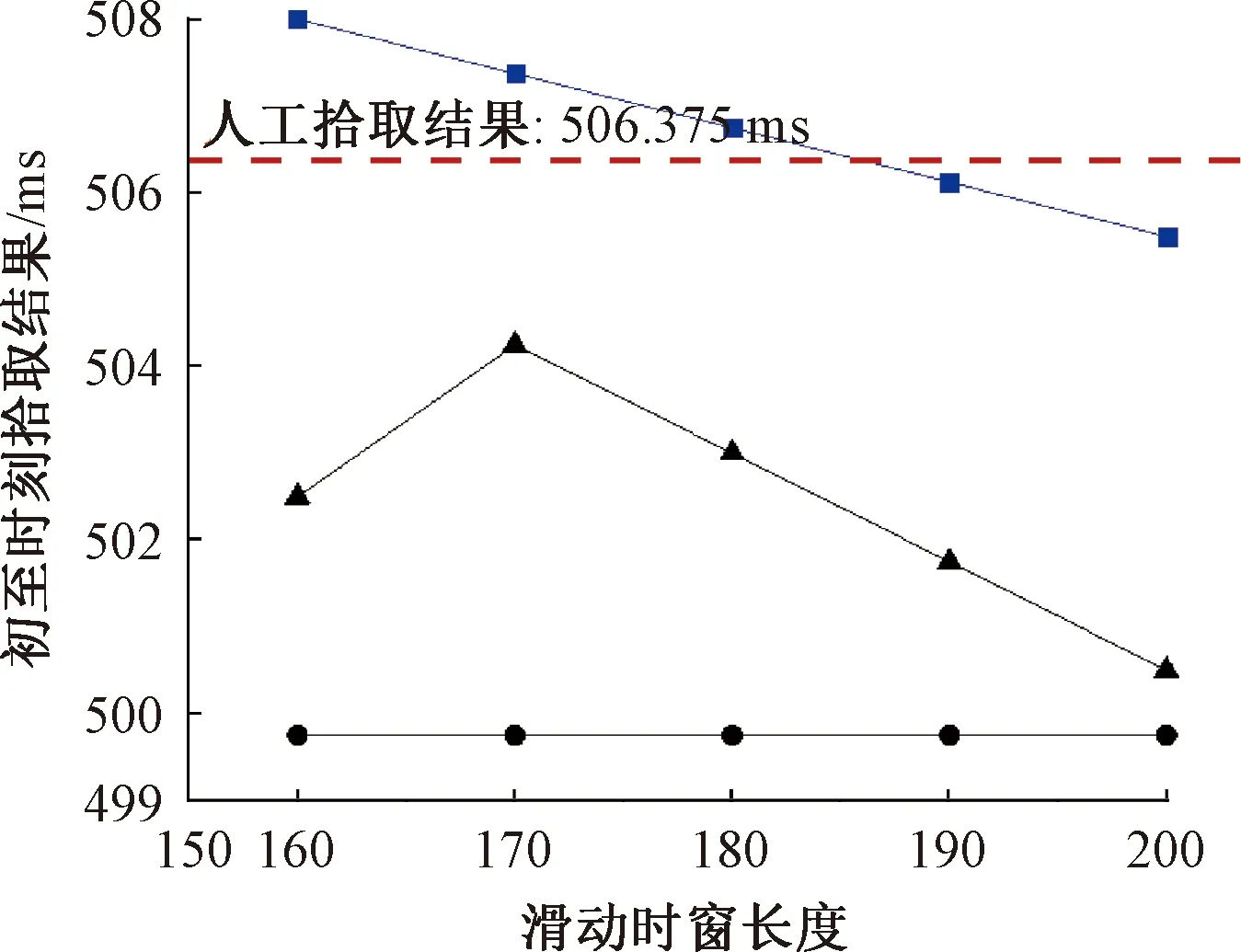
S-AIC; —AIC; —PAI-S。图7 不同时窗时高信噪比信号初至时刻拾取结果Fig.7 Pickup results for initial arrival-moments of high signal-to-noise ratio signals with different sliding window sizes

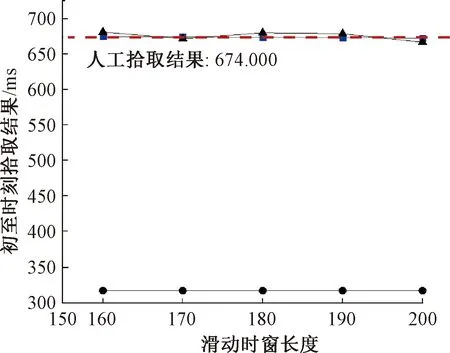
S-AIC; —AIC; —PAI-S。图8 不同时窗时低信噪比信号初至时刻拾取结果Fig.8 Pickup results for initial arrival-moments of low signal-to-noise ratio signals with different sliding window sizes

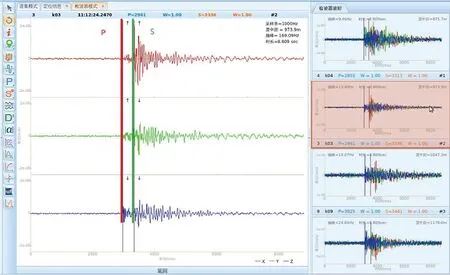
图9 常规商业软件人工手动边界拾取Fig.9 Manual boundary extraction from a conventional commercial software

可以看出:AIC方法对高信噪比突涌水微振信号能够拾取到一个较为准确的初至时刻。但当信号为低信噪比突涌水微振信号时,其拾取精度受自身的局限性,无法拾取到较为准确的初至时刻。

同时,从表1可以看出:对高信噪比信号而言,S-AIC和PAI-S方法在相邻滑动时窗大小下初至时刻的差值基本稳定在一个固定值(S-AIC方法差值为0.625 ms,PAI-S方法差值为1.250 ms),且S-AIC方法更接近人工拾取的结果。由表2可见:对低信噪比信号而言,PAI-S方法在相邻滑动时窗大小下差值具有较大离散性,而S-AIC方法仍具有较高的稳定性(S-AIC方法差值仍为0.625 ms),且初至时刻拾取更加接近人工拾取方法的结果。

为进一步分析PAI-S与S-AIC方法对两种突涌水微振信号的初至时刻拾取效果,以人工拾取的初至时刻为基准,对比不同时窗下PAI-S与S-AIC两种方法的准确性,结果如表3和表4所示。

表3 高信噪比信号PAI-S与S-AIC拾取精度分析Table 3 Analysis on pickup accuracy of PAI-S and S-AIC signals with high signal-to-noise ratios

表4 低信噪比信号PAI-S与S-AIC拾取精度分析Table 4 Analysis on pickup accuracy of PAI-S and S-AIC signals with low signal-to-noise ratios

由表3可知:当信号为高信噪比信号时,S-AIC和PAI-S两种方法在以人工拾取为基准的初至时刻的绝对误差区间分别为0.250～1.625、2.125～5.875 ms。两种方法的平均绝对误差分别为0.825,3.975 ms,以平均绝对误差为评价指标时,S-AIC方法较PAI-S方法初至时刻拾取精度提高了3.125 ms。由表4知:当信号为低信噪比信号时,S-AIC和PAI-S两种方法在以人工拾取为基准的初至时刻的绝对误差区间分别为0.125～1.375、2.250～7.250 ms。两种方法的平均绝对误差分别为0.775,5.475 ms,以平均绝对误差为评价指标时,S-AIC方法较PAI-S方法初至时刻拾取精度提高了4.700 ms。通过上述对比,验证了S-AIC方法较PAI-S和AIC方法具有一定的优越性,滑动时窗大小及信噪比对其拾取精度影响较小。

4 结束语

提出了一种基于PAI-S和AIC的突涌水微振信号到时拾取方法,分析了PAI-S和AIC两种方法的局限性;利用已开展的模型试验获取的突涌水微振信号验证了该S-AIC初至时刻拾取方法优越性。研究得到了以下结论:

1)AIC方法适用于高信噪比突涌水微振信号,对于低信噪比信号初至时刻拾取精度较差。

2)PAI-S方法同时适用高信噪比和低信噪比突涌水微振信号的初至时刻拾取,但是滑动时窗大小对其拾取精度影响较大。

3)利用PAI-S和S-AIC两种方法对已开展的模型试验获取的突涌水微振信号初至时刻进行拾取,对于高信噪比和低信噪比信号,S-AIC方法较PAI-S方法初至时刻拾取精度分别提高了3.125,4.700 ms

4)提出的S-AIC方法对高信噪比信号和低信噪比信号的初至时刻拾取精度更佳,滑动时窗的大小对该方法影响较小。