基于空间受力性能最优化的箱梁带斜梁空间刚架模型*

2023-07-26宋泰宇郑信光孙旭霞白志娟

工业建筑 2023年5期

宋泰宇郑信光孙旭霞白志娟

(1.同济大学建筑设计研究院(集团)有限公司, 上海 200092; 2.同济大学土木工程学院, 上海 200092)

0 引言

混凝土箱梁桥广泛应用于国内外桥梁建设中,在混凝土箱梁结构的设计和分析中,目前一般采用有限元模型进行数值计算,常用的有限元模型(表1)主要包括:1)6自由度梁单元模型,工程中一般称为“单梁模型”,单梁模型在截面的竖向、横向均不离散化,因此模型无法考虑箱梁的空间效应,工程设计中一般通过横向分布系数、剪力滞系数等放大系数将由箱梁空间效应带来的受力不均匀性“包络住”[1];2)实体(或板壳)模型,实体模型中结构在纵、竖、横三个正交方向上均离散化,因此可以完全不受平截面假定的限制,自动反映结构所有空间效应,模型计算结果中同时包含整体效应和局部效应,但由于实体模型的计算结果难以直接交付到构件设计层面,因此目前工程中多用于复杂结构的局部受力分析;3)以单梁模型和实体模型作为上、下界,介于二者之间的其他类型有限元模型的复杂程度和计算精度也相应地介于单梁和实体模型之间。例如:梁格模型沿截面横向有离散化,因此可以考虑箱梁各腹板受力不均匀和剪力滞效应,但由于梁格模型沿截面竖向没有离散化,即箱梁顶、底板没有分离,因此不能准确考虑箱梁的薄壁效应,梁格模型本质上可以视为横向分片的单梁模型[2]。

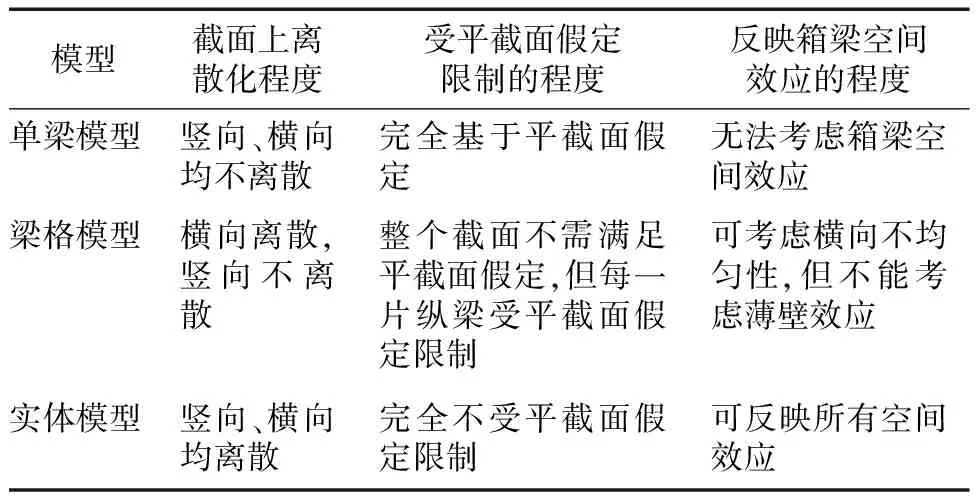
表1 箱梁结构数值分析常用有限元模型对比Table 1 Comparison between different FEA models commonly used for analyzing box-section girders

混凝土箱梁(不论单箱或多箱)结构上一般由腹板、顶板、底板组成,如图1所示,箱梁板厚方向的尺寸一般远小于其在纵桥向、横桥向的尺寸,因此属于典型的板壳结构,要准确且高效地模拟混凝土箱梁,最为直接、有效的途径是将箱梁离散为平板单元,进而采用板壳模型进行有限元模拟和分析[3];而另一方面,为了与现行的混凝土箱梁配筋设计规范相联系,工程设计用模型一般仍限于基于杆系单元(杆单元或梁单元)的有限元模型。

图1 典型的混凝土箱梁结构Fig.1 A typical concrete box-section girder

鉴于上述这两方面,不同学者提出了由平板等效而来的杆系单元模型,典型的有两种:平面桁架模型[4-10]和空间刚架模型[11-14],如图2所示。平面桁架模型(图2a)是将平板单元用铰接的3自由度杆单元进行等效,模型中的杆单元只能承受轴力(二力杆),节点无面外自由度,因此平面桁架模型适用于平面结构分析,部分学者还将平面桁架模型进一步拓展到非线性分析领域[8-10];空间刚架模型(图2b)是将平板单元用刚接的正交6自由度梁单元进行等效,由于空间刚架模型对箱梁结构进行了三维离散化,且模型中正交梁单元的节点具有承受面外弯矩的自由度,因此空间刚架模型可以反映结构空间效应。

a—平面桁架模型; b—空间刚架模型。图2 两种由平板等效而来的杆系模型示意Fig.2 Two beam or truss element models used to simulate plate

文章旨在建立一个以平板为结构基本组成单元的等效数值分析模型,可以准确且高效地对混凝土箱梁进行精细化数值分析,具体来说,建立的模型需要能够考虑箱梁的空间效应,准确反映箱梁各板件的面内、面外效应,特别是准确模拟板件的面内剪切性能,这要求建立的模型同时满足两个条件:1)在箱梁横截面的竖向和横向上均须离散化;2)模型基本组成单位须是杆系单元,以方便解决预应力、车道荷载施加以及内力提取等桥梁模型的典型前后处理问题。

为了同时满足上述要求,结合平面桁架模型和空间刚架模型的优点,提出了一种新型的带斜梁空间刚架模型,如图3所示,提出的新模型在空间刚架模型的基础上增设了沿斜向布置的梁单元,该带斜梁空间刚架模型中,正交纵横梁和斜向梁均为6自由度梁单元,节点可承受面外弯矩,因此该模型可用于三维结构的空间分析;同时,斜梁参与结构的整体剪、扭受力,直接提供(补充)了平板的面内剪切刚度,斜梁的分析结果可直接反映出受剪板件在主应力方向的受力性能,进而可以准确、高效地判断和分析混凝土箱梁各板面上由主拉应力引发的斜裂缝。

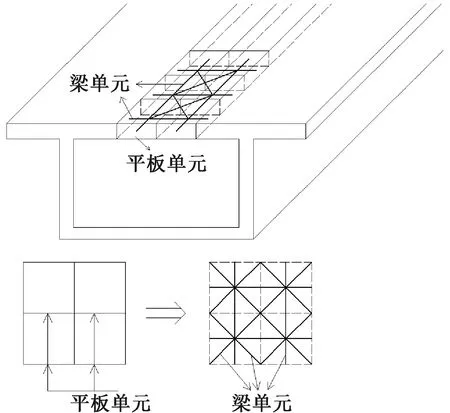
图3 提出的带斜梁空间刚架模型示意Fig.3 Proposed spatial grid model with diagonal beam elements

1 带斜梁空间刚架模型的建立

1.1 模型建立转化为最优化问题

与平面桁架模型和空间刚架模型类似的,提出的带斜梁空间刚架模型中各杆件的参数也须通过和平板单元建立刚度等效关系来确定。对于平面桁架模型,其各杆件的唯一参数,即轴向刚度可通过面内刚度等效原则[4-5]或能量法[6-7]确定;对于空间刚架模型,其中正交的梁单元截面为平板单元的截面[11-12],因而模型的面内轴向刚度和面外抗弯刚度与平板自动等效,分析可得其面内剪切刚度与平板剪切刚度的比值恰为1+μ(μ为结构材料的泊松比)。但是与上述两个已有等效模型不同的是,对于带斜梁空间刚架模型来说,由于斜梁和正交纵横梁之间相互影响,节点力(或力矩)在交叉节点处按刚度分配,使得带斜梁空间刚架模型中各杆件的受力状态较为复杂,难以采用应变能守恒等理论方法推导得到各杆件参数的显示表达式,因此只能通过规划方法给出该模型中杆件参数的最优值。

如图1和图3所示,箱梁结构可以分解为若干平板,即平板单元可视为箱梁的基本组成单位。箱梁结构在各类桥梁静力外荷载作用下,平板单元的受力状态可以视为面内轴压、面内纯剪、面外纯弯这三种基本荷载作用形式的不同组合,因此文中箱梁等效模型的建立可以转化为平板单元在这三种基本荷载作用下的刚度等效问题。

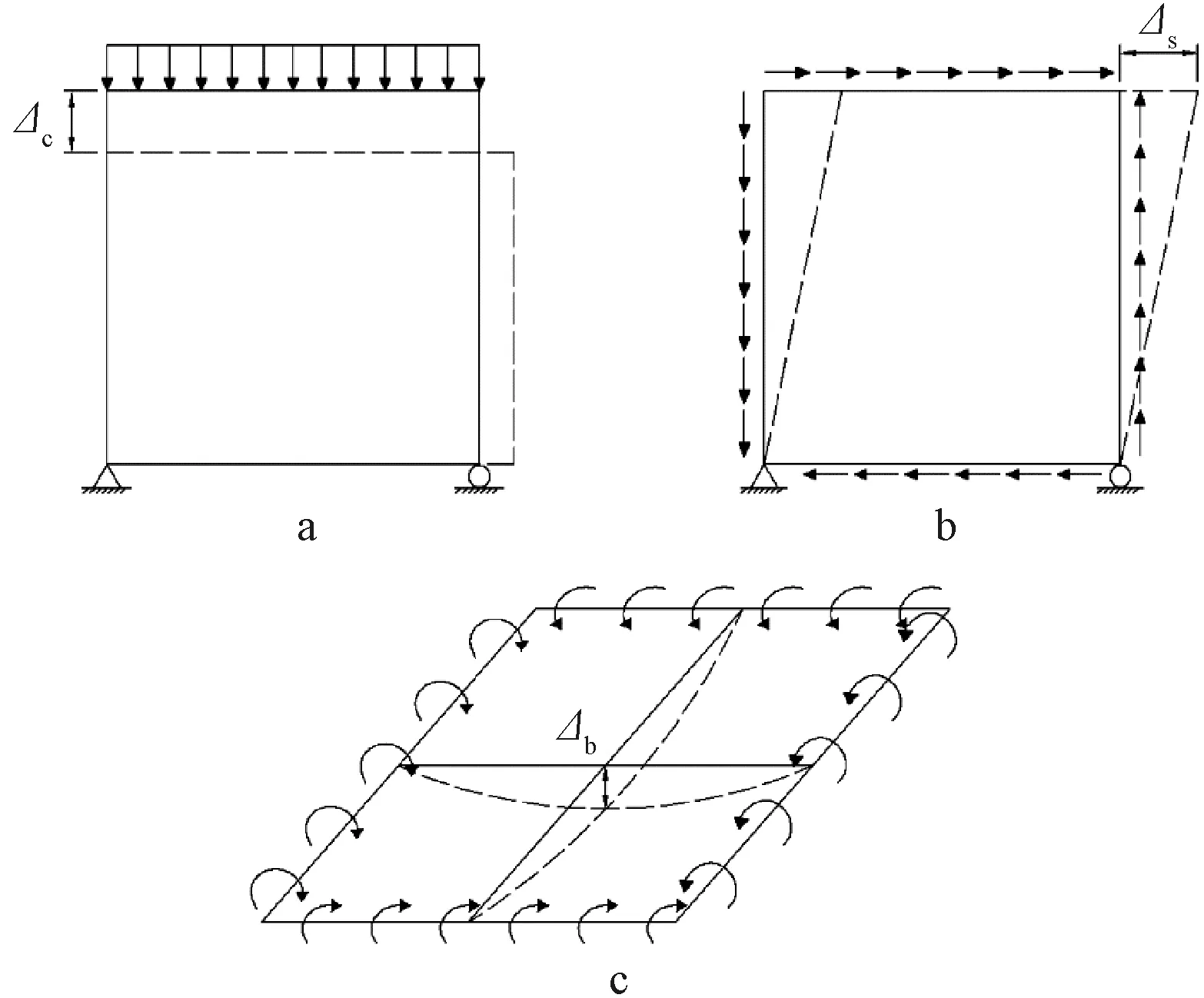
a—面内轴压作用; b—面内纯剪作用; c—面外纯弯作用。图4 三种基本荷载作用下的正方形平板单元Fig.4 Square plate elements under three basic types of loads

(1c)

式中:目标函数xc、xs、xb分别为轴压、纯剪、纯弯下带斜梁空间刚架模型与平板变形量的相对误差。由式(1)可以看出,该最优化问题含有3个目标函数和2个参数变量(hvh、hdia),即为多参数、多目标值最优化问题。若3个目标函数的绝对值均可取到零时,说明对应的参数为该问题的最优解;若3个目标函数绝对值不能均取到零时,说明该问题不存在最优解,只存在条件最优解[15]。当只存在条件最优解时,可设置一个大于零的容许误差值(Error),使目标函数xc、xs和xb的绝对值均小于该Error值,显然,设置的Error值越接近零,对应的条件最优解也就越优秀。

1.2 多目标值、多参数最优化问题求解

为了求解上述多目标值、多参数最优化问题,以图4所示的正方形平板为例,平板边长l=1.0 m,板厚t=0.025 m,平板的材料弹性模量E=3.45×107kN/m2,泊松比μ=0.2。平板分别受面内均布轴压作用(每一边上轴压合力N=2.5×103kN)、面内均布纯剪作用(每一边上剪力合力V=2.5×103kN)和面外均布纯弯作用(每一边上弯矩合力M=2.0 kN·m)。根据上述给定参数值,可计算得平板在这三种基本荷载作用下的理论变形值Δc、Δs和Δb分别为[16-17]:

(2a)

(2b)

(2c)

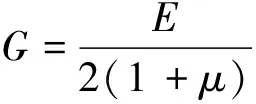
A=lt

式中:G为平板的剪切刚度;A为均布轴压和剪切荷载作用面面积;D为(薄)板的抗弯刚度[17-18]。

图5 模型参数最优化求解流程Fig.5 Flowchart of optimization of parameters in the model

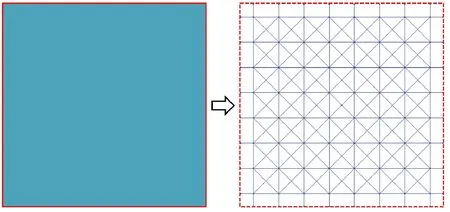
图6 平板转化为8×8带斜梁空间刚架模型示意Fig.6 Translation from a plate to the 8×8 spatial grid model with diagonal beam elements

图7为在三种基本荷载作用(面内轴压、面内纯剪、面外纯弯)下,带斜梁空间刚架模型程序计算的变形值与对应理论值的相对误差(即式(1)中目标函数xc、xs、xb)随模型参数(hvh、hdia)的变化曲面,另外,各图中还给出了目标函数xc、xs、xb的绝对值小于0.1的对应参数位置,用黑色×标志示出。由图中可以看出,在三种基本荷载作用下,随着参数(hvh、hdia)的减小,带斜梁空间刚架模型的结构刚度逐渐下降,对应的变形值逐渐增大,因此模型计算值和理论值的相对误差由小于零逐渐过渡为大于零,形成了三个穿越了参考面(x=0)的变化曲面,这表明在三种基本荷载下,均存在目标函数绝对值小于0.1的参数,也说明两个参数设定的可行域是合理的。另外,对比各图还可以看出,在斜向梁的梁高(hdia)逐渐减小过程中,纯剪作用下模型计算变形值的增大速度明显大于另外两种基本荷载形式,说明斜梁在带斜梁空间刚架模型中对抗剪刚度的贡献明显大于其对抗压、抗弯刚度的贡献,这与力学判断的结果也是相符的。

a—面内均布轴压作用(图4a); b—面内均布纯剪作用(图4b); c—面外均布纯弯作用(图4c)。图7b中只示出了x<10的部分。图7 三种基本荷载作用下目标函数随参数的变化Fig.7 Variations of objective functions with different parameters under three basic types of loads

将图7中三种基本荷载作用对应的3个目标函数xc、xs、xb绝对值均小于0.1的参数点同时叠置于同一平面上,如图8a所示,其中,×标记(黑色)、o标记(红色)和+标记(蓝色)分别对应面内轴压、面内纯剪和面外弯曲作用下的参数点,那么可知,这三类标志的重合点对应的参数值即为式(1)满足容许误差Error=0.1时的条件最优解。由图8a可以看出,三种基本荷载作用下存在重合点且不唯一,说明式(1)存在多个对应Error=0.1的条件最优解。为了找到更为优秀的条件最优解,将容许误差Error以0.5%为一级逐级下调,由图8b可以看出,当Error=0.065时,式(1)存在唯一条件最优解,对应参数值为hvh=102.50 mm、hdia=31.875 mm;由图8c可知,当Error=0.060时,无重合点,说明式(1)已不存在条件最优解。

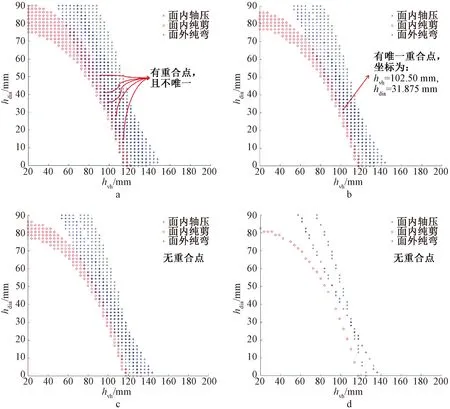
a—Error=0.1; b—Error=0.065; c—Error=0.060; d—Error=0.01。图8 不同允许误差(Error)下三种基本荷载作用对应的条件最优解Fig.8 Conditional optimal solutions corresponding to three basic types of loads under different allowable errors

综上所述,可以确定hvh=102.50 mm、hdia=31.875 mm为文中最优化问题,即式(1)的最佳条件最优解,对应的Error=0.065,说明采用该参数值建立的带斜梁空间刚架模型在三类基本荷载作用下计算变形值与理论值的相对误差均在±6.5%以内。

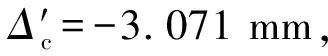
下面给出不失一般性的带斜梁空间刚架模型的建立方法,首先将分析结构拆散为任意多个正方形平板的组合,对于任意边长为l和板厚为t的正方形平板(t/l应不大于1/10),在将平板单元等效转化为n(纵梁)×n(横梁)的带斜梁空间刚架模型时,正交纵横梁和斜向梁的梁宽b均取平板的实际板厚,即b=t;正交纵横梁的梁高hvh取102.50/125=0.82倍的纵横梁实际截面宽度,即hvh=0.82·l/n;斜向梁梁高hdia取31.875/125=0.255倍的纵横梁实际截面宽度,即hdia=0.255·l/n。

2 带斜梁空间刚架模型的示例验证

为了验证上述提出的基于空间受力性能最优化的带斜梁空间刚架模型的准确性和适用性,采用下面两个典型结构进行计算和分析作为示例验证。

2.1 自由端受集中力的悬臂梁

本示例采用图9所示的矩形截面悬臂梁,悬臂梁一端固接、一端自由,自由端受一集中力P作用,梁高为10 mm,梁宽为1 mm。计算两种情况下自由端的挠度:1)梁长L=100 mm,P=10 N;2)L=20 mm,P=103N。悬臂梁的弹性模量E=3.45×107kN/m2,泊松比μ=0.2。

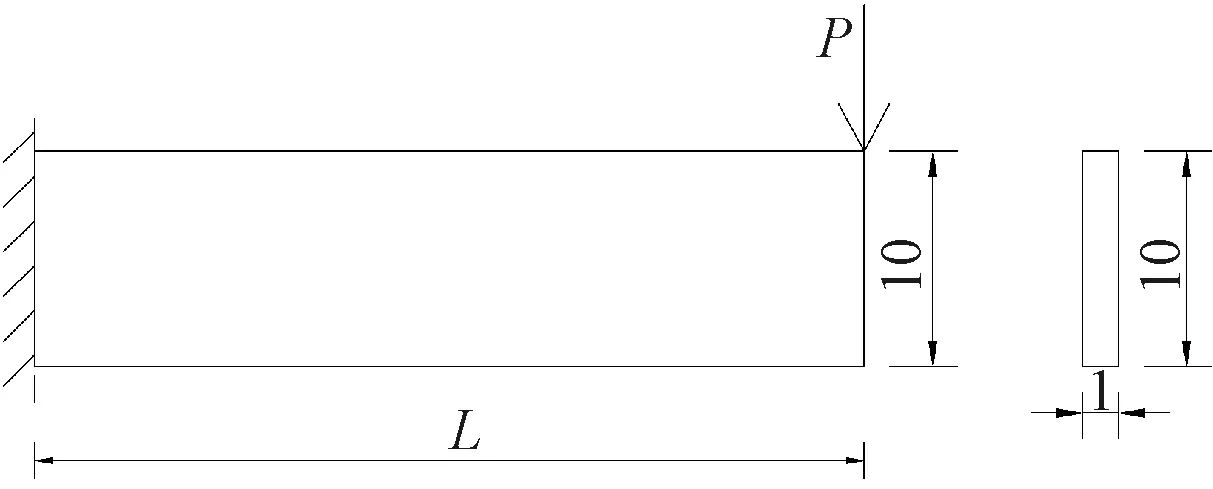
图9 自由端受集中力的悬臂梁 mmFig.9 Cantilever beam subjected to a concentrated load at the free edge

分别采用材料力学(分为不计剪切变形和计入剪切变形)[16]、实体有限元模型以及本文提出的带斜梁空间刚架模型四种方法进行计算。其中,实体有限元模型中,单元特征尺寸取1 mm,带斜梁空间刚架模型中,纵横梁网格尺寸取2.5 mm,则hvh=0.82×2.5=2.05 mm,hdia=0.255×2.5=0.637 5 mm。

带斜梁空间刚架模型计算得的悬臂梁(L=20 mm)变形如图10所示,四种方法计算得的悬臂梁自由端截面形心处竖向挠度如表2所示。以计入剪切变形的材料力学的计算结果(同弹性力学结果)作为标准值,对比可以看出,不计剪切变形的材料力学方法计算结果较标准值偏小,且偏差随梁长的减小而增大,这是因为梁长缩短后剪切变形占总变形的比例增大,梁长L=20 mm时,剪切变形占比达到了15%。实体模型不论梁长的大小,其结果均与标准值非常接近,实体模型不受平截面假定的限制,可以考虑剪切变形的影响。带斜梁空间刚架模型的计算结果较标准值略偏大,主要是由于上述基于三种基本荷载下变形得到的最优化参数解在轴压和纯弯下刚度略偏小,从而导致模拟的悬臂梁在弯曲作用下整体刚度偏小、变形偏大,可以看出,当梁长缩短后,由于剪切变形占比增加,带斜梁空间刚架模型的相对偏差随之减小,L在20 mm到100 mm范围内变化时,带斜梁空间刚架模型的相对偏差应在5%到8%之间,这与上述的条件最优解对应的允许误差6.5%相对应。

图10 悬臂梁(L=20 mm)带斜梁空间刚架模型计算的竖向挠度 mmFig.10 Deflections calculated from the spatial grid model with diagonal beam elements for the cantilever beam (L=20 mm)

表2 悬臂梁自由端截面形心处竖向挠度对比Table 2 Comparison of the deflections at the free edge of cantilever beam mm

2.2 受均布荷载作用的简支箱梁

示例采用图11所示的箱形截面简支梁,简支箱梁在全梁长受均布荷载q,梁高162 mm,箱梁的顶、底板板厚12 mm,腹板厚20 mm。计算两种情况下跨中截面的挠度:1)梁长L=3 000 mm,q=10 N/mm;2)梁长L=1 500 mm,q=100 N/mm。简支箱梁的弹性模量E=3.45×107kN/m2,泊松比μ=0.2。

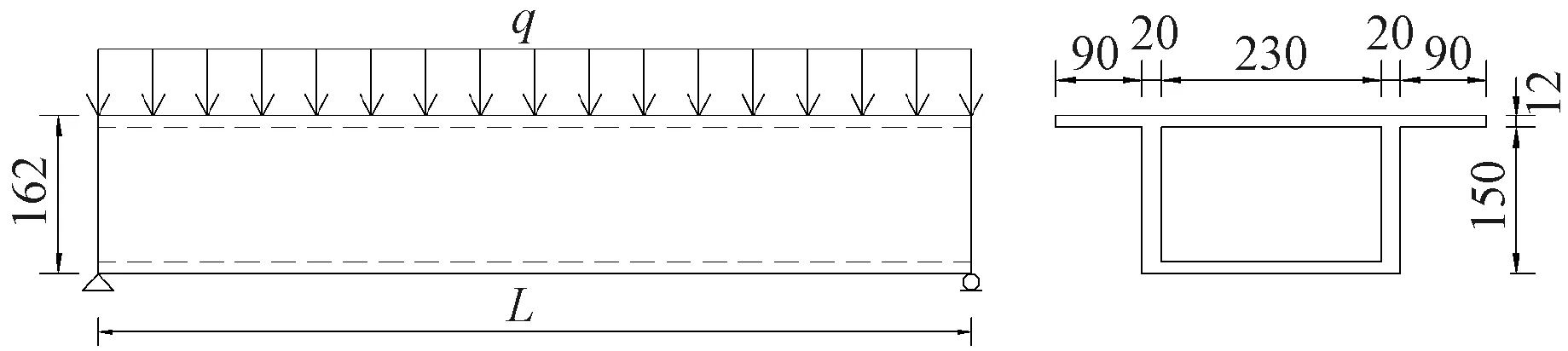
图11 受均布荷载的简支箱梁 mmFig.11 Simply supported box-section girder subjected to uniform loads

同样采用材料力学(分为不计剪切变形和计入剪切变形)[16]、实体有限元模型以及本文提出的带斜梁空间刚架模型四种方法进行计算。其中,实体有限元模型中,单元特征尺寸为10 mm,带斜梁空间刚架模型中,纵横梁网格尺寸选取为50 mm,则hvh=0.82×50=41 mm,hdia=0.255×50=12.75 mm。简支箱梁(L=1 500 mm)对应的带斜梁空间刚架模型如图12所示。

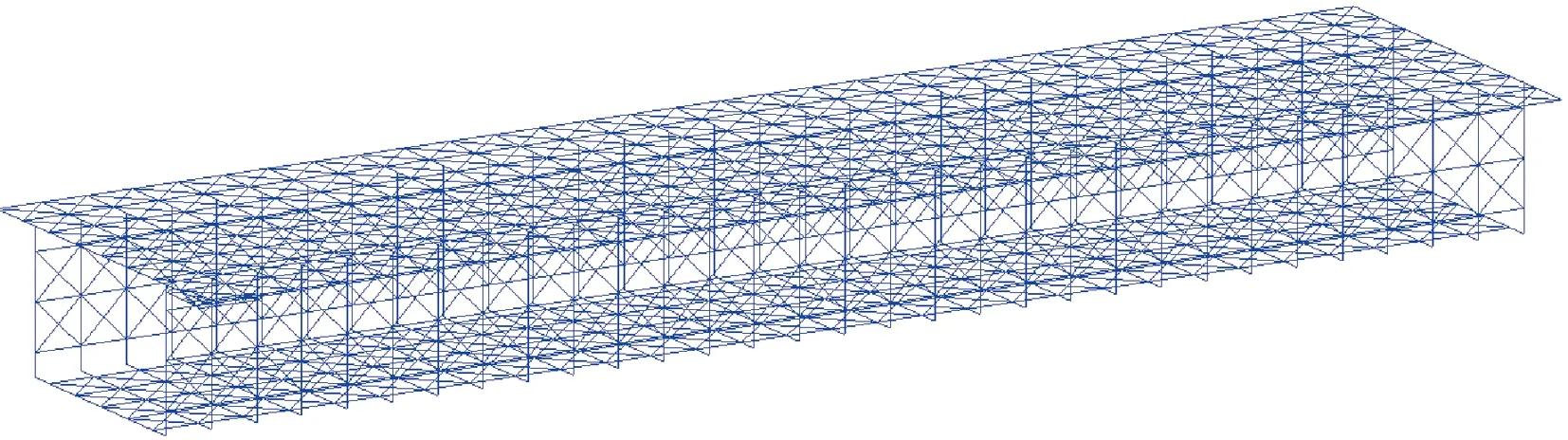
图12 简支箱梁(L=1 500 mm)对应的带斜梁空间刚架模型Fig.12 Spatial grid model with diagonal beam elements for the simply supported box-section girder (L=1 500 mm)

各方法计算得到的简支箱梁跨中截面腹板处竖向挠度如表3所示。同样以计入剪切变形的材料力学计算结果作为标准值,对比可以看出:不计剪切变形的材料力学方法给出的结果与上示例的规律一致,当梁长L缩短到1 500 mm时,剪切变形占比上升到15%。实体有限元模型在L=3 000 mm时,其计算结果与标准值基本一致,而当L缩短到1 500 mm时,实体模型计算的挠度较标准值偏大约12%,其原因主要是:实体模型支座处的约束是梁底边缘上的线约束,因此存在应力集中,支承附近局部存在变形较大的畸形单元,且由于梁长较短,导致该部分局部变形占总变形的比例较大。当将实体模型支承处加入刚性垫板(实体有限元模型*)时,支承附近的应力集中效应显著减弱,该实体模型的计算结果与标准值较为接近。

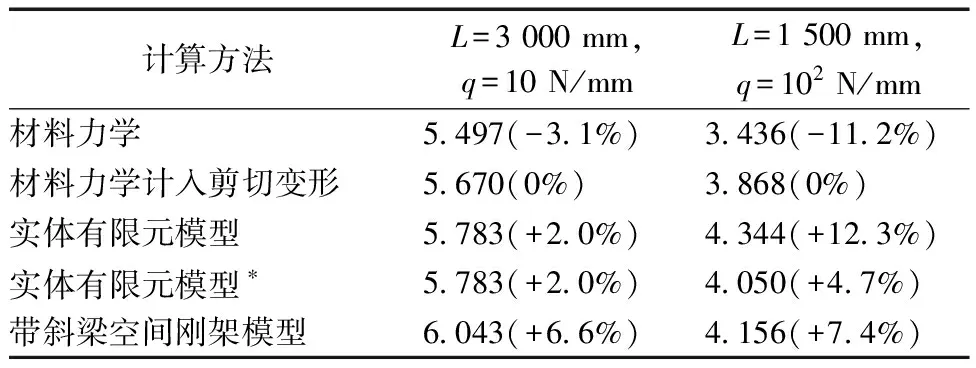
表3 简支箱梁跨中截面腹板处竖向挠度对比Table 3 Comparison of deflections at the midspan section of simply supported box-section girder mm

与上示例相同的,带斜梁空间刚架模型的计算结果较标准值略偏大,相对偏差应在6%到8%之间。另外还需指出的是,受竖向均布荷载作用的简支梁内存在竖向正应力,竖向正应力随梁长缩短而逐渐显著,当梁长缩短到深梁范畴时,竖向正应力可达到与纵向正应力(弯曲应力)同一数量级[17-18]。材料力学方法(计入或不计入剪切变形)无法考虑由竖向正应力引起的变形,而带斜梁空间刚架模型和实体模型可以考虑,因此二者的竖向挠度中实际上还包含了竖向正应力对变形的影响,但鉴于该部分引起的变形量远小于弯曲效应引起的变形量,因此本示例中仍以材料力学(计入剪切变形)方法的计算结果作为标准值。