藏族历史文化村镇聚落斑块特征研究*

胡 昂 普 昊 宋 远 邬文洁

(1.四川大学建筑与环境学院, 成都 610065; 2.东京大学生产技术研究所, 东京 163-8001)

0 引 言

藏族历史文化村镇依据当地的地域环境和民族民俗自发地生长,逐渐衍生出形态万千的村镇聚落形态模式。藏族历史文化村镇建筑形态特征鲜明显著,承载着丰富的地域性特色和先人的智慧,是人类和自然和谐共生的产物。

近年来,伴随着藏族地区社会经济的不断发展,城镇化建设加快了脚步,现代主义设计思想充斥在传统藏族建筑的营建方法中,新文化的强势入侵对藏族文化背景下聚落行为模式和生活方式的改变,导致了传统的聚落格局被打破,营建特征及民族特色逐渐缺失。处于弱势的地域文化如果缺乏内在的活力,将会湮没在世界文化趋同的大潮中[1]。少数民族聚落的传统特征的流失,往往是从最小的聚落单元——建筑斑块单体出发,逐渐发展至更大的区域,最终导致聚落整体风貌遭到不可逆转的改变。因此,研究以现有的14个藏族历史文化村镇为例,借助GIS、数理统计等技术手段,以实地调研和地理信息数据为基础,采用基于分形理论和领域分割理论的量化方法,分别从斑块单体和整体两个层面,研究藏族传统聚落的建筑斑块特征,对于促进未来藏族村镇的新型城镇化建设和乡村振兴战略的良性发展具有积极意义。

1 研究对象

历史文化名村、名镇是中华民族精神文明财富的物化积淀,它们的存在反映了人类历史上各个地域环境特有的一种经济、文化和社会现象[2]。截至目前,国家住建部和文物局共公布了七批次中国历史文化村镇名单,共计799个,并先后评选出了487座历史文化名村和312座历史文化名镇。自2005年四川省莫洛村入选第二批中国历史文化名村后,诸多藏族村镇受到重视,参加了申请评选。本研究即是以目前入选中国历史文化名村、名镇的14个藏族聚落为对象(表1)。

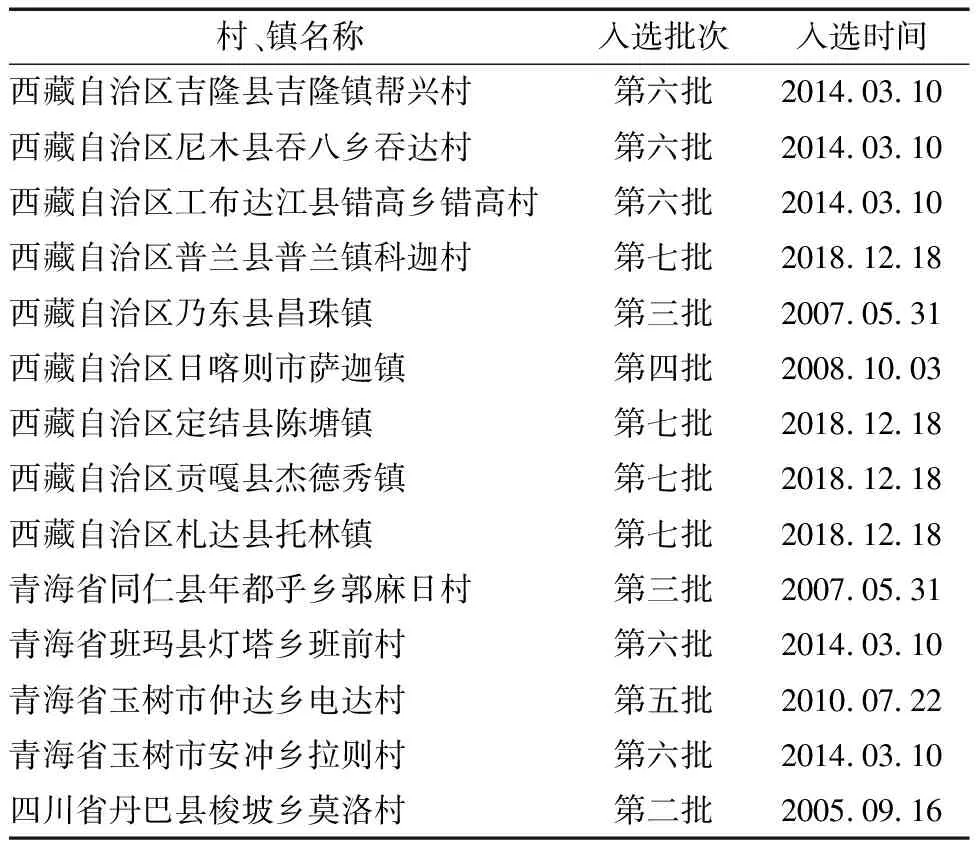
表1 入选中国历史文化名村、名镇的藏族聚落Table 1 Selected Chinese historical and cultural villages, towns of Tibetan settlements

2 研究方法

2.1 分形理论

分形指破碎和不规则,对空间进行研究的过程中需要通过分形维数来描述其形态特征[3]。简单来讲,分形几何就是通过基础的数学逻辑思维和语言抽象表达复杂事物,将复杂概念几何化,揭露复杂事物隐藏的规律,探索事物的本质结构。藏族传统聚落是典型的自组织系统。这样的传统聚落的建筑群体布局,在空间结构形态上具有某种自相似性,而且这种相似性具有分形的特点[4]。因此,运用分形理论及方法研究聚落空间的结构是可行的。

2.1.1建筑斑块分维数

聚落空间在二维层面的核心要素为面积与边界,基于已有城市规划设计及建筑学领域的分形研究方法,以分形学为基础的传统乡村聚落空间图斑绘制及分维值计算方法如下:以30 m为最大长度绘制村落边界,绘制完成后外移2.5 m所得范围作为研究对象,除去住居及围合院落、天井等部分,其余所有空间视作聚落公共空间。将形成的图底关系用公共空间黑色、非公共空间白色表示[4],以此为依据绘制了村落空间图斑,运用“分维值计算公式”计算建筑斑块分维数:

(1)

式中:D为建筑斑块分维数;P为斑块周长;A为斑块面积。可知,D值越大,表明斑块形状越复杂,D值的理论范围为1.0～2.0,1.0代表形状最简单的正方形斑块,2.0表示等面积下周边最复杂的斑块[5]。

2.1.2建筑斑块密度指数

这一概念出自景观生态学,斑块密度指数PD为:

(2)

式中:N为景观中斑块类型的数量;A为景观总面积。PD即为单位面积上的斑块数,它是描述景观破碎化的重要指标,其值越大,破碎化程度越大[6]。

2.2 领域分割

一个聚落本身存在领域性,同时,聚落内部的单体建筑与其他单体建筑间也存在领域性,聚落内与领域外也存在着领域性[7]。但其领域性并不能够通过调查者观察发现,可以从较高的视角出发,通过数理计算分析,捕捉聚落中存在的领域和边界,并通过社会性视域来图式化呈现出来。

2.2.1Voronoi基本理论

Thiessen多边形法是研究空间领域分割的重要方法。该方法由美国气候学家Thiessen借鉴1907年俄国数学家Voronoi提出的沃罗诺伊图(Voronoi Diagram)[8]。它最早被应用于气象学,可以根据离散分布的气象站的降雨量来计算平均降雨量[9]。即将所有相邻气象站连成三角形,作这些三角形各边的垂直平分线,将每个三角形的三条边的垂直平分线的交点(也就是外接圆的圆心)连接起来得到一个多边形,此多边形称之为Thiessen多边形。用这个多边形内所包含的唯一气象站的降雨强度来表示这个多边形区域内的降雨强度。

Voronoi图的生成过程如图1所示。在平面空间中存在N个点,称S为所有点的合集:S={(xi,yi)∣0≤i≤N}。设S中的任意一点P(xp,yp)都有且仅有一个Thiessen多边形,反之亦然。基于点P将空间分割成多个Thiessen多边形,称点P为生成元。除了空间边缘的多边形,每个多边形与相邻多边形边界重叠面不相交。共用边界使得多边形间存在多个结点,每个节点由多条边界相交而成,通过调整边界使得任何一个节点M到与之相连的边界所在的多边形内的点P的距离相等,即所有P点在以M为圆心、d(M点到P点的距离)为半径的圆上,且该圆上不存在S中除P点以外的其他点[10]。

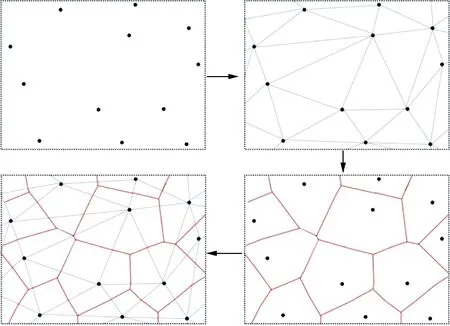
图1 Voronoi图形成过程Fig.1 The formation process of the Voronoi diagram

2.2.2Delaunay三角网理论

Delaunay三角网是1934年由Delaunay根据Voronoi图提出的,GIS中的TIN模型即是利用了这一原理[11]。Delaunay三角网中的所有三角形设定为以空间中的点为顶点,三角形的边不包含顶点,每个三角形与相邻三角形共用一边。

Delaunay三角网的生成如图2所示。对于平面空间中存在的N个点,称V为所有点的合集:S={(xi,yi)∣0≤i≤N}。连接V中的所有外围点形成凸多边形,分别找出离多边形的边最近的点使其与边的端点相连形成三角形,由外向内将V中的点与相邻点相互连接形成若干三角形,并满足没有相交边且边不过点[12]。

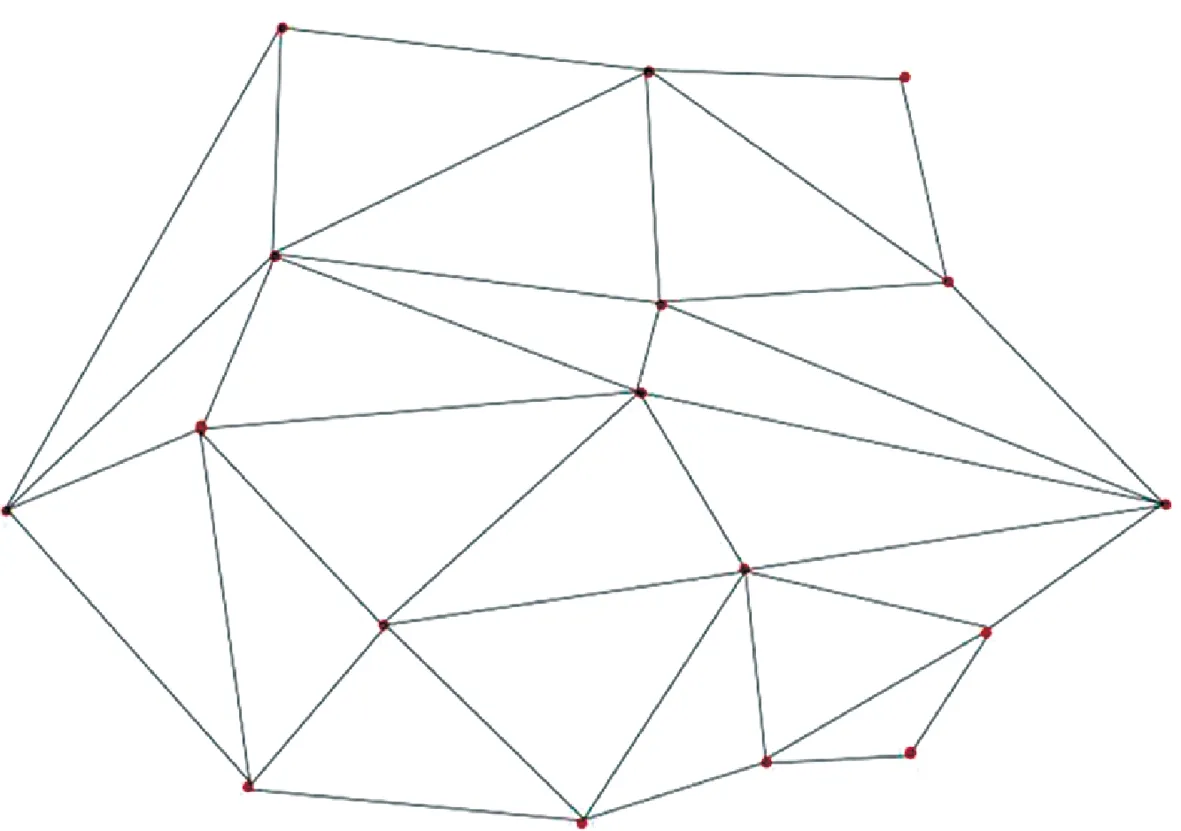
图2 Delaunay三角网Fig.2 Delaunay Triangulation

2.2.3平均最近邻指数

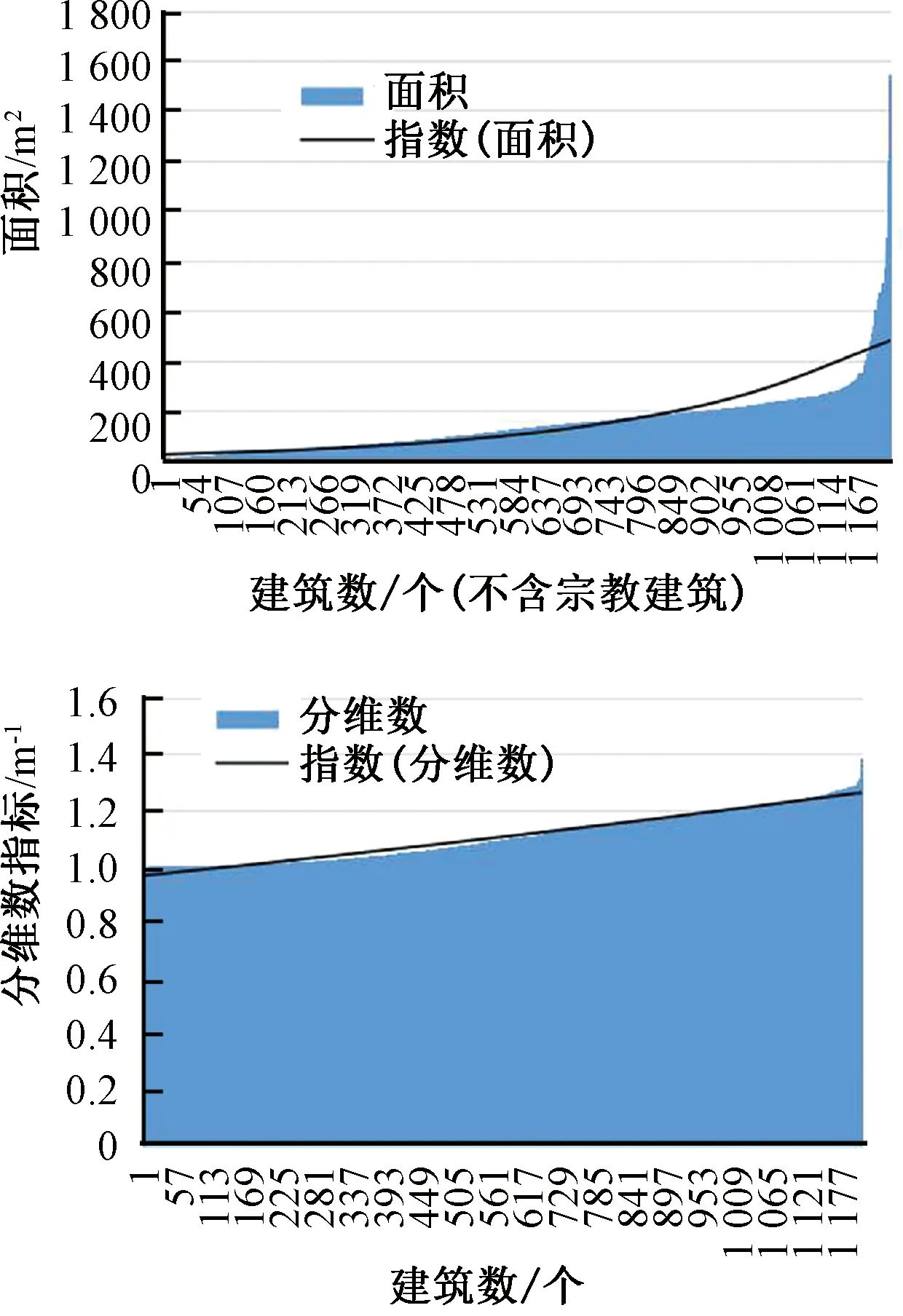
最近邻指数通过每个要素与其最近邻要素之间的平均距离计算。通过点集元素与最邻近点之间距离的平均值和相同数目的点集在理想情况(假定随机分布情况)下的平均距离的比值来判断实际点击分布与期望分布的偏离程度。

最近邻点指数的公式为:

(3)

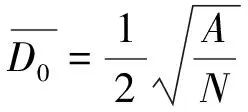
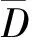
理想情况下,以1作为离散分布与随机分布的界限,但是由于实际情况限制,点集元素空间分布特征的最近邻点指数划分标准会做出相应调整[14],研究以0.8作为划分点集的随机分布和聚集分布的界线。当最近邻点指数R小于0.8时,点集为聚类,即为聚集分布;当R大于0.8时,点集分布表现为趋向离散或竞争。另外还要依据Z分数和P值来判断趋势,数值越小则表明形成过程越随机。

2.3 数据来源

借助Google Earth分别获取14个藏族历史文化村镇的地理坐标数据,通过现场调研勘察和相关文献对其进行细部修正(经过现场调研的村落有错高村、昌珠镇、萨迦镇、杰德秀镇、郭麻日村、班前村、电达村、莫洛村)。然后分别利用CAD、ArcGIS对数据进行可视化表达。最后通过ArcGIS中的统计工具进行数据的整合和运算。

3 聚落斑块单体特征

3.1 分析路径——以杰德秀镇为例

运用基于分维理论的建筑斑块分维数和密度指数来研究聚落斑块单体特征。

以杰德秀镇为例,根据聚落斑块平面图和分维图(图3),利用GIS软件将斑块数据导出后可得斑块面积分布图和斑块分维数指标分布图。杰德秀镇共有建筑斑块约872个,将建筑面积由小到大依次编号,纵轴为建筑面积,横轴为建筑数,得到面积值域分布图(图4a)。

a—聚落斑块配置; b—聚落斑块分维。图3 斑块图示Fig.3 Plaques graphical

a—面积分布; b—分维数指标分布。图4 杰德秀镇建筑斑块面积、分维数分布Fig.4 Distribution map of building plaques area and fractal dimension in Jiedexiu Town

图4b为杰德秀镇建筑分维数指标的分布图,结合平面图3a分析可知,杰德秀镇的建筑多为简单的方形建筑和规整的矩形建筑,但“L”形和“U”形建筑平面也存在一定比例。

3.2 斑块单体形状特征

通过上述步骤对14个藏族聚落依次展开研究,得到所有聚落的数值汇总见表2。可知:郭麻日村、陈塘镇的建筑斑块破碎度较大,帮兴村、错高村、班前村、莫洛村建筑斑块破碎度最小;陈塘镇的建筑斑块紧密度最高,离散度最低;而班前村为离散度最高的聚落。这表明越是紧凑型的聚落,建筑的分布破碎度越高。

括号内数值为分维数在各个值域间的建筑斑块的比例。

单体建筑斑块的分维数,也就是单体建筑的形状与聚落内建筑单体的离散度没有明显的关联,建筑斑块规模越大,院落面积越大的聚落,建筑单体平面形状越丰富,而规模较小的聚落则建筑单体平面越趋近于正方形,且形式非常单一。

4 聚落斑块的配置特征

4.1 研究路径——以郭麻日村为例

以青海省同仁县年都乎乡郭麻日村为例(图5)进行泰森多边形邻域图的绘制。首先,通过Google Earth卫星图(图5a)以及现场调研测绘,提取每个建筑的轮廓,绘制得出建筑平面图。其次,通过ArcGIS软件进行计算,获得每个建筑平面的质点(图5b)。最后,利用浦欣成边界界定理论界定研究的空间边界,对提取出的质心进行Thiessen多边形邻域分析(图5c),计算得到泰森多边形邻域图。

a—卫星图; b—建筑斑块配置; c—泰森多边形邻域。图5 郭麻日村Thiessen多边形邻域分析Fig.5 Neighborhood analysis of Thiessen Polygon in Guomari Village

同样以郭麻日村为例,绘制Delaunay三角网(图6)。首先,将绘制的建筑平面图在ArcGIS上进行大地坐标投影,以获得更准确的地理距离,便于后期建成准确的Delaunay三角网。其次,通过ArcGIS软件进行计算,获得每个建筑平面的质点。最后,基于建筑质点通过ArcGIS进行三角网剖分,得到Delaunay三角网图。

图6 郭麻日村Delaunay三角网Fig.6 Delaunay triangle network in Guomari Village

Voronoi图能较好地表现点集要素的最近邻状态,Delaunay三角网能直观反映空间位置关系,两者存在对偶关系。将Voronoi图中相邻多边形的发生元连接起来即可形成多个不重叠的三角形,共同组成三角形网,即Delaunay三角网。Thiessen多边形的发生元即是Delaunay三角形的顶点,而Thiessen多边形的边即是Delaunay三角形的相邻顶点连线的中垂线(图7)。

图7 郭麻日村对偶关系Fig.7 The duality of the Guomari Village

通过上述分析后,从GIS图示中导出郭麻日村平均最近邻指数值,如表3所示,郭麻日村Z分数为-45.23,P值为0.00,则只有1%或更小的可能性会使该聚类模式是随机过程产生的结果。0.293的最近邻比率表示建筑的分布形态呈现为聚集分布。建筑间的平均最近邻距离值为3.283 m,建筑预期平均距离为11.21 m。参照最近邻指数数据,表明郭麻日村居住单体建筑为聚集分布。

表3 郭麻日村平均最近邻指数Table 3 Average nearest neighbor index of Guomari Village

图8 郭麻日村斑块最近邻指数Fig.8 Sizes of impregnated fiber bundle specimens of Guomari Village

4.2 聚落斑块分布形态

通过上述方法依次计算,并汇总出14个藏族历史文化村镇的最近邻比率和聚落斑块分布形态,见表4。

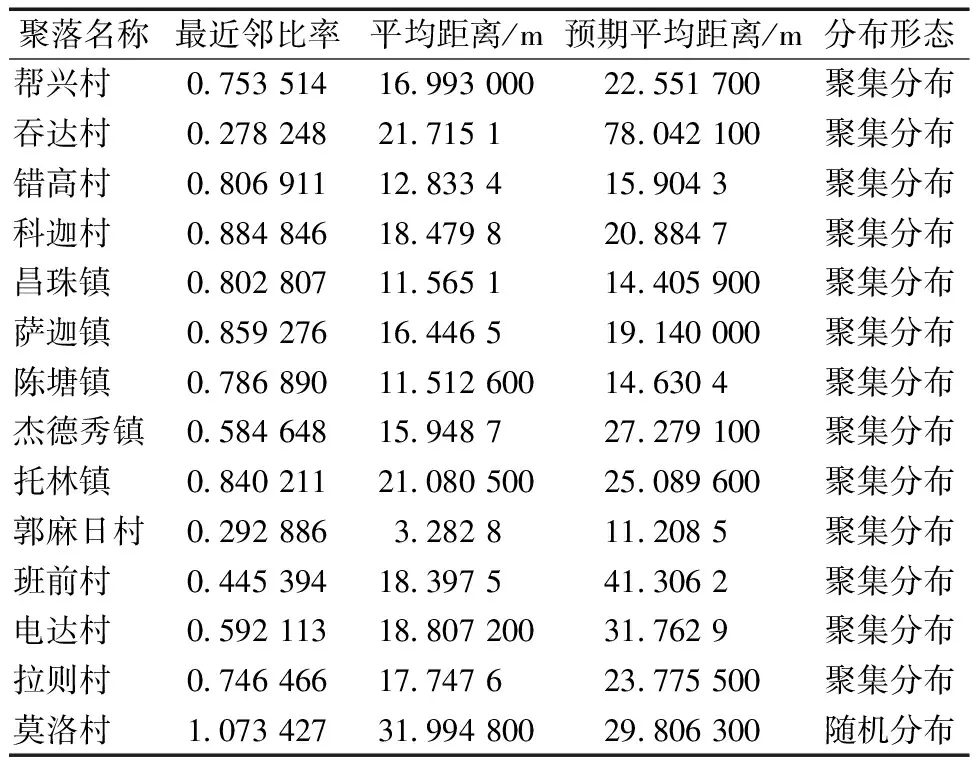
表4 聚落斑块分布形态Table 4 Settlements plaques distribution morphology

从表4的平均最近邻比率可知,除莫洛村的聚落斑块为随机分布外,其余藏族聚落均为聚集分布。

莫洛村建筑斑块呈随机分布的主要原因,是由其特殊的地形和防御需求决定的。在日本学者佐藤方彦等对视域范围的探讨中,描述过这样的规律:7 m是“相互认识域”内的“近接相”范围(3～7 m)与“远方向”范围(7～20 m)的分界点[15]。如表5可知,14个研究对象中,12个聚落的平均最近邻距离在7～30 m这一相对宽阔、但又具备心理安全的范围内。郭麻日村和莫洛村在这范围之外,这和它们的历史背景和原始社会形态有着密不可分的关联,两者都是典型的防御性聚落,但同时又是防御性聚落中不同形态的防御机制。

表5 聚落斑块分布的社会性视域范围Table 5 The social scope of the distribution of settlement plaques

莫洛村建于树木茂密的山坡之上,为躲避战争的侵害,村民上山建屋,修筑烽火碉楼。30 m的距离是能够清晰识别人的面部特征、发型和年纪的极限距离,因此,莫洛村的住居的平均最近邻距离31.995 m意义在于,村民能够在发现外敌入侵的迹象后,为进入碉楼和封锁入口预留时间。藤井明教授在其著作《聚落探访》中提到,离散式布局是村落防御的手段之一,建筑与建筑之间的间隙可作为监测入侵之人的空间,建筑间的间隔一般都会保持在不妨碍视线和声音传播的距离之内[7],莫洛村的分布模式正是如此。而郭麻日村的防御系统则完全相反,郭麻日村建村之初是军屯制社会,地处广袤、相较平坦的环境中。他们筑围墙,成屯堡,走在郭麻日村的古堡中,狭窄悠长的街道空间顿时会让步入其中的人心生戒备,若有外人入侵,不仅会迷失其中,极度局促的空间也让古堡内的人更容易发现外来者的入侵,并进行有效反击[16]。原广司有言:“聚落中看似偶然形成的风格其实都是经过周密计算后而设计的结果。”[17]虽然藏族传统聚落形成于前工业社会,并没有对聚落建筑形态进行规划或设计的方法和概念,但这种“设计”是一种文化潜意识,是融合于民俗风情中潜移默化发生的。

5 结论分析

根据上述研究可知,藏族历史文化村镇聚落建筑斑块所呈现的特征如下:在斑块单体尺度上,藏族聚落建筑斑块的形状与聚落内住居的离散度没有明显的关联;但藏族历史文化村镇的建筑斑块破碎度在一定程度上反映聚落规模,即聚落规模越小,建筑平面越单一,且样式多为简单矩形;反之,聚落建筑平面更具多样化;在斑块整体层面上,藏族聚落建筑斑块整体上呈聚集分布,14个聚落的平均最近邻距离范围的均值约为16.90 m,多数聚落在7～30 m这一尺度范围内并在均值上下浮动。综合两者来看,平均最近邻距离越小的聚落其聚集分布结构越紧凑,建筑斑块密度指数越高,建筑斑块破碎度也越高。

前现代藏族村镇的规模扩张的影响机制中,除地形限制外,最关键的内在因素就是宗教文化。如昌珠镇拥有西藏历史上第一座佛堂——昌珠寺,是文成公主为了镇邪而建造的12个靥胜寺之一[18];萨迦镇的萨迦北寺是藏传佛教的重要教派之一——萨迦派的发祥地[19];杰德秀镇的另一萨迦派名寺——顿布曲果寺[20]和托林镇的托林寺[21]也均是周边信仰文化的中心地之一。这些寺院建筑是影响人口数量的最关键因素,而人口则是聚落扩张的原动力。寺院为聚落固定了最初的原住民,并且源源不断地通过自身的吸引力招聚人群,直至发展为城镇。在村落范畴内,科迦寺、郭麻日寺这些影响力和建造规模较大的寺院所在的村落聚落规模更大一些。纵观研究的全过程可知,藏传佛教文化的影响力越强、越广泛的聚落,其规模越大(斑块数越多)。而聚落规模越大,其对应的民居体量亦越大,且聚落建筑平面更具多样化。

聚落建筑斑块的组织秩序受到地形条件、历史背景、宗教信仰等因素的综合影响。地形方面,如杰德秀镇和班前村,在聚落扩张的过程中为了保护耕地,越过河流和山体,呈现多组团分化组织的模式,班前村的组团数更达8个之多[22]。历史文化背景方面,如吞达村的藏香制作流程[23]、帮兴村的古驿道[24]、郭麻日村的军屯制度[25]、莫洛村的碉楼文化[26]等等都对斑块组织方式有影响。宗教信仰方面,原始苯教文化在藏传佛教文化传入后,影响力逐渐被取代,聚落内原始苯教寺院对聚落结构的影响逐渐退化。14个聚落中只有错高村的圣湖崇拜直接影响到了斑块的分布形态。藏传佛教寺院或寺院建筑群成为影响聚落内建筑组织秩序的主导因素,前面所述的诸多影响因素都统摄于这一主导因素之下,这也是为什么藏族聚落斑块组织形态虽然头绪万千,但仍高度相似地呈现聚集分布的主要原因。每个聚落虽然影响因素各具差异,但宗教文化因素在每个村落中都显而易见,是其共性因素。通过可视化的邻接关系(图5c)可知,集群一般不存在明显的物理性中心,聚集方式也略有不同,但整体上呈现大分散、小聚集的聚集分布状态。

综合前后的结论来看,域内宗教文化影响越衰落的聚落,最近邻比率越高,建筑斑块组织秩序性呈弱化趋势,其斑块的随机性趋势愈大,斑块密度指数和破碎度越低,且斑块形状特征更趋于简单,反之亦然。对比处于相似自然环境下的宗教氛围浓厚的聚落,其聚落建筑组织秩序展现出的明显差别,反映了人文因素是聚落空间格局形成的内生动力。

6 结束语

由于历史文化名村、镇分布地域广泛,各村镇的斑块特征虽具有表象差异性,但是各聚落的形成机制本质上受到文化的深厚影响,仍然呈现出明显的趋同性,聚落斑块的形状和分布特征紧紧联系于藏族社群的共同的宗教信仰和民族文化。换句话说,不同环境下具有相似结构的聚落是源于居住者基于共同文化背景下所形成的相似的空间概念。

藏族历史文化村镇凝聚了藏族同胞千百年的生产和生活记忆,不仅仅是一座座美丽又极具特色的民族聚落,更是其宗教信仰和文化习俗的具象表现。掌握一个民族的聚落营建方式是为新型城镇化发展提供策略,避免“千城一面”的问题屡屡发生的重要途径。在混沌之中探索聚落斑块的核心秩序和文化认同的空间概念,在国家大力推行藏族地区特色村镇建设与新型城镇化建设的大背景下,寻找这一核心秩序以平衡保护和发展的冲突是刻不容缓的。保护地域传统聚落文化的传承与延续,就是保护民族文化和精神文明的基础,这不仅对于藏族传统村镇保护更新、藏族地区特色村镇与新型城镇化建设具有指导性的意义,对世界范围内的建筑文化基因库的形成也意义深远。