数理逻辑中范式推算的程序化研究与实现

杨剑兰，周青

（昆明医科大学海源学院，云南 昆明650106)

0 引言

离散数学是研究有离散结构的系统的学科，譬如，绘制一条直线段的墨水痕迹并非连续，而是由有限多个离散的点组成，这与人类一贯的认知不同。而当计算机打印这条线段时就是以打点的方式打印出来的[1]，因此离散数学思想与计算机工作原理密切关联，并且更加符合万事万物本身的底层特性。其中数理逻辑部分是用符号的方法研究关于命题推理、证明等的问题。丘成桐曾说：“大道至简，是对数学之美的归纳，最简单的数学，从1=1开始，到1+1=2，1+2=3，不停推导下去。人类通过这种方式，认识到自然数，从而有了数学”[2]。因此，在数理逻辑中“逻辑”是一种形式语言，用于表示能得出结论的信息，逻辑问题可转变为由符号与连接词构成的命题公式，并且进一步转换为等价的标准范式，通过标准范式可轻易实现排除错误的逻辑关系、找到符合问题本身逻辑的命题状态，快速达到实现推理和证明出准确结论。

本文针对求解命题公式的主析取范式与主合取范式，在真值表法基础上，分析解释了构造析取（合取）范式时以成真（假）指派反推对应小（大）项的原因，并结合计算机语言程序设计将该解法从理论求解迁移至计算机工具求解，给出了程序设计的具体流程和代码，从而更好地实践“以解决问题为导向掌握和运用工具”学习模式以及帮助学习者建立定理自动化证明的认知，进一步理解人工智能基础。

1 范式

在布尔逻辑中，主析取范式与主合取范式是逻辑公式的标准规范化，其中主析取范式是由各个所涉及命题变元的合取子句即最小项的析取；主合取范式是由各个所涉及命题变元的析取子句即最大项的合取。作为规范形式，它们在自动定理证明中发挥作用，在逻辑问题中将局面直观展现以更清晰地推出结论。比如，以下逻辑谜题：A，B，C，D 四人中要派两人去参加教学比赛，按下述三个条件有几种派法？如何派？

1) 若A去，则C和D中要去一人；

2) B和C不能都去；

3) C去则D留下。

将命题A，B，C，D 分别表示A 参加、B 参加、C 参加、D参加，则该逻辑谜题转换为命题公式：

(A→((C∧¬D)∨(¬C∧D)))∧¬(B∧C)∧(C→¬D)，进一步转化为等价主析取范式并删去与题意矛盾的项目后得到：(¬A∧B∧¬C∧D)∨(A∧¬B∧¬C∧D)∨(A∧¬B∧C∧¬D)，故派法为：B∧D，或A∧D，或A∧C。共三种派法。

2 计算机程序化

2.1 范式连结词与程序逻辑运算符

通过命题公式的等价转换，任何连结词都可转换为：¬（取反），∧（合取），∨（析取）三种最为基本和简单的连结关系，在主析取范式和主合取范式中，规定只能含有以上三种连结词，并且每个符号右边须紧跟单个命题变元。在计算机Java 程序中有三个基本的逻辑运算符与该三个连结词对应，如表1。

表1 命题连结词与对应的Java语言逻辑运算符

当命题公式中含有→（蕴含），↔（当且仅当）连结词时，根据连结词逻辑性质特征，可得出对应的程序语句，如设置前提为P，后件为Q，则P→Q真值符合以下规律：if(!P){(P→Q)=true;}；if(Q){(P→Q)=true;}。P↔Q真值符合以下规律：if(P){if(Q){(P↔Q)=true;}}else{ if(!Q){(P↔Q)=true;} }。

2.2 真值表法求主析取（合取）范式

n 表示命题变元数量，求解主析取范式与主合取范式，利用真值表法可归为以公式成真或成假赋值反推所对应的包含n 个命题变元的各个小项组mi的真值指派问题，为方便观察公式成真和成假时各命题变元的真假状态，范式需包含对所有命题变元的规范整理，在构造主析取范式时：结合析取式的特征，能够使析取式成假的真值指派条件较为苛刻，只有一组m0∨m1∨...mi在等价于F 时可使所有构成析取范式的小项为假，但此时对应的满足为假的小项组太多，为2n-1组，过于烦琐。如命题公式(¬P∧Q)∨¬R，其真值表如表2。

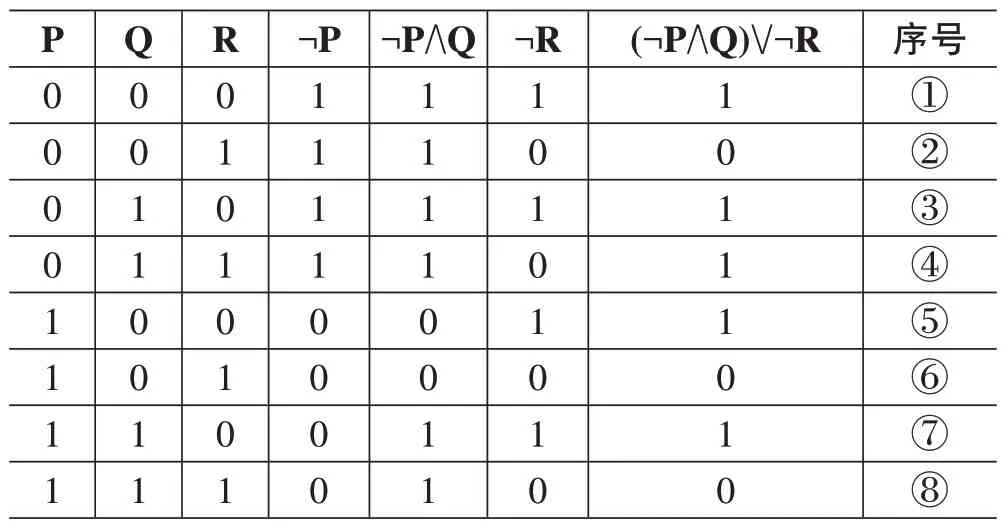
表2 命题公式(¬P∧Q)∨¬R真值表

当(¬P∧Q)∨¬R 为0，对应的P，Q，R 真值指派有3组，为序号②，⑥, ⑧，如：此时序号②对应表3。

表3 (¬P∧Q)∨¬R为0时对应的P，Q，R真值指派组②

此时为1的小项唯有¬P∧¬Q∧R，其余可构造出真值为0的小项23-1=7项，运算量大效率低下；

而当(¬P∧Q)∨¬R 为1，对应的P，Q，R 真值指派有5 组，为序号①，③, ④，⑤，⑦，如：此时序号①对应表4。

表4 (¬P∧Q)∨¬R为1时对应的P，Q，R真值指派组①

根据P、Q、R 三个命题变元的真值指派0、0、0，只可构造出真值为1的小项1项，即¬P∧¬Q∧¬R，除此之外剩余小项23-1=7项为0，运算量小效率高。

因此在构造主析取范式时，采取其真值表中公式成真指派时所对应的最小项的析取式，可反推此时至少有一组所包含的小项值为真，由此精准构造唯一一组对应的小项，将公式所有成真指派时对应的各个唯一小项析取，就能更高效地得到值为真的主析取范式。在构造主合取范式时：结合合取式的特征：能够使合取式成真的真值指派条件较为苛刻，只有一组，在该组真值赋值下，可使所有构成合取范式的大项为真，才能满足使合取范式为真，但大项为真对应的大项组太多，为2n-1组，过于烦琐，因此在构造主析取范式时，采取其真值表中成假指派所对应的最大项的合取式。可反推此时至少有一组所包含的大项值为假，由此精准构造唯一一组对应的大项，将公式所有成假指派时对应的各个唯一大项合取，就能更高效地得到值为假的主合取范式。

基于上述原因，得出定理：

1) 一个公式的真值为T(1) 的指派所对应的小项的析取即为此公式的主析取范式[3]；

2) 一个公式的真值为F(0) 的指派所对应的大项的合取即为此公式的主合取范式[3]。

3 用计算机程序求解命题公式的主析取（合取）范式

3.1 算法思想

1) 统计命题公式的变元数量n，利用多重for循环给出所有n个变元所有真值指派2n个组合；

2) 使用数组保存所有命题变元真值指派下公式的真值；

3) 根据定理，构造主析取（合取）范式。

3.2 对应程序思路

1) 将用户输入的中缀表达式进行for 循环将公式中的字符遍历，并转换为逆波兰表达式用栈来存储；

2) 在逆波兰表达式中判断命题变元的数量；

3) 将n 个命题变元共2n个真值组存储在数组中，循环遍历输出真值表；

4) 求主析取（合取）范式时：当命题公式真值为1(0) 时对应的变元的合取（析取）结果即小（大）项应为成真（假），根据小（大）项性质，应让每一个对应的变元当前值改造为真（假），则若对应变元值为0(1) 输出此变元的非（变元），否则直接输出变元（变元的非），变元与变元之间用合取（析取）连结词连结，项与项之间用析取（合取）联结词连接。

程序核心代码如下：

3.3 上机验证

求解命题公式(¬P∧Q)∨¬R的主析取（合取）范式

在IDEA下运行结果正确，如图1：

图1 Java程序运行结果

4 结束语

符号主义人工智能的思维对应于人类的演绎式思维[4]，而逻辑演绎的符号形式化即数理逻辑，主析取（合取）范式作为数理逻辑中极为有价值的命题公式呈现方式，将包含多个命题变元的公式以满足解读规范的标准连结了各个命题变元与连结词。求解主析取（合取）范式的方法有真值表法以及等值演算法，其中真值表法对应的求解过程更贴合计算机对离散量处理的方式，同时，人类智能本身就是在各个层次上使用符号，如抽象思维、逻辑、语言，因此符号人工智能研究在某种意义上就是对人类理性思维的研究[5]，理解真值表法的求解思路并转换为对应的程序语言对培养人类自身计算思维与认识人工智能都有很大的帮助。