基于改进GAN的断路器线圈电流数据增强方法

杜国庆，石颉

（苏州科技大学 电子与信息工程学院，江苏 苏州 215009)

0 引言

低压断路器是保障低压配电系统安全的关键设备，其健康状态影响着配电系统的性能和稳定性[1]。其中分合闸线圈电流能够很好地反映出低压断路器电磁系统参数变化以及故障的情况[2]。

随着机器学习的不断发展，目前许多机器学习方法都被广泛运用到故障诊断中[3]，而机器学习从不平衡数据中提取的特征往往是不准确的，其判别结果往往趋向于多数类，故不平衡数据集极大限制了机器学习模型对故障的准确诊断[4]。传统对于数据集不平衡的问题，主要通过样本扩充[5]和改良诊断模型[6]两方面。虽然这些方法对不平衡数据集存在的问题做了改进，但还是难以生成逼真的样本数据。

生成对抗网络(Generative Adversarial Networks,Gan) 最初由Goodfellow 等人提出，最近被广泛应用于对输入样本进行学习与训练[7]，为了提高GAN 训练过程的稳定性以及各类别的差异性，本文引入最小二乘损失函数与标签信息，首先通过将损失函数替换为最小二乘损失函数，提高了训练过程的稳定性；其次引入不同类型数据的标签，使得训练出来的数据更符合其标签描述，最后通过皮尔森相关系数、欧几里得距离和余弦相似度验证了生成数据的相似性。

1 理论基础

1.1 生成对抗网络

生成对抗网络的网络结构通常包括生成器与判别器两部分。其中生成器G输入简单的随机噪声，通过学习到与真实样本间的映射关系，输出尽可能真实的样本数据；而判别器D的任务是尽可能判别出生成的样本与真实的样本[8]，其网络结构示意图如图1 所示。通过两者的对抗博弈训练，不断优化各自性能，最后到达纳什平衡[9]。其目标函数公式如下：

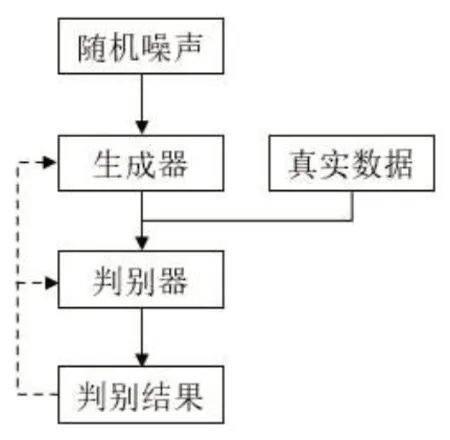
图1 生成对抗网络结构示意图

式中：Pr为真实样本分布，Pz为随机噪声分布，E(·)表示计算期望，G(z)表示生成器生成的样本，D(·)表示判别器输出的结果。

1.2 最小二乘生成对抗网络

原始GAN由于采用交叉熵作为目标函数，在训练过程中可能由于生成样本与真实样本分布差异较大，导致训练过程中出现梯度消失的问题，从而导致生成的数据质量很差。故本文引入最小二乘生成对抗网络(Least Squares Generative Adversarial Networks,LSGAN) ，将GAN 的目标函数由交叉熵改为最小二乘损失函数，解决了梯度易消失以及生成数据质量不高的问题。LSGAN的目标函数如式(2) 所示：

式中：a，b分别为生成样本与真实样本的标签，c是判别器D对生成样本判别为真的期望值，本文设置a=0，b=c=1。

1.3 条件生成对抗网络

原始GAN只能保证生成的数据尽可能真实，但是忽略了生成的数据是否符合对其描述的要求。因此本文引入了条件生成对抗网络(Conditional Generative Adversarial nets, CGAN) ，将对样本描述的条件信息C作为输入，加入网络中进行一起训练，以此来指引GAN 的生成方向，使得生成的样本数据更可控，更符合真实样本规律，其网络结构如图2 所示。CGAN 的目标函数公式如下：

图2 条件生成对抗网络结构示意图

式中：c为标签信息，本文中该标签信息设置为各类故障所对应的标签。

2 实验验证

2.1 基于LSCGAN的数据增强方法流程设计

基于最小二乘条件生成对抗网络的数据增强方法(Least Square Condition Generative Adversarial Networks，LSCGAN) 流程设计主要分为三个环节：1)数据集准备；2)模型训练；3)模型测试。具体步骤描述如下：

1) 将采集的断路器分合闸线圈电流信号随机划分为训练集与测试集。

2) 设计生成器与判别器网络结构，并对模型参数初始化，以最小二乘作为损失函数。首先训练判别器50 次使其具有稍好的判别功能，接着，让生成器与判别器进行对抗博弈训练，使两者达到纳什平衡，此时生成器生成的样本数据达到以假乱真的程度。

3) 使用生成器生成的数据与测试集进行对比，对两者的相似程度进行比较。

2.2 数据集介绍

本文以“CW1-1600”型低压万能式断路器为实验对象，通过NI USB-6002 数据采集卡以50kHz 进行ad采样，使用“CMS0 50NPT”型霍尔电流传感器采集分合闸线圈电流，采集了：0-正常工作；1-动作电压过低；2-合闸线圈老化；3-合闸铁芯空行程过大；4-铁芯卡涩状态下的分合闸线圈电流数据，其中正常工作状态100组，其余4种故障状态各25组，每组波形包含了10 000个采样点，各状态典型电流波形如图3所示。

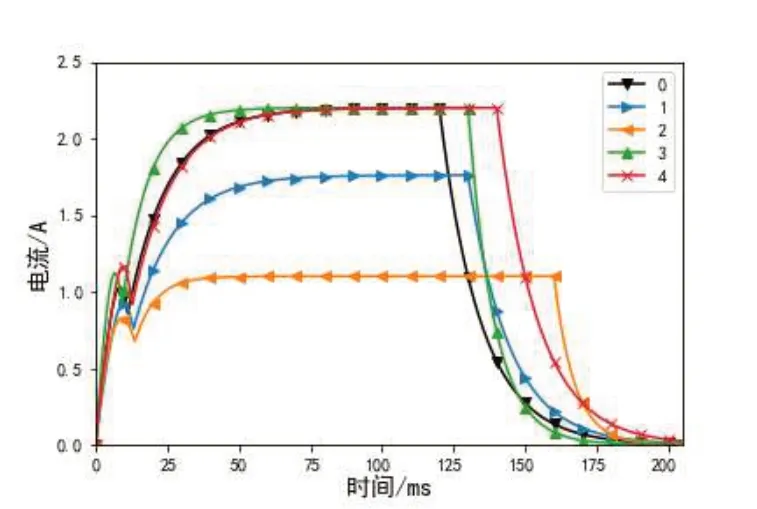
图3 分合闸线圈各状态典型电流图

2.3 评价指标

为了评估生成样本与真实样本的相似性，本文通过皮尔森相关系数、欧几里得距离和余弦相似度三个指标展示生成样本的平均性能。

皮尔森相关系数用于度量两个向量之间的线性相关性，其值介于-1 与1 之间。相关系数越接近于1或-1，相关度越强；相关系数越接近于0，相关度越弱。两个向量间的皮尔森相关系数计算公式如下：

欧几里得距离用于度量m维空间中两个点之间的真实距离，它主要用于评价两个向量在位置上的差异性，其值越小，表示两者相似度越高。两个向量间的欧几里得距离计算公式如下：

余弦相似度将空间中两个向量夹角间的余弦值作为衡量两个个体之间差异的大小，余弦值接近1，夹角趋于0，表明两个向量越相似；余弦值接近于0，夹角趋于90度，表明两个向量越不相似。两个向量间的余弦相似度计算公式如下：

2.4 实验结果

本文实验基于PyTorch 开发环境搭建的网络模型，批处理量设为64，学习率设为0.000 1，迭代次数设为500，并使用SGD优化算法进行优化，训练集与验证集比例划分为7:3。最终训练完成的生成器生成的分合闸线圈各状态电流波形如图4所示。

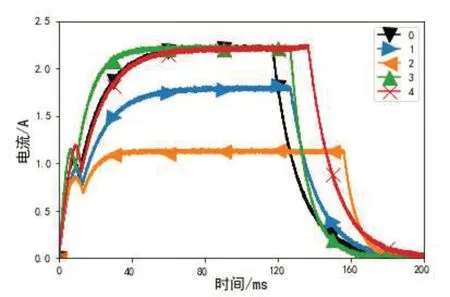
图4 生成分合闸线圈各状态电流图

为验证生成样本与真实样本的相似性，利用生成器生成的样本与测试集通过皮尔森相关系数、欧几里得距离和余弦相似度进行验证，为直观反映出各状态波形的相似性，通过引入混淆矩阵来展示每一个状态的相似程度，其中横轴表示生成样本的类型编号，纵轴表示真实样本的类型编号，如图5所示。从皮尔森相关系数可以看出，同类型生成与真实样本之间的皮尔森相关系数为0.999，而不同类型间的皮尔森系数偏小，说明同类型间的线性相关性较好。通过欧几里得距离可以很明显地看出，同类型间的欧几里得距离最小，且相差较大，说明同类型间的位置差异性较小。通过余弦相似度可以看出，同类型间的余弦相似度最高，说明同类型间的方向差异性较小。由此可见，相同类型的生成样本与真实样本相似度较高，而不同类型间的差异较大，说明本文所提方法可以很好地学习到各类型真实样本的特征与差异，能够较好地完成对不平衡数据集进行扩充及平衡数据集的任务。

图5 生成样本与真实样本相似性相关指标对比

3 结论

本文提出了一种基于改进GAN 的断路器线圈电流数据增强方法，该方法通过最小二乘替换原模型损失函数，提高了模型训练的稳定性；通过加入样本标签信息一起训练，提高了生成模型的可控性。通过皮尔森相关系数、欧几里得距离和余弦相似度这三个相似性指标验证了生成样本质量的可靠性。结果表明，本文所提方法可以作为低压断路器线圈电流数据增强的一种有效手段，具有一定的工程应用价值。