一种球面三自由度并联机构的拓扑与位置分析

李 菊, 王 达, 沈惠平

(常州大学 现代机构学研究中心,江苏 常州 213164, E-mail: wangju0209@163.com)

三自由度球面并联机构是少自由度并联机构的重要分支,由于其具有三维纯转动的独特运动特性,故在卫星天线、机器人肩关节、踝关节等方面有广泛应用[1-6]。

李少帅等[7]基于方位特征集理论,综合了一类三转动输出并联机构;MOURAD等[8]基于位移集李群代数性质的综合方法,研究了非对称无过约束三自由度球面并联机构的结构综合问题;李秦川等[9]对3-P (RR)球面三自由度并联机构进行了运动学分析;HOU 等[10-11]利用遗传算法对3-PSS/S球面并联机构进行了优化设计,明显增大了该机构的姿态工作空间,且提高了其承载能力;CUI等[12]提出了一种三自由度并联机构的新型肩关节,以工作空间最大为目标,建立了肩关节最优结构参数的目标函数;WEI等[13]分析了3-RRR球面并联机构正、逆运动学、静力学,确定了力反馈操作杆静态计算、关节空间和操作空间的力/转矩映射计算方法;HOU等[14]基于螺旋理论,分析了具有同轴输入轴的3-RRR球面并联机构的运动特性;ZHANG等[15]给出了球面3-RRR并联机构的运动传递特性,为球面机构的应用提供了理论依据;文献[16]研究了一类特殊球面三自由度并联机器人的奇异轨迹;文献[17]提出了一种减少杆件间干涉的设计方法,以增加球面机构的工作空间。

一般地,求解球面并联机构的位置正解较为复杂,需较好的数学知识,如:利用四元数代数求解球面机构位置正解[18]。

1 机构的拓扑结构分析

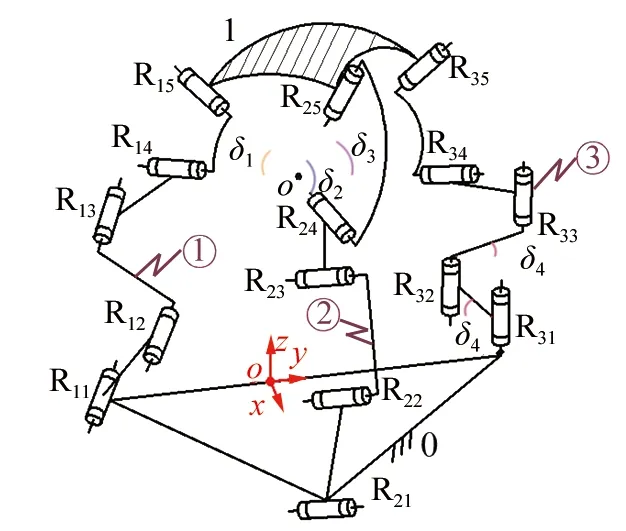
▲图球面并联机构

为使设计、制造方便,取转动副Ri1(i=1～3)的轴线分别与静坐标系的X、Y、Z轴平行,并分别作其轴线的垂直平面,如图2所示。

上述3个垂直平面相交于一点,而3个转动副Ri4(1～3)的轴线也相交于一点,因转动副Ri4(i=1～3)的轴线被布置于Ri1(i=1～3)轴线的垂直平面内,因此上述两交点重合,即转动中心o的位置可仅由3条支链的运动平面确定。进一步,垂直于X轴的运动平面(①支链运动平面)与垂直于Y轴的运动平面(②支链运动平面)两者的交线决定了转动中心o所在Z轴在XOY平面上的位置,而垂直于Z轴的运动平面(③支链运动平面)决定了转动中心o在Z轴上的高度,如图2所示。

因此,通过对Ri4(i=1～3)轴线的布置,易确定动平台的转动中心点o。而转动副Ri4(i=1～3)距离转动中心点o的距离,即球面运动的半径,可以根据机构的工作要求来确定。

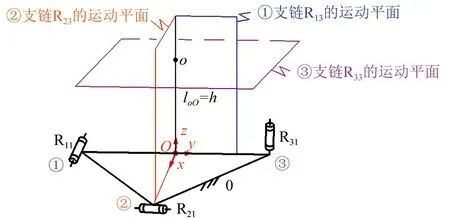
▲图2 点o位置的确定

2 机构的拓扑特征分析

2.1 机构的POC集

(1) 并联机构的POC方程[19]为

(1)

(2)

式中:MJi—第i个运动副的POC集;Mbi—第i条支链末端的POC集;MPa—机构动平台的POC集。

(2) 机构的POC集

选取动平台1外的球心点o为基点。

① 各支链的拓扑结构分别为

② 确定支链末端构件的POC集。

支链末端构件POC集,由式(1)得,

③ 确定动平台的POC集,由式(2)得

因此,动平台1具有绕点o作三维转动的输出特性。

2.2 机构自由度

(1) 并联机构的全周DOF公式为

(3)

(4)

(2) 确定本机构的DOF

① 确定独立位移方程数

由第①、②支链构成的第1回路(即子并联机构)的独立位移方程数,由式(3)得

该子并联机构的自由度,由式(4)得

由上述子并联机构和第③支链构成的第2回路的独立位移方程数,由式(3)得

(2) 确定机构自由度,由式(4)得

故当取静平台0的3个转动副R11,R21,R31为驱动副时,动平台1可实现绕点o的三维转动输出运动。

2.3 机构耦合度

(1) 基本理论

由基于序单开链(SOC,Single-open-chain)的机构组成原理知,任一机构可分解为约束度为正、零、负的3种有序单开链(SOC),第j个SOCj的约束度定义为

(5)

式中:mj—第j个SOCj的运动副数;Ij—第j个SOCj的驱动副数。

进一步,一组有序的v个SOC可组成1个独立回路数为v的(最小)子运动链SKC (Sub-kinematics chain),SKC的耦合度为

(6)

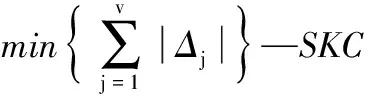
(2) 确定本机构的耦合度

2.2节中,已计算出2个回路的独立位移方程数,即ξL1=6,ξL2=6。由式(5)得,它们的约束度分别为

显然,由第1、2回路构成1个SKC,由式(6)得,该SKC的耦合度为

即该机构只包含1个SKC,其耦合度k=2,因此,理论上需设2个虚拟变量。

3 机构的位置分析

3.1 坐标系建立及参数标注

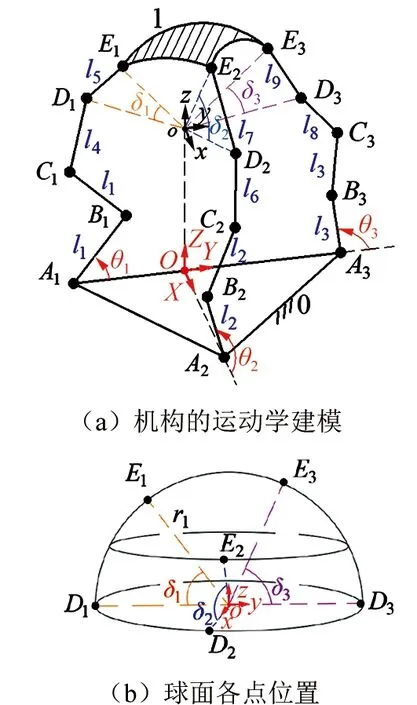
为便于分析,将图1所示并联机构简化为图3(a)所示运动学模型。

▲图球面机构的运动学建模

设静平台0为等腰直角三角形,其外接圆半径为r0,静坐标系O-XYZ的原点设在斜边A1A3的中点处,X轴沿OA2方向,Y轴沿OA3方向,Z轴由右手螺旋法则确定。静平台上各顶点A1、A2、A3所对应的转动副R11、R21、R31的轴线分别与静坐标系的X、Y、Z轴平行。

设动平台1为球面,动坐标系o-xyz的原点设在其球心o处,动坐标系o-xyz由静坐标O-XYZ沿Z轴正方向平移距离h得到(根据图2的分析,h值可由R33的Z轴坐标确定);球面上点Di、Ei(i=1～3)到球心o的距离为r1,其位置如图3(b)所示;点Di、Ei所对应的转动副Ri4和Ri5(i=1～3)的轴线间的固定夹角为δi(i=1～3),CiDi为转动副Ri3(Ci)和Ri4(Di)轴线的公垂线(i=1～3),如图3(a)所示。

第③条支链中,转动副R31和R32的连杆、R32和R33的连杆与水平面的固定夹角都为δ4,如图1所示;各杆长为li(i=1～9),如图3(a)所示。

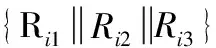
设驱动副R11、R21、R31绕各轴的输入转角分别为θ1、θ2、θ3,如图3(a)所示;而动平台1绕X、Y、Z轴的输出转角分别为α,β,γ。

▲图4 点D1、D2、D3运动轨迹示意图

3.2 基于拓扑特征的机构位置正解求解方法

由2.3节可知,该机构包含1个SKC,该SKC可分解为约束度值分别为Δ1=+2、Δ2=-2的两种单开链,因此,该机构位置正解的求解,可转换为该SKC内两种单开链回路的位置求解,具体为:第1回路的约束度Δ1=+2,理论上需设2个虚拟变量,例如动平台的输出变量α和β(而输出变量γ为虚拟变量α和β的函数表达式),并在约束度Δ2=-2的第2回路中建立约束方程,然后使用二维搜索法求得α、β的值,进一步求得γ的值。

但由于球面机构的三个输出转角α、β、γ之间的强耦合关系(k=2),通过第1回路的计算,发现γ关于α和β的函数表达式极其复杂,不利于进一步的计算,因此,将原作为中间变量的γ也设为虚拟变量,即设立α、β、γ三个虚拟变量,并在约束度为-2的第2回路上建立关于虚拟变量α、β、γ的3个约束方程,然后通过三维搜索法求得该机构的位置正解。

3.3 位置正解求解

已知:3个主动副R11、R21、R31的输入转角分别为θ1、θ2、θ3,求:动平台1绕坐标系O-XYZ输出转角α、β、γ。

3.3.1 SKC1位置求解

第1回路A1-B1-C1-D1-E1-A2-B2-C2-D2-E2点的坐标

易知,A1=(0,-r0,0),A2=(r0,0,0),B1=(0,-r0+l1cosθ1,l1sinθ1),B2=(r0+l2cosθ2,0,l2sinθ2),o=(0,0,h)。

设动平台1绕X、Y、Z轴的输出转角分别为α,β,γ,则旋转矩阵为Q为

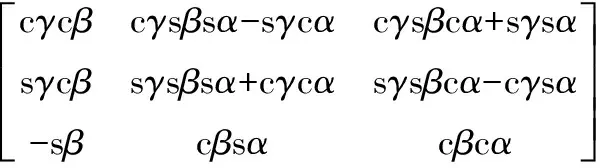
式中:s、c分别表示sin、cos。

点D1的运动轨迹是以点o圆心,半径为r1的圆形如图4(a)所示,故D1点坐标表示为:D1=(0,r1cosφ1,h+r1sinφ1)。

由杆长约束条件D1E1=l5,可解得φ1为关于α,β,γ的表达式

(7)

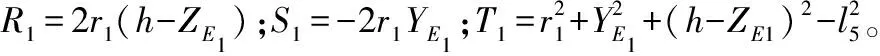
于是,由点D1坐标,根据C1D1⊥D1o的几何条件,可进一步求得C1点坐标:C1=(0,YD1-l4sinφ1,ZD1+l4cosφ1)。

再由杆长约束条件B1C1=l1,得到包含θ1,α,β,γ的表达式,

f1(θ1,α,β,γ)=0

(8)

点D2的运动轨迹是以点o圆心、半径为r1的圆形,如图4(b)所示,故D2点的坐标表示为:D2=(r1cosφ2,0,r1sinφ2+h)。

由杆长约束条件D2E2=l7,可解得φ2关于α,β,γ的表达式为

(9)

于是,由点D2坐标,根据C2D2⊥D2o的几何条件,可进一步求得C2点坐标:C2=(XD2+l6sinφ2,0,ZD2-l6cosφ2)。

再由杆长约束条件B2C2=l2,得到包含θ2,α,β,γ的表达式

f1(θ2,α,β,γ) =0

(10)

3.3.2 SKC2位置求解

第2回路A3-B3-C3-D3-E3各点的坐标

易知,A3=(0,r0,0),B3=(-l3cosδ4sinθ3,r0+l3cosδ4cosθ3,l3sinδ4)。

点D3的运动轨迹是以点o圆心、半径为r1的圆形,如图4(c)所示,故D3点的坐标表示为:D3=(r1sinφ3,r1cosφ3,h)。

由杆长约束条件D3E3=l9,可解得φ3关于α,β,γ的表达式

(11)

于是,由点D3坐标,根据C3D3⊥D3o的几何条件,可进一步求得C3点坐标为:C3=(XD3+l8cosφ3,YD3-l8sinφ3,h)。

再由杆长约束条件B3C3=l3,得到包含θ3,α,β,γ的表达式

f3(θ3,α,β,γ) =0

(12)

联立式(8)、(10)、(12),得到三元一次非线性三角方程组,代入已知的输入角度θ1、θ2、θ3,通过三维搜索法得到输出角度α、β、γ值。

3.4 位置反解求解

已知动平台1的三个输出转角α,β,γ,求静平台上3个驱动副R11、R21、R31的输入转角θ1、θ2、θ3。

由式(8)可解得

(13)

其中:U1=-2l1ZC1

V1=-2l1(Yc1+r0)

由式(10)可解得

(14)

其中:U2=-2l2ZC2

V2=-2l2(Xc2-r0)

由式(12)可解得

(15)

其中:U3=2l3XC3cosδ4

V3=2(r0-YC3)l3cosδ4

根据机构位置正解与反解的对比,可知,该耦合度为2的球面机构输出转角参数的强耦合关系,是造成其位置正解难求的重要原因。

4 实例验算

4.1 正解算例

设该机构的结构参数为:r1=30,r0=60,h=40;l1=50、l2=50、l3=40、l4=40、l5=30、l6=40、l7=30、l8=20、l9=30(单位:mm);δ1=δ2=δ3=60°、δ4=30°。

设3个主动副R11、R21、R31的转动角度为:θ1=78.418 2°,θ2=139.665 4°,θ3=130.413 1°,将其代入式(8)、(10)、(12)组成的三元一次非线性方程组,运用Matlab编程,对α、β、γ进行三维搜索,搜索范围为:-180°<α<180°、-180°<β<180°、-180°<γ<180°,求得α,β,γ的两组解,如表1所示。

表1 位置正解/(°)

4.2 反解算例

将表1的No.1*的α,β,γ数值代入式(13)、(14)、(15),求得θ1的实数解为:78.418 2°、-69.685 7°、73.932 7°、52.169 6°,θ2的实数解为:139.665 4°、84.166 1°、-105.196 7°、115.944 3°,θ3的实数解为130.413 1°、-94.017 9°、-115.769 4°、-174.517 4°,则机构位置反解共有4×4×4=64组,如表2所示。

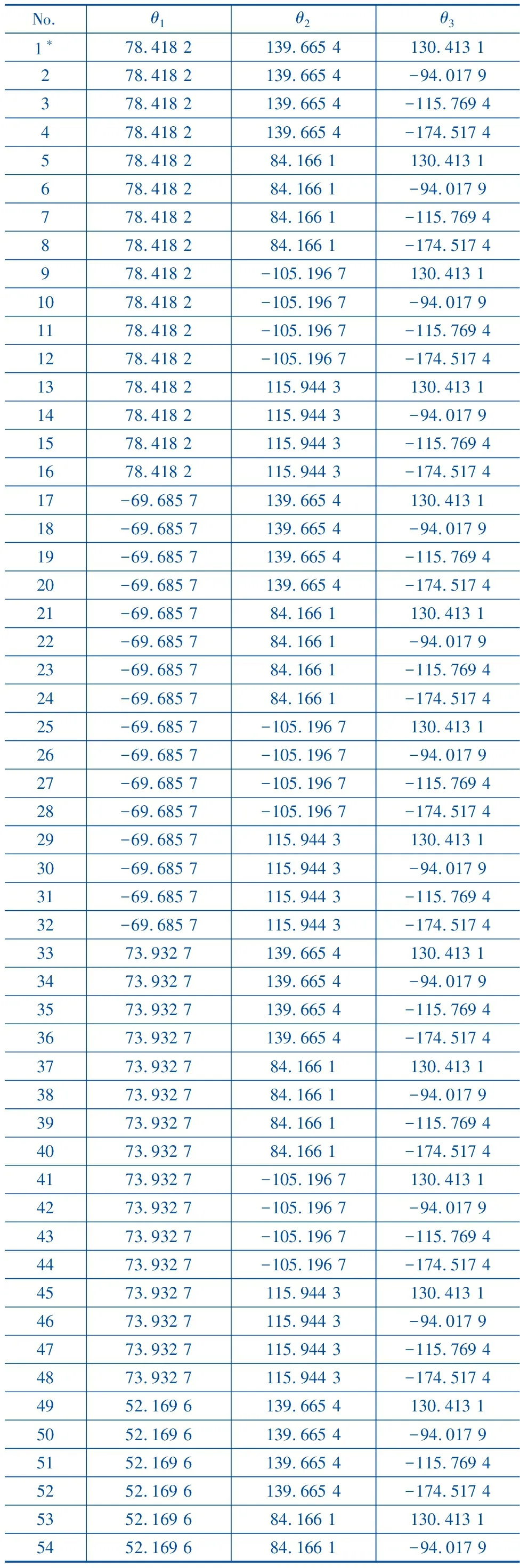
表2 位置反解/(°)

表2中的No.1*组解与正解计算给定的3个主动副输入角θ1=78.418 2°,θ2=139.665 4°,θ3=130.413 1°一致,故机构的位置正、逆解公式推导正确。

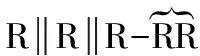
该球面机构可用于航空、新能源技术、机械加工、医疗等领域,如卫星定向装置、太阳跟踪装置、机械加工的回转工作台和零件定位装置、康复装置等,特别可用于制作踝关节的康复、训练等装置,具有较好的应用前景。

5 结论

(1) 对三自由度球面机构进行了拓扑结构分析,表明动平台围绕定点o作纯转动运动,点o的位置由三条支链的装配位置所决定,这为该机构的结构设计提供了依据。

(2) 对该球面机构的三个重要拓扑特征进行了分析,表明该机构是一个三自由度的三转动输出机构,其耦合度为2。

(3) 运用基于拓扑特征的机构位置分析方法求解了该球面机构的位置正逆解,求解过程简明,为复杂球面机构的位置分析提供了一种可行的思路。