数控机床几何误差的雅克比旋量建模
2023-07-25陈坤,刘顺,金隼
陈 坤, 刘 顺, 金 隼
(上海交通大学 上海市复杂薄板结构数字化制造重点实验室,上海 200240,E-mail: scu90ck@163.com)
提高机床精度是高端数控机床产品研发的目标,也是我国机床行业亟需加快突破的核心技术挑战之一。几何误差和热误差是导致机床精度损失的最重要因素[1-2],由于几何误差具有重复性、可测量性和稳定性[3],因此减小几何误差是提高机床精度最经济有效的方法之一。机床几何误差是指机床设计、制造导致的机床中各组成环节或部件的实际几何参数和位置相对于理想值发生偏离的误差,以五轴数控机床为例,其几何误差包含有位置度、直线度、角度等41项,其产生、传递和作用机理复杂。机床几何误差正向设计时依据机床检测标准和工程经验对各轴精度进行“靠近式”设计,零件制造装配后,对机床几何误差进行检测,对超差部分进行“修配”,使其精度达到检测要求。这种依靠经验式的设计与装配,由于缺乏零部件误差与机床几何误差映射关系的理论指导,无法对几何误差进行源头追溯与量化处理,前期设计时对公差赋值科学性不强,导致修配的工作量大,装配周期长。
目前以国标为设计准则的机床设计标准,仅仅规定了机床几何误差的检测标准,并未对几何误差的设计做出指导。为了对机床几何误差进行优化,必须要建立几何误差的参数化模型,建立几何误差与零部件误差的关联关系,通过建立几何误差的约束方程,获得几何误差的变动范围。雅可比旋量模型综合运用了适合公差传递的雅克比矩阵及适合公差表达的旋量模型,能够对三维空间内的公差传递进行表达与求解。陈华[4]利用雅克比旋量模型进行发动机装配过程的优化,提高了发动机装配精度与效率;丁司懿[5]针对航空发动机多级转子堆叠装配的特点,基于雅可比旋量模型提出了主副基准的概念,并提出了转子堆叠的优化装配方法;杜正春等[6]将此模型应用在机床装配中,用于确定机械零件中的关键误差如何影响和累积到综合误差,并对相关特征进行了敏感性分析。黄杰等[7]针对机床制造和装配过程中产生的几何误差, 提出了基于旋量理论的数控机床几何误差分离与补偿方法。以上这些研究说明了利用雅克比旋量模型进行公差分析的适用性和有效性。
本文针对数控机床几何误差设计缺乏理论指导,无法建立几何误差与机床零部件误差映射关系的现状,建立了基于雅克比旋量模型的数控机床几何误差的参数化模型,对几何误差的影响因素进行分析溯源,为机床几何误差设计与调整提供了理论指导。
1 雅克比旋量模型
雅克比矩阵来源于机器人运动学,用于机器人各关节位姿与速度、加速度等参数的传递与计算,Laperrière和Lafond[8-9]将公差特征中的传递路径视为虚拟关节,将雅可比矩阵引入到装配体的公差传递中,这样可以用来计算功能要求在公差域中的变动,其矩阵表达式为:
(1)

(2)
其中:dxin=dxn-dxi,dyin=dyn-dyi,dzin=dzn-dzi。

▲图1 旋量模型示意图
旋量理论(Torsor Theory)最初是被用来描述物体的位姿变换,物体的任意位姿变动都可以分解为一个绕某一直线的平动和绕该直线的转动,因此这种运动又被称为螺旋运动[10]。后来Clément[11-13]将该理论应用到公差模型的表达中,用一组沿着坐标轴移动的矢量ε和一组绕着坐标轴转动的矢量ρ以对特征在公差域内的变动进行表达,如图1所示。
S0为特征理论值,S1为特征在公差范围内的变动值,那么变动值S1相对理论值S0的波动范围为T,变动后的特征S1相对变动前的特征S0的旋量表达为:
(3)
式中:α、β与γ是绕坐标轴的三个转动矢量,u、v和w为沿着坐标轴移动的三个移动矢量。此旋量表达了特征在公差域内的波动范围,只要对旋量内的变动矢量加以限制,即是对特征公差加以限制,这样就建立了旋量内矢量波动范围与特征公差波动范围的关联性。
雅克比旋量模型是由Desrochers等[14]提出的,该模型将适用于公差传递的雅可比矩阵模型与适合公差表达的旋量模型相结合,非常适合域三维公差分析与求解,近些年也受到研究者的广泛关注。其模型表达为:
(4)
式中:方程左边为功能需求特征的旋量表达,方程右边为功能特征的雅可比矩阵与功能特征的旋量表达。
2 数控机床几何误差的雅克比旋量建模
以五轴机床为例,其每个轴有几何误差6项,三个移动轴之间有垂直度误差3项,加上每个回转轴垂直度误差2项、位置度误差2项,共计41项几何误差。
2.1 运动轴轴内几何误差的建模
根据ISO 230-1[15]对几何误差给出的定义,以Z轴为例,直线轴的6项误差分别是εzz-Z轴的定位误差,εyz-Y轴方向上的直线度误差,εxz-X轴方向上的直线度误差,δzz-绕Z轴回转的角度误差(滚转误差),δyz-绕Y轴回转的角度误差(俯仰误差),δxz-绕X轴回转的角度误差(偏摆误差)。在J-T模型中,解决的是尺寸链中功能需求特征在基准坐标系下的位姿变动。机床床身工作台简图如图2所示。

▲图2 数控机床X轴示意图
工作台运动方向为Z方向,根据运动J-T模型的求解流程,功能需求为上方工作台相对床身坐标系的位姿变动,其表达为
(5)
2.2 运动轴轴间几何误差的建模

▲图3 J-T模型下垂直度几何误差的对应
对于轴间的几何误差,以X轴与Y轴间的轴间误差Sxy为例进行讨论,如图3所示。
机床X轴与Y轴均固定在基座上,机床的X轴运动依靠X轴滑块在X轴导轨上的滑动,机床Y轴运动依靠Y轴滑块在Y轴导轨上的滑动,X轴导轨滑块及其上的附属部件形成X轴的六项几何误差,Y轴导轨滑块及其上的附属部件形成Y轴的六项几何误差。
以X轴导轨为基准,Y轴导轨相对X轴导轨的位姿变动构成了Y轴相对于X轴的几何误差,根据J-T模型的求解流程,功能需求为Y轴导轨相对于X轴导轨坐标系的位姿变动,其表达为
(6)

▲图4 J-T模型下X与Y轴垂直度几何误差的对应
根据X轴与Y轴之间垂直度的定义,以X轴为基准,Y轴与X轴之间实际角度与直角的差异,反映在J-T模型中,即是Y轴导轨相对X轴导轨的绕Z轴旋转,即对应上式γ角,如图4所示。
由图4示可以看出,Y轴导轨相对X轴导轨的γ转角即是X轴与Y轴间的垂直度误差,只需建立二轴的J-T模型获取Y轴导轨相对于X轴导轨坐标系的位姿变动,就可以对Sxy的波动范围进行表达。同理,对于Y轴与Z轴间的垂直度误差Syz,只需建立Y轴与Z轴的J-T模型获取Z轴导轨相对于Y轴导轨坐标系的位姿变动中的α转角波动范围;对于X轴与Z轴间的垂直度误差Sxz,只需建立X轴与Z轴的J-T模型获取Z轴导轨相对于X轴导轨坐标系的位姿变动中的β转角波动范围,即可实现直线轴三个垂直度误差的对应。
由此可见,通过遴选基准坐标与目标点,基于雅可比旋量模型建立其描述方程,可以构造所有几何误差的参数化表达。通过雅克比旋量模型进行机床几何误差参数化表达的关键在于确定基准坐标系与特征需求。
3 实验验证
本节以某公司某型号数控机床的εxz(Z轴方向上的X向直线度误差)为例,对本文提出的基于雅克比旋量模型的几何误差参数化表达方法的有效性进行说明,同时对其表达的精确性进行验证。仍以图2所示的卧式机床Z轴装配体为例进行说明,机床Z轴零部件的尺寸图见图5所示,尺寸表见表1,特征需求为滑块上表面相对于床身坐标系的位姿变动。
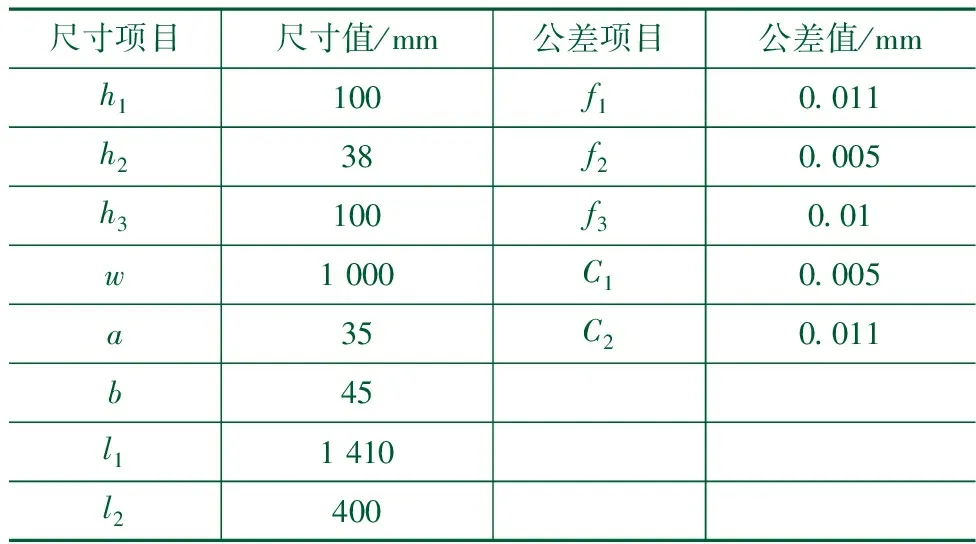
表1 Z轴装配体尺寸表

▲图5 Z轴装配零部件尺寸图
根据机床Z轴拓扑结构,零部件装配形式及公差,可得到机床Z轴相关功能元素的运动雅可比矩阵和相关特征旋量的表达如表2所示。

表2 数控机床Z轴子装配功能元素的雅可比矩阵及旋量
根据表2可知,滑块上表面相对床身底面坐标系的位姿变换的FR(功能需求)表达式为
(7)
此处εxz对应旋量表达中的v分量,带入雅可比矩阵与旋量数据,得
v∈[0,0.014]
(8)
依据6σ原则,
εxz∈[0.004 7,0.009 3]
(9)

▲图6 数控机床εxz几何误差的测量
为了对模型结果进行验证,对某公司PT50五台机床的εxz进行测量,如图6所示。在工作台上置检测板,主轴上置千分表,千分表指针顶住检测板右侧面,工作台沿Z轴运动,千分表的示数波动量即是Z轴的X向误差,测量结果与模型结果的对比如图7所示。

▲图7 雅可比矩阵模型参数化εxz与实验测量的比对
由实验与模型对比可以看出,实验测量的机床几何误差均在通过雅可比旋量模型参数化获得的几何误差的公差范围内,证明了通过雅可比旋量模型对几何误差进行参数化表达的有效性,为后续通过雅可比旋量模型对几何误差的传递建模打下了基础。
