水源含沙喷灌对折射式喷头冲蚀磨损规律研究

2023-07-25李俊龙张以升

节水灌溉 2023年7期

李俊龙，李杰，张以升

（郑州大学水利与土木工程学院，郑州 450001）

0 引言

黄河流域是我国重要的粮食基地，农业用水占比大，推广实施滴灌和喷灌等农业节水技术是促进黄河流域生态保护和高质量发展的有效途径[1,2]。由于滴灌系统对水质要求较高，实施引黄滴灌对灌溉系统首部过滤装置要求较高，将增大系统成本的投入。与滴灌相比，喷灌对水质要求不高，实施引黄喷灌时不易堵塞，适用性较强[3,4]。然而，喷头作为喷灌系统中易受损毁部件之一，在喷灌过程中，黄河水中的泥沙颗粒会对喷头产生冲蚀磨损进而影响使用寿命和水力性能。因此，研究含沙水源条件下折射式喷头的冲蚀磨损规律具有重要意义。

近年来，喷头的冲蚀问题逐渐受到国内外关注。Giles等[5-7]通过对不同材料制造的喷头在工作一定时间后的结构变化进行研究，对比分析了喷嘴的冲蚀磨损情况；Krishnan 等[8]根据试验结果得出了喷头冲蚀率的经验公式，并建立了失效标准；李红等[9,10]通过试验的方法观察喷嘴尺寸的变化从而判断磨损的程度，研究了冲蚀对喷头可靠性的影响；李英能等[11]通过开展不同工况下喷头冲磨试验，分析了各因素与喷头冲蚀之间的关系；翟恩昱等[12,13]通过建立固体颗粒的运动方程对冲蚀情况进行理论分析，根据试验结果验证并确定了颗粒冲蚀喷头内表面时的速度。以上相关研究通过试验或理论分析的方法对全射流喷头的结构优化及扇形雾喷头的冲蚀变形进行了分析，为喷灌喷头的安全运行提供了借鉴，但却忽略了冲蚀磨损对喷头内部结构及其水力性能的影响。

随着计算机性能的提升和数值仿真软件的日趋成熟，采用数值仿真的方法模拟喷头的冲蚀情况可有效降低试验成本。因此，部分学者通过数值模拟方法对喷头的冲蚀规律进行了研究。Zheng 等[14]运用CFD 软件对高压喷嘴的颗粒射流过程进行数值模拟，研究并分析了射流时的固体颗粒加速度和运动轨迹，为提高其工作效率提供参考；Du 等[15]建立了从磨料颗粒进入喷嘴到冲击工件的全过程仿真模型并研究了喷嘴的磨损模式；田家林等[16]利用仿真软件模拟了不同类型喷头含颗粒时的冲蚀磨损情况，并分析仿真结果确定了射流效果最好的喷头类型；申恒峰等[17]基于冲蚀耦合动网格的方法对摇臂式喷头进行分析，得出了冲蚀磨损的规律。以上研究利用数值仿真的方法分析了喷头的冲蚀情况，为进一步研究不同工况下折射式喷头的冲蚀位置及规律提供了一种可靠的模拟思路。

折射式喷头具有工作压力低、抗风性能好等优点，被广泛应用于喷灌方面[18,19]。以往研究多集中于全射流喷头和摇臂式喷头的结构优化与冲蚀规律，对折射式喷头冲蚀磨损方面的研究较少。因此，本文通过室内试验与数值仿真的方法对折射式喷头冲蚀过程进行分析，确定了该类型喷头的冲蚀位置及冲蚀速率，为研究喷头的冲蚀规律与失效预测提供参考依据。

1 材料与方法

1.1 试验设置

1.1.1 试验材料

试验所采用的折射式喷头型号为Nelson D3000（Nelson Irrigation Corporation，Walla Walla，Washington），主要由红色喷嘴和蓝色喷盘组成，结构如图1所示[20]。红色喷嘴的直径为4.76 mm，蓝色喷盘的直径为31 mm，其中心处有一个高度为2.8 mm 的圆锥体，喷盘上带有3 个分水台和36 个流道。当喷头组装完成后，喷嘴位于喷盘上方12.5 mm 处。在使用期间，水流经喷嘴喷射到蓝色喷盘上，并分成36 股射流沿流道向四周射出。

图1 试验所用的Nelson D3000喷头Fig.1 Nelson D3000 sprinkler used in the experiment

1.1.2 试验方法

折射式喷头冲蚀试验在郑州大学水力学试验室进行。试验装置如图2 所示，主要由增压泵、PVC 管道、压力传感器、搅拌器、塑料搅拌桶、支架及阀门等设备组成。塑料搅拌桶的直径和高度分别为1.0 m和1.3 m；在搅拌桶的上方安装电机功率为1.1 kW的搅拌器，搅拌速度可调。

图2 折射式喷头冲蚀试验布置Fig.2 Erosive test arrangement of refraction sprinkler

喷头的工作压力由压力传感器（西安云仪SLK800T）测量，其范围为0～500 kPa，精度为0.1%。试验所采用的黄河沙密度为2 650 kg/m³。试验在含沙量为1%，进口流速分别为9.87 m/s （50 kPa）、13.69 m/s （100 kPa）、16.75 m/s （150 kPa）、19.42 m/s（200 kPa）和21.65 m/s（250 kPa）的工作条件下进行[20]。冲蚀时间为48 h，利用3DScanner 软件及仪器对冲蚀前以及冲蚀一定时间后的蓝色喷盘进行扫描还原，通过Geomagic Studio 2014 软件处理数据，得出锥角高度、流道长度以及喷盘质量的变化等，从而计算喷头的冲蚀速率。

1.2 数值模拟

1.2.1 数学模型

（1）控制方程。流体计算是冲蚀计算的基础，文章采用的N-S方程如下：

式中：ρ为流体密度，kg/m3；为瞬时速度矢量，m/s；p为压力，Pa；为应力张量；ρg为重力，N；为颗粒相对连续相作用的附加源项。

文章采用的标准k-ε模型如下：

式中：Gk为由平均速度梯度产生的湍流动能；ε为湍流耗散率；ui为i方向上的流体速度，m/s；k为湍流动能；xi、xj为空间坐标；εk、εε分别为k、ε对应的普朗特数，取值分别为1.0、1.3[21]；Sk、Sε为源项；C1ε、C2ε为经验常数，取值分别为1.44、1.92[21]。

（2）离散相模型。对于固液两相流，固体颗粒的体积分数相对较小，可作为离散相处理，能够忽略颗粒之间的相互碰撞和剪切应力的影响[22,23]。根据牛顿第二定律，质点的运动控制方程如下：

（3）冲蚀模型。本文采用Fluent中所定义的冲蚀模型[24]对折射式喷头进行模拟计算。冲蚀速率的计算公式如下：

式中：E为冲蚀速率，kg/（m2·s）；N为颗粒数量；mp为颗粒质量流率，kg/s；C(dp)为颗粒直径函数，取为1.8 × 10-9；f(α)为冲击角函数；v为颗粒的相对速度，m/s；b(v)为相对速度函数；Aface为计算单元的面积，m2。

冲击角函数采用分段线性函数[25]进行拟合，取值如表1所示。

表1 冲击角Tab.1 Impact angle

恢复系数是当固体颗粒与管壁发生碰撞时，碰撞前后速度分量的比值。恢复系数的改变是因为存在能量转移和能量损失，文章取值如下[26]：

1.2.2 网格划分

根据喷头结构采用SolidWorks软件建立了流体域的三维模型。利用ANSYS ICEM 软件对几何模型进行网格划分，网格类型采用非结构化网格。以喷头的冲蚀速率作为衡量网格准确性的依据，进行网格的无关性检验，确定网格数量为1 565 276。在数值模拟过程中，进口设置为速度进口，出口设置为标准压力出口，颗粒作用于壁面的类型设置为Reflect。模型的网格划分及边界条件如图3所示。

图3 模型的网格划分及边界条件Fig.3 Mesh division and boundary conditions of the model

1.2.3 求解方法

本次研究采用VOF 模型和DPM 模型进行计算，选择SIMPLE 算法来求解压力、速度的耦合方程，选取二阶迎风格式对动量、湍流动能和湍流耗散率进行离散。重力和工作压力分别设定为9.81 m/s2和101 325 Pa。所有方程的时间步长设置为0.001 s，时间步数为10 000步，总时长为10 s，收敛精度设置为0.000 1。

2 结果与分析

2.1 试验与模拟的对比分析

图4 为蓝色喷盘的冲蚀过程，从图4 中可以看出，随着喷灌历时的增加，喷盘的表面结构发生显著变化：锥角直径逐渐增大，锥角高度不断下降，流道长度和分水台长度逐渐减小，表明冲蚀主要发生在喷盘锥角、流道与分水台凸起处等几个部位。

图4 蓝色喷盘冲蚀过程Fig.4 Blue jet plate erosion process

通过数值模拟得到喷盘的冲蚀云图与试验结果对比如图5所示。从冲蚀云图中可以看出，该类型喷头的冲蚀区域主要集中在喷盘的锥角、流道与分水台凸起位置处，与试验冲蚀位置一致。

图5 试验与数值模拟冲蚀位置对比Fig.5 Comparison of experimental and numerical erosion positions

固体颗粒在流体的影响下以较高的冲击速度与材料表面发生碰撞，进而形成严重的冲击磨蚀，折射式喷头壁面的冲蚀程度可用冲蚀速率[27]定义，表示单位时间内固体颗粒对壁面材料的切削剥离质量。表2 为试验与数值模拟冲蚀速率的对比，从表2中可以看出二者偏差小于3%，具有良好的吻合性，进一步验证了该数值模拟方法的可靠性。

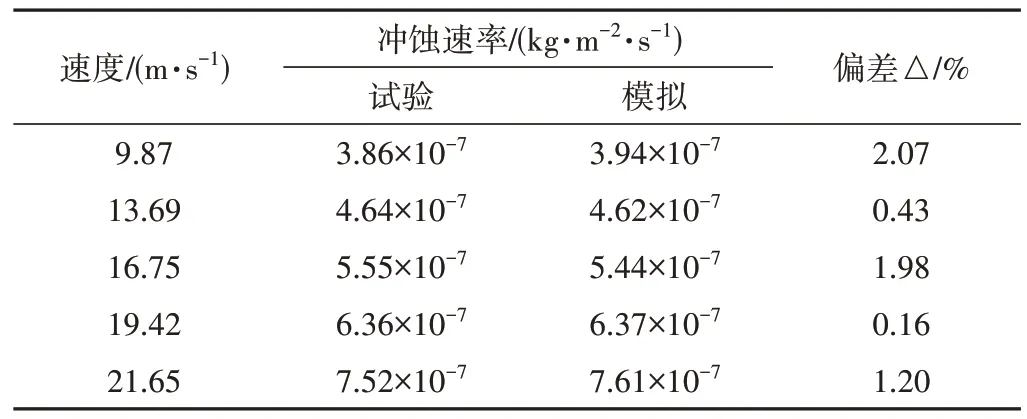
表2 喷头冲蚀速率结果对比Tab.2 Comparison of erosion rate results of sprinkler

2.2 进口流速对锥角高度的影响

在冲蚀过程中，喷盘中心的锥面逐步扩大，锥角高度下降，这是由于固体颗粒跟随流体流动，与锥角壁面直接冲击造成磨损。根据试验结果，不同流速下的锥角高度变化如图6所示，从图6中可以看出，喷盘的锥角高度初始值为2.80 mm，当进口流速从9.87 m/s 增加到21.65 m/s 且冲蚀时间为48 h 时，锥角高度分别下降到2.48 mm、2.39 mm、2.32 mm、2.25 mm和2.23 mm，下降幅度为20.36%。随着冲蚀的进行，喷盘的锥角高度与时间基本呈现出线性关系，而且流速越大，锥角高度下降越快，冲蚀情况越严重。

图6 不同速度下的锥角高度变化Fig.6 Cone angle height changes at different velocities

2.3 进口流速对流道长度的影响

通过冲蚀试验观察到各时段的流道长度和分水台长度不断减小，这是由于流体撞击锥角之后沿着各流道流动，颗粒随其在流道与分水台凸起处发生碰撞，造成切削磨损和冲击磨损。图7 为不同流速下的流道长度随时间的变化图，从图7中可以看出，流道长度随着时间增加逐渐减小，流道长度的减小量随着流速的增大而增加，这是由于冲蚀速率发生变化。喷盘的流道长度初始值为10.50 mm，当冲蚀时间为48 h 且进口流速由9.87 m/s 增加到21.65 m/s 时，流道长度分别减小到8.88 mm、8.30 mm、7.82 mm、7.71 mm 和7.11 mm，减小幅度为32.29%。

图7 不同速度下的流道长度变化Fig.7 Change of runner length at different velocities

2.4 含沙量对喷头结构冲蚀的影响

通过数值模拟能够得到不同含沙量、不同速度下的喷盘冲蚀速率如图8 所示。从图8 中可以看出，喷盘的冲蚀速率随着进口流速的增大而增加，在含沙量为3%时，当进口流速从9.87 m/s 增加到21.65 m/s 时，冲蚀速率从1.18×10-6kg/(m2·s)增大到2.24×10-6kg/(m2·s)，这是由于固体颗粒在速度较大的连续相流体中受到的惯性力较大，加剧了颗粒与壁面的冲击强度，导致冲蚀速率增大；随着含沙量的增加，喷盘的冲蚀速率与进口流速之间呈现出愈发强烈的指数关系，说明含沙量越大，喷盘的冲蚀情况越严重，这是由于含沙量的增大使单位体积内的颗粒数量增加，提高了单位面积上颗粒与壁面发生碰撞的概率，导致冲蚀速率升高。