借助问题链设计，发展“后建构”推理

王琳 薛莺

一、教学目标

对“圆”整个单元知识进行归纳，使学生在活动中形成知识网络，通过练习，提高学生分析问题、解决问题的能力，同时渗透分类讨论、数形结合思想；使学生在课堂活动中，勇于探索图形间的相互关系，培养学生的空间观念，发展学生的合情推理能力。

二、教学重难点

理解圆及其有关概念、性质定理、判定定理；运用相关知识解决实际问题；渗透数形结合、分类讨论思想。

三、教学片段

1.选好切入点

本节课以教材中本章开头引用的“一中同长”为切入点，复习圆的概念。

师：什么是圆？确定一个圆需要几个条件？

生1：圆是到定点的距离等于定长的点的集合。

生2：确定一个圆需要两个条件——圆心和半径。

师：平面内的点和圆有几种位置关系？（由此引出“点与圆的位置关系”。）

生3：有三种位置关系。当点到圆心的距离等于半径，则点在圆上；当点到圆心的距离小于半径，则点在圆内；当点到圆心的距离大于半径，则点在圆外。

探究1：圆内一点P到圆上哪个点距离最小？到哪个点距离最大？

（学生直观感知这两个点都在过点P的直径上。）

探究2：如果点P在圆外呢？

（学生发现这两个点仍旧在此直径上。）

设计意图：选择合适的知识点作为切入点。一是注重基础性，即低起点，课堂刚开始能让更多的学生积极参与；二是注重生长性，即高落点，学生以此知识点为起点，结合已有的基础和经验，在解决问题过程中能够不断生长出其他数学知识。相比新课的教学，复习课不仅要注重知识的巩固，还需关注能力的提升。

2.排好“明暗线”

（1）请学生动手操作探究，尝试画出过圆内一点的最长弦与最短弦。此为“明线”，目的是复习圆的垂径定理及有关圆的一些计算。

师：过圆内的一点P可以画多少条弦？

生（齐）：无数条。

师：这无数条弦中，有最长的吗？有最短的吗？

生（齐）：最长的弦是过点P的一条直径。

学生分小组讨论最短的弦是否存在？若存在，如何画？

学生经讨论发现：最短弦是与过点P的直径垂直的弦。

设计意图：过圆内一点P，画最长弦与最短弦，构建垂径定理的基本图形，然后设计圆这一章的计算类问题。笔者安排了这样一条“明线”，试图让这个知识点生长蔓延，串联起章节中的其他知识点，以便于学生构建完整的知识体系。

（2）请学生细致观察探究，寻找图中相等的角。此为“暗线”，目的是复习圆周角定理及结合相似三角形的知识进行综合应用。

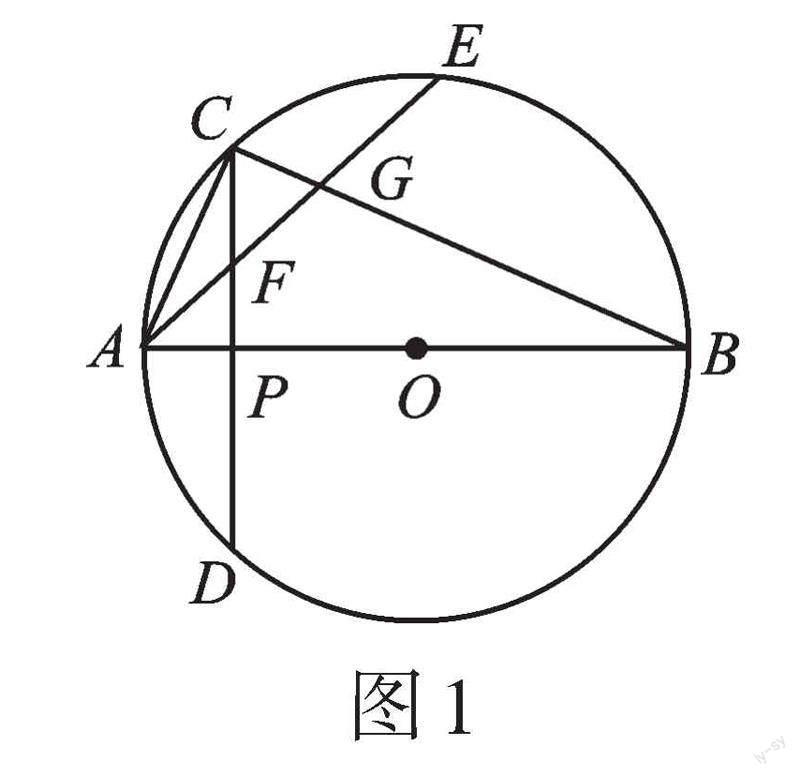
例1 在图1中的[BC]上取一点E，使 [CE]=[AC]，AB⊥CD，连接AE，分别交CD、CB于点F、G。连接AC。

师：由垂径定理，可以得到相等的弧，再结合圆周角定理，由相等的弧可以得到相等的角。此图中你能找出哪些角相等吗？

小组讨论，教师板书，学生得出结论：

[CE]=[AC]=[AD]→∠CAE=∠B=∠ACD；

[CB]=[BD]→∠CAB=∠BCD；

AB为直径→∠ACB=90°=∠APC=∠BPC；

对顶角相等→∠AFP=∠CFG，∠CGF=∠BGE。

師：通过你所找到的相等的角，能试着说明F为AG的中点吗？

生4：可以。因为∠ACD=∠CAE，所以FA=FC；因为∠ACB=90°，所以∠ACD+∠FCG=∠CAE+∠CGF=90°，所以∠FCG=∠FGC，所以FC=FG。又因为FA=FC，所以FA=FG，即F为AG的中点。

师：这位同学结合“等角对等边”“等角的余角相等”的知识，证明了F为AG的中点。

师：若已知AC=6，BC=8，你能计算出图中哪些线段的长？

小组进行讨论，教师板书、总结。

师：通过相似、勾股定理等知识的综合运用，同学们求出了此图中的每条线段的长。

设计意图：由寻找图中相等的角这条“暗线”，围绕知识要点，让学生发散思维。再用知识点编题，设置开放性问题，让学生说缘由，谈解法，在探究的过程中逐步形成知识“明线”。

3.拓展知识面

例2 在平面直角坐标系中，点A与点B的坐标分别是（2，0）、（12，0）。

（1）若点P在y轴上，且∠APB=45°，满足条件的点P有几个？试求出点P的坐标。

（2）若点Q在y轴上移动，当∠AQB最大时，求点Q的坐标。

师：题目难度有点大，同学们能否在平面直角坐标系内先找一个点M，满足∠AMB=45°？

生5：可以作一个以AB为腰的等腰直角三角形ABM，这样就可以构造出一个45°角了。

师：此时的点M并不在y轴上，怎么办？

生6：可以作△ABM的外接圆， [AB]所对的圆周角都能满足45°的条件，所以只要作△ABM的外接圆，优弧[AMB]与y轴的交点即为我们所寻找的点P。

师：满足条件的点P有几个？

生7：优弧[AMB]与y轴有2个交点，所以这样的点P有2个。

生8：不对，由对称性可知，可以在y轴的正负半轴上各找到2个，所以满足条件的点P有4个。

师：该同学考虑问题很全面！请同学们结合数据，课后求一下点P的坐标。同学们利用圆周角的性质，构造圆，来解决“定边对定角”问题，那么，同学们能不能再尝试利用“同弧所对的圆内角、圆周角、圆外角”之间的大小关系，来解决第（2）小题呢？

生：……

设计意图：通过前面的复习铺垫，题目的难度逐步加大，学生无法清楚地表达思路，需要教师给予适当的点拨、启示。最后，以构造圆的问题结束课堂，大大提高了学生的逆向思维能力。圆不仅可以作为题目的背景，也可以成为我们解决其他数学问题的工具。同时（2）又在（1）的基础上增加了角的最值问题，拓展了学生的知识面，提升了学生的思维维度，体现了数学知识之间是处处关联的。

四、教学反思

1. 连点成线，形成知识网络

本节复习课采用2道例题题组，将圆中的相关知识容纳其中，既帮助学生复习了圆中的基本概念和基本技能，又帮助学生理清了分散的知识是如何相互关联的。这种关联的建立有助于学生在解决复杂问题时能够高效且快速地提取到所需要的信息组，并在已有信息的基础上开拓出一些创造性的思路。

2. 设问开放，培养发散思维

例1属于开放题，充分调动了学生已有的知识储备。在由浅入深的解决问题的过程中，在相互讨论的过程中，学生吸取思维碰撞中产生出的思维火花，从而生成对已有知识新的理解，建立知识之间更紧密的联系，使得思维向着更高阶的方向发展。

3. 变式练习，破解思维定式

通过一题多变，即数学上的变式教学来帮助学生理清基本概念。学生对基本知识和技能理解和掌握后，教师再有目的和计划地改变题目的非本质特征，在“以不变应万变”中，提高课堂的教学效率，培养学生思维品质。这里的不变指的是基于教材的基本概念、定理和公式。

（作者单位：1.江苏省无锡市东林中学；2.江苏省无锡市东绛实验学校）

本文系江苏省教育科学“十四五”规划重点课题“指向初中生代数推理能力发展的问题链设计研究”（课题编号：C-b/2021/02/01）；江苏省现代教育技术研究2022年立项课题“信息技术背景下的初中后建构课堂教学策略研究”（课题编号：2022-R-100847）阶段性研究成果。