两跨连续钢-再生混凝土组合梁长期性能研究*

尤广迪 李 峰 张启军 王庆贺 韩 涛

(1.沈阳建筑大学土木工程学院, 沈阳 110168; 2.中建七局交通建设有限公司, 郑州 450004)

钢-混凝土组合梁因其承载能力高、刚度大、施工便捷等优点,广泛应用于高层建筑和大跨度公共结构中[1-4];与此同时,随着我国城镇化的快速发展,建筑业对砂石的需求量不断增大,大量开山采石已严重破坏生态环境[5]。因此,大力发展再生混凝土,是解决我国砂石资源短缺,提高废旧混凝土资源回收利用的重要途径[6]。具体而言,由于钢-混凝土组合梁抗弯刚度大、承载力高,将再生混凝土引入钢-混凝土组合梁可以有效拓宽再生混凝土的工程应用范围[4]。

国内外学者对再生混凝土长期性能进行了系统研究,结果表明,与普通混凝土相比,再生粗骨料取代率为100%的再生混凝土收缩变形增大27.6%～77.0%,徐变变形增大23.0%～120.0%[7-11]。对于钢-再生混凝土组合梁的各项性能,目前学者们研究较少。张建伟等对等配合比的钢-再生混凝土组合梁和钢-普通混凝土组合梁进行了抗弯试验研究[12],发现二者抗弯性能相近且破坏形态相似,与普通混凝土组合梁相比,再生粗骨料取代率为100%时,组合梁抗弯承载力仅降低1.0%、短期刚度降低5.5%。Yang等对单跨钢-再生混凝土组合梁的长期性能进行了研究[13],结果表明,再生粗骨料取代率对其长期性能影响显著,与普通混凝土试件相比,再生粗骨料取代率为100%时,组合梁的长期挠度增加3.5%～17.2%;与采用非均匀收缩徐变模型相比,均匀收缩徐变模型组合梁长期附加挠度增加4.5%～10.3%。

部分学者对单跨钢-普通混凝土组合梁的长期性能进行了试验、有限元和理论分析,研究结果表明,混凝土的收缩徐变对钢-混凝土组合梁长期性能影响显著[14],例如,文献[15-17]通过试验发现,由混凝土收缩徐变引起的组合梁长期挠度为瞬时挠度的1.2～4.0倍;1992年,Wright等提出考虑组合梁收缩应变的曲率计算模型[18];文献[19-22]通过试验、有限元及理论分析,量化了混凝土收缩徐变对钢-混凝土组合梁长期性能的影响,并提出了几种考虑混凝土收缩徐变的组合梁长期性能预测模型;对于两跨连续钢-混凝土组合梁,Gilbert等进行了长期的持荷试验[23],发现组合梁在受340 d收缩徐变的综合作用下,其负弯矩为28 d瞬时载荷的2.01倍;Al-Deen 等对剪切连接度和混凝土徐变对两跨连续组合梁长期性能的影响进行了研究[24],发现当剪切连接度为0.5时,140 d收缩徐变引起的附加挠度是28 d瞬时挠度的40%。

综上,组合梁中混凝土的收缩徐变对其长期性能有较大的影响,而目前学者大都针对单跨组合梁的长期性能进行研究,尚无两跨连续钢-再生混凝土组合梁长期性能研究。基于此,本文采用ABAQUS软件建立两跨连续钢-再生混凝土组合梁长期性能精细化有限元模型,模型可考虑混凝土均匀/非均匀收缩、均匀/非均匀徐变的影响,并基于现有试验验证有限元模型的可靠性;对两跨连续钢-再生混凝土组合梁长期性能进行系统的参数分析,量化各因素对其长期性能的影响,为两跨连续钢-再生混凝土组合梁在工程中的应用提供建议。

1 有限元模型建立

采用ABAQUS软件建立两跨连续钢-混凝土组合梁模型,模型主要包括钢梁、抗剪连接件、钢筋混凝土板或钢-混凝土组合板等部分。为提高计算效率,沿组合梁纵向对称面建立半模型,采用组合楼板的组合梁有限元模型(图1)。

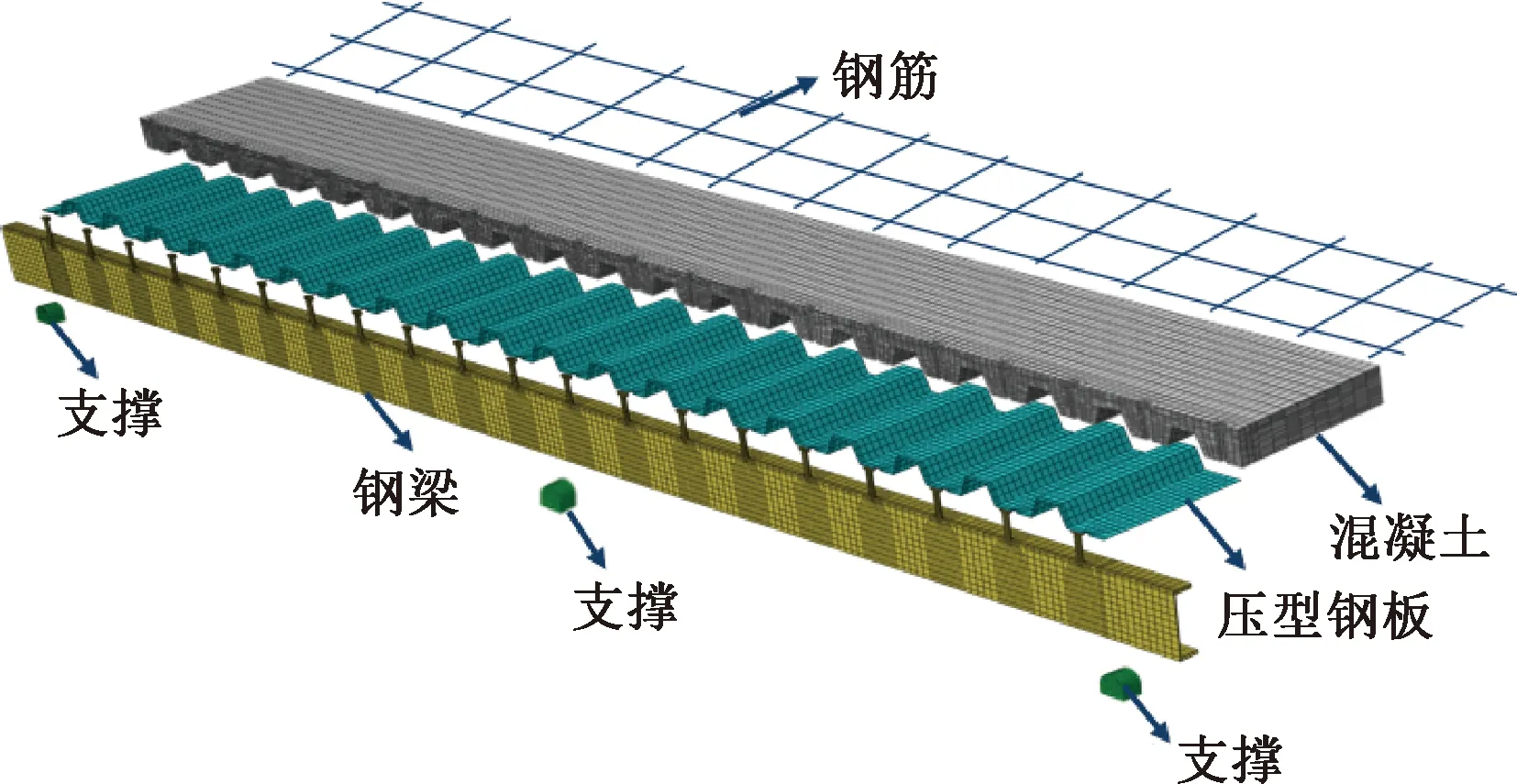
图1 有限元模型示意Fig.1 FEM schemes

1.1 材料力学模型

1.1.1钢 材

在两跨连续钢-再生混凝土组合梁长期性能试验研究中,组合梁中的钢材均未发生破坏[1,23],因此,有限元模型中不考虑钢材的断裂。对于钢梁、栓钉和钢筋的本构关系,采用文献[3]推荐的弹塑性模型,图2a为其应力-应变曲线,在A点处,钢材达到屈服强度fy,弹性阶段OA段的斜率为钢材弹性模量Es;在B点处,钢材开始进入强化阶段,此时的弹性模量为Ep、应变为εp;在C点处,钢材达到极限强度fu,此时的应变为εu。对于压型钢板,在实际工程中,一般由钢板辊压冷弯而成,其极限强度和屈服强度相近,因此本文采用理想弹塑性模型,其应力-应变曲线如图2b所示。

a—钢梁、栓钉、钢筋; b—压型钢板。图2 钢材应力-应变曲线Fig.2 Stress-strain curves for steel materials

1.1.2混凝土

混凝土采用塑性损伤(CDP)模型,泊松比取0.2[4]。普通混凝土的弹性模量Ec,NAC采用欧洲规范EC 2[25]计算,计算公式见式(1):

Ec,NAC=22(fcm/10)0.3

(1)

式中:fcm为混凝土的轴心抗压强度。

对于再生混凝土弹性模量Ec,RAC,采用文献[4]中考虑再生粗骨料取代率(r)与再生粗骨料残余砂浆含量(CRM)的再生混凝土弹性模量(Ec,RAC)模型,即:

(2)

式中:残余砂浆含量(CRM)一般为30%～50%[26],当残余砂浆含量未知时,可采用平均值40%;r为再生粗骨料取代率。

对于再生混凝土与普通混凝土,本文采用Xiao等考虑再生粗骨料取代率(r)影响的混凝土受压应力-应变模型[27],其应力-应变曲线见图3,计算见式(3):

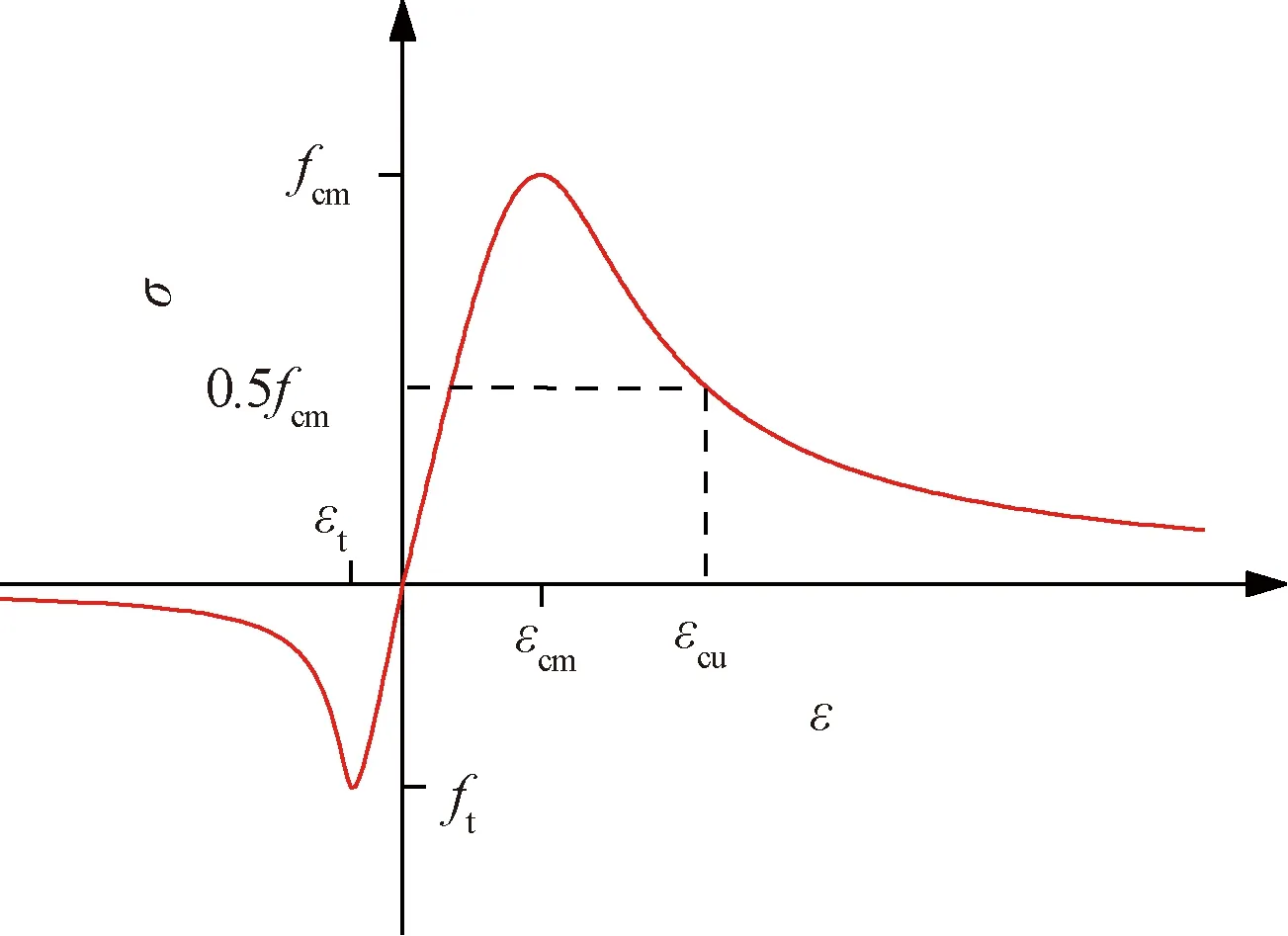
图3 混凝土单轴应力-应变曲线Fig.3 Uniaxial stress-strain curve of concrete

(3)

其中x=εc/εc0

y=σc/fcm

a=2.2(0.748r2-1.231r+0.975)

b=0.8(7.664r+1.142)

式中:σc为混凝土受压应力;εc为混凝土受压应变;εc0为混凝土受压峰值应变;fcm为混凝土抗压强度;a、b为再生粗骨料取代率的影响系数。

再生混凝土与普通混凝土的受拉应力-应变关系相似[28]。对于再生混凝土与普通混凝土,采用Xiao等提出的混凝土受拉应力-应变模型[27],计算见式(4):

y=cx-(c-1)x6

(4)

其中x=εt/εt0

y=σt/ft

c=0.007r+1.19

式中:εt为混凝土受拉应变;εt0为混凝土受拉峰值应变;σt为混凝土的受拉应力;ft为混凝土的抗拉强度;c为参考点处正切模量与余切模量之比。

混凝土的长期变形主要有收缩和徐变两种。混凝土收缩变形εsh(t,z)是由混凝土孔隙率、相对湿度等多种因素所决定的,主要分为干燥收缩和自生收缩。对于带有压型钢板的两跨连续组合梁,由于其组合楼板的单面密闭性,导致在组合楼板厚度方向上相对湿度分布不均匀,因此,其混凝土为非均匀收缩[29],收缩模型见图4a,组合楼板顶面和底面的收缩变形见式(5):

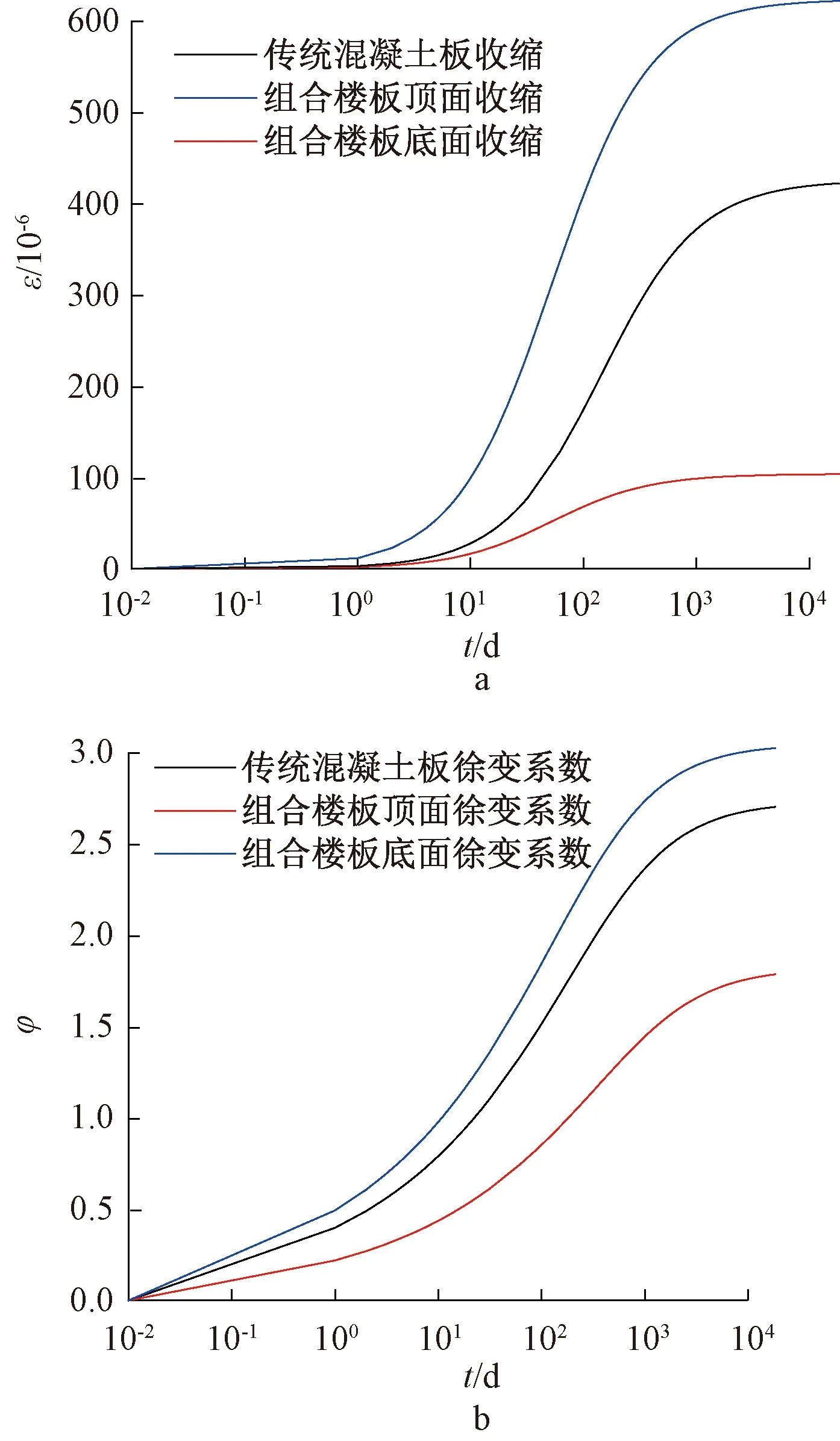
a—收缩变形; b—徐变系数。图4 混凝土长期性能曲线Fig.4 Time-dependent behaviour curve of concrete

εsh,top=(1.6+0.1r)εsh

(5a)

εsh,bot=(1/6-r/4)εsh,top

(5b)

式中:εsh,top为组合梁楼板顶面收缩;εsh,bot为组合梁楼板底面收缩;εsh为混凝土总收缩,即自生收缩εsh,au与干燥收缩εsh,dry之和。

现有的再生混凝土收缩模型是在普通混凝土收缩模型基础上修正得到的。对于普通混凝土,本文采用欧洲规范EC 2[25]中的普通混凝土收缩模型;对于再生混凝土,本文采用笔者前期对普通混凝土收缩模型修正得到的再生混凝土收缩模型[29]。其中,普通混凝土的自生收缩变形随龄期的变化规律见式(6):

(6a)

(6b)

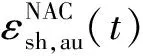
普通混凝土的干燥收缩模型见式(7):

(7)

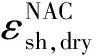
(8)

(9)

式中:κsh,a为残余砂浆对骨料刚度降低的影响系数;κsh,f为基体混凝土抗压强度对再生混凝土干燥收缩性能的影响系数。

对于带有压型钢板的两跨连续组合梁,混凝土的徐变变形εcr(t,t0,z)与收缩变形相似,其徐变模型见图4b。对于普通混凝土,本文采用欧洲规范EC 2[25]中的徐变模型,组合楼板顶面采用环境相对湿度,底面的相对湿度取90%[29],计算见式(10):

φ(t,t0,z)=φ0βc(t,t0)

(10)

式中:φ0为混凝土名义徐变系数;βc(t,t0)为混凝土徐变发展系数;t0为开始计算的时间。

对于再生混凝土,本文采用Geng等考虑残余砂浆KRCA和基体混凝土强度系数可恢复徐变系数KRC综合影响的徐变预测模型[7],计算见式(11):

φRAC(t,t0)=KRCAKRCφNAC(t,t0)

(11)

式中:φRAC、φNAC分别为再生混凝土和普通混凝土的徐变系数。

1.2 单元选择及网格划分

有限元模型中混凝土、钢梁、栓钉采用六面体八结点实体单元(C3D8R),压型钢板采用四结点壳单元(S4R),钢筋采用两结点桁架单元(T3D2)。网格划分时,钢梁腹板与下翼缘最大网格尺寸为20 mm;钢梁上翼缘最大网格尺寸为10 mm;栓钉及栓钉附近的混凝土和压型钢板网格尺寸为4～10 mm,其余部分网格尺寸为20～40 mm;钢筋网格大小为40 mm。

1.3 分析过程

两跨连续钢-再生混凝土组合梁的长期性能模拟主要包括瞬时荷载施加及长期荷载施加两个阶段。

第一阶段:模拟组合梁在瞬时荷载作用下的结构响应,此阶段荷载延续至第二阶段结束。

第二阶段:模拟组合梁在荷载持续作用下,考虑混凝土均匀/非均匀收缩、均匀/非均匀徐变影响的长期性能。通过对混凝土降温模拟混凝土收缩变形;基于龄期调整的有效模量法模拟混凝土的徐变变形。其中,温度场绝对零度为-273 ℃,斯忒藩-玻尔兹曼常数(Stefan-Boltzmann constant)为5.67×10-8,混凝土整体的初始温度为T0(室温),导热系数为1.355 W/(m·K),比热容为1 230.5 J/(kg·K)[4]。混凝土随着温度的降低而收缩,利用混凝土的膨胀系数确定混凝土的温度收缩梯度,本文中混凝土的温度收缩梯度为10-5/℃。对于采用钢-混凝土组合楼板的两跨连续组合梁,通过对混凝土板上下表面设置不同的温度,使温度沿混凝土板厚度方向非均匀分布,以模拟混凝土的非均匀收缩分布,对于采用钢筋混凝土楼板的组合梁,混凝土板上下表面设置相同温度,以模拟混凝土的均匀收缩。

2 有限元模型验证

对现有的两跨连续钢-再生混凝土组合梁长期性能试验进行有限元模拟,具体包括文献[23]中2组采用钢筋混凝土楼板的两跨连续钢-再生混凝土组合梁试件和文献[24]中1组采用钢筋混凝土楼板的两跨连续钢-再生混凝土组合梁试件。组合梁长期试验的主要参数与结果见表1。

表1 两跨连续钢-再生混凝土组合梁长期试验参数与主要结果Table 1 Long-term test behaviour and main results of two-span continuous steel-concrete composite beams

文献[23]对试件B1与B2进行了340 d的长期性能试验,其中,试件B1承受自重荷载1.92 kN/m、试件B2承受自重与均布荷载共6.67 kN/m。图5为B1、B2长期性能试验结果与有限元模拟结果的对比,由图5a可以发现,340 d时,B1跨中长期挠度的试验结果与有限元结果分别为4.95,4.92 mm,二者相差0.6%;由图5b可以发现,340 d时,B2跨中长期挠度的试验结果与有限元结果分别为7.98,7.90 mm,二者相差1.0%;由图5c可以发现,B2中支座负弯矩的试验结果与有限元结果分别为62.7,65.06 kN·m,二者相差3.77%。其中,组合梁长期挠度早期模拟不理想主要是因为,有限元模拟采用的是试验过程的平均相对湿度。

a—试件B1挠度对比; b—试件B2挠度对比; c—试件B2弯矩对比。图5 B1、B2长期性能试验与有限元结果对比Fig.5 Comparison of long-term performance tests and finite element results of B1 and B2

文献[24]对试件CCB1进行了140 d的长期性能试验,其承受自重与均布荷载共8.16 kN/m。图6为CCB1跨中长期挠度的试验结果与有限元模拟结果的对比。可以发现,140 d时,试件长期挠度的试验值与有限元结果分别为18.02,15.92 mm,二者相差11.7%。由以上对比结果可知,本文建立的有限元模型可以较好地预测两跨连续钢-混凝土组合梁的长期性能。

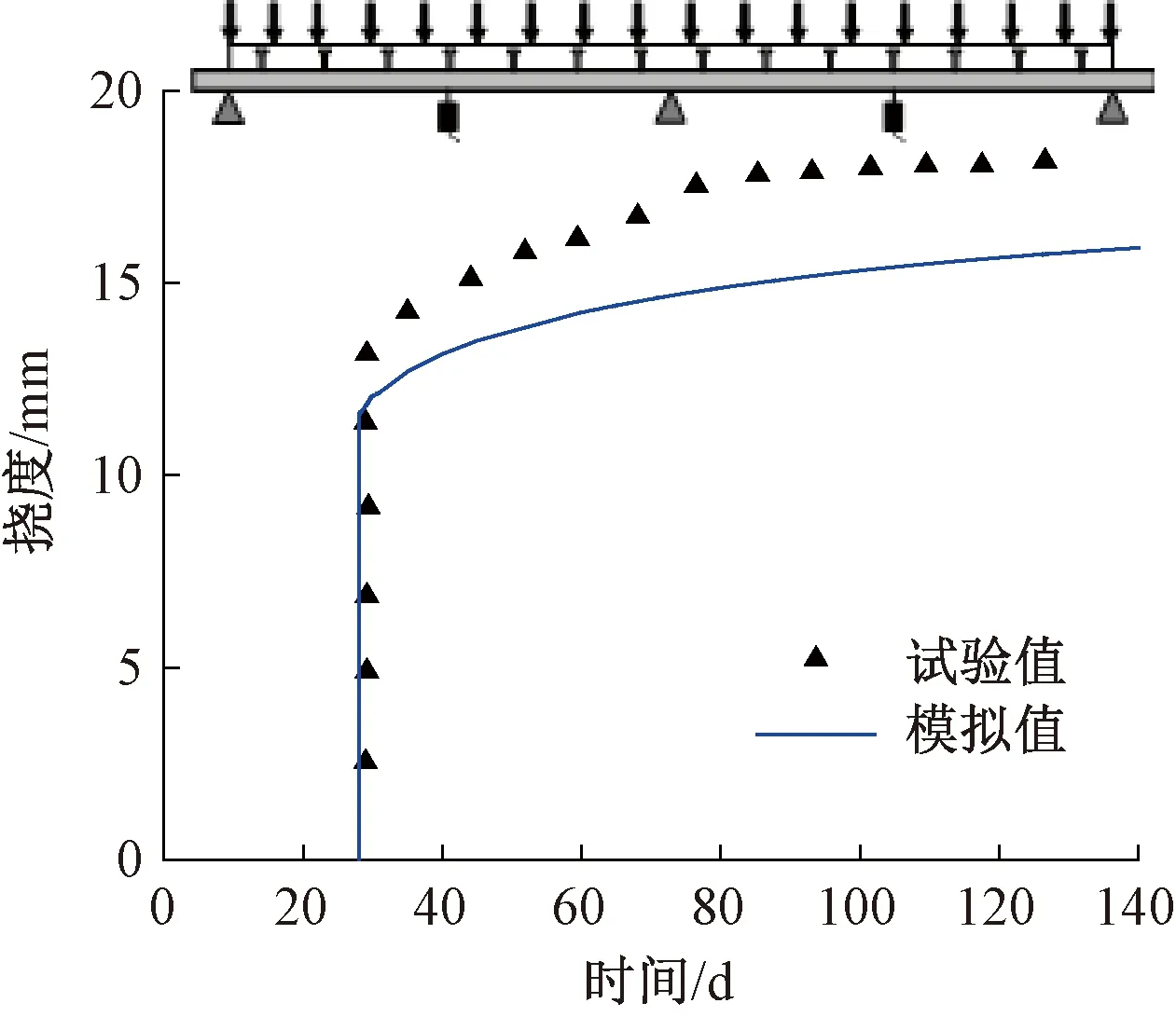
图6 CCB1长期挠度试验与有限元结果对比Fig.6 Comparison of long-term deflection test and FE results of CCB1

3 有限元参数分析

两跨连续钢-再生混凝土组合梁的长期性能受到多因素的影响,例如楼板类型、楼板厚度、环境相对湿度等,本节对两跨连续钢-再生混凝土组合梁的长期性能进行参数分析,量化各因素对两跨连续钢-再生混凝土组合梁长期性能的影响。

3.1 参数范围

有限元参数分析时,组合梁采用C30混凝土和Q345钢材,纵向受压钢筋与横向分布钢筋均为φ12@200,长期均布荷载为恒荷载与活荷载的准永久组合,标准养护28 d后,组合梁承担长期荷载作用,持荷时间为50 a。参数主要包括再生粗骨料取代率(r)、楼板类型(开口型组合板、闭口型组合板和钢筋混凝土板)、楼板厚度(h)和环境相对湿度(RH),具体参数及取值范围见表2。

表2 有限元分析主要参数及取值范围Table 2 FE Parameters and their scopes

3.2 再生粗骨料的影响

图7分析了再生粗骨料取代率对两跨连续钢-再生混凝土组合梁长期挠度的影响。结果表明,组合梁长期挠度随再生粗骨料取代率的增加而增加。具体而言,对于采用开口型组合楼板的两跨连续组合梁,与普通混凝土试件相比,再生粗骨料取代率为50%和100%时,组合梁长期挠度分别增加6.23%和14.84%;对于采用闭口型组合楼板的两跨连续组合梁,与普通混凝土试件相比,再生粗骨料取代率为50%和100%时,组合梁长期挠度分别增加6.47%和13.57%;对于采用钢筋混凝土楼板的两跨连续组合梁,与普通混凝土试件相比,再生粗骨料取代率为50%和100%时,组合梁长期挠度分别增加9.62%和19.63%。同时,在综合考虑楼板厚度与环境相对湿度的影响后,两跨连续钢-再生混凝土组合梁长期挠度的变化范围将进一步增大,具体为,与普通混凝土试件相比,再生粗骨料取代率为50%和100%时,两跨连续钢-再生混凝土组合梁长期挠度分别增加5.52%～9.72%和12.98%～20.39%。分析其原因是,由于再生粗骨料附着残余砂浆,导致在长期荷载作用下再生混凝土的收缩徐变明显大于普通混凝土,且随着再生粗骨料取代率的增大而增大,因此使得两跨连续钢-再生混凝土组合梁的长期挠度随再生粗骨料取代率的增加而增大。

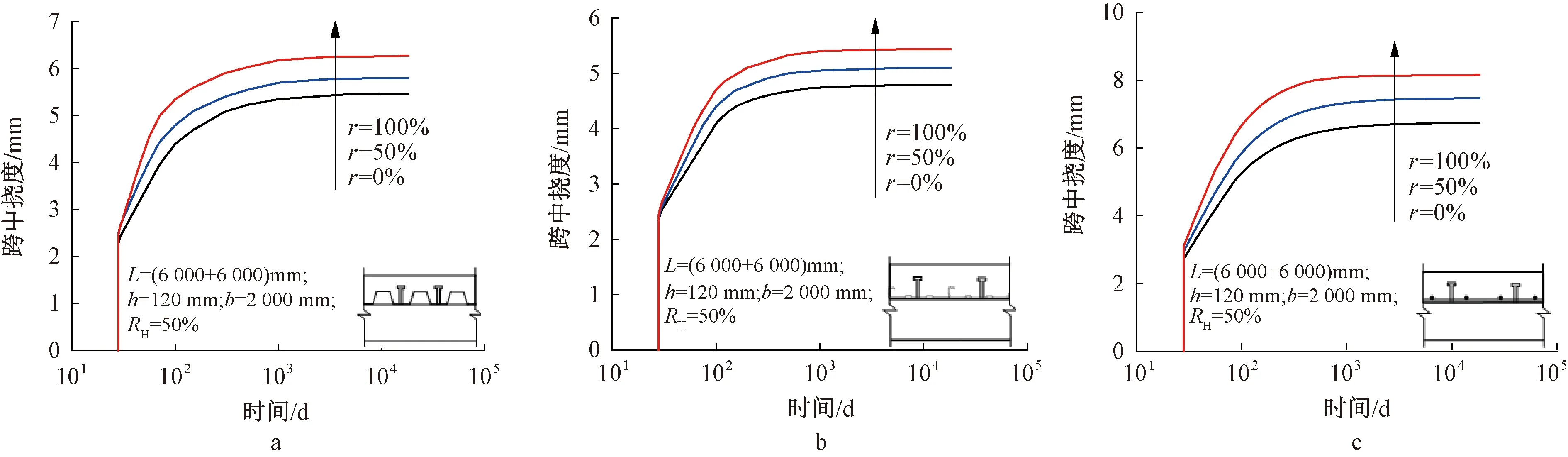
a—采用开口型组合楼板的组合梁; b—采用闭口型组合楼板的组合梁; c—采用钢筋混凝土楼板的组合梁。图7 再生粗骨料取代率对组合梁长期挠度的影响Fig.7 Influence of the replacement rate of recycled coarse aggregate on the long-term deflection of composite beams

3.3 楼板类型的影响

图8分析了楼板类型对两跨连续钢-再生混凝土组合梁长期挠度与瞬时挠度比值的影响。结果表明,在相同再生粗骨料取代率下,采用开口型和闭口型组合楼板的组合梁长期挠度与瞬时挠度比值小于采用钢筋混凝土楼板的组合梁长期挠度与瞬时挠度比值。具体而言,再生粗骨料取代率为0%时,与钢筋混凝土楼板组合梁相比,开口型和闭口型组合楼板组合梁的长期挠度与瞬时挠度比值分别减少8.04%和18.49%;再生粗骨料取代率为100%时,与钢筋混凝土楼板组合梁相比,开口型和闭口型组合楼板组合梁的长期挠度与瞬时挠度比值分别减少12.08%和19.56%。其原因是,对于采用开口型和闭口型组合楼板的组合梁,由于其楼板底部具有密闭性,导致混凝土沿组合楼板的截面高度方向非均匀收缩;对于采用钢筋混凝土楼板的组合梁,钢筋混凝土楼板上下表面的混凝土均与外界直接接触,沿楼板高度方向为均匀收缩。与均匀收缩相比,非均匀收缩的混凝土楼板收缩作用较小,导致其组合梁长期附加挠度较小。因此,采用开口型和闭口型组合楼板的两跨连续钢-再生混凝土组合梁长期挠度与瞬时挠度比值小于采用钢筋混凝土楼板的两跨连续钢-再生混凝土组合梁。

图8 楼板类型对组合梁长期挠度与瞬时挠度比值的影响Fig.8 Influence of floor type on ratio of long-term deflection to instantaneous deflection of composite beams

3.4 楼板厚度的影响

图9分析了楼板厚度对两跨连续钢-再生混凝土组合梁长期挠度的影响。结果表明,在相同再生粗骨料取代率下,组合梁长期挠度随楼板厚度的增加而减小。以采用再生粗骨料取代率为100%的钢筋混凝土板组合梁为例,与楼板厚度为120 mm的组合梁相比,楼板厚度为135,150 mm时,组合梁的长期挠度分别减少5.68%和11.93%。其原因是,随着楼板厚度的增加,组合梁抗弯刚度增大且混凝土收缩徐变减小,因此,两跨连续钢-再生混凝土组合梁的长期挠度随楼板厚度的增大而减小。

a—采用钢筋混凝土楼板的组合梁; b—采用闭口型组合楼板的组合梁。图9 楼板厚度对组合梁长期挠度的影响Fig.9 Influence of floor thickness on long-term deflection of composite beams

3.5 环境相对湿度的影响

图10分析了环境相对湿度对两跨连续钢-再生混凝土组合梁长期挠度的影响。结果表明:在相同再生粗骨料取代率下,组合梁长期挠度随相对湿度的增加而减小;对于采用闭口型组合楼板的两跨连续组合梁,当再生粗骨料取代率为0%时,与相对湿度为30%的组合梁相比,相对湿度为50%和70%的组合梁的长期挠度分别减少2.84%和9.74%;再生粗骨料取代率为50%时,与相对湿度为30%的组合梁相比,相对湿度为50%和70%的组合梁的长期挠度分别减少2.86%和9.52%;再生粗骨料取代率为100%时,与相对湿度为30%的组合梁相比,相对湿度为50%和70%的组合梁的长期挠度分别减少2.33%和9.34%。分析原因可知,随着环境相对湿度的增加,混凝土的收缩和徐变变形均减小,因此,两跨连续钢-再生混凝土组合梁的长期挠度随环境相对湿度的增加而减小。

a—采用钢筋混凝土楼板的组合梁; b—采用闭口型组合楼板的组合梁。图10 环境相对湿度对组合梁长期挠度的影响Fig.10 Influence of ambient relative humidity on long-term deflection of composite beams

4 结 论

1)基于ABAQUS软件建立两跨连续钢-再生混凝土组合梁长期性能有限元模型,模型可考虑混凝土(非)均匀收缩、(非)均匀徐变的影响;对现有的两跨连续钢-再生混凝土组合梁长期性能试验进行有限元模拟,发现长期挠度的有限元模拟结果与试验结果比值的平均值和标准差分别为0.956和0.017。

2)两跨连续钢-再生混凝土组合梁的长期挠度随再生粗骨料取代率的增加而增大。与普通混凝土试件相比,再生粗骨料取代率为50%和100%时,两跨连续钢-再生混凝土组合梁长期挠度分别增加5.52%～9.72%和12.98%～20.39%。

3)采用开口型和闭口型组合楼板的组合梁长期挠度与瞬时挠度的比值小于采用钢筋混凝土楼板的组合梁。与采用钢筋混凝土楼板(均匀收缩徐变模型)的组合梁相比,采用开口型和闭口型组合楼板的组合梁(非均匀收缩徐变)长期挠度与瞬时挠度的比值减少8.04%～19.56%,故应针对不同的楼板类型选用不同的收缩徐变模型。