基于事件触发机制的多飞行器有限时间协同制导方法

2023-07-24李俊贤闫华杰范军芳

宇航学报 2023年6期

纪毅，李俊贤，2，王伟，闫华杰，2，范军芳，2

(1. 北京信息科技大学自动化学院，北京 100192；2. 高动态导航技术北京市重点实验室，北京 100192；3. 北京理工大学宇航学院，北京 100081；4. 无人机自主控制技术北京市重点实验室，北京 100081)

0 引言

具有“打击面大、瞬时毁伤强、冗余高”等优势的多飞行器协同制导方法可有效应对实战中单一飞行器“突防难、毁伤小、容错低”的缺陷,是当前的研究热点。一些传统的研究通过分别对各个飞行器设计时间约束制导律的方法,达到“目标齐射”的效果。文献[1]针对导弹自身速度时变条件下的拦截问题,基于偏置比例导引和平均速度法设计了飞行时间约束制导律。文献[2]基于终端滑模理论,设计了一种无奇点的飞行时间约束制导律。文献[3]针对导弹在大范围机动运动中可能出现的视场丢失问题,将导引头视场角为附加反馈项,实现了对攻击时间及导引头视场角的同时约束。然而,以上飞行时间约束制导律均需在飞行过程中实时精准地估计剩余飞行时间,亦需要据此设计期望终端命中时刻。在实际应用中,期望终端命中时刻须在发射前装订于各飞行器之中,故只能通过计算机仿真得出近似最优值。此外,由于在时间约束制导机制下各个飞行器间不存在信息交流,各自不同的外部干扰对其时间约束性能带来严峻挑战。

时间约束制导机制的固有缺陷可通过研发具有实时通讯功能的多飞行器系统解决。当前的研究主要基于图论与一致性原理,设计集中式或分布式多飞行器协同制导方法[4]。该方法主要可分为两类:一种是引入协调变量并设计控制量,使得各飞行器的剩余时间达到一致[5];另一种是通过建立飞行器间的通信拓扑关系,结合多智能体一致性理论来解决多飞行器间状态不一致的问题[6-7]。文献[8]基于扩张观测器和有限时间收敛控制理论,设计了一种适用于通信拓扑切换情况下的多飞行器一致性协同拦截方法。文献[9]基于多智能体一致性算法和积分滑模理论,设计了一种三维时间角度约束制导律。文献[10]研究了有向拓扑下的多导弹协同制导问题,提出了一种无需径向速度测量的有限时间协同制导律。文献[11]针对多高超声速滑翔飞行器协同制导的问题,提出了一种两阶段一致性制导方法,在实现快速协同轨迹规划的同时控制飞行时间和终端角度。然而,在上述一致性协同制导过程中,各飞行器需实时进行通信交流。在各自运动状态不发生较大变动时,近似一致的信息将加重信道负荷,可能导致承载有效制导指令与运动状态的信息传递受阻,进而影响一致性协同效果。

作为减少控制频次和通信负载的有效途径,事件触发控制机制受到了广泛的关注[12-13]。文献[14-15]针对有向拓扑下的多智能体输出共识问题,提出了基于事件触发的控制协议,避免了智能体间持续不断地低效信息交换。文献[16]基于事件触发函数和牵引控制设计了分布式控制器,适用于具有合作-竞争关系的异构多智能体的一致性问题。文献[17]考虑二阶多智能体系统中各成员速度信息不可测和控制输入有界的情况,通过引入辅助函数设计了一种基于事件触发的一致性协议。文献[18]针对具有事件触发通信的不确定非线性系统的分布式一致性控制问题,提出了一种完全分布式自适应控制方案,并解决了执行机构失效问题。文献[19]针对离散型多智能体系统状态一致性问题,设计了一种基于事件触发预测方案的控制方法,有效降低了控制与通信次数。将事件触发机制引入多飞行器协同制导方法,具有以下优势:1) 制导控制指令并非连续生成,给执行机构留出足够的执行时间,适用于时间滞后系统;2) 执行机构仅执行有限次数的指令,可在达到协同制导目的同时,有效降低能量损失,理论上可提升射程;3) 复杂的战场电磁环境难以保证通信系统长时间有效工作,此时,主动降低通讯需求可提升协同制导的可靠性。

此外,多飞行器协同制导系统各成员需在制导段调整状态至趋同,并精准命中目标。通常,这一过程时间较短(通常不足1 min),有必要设计有限时间一致性方法。

为规避时间约束制导机制的固有缺陷,降低多飞行器间的通讯需求,提升协同制导的可靠性,在有限时间内实现多飞行器的一致性,本文面向多飞行器高精度协同制导问题,设计了两阶段制导律,提出具有有限时间收敛功能的终端滑模面,构建事件触发机制下的有限时间一致性协议,主要贡献与创新点如下:1) 传统研究工作多基于二阶多智能体动力学系统设计协同制导方法。本文通过引入中间变量和设计非奇异终端滑模面,将多飞行器协同制导动力学模型表述为一阶多智能体系统,简化了设计过程。2) 传统研究工作多采用均值一致性方法,为考虑有限时间收敛的需求。本文考虑实际执行过程中的不同沟通方式,分别设计了集中式与分布式多飞行器有限时间一致性制导方法。3) 设计了基于事件触发机制的多飞行器系统一致性制导方法。与传统一致性协同方法相比,该方法在保证多飞行器运动状态快速一致性收敛的同时,通过事件触发机制降低了控制频次和通信负载,提升了多飞行器系统的通信效率与可靠性。

1 多飞行器协同制导问题描述

首先阐述代数图论与引理,其次建立了多飞行器系制导动力学模型,提出了两阶段制导方法,最后将协同制导问题转化为带有滑模面的一阶多智能体系统一致性问题。

1.1 代数图论与引理

(1)

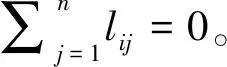
引理2[21].假设V(x)为定义于U⊂n上的C1型光滑正定函数。对于任意β1>0,β2∈(0,1),β3>0,存在定义于U⊂n的函数满足,有函数不等式成立。此时存在数域U0⊂n满足任意从其出发的V(x)均可在有限时间Treach内到达V(x)=0的状态,且Treach≤ln(β3V1-β2(x0)+β1/β1)/β3(1-β2)。

1.2 多飞行器系统制导动力学模型

飞行器制导三维几何场景如图1所示。惯性坐标系定义为O-XYZ,O为坐标原点;M与T分别代表飞行器和静止目标,R为飞行器与目标的相对距离,VM为飞行器速度,本文视为一常数,且各飞行器速度相等;OA为飞行器速度方向,OB为飞行器纵轴方向,OC为视线方向,平面OAB垂直于平面OBC;θM为飞行器纵轴与飞行器速度的夹角,φM为视线与飞行器纵轴的夹角,θM与φM的方向互相垂直;θL与φL分别为弹目视线角在惯性系下的垂直分量与水平分量;σ为视线与飞行器速度方向夹角。将飞行器速度看作常值,弹目相对运动关系可由如下微分方程表示[21]：

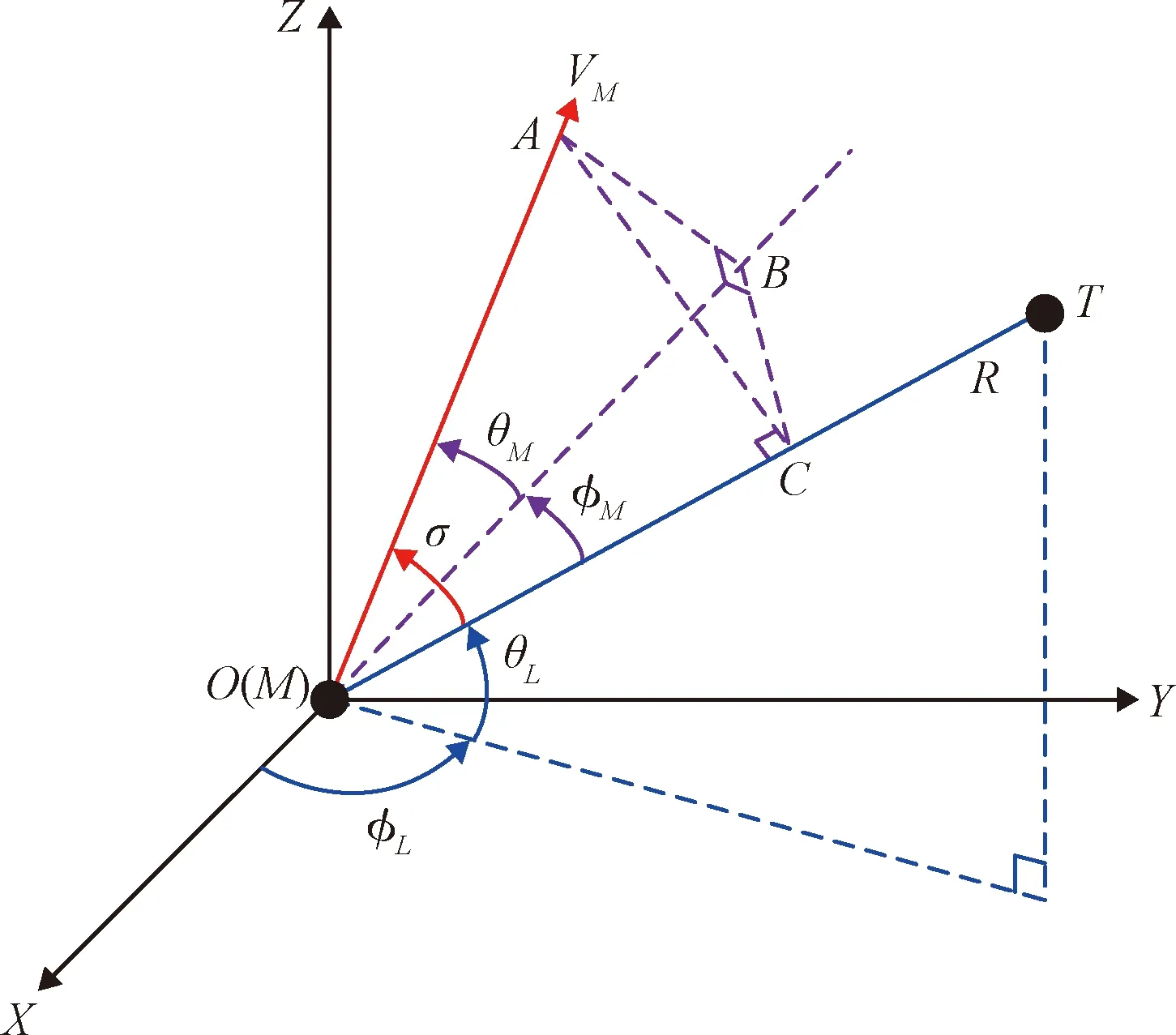
图1 制导几何关系图

(2)

式中:az和ay分别表示飞行器俯仰和偏航加速度。

由图1可得σ的计算公式为

σ=arccos(cosθMcosφM)

(3)

求式(3)的一阶时间导数,并将式(2)代入得

(4)

为规避对剩余飞行时间的实时精准估计,定义两个辅助变量

(5)

求式(5)的一阶时间导数,并将式(2)～(4)代入,得

(6)

俯仰、偏航通道方向的控制量可写作

(7)

式中:u为待设计的一致性控制协议。

将式(7)代入式(6),并考虑该成员在由n个个体组成的多飞行器系统内的标号,可得

(8)

对于以上多飞行器系统,其协同任务为:在某一终端时刻控制多个飞行器同时精确命中目标,并保证各飞行器状态趋同。

1.3 两阶段制导方法

为完成多飞行器系统协同制导任务,本节设计两阶段制导方法。在第一阶段通过基于有限时间一致性原理的制导方法,使式(8)中的两个中间变量的一致性误差收敛至零附近的一个小邻域内,即

(9)

式中:εη>0和εj>0皆为微小常数。

第一阶段仅实现了多飞行器系统内各成员状态趋同,并未实现制导。故第二阶段引入三维比例导引制导律(10),以使各飞行器精确命中目标。

(10)

式中:λy和λz为弹目视线角分量,其一阶时间导数可按式(11)求解

(11)

引理 3.[21]若多飞行器系统中各成员具有相同的导航比N,并且具有相同的初始弹目距离R(0),与初始夹角σ(0),那么这些成员的轨迹形状相同。

引理3说明,各飞行器在第一阶段在实现一致性后,各飞行器的轨迹形状相同,在相同的速度下,必将在相同的时间命中目标。

第一阶段仅约束了各飞行器的飞行时间和弹目视线角的数值,并未对交接点位置,弹目时间角方向、速度方向进行约束。因此,各飞行器的交界点位置,飞行方向并不相同。而引理3又进一步证明在实现一致性后,各飞行器的轨迹形状相同。因此,二阶段制导方法具有天然的避碰性,只在考虑各飞行器的体积时,系统内各飞行器会在命中目标前的微小时间段发生碰撞。

1.4 问题描述

选取状态变量x1=η,x2=ζ,则智能体i的动力学模型结合公式(8)可写为

(12)

式中:xi(t)=[xi,1(t),xi,2(t)]T∈2是智能体i的状态向量;ui(t)∈是智能体i的控制量。多智能体系统的网络拓扑可表述为G={V,E,}。

假设 1.多智能体系统的网络通信拓扑形式为无向连通图。

(13)

式中:k>0, 1

上述滑模面的收敛性质可由引理4描述。

对式(13)求一阶时间导数,得

fi(t)+ui(t),i=1,2,…,n

(14)

制导动力学模型(2)、二阶一致性系统模型(8)、(12)与一阶一致性系统模型(14)的转换关系如图2所示。引理4说明,通过控制滑模面(13),即可实现对系统(8)的二阶一致性,进而实现多飞行器制导动力学一致性。

图2 动力学模型转换关系

假设 2.多智能体系统(12)符合Lipschitz条件,即存在一个正常数γ使得

|f(si(t),t)-f(sj(t),t)|≤γ|si(t)-sj(t)|

(15)

2 集中式事件触发一致性制导律

首先对基于事件触发的一致性制导律进行设计,其次通过构造李亚普诺夫方程对多智能体系统的一致性进行分析,最后通过证明相邻两触发点之间存在严格的正下界排除了Zeno现象。

2.1 制导律设计

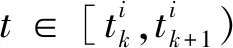
(16)

接下来,设计如下一致性协同方法

u(t)=-ћ1y(t)-ћ1yη1(t)

(17)

式中:ћ1>0, 0<η1<1为待设计参数。

将式(17)代入式(8),即可得到基于事件触发机制的集中式一致性协同制导律。

2.2 一致性分析

采用如式(17)所示的基于事件触发机制的平均一致性协同方法,多智能体系统(12)的一致性性能可用如下定理描述。

定理1.考虑同时满足假设1、2的二阶非线性多智能体系统(12),当γ≤ћ1λ2(L)时,采用基于事件触发机制的集中式有限时间一致性协同方法(17)可使其状态达到一致。

证明：定义二阶多智能体系统(12)滑模面向量为s(t)=[s1(t),…,sn(t)]T,i=1,2,…,n,考虑以下李雅普诺夫函数

(18)

由引理1可知,拉普拉斯矩阵L为半正定矩阵,但当且仅当其特征向量为1时,L对应的特征值为0,此时多智能体系统(12)达成一致性,即si(t)=sj(t),i,j=1,…,n。故V1可用于评价系统(12)的一致性性能。

求(18)式的一阶时间导数,得

u(t))=-yT(t)(ћ1e(t)+ћ1y(t)+ћ1yη1(t)-f(t))

(19)

由假设2可得

(fi(t)-fj(t))-ћ1(1-1)·

(20)

进一步整理得

(21)

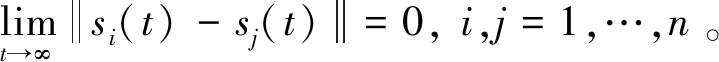
2.3 Zeno现象规避性分析

Zeno现象指在事件触发控制中在有限时间内发生无限次触发,即tk+1-tk<0。采用本章所述的集中式事件触发一致性多智能体系统的Zeno现象规避性可总结为以下定理。

证明：定义(t)=e(t)/y(t),求其一阶时间导数得

(ћ1η1(λN(L)V1(0))(η1-1)/2+ћ1+

(22)

进一步整理得

D+|(t)|≤(ћ1η1(λn(L)V1(0))(η1-1)/2+ћ1+

(ћ1η1(λn(L)V1(0))(η1-1)/2+ћ1+(t))·

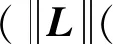
γ+(t))2=(K+(t))2

(23)

3 分布式事件触发一致性制导律

本节面向多智能体系统(12)设计分布式事件触发有限时间一致性制导律,设计流程与上一章相似。

3.1 制导律设计

定义分布式一致性误差为

(24)

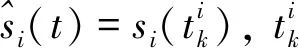
i=1,2,…,n

(25)

分布式事件触发机制如式(26)所示。

(26)

设计如下一致性协同方法

(27)

其中,ћ2>0, 0<η2<1为待设计参数。

将式(27)代入式(8),即可得到基于事件触发机制的分布式一致性协同制导律。

3.2 稳定性分析

采用如式(27)所示的基于事件触发机制的平均一致性协同方法,多智能体系统(12)的一致性性能可用如下定理描述。

定理3.考虑满足假设1、2的二阶非线性多智能体系统(12),当γ≤ћ2λ2(L)时,采用分布式事件触发机制的一致性协同方法(27)可使其状态达到一致。

证明：考虑以下李雅普诺夫函数

(28)

求(28)式的一阶时间导数,得

(fi(t)-fj(t))-ћ2(1-2)·

(29)

根据假设2,有

(30)

3.3 Zeno现象规避性分析

采用本章所述方法的分布式事件触发一致性多智能体系统的Zeno现象规避性可总结为以下定理。

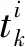
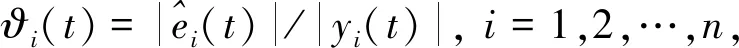
(Ki+ϑi(t))2

(31)

4 仿真校验与结果分析

4.1 仿真设置

通过数值模拟证明了所提出的基于事件触发的协同制导律的有效性,令5枚飞行器以相同的速度Vm=300 m/s攻击静止目标,飞行器加速度上限为amax=60 m/s2,比例导引段的导航比为N=5。飞行器间的通信拓扑关系如图3所示,各飞行器的初始条件如表1所示,一致性制导算法中各参数如表2所示。

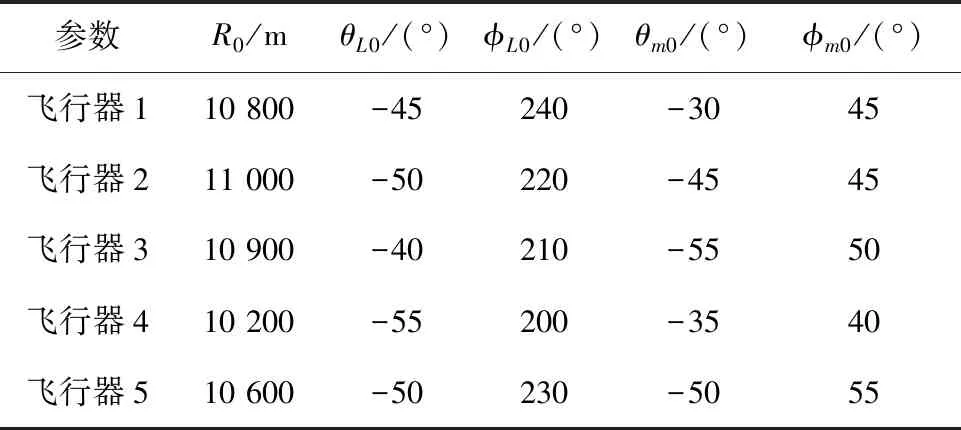
表1 仿真初始条件

表2 仿真参数

图3 多飞行器通信拓扑关系

图3所示多飞行器通信拓扑关系的邻接矩阵和拉普拉斯矩阵为

(32)

4.2 集中式与分布式事件触发制导仿真结果分析

集中式事件触发有限时间一致性制导仿真实验结果如图4所示。图4(a)为各飞行器的纵向、横向加速度曲线。由图4(a)可知,在该一致性制导方法的控制下,多飞行器系统中各成员均在约49.35 s时命中目标。图4(b)形象地描述了两阶段制导方法的特点,各飞行器在24.23收敛至-0.537 4附近一微小邻域,之后切换为比例导引制导律,直到命中目标。图4(c)为各飞行器的事件触发时刻。由上述仿真结果可以看出,在集中式事件触发机制的作用下,各飞行器加速度指令在同一时刻触发。

图4 集中式事件触发一致性制导仿真实验结果

分布式事件触发有限时间一致性制导仿真实验结果如图5所示。由上述仿真结果可知,在该一致性制导方法的控制下,多飞行器系统中各个成员均在约46.18 s时命中目标。各飞行器在20.32 s收敛至-0.546 9附近一微小邻域,之后切换为比例导引制导律,直到命中目标。与集中式事件触发机制不同,在分布式事件触发机制控制下,制导指令由不同飞行器在不同时刻触发,触发时刻如图5(c)所示。

图5 分布式事件触发一致性制导仿真实验结果

值得注意的是,仿真结果出现了初始阶段饱和、抖振等现象,这是由滑模控制方法的固有特性引起的。初始阶段系统轨迹偏离程度大,所需控制量大,故引起控制饱和现象。当系统状态轨迹进入滑模面的另一侧时,又会有相反方向的控制量,故出现抖振现象。但上述现象对系统可靠性的影响较低。由仿真结果可以看出,初始段过载加速度虽有饱和,但其界限为6g,此时飞行器处于满舵状态,持续时间仅约1 s。集中式多飞行器系统的执行机构在10～25 s出现小幅抖振,但在事件触发机制的调节下,保持了较低的频率(5～10 Hz)。在分布式多飞行器系统中,由于事件触发次数较低,抖振现象并未出现。

以上仿真结果说明,在本文提出的两种事件触发有限时间一致性协同制导方法控制下,多飞行器系统中各成员可在同一时刻完成制导任务。

4.3 与经典均值一致性制导方法的对比分析

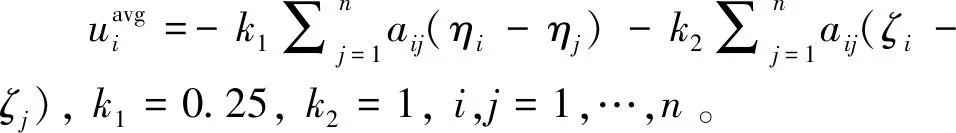
均值一致性协同制导仿真结果如图6所示,图6(a)(b)分别纵向过载与横向过载、中间变量ζ。将以上仿真结果分别与图4、图5中对应部分进行对比,可以看出,各图曲线趋势相似,但图6(a)中过载曲线平滑,不呈现阶跃状。这是因为在均值一致性协同制导过程中,制导指令连续产生,弹载计算机、通信系统、执行机构等组件须连续工作。而在基于事件触发机制的协同制导过程中,上述元器件仅在图4(c)、图5(c)所示的触发点工作即可,在减少控制次数、降低信道负载的同时,亦能保证良好的协同制导效果。