一种卫星姿轨一体化模型预测容错控制方法
2023-07-24孙楚琦孙兆伟
孙楚琦,肖 岩,叶 东,孙兆伟
(哈尔滨工业大学航天学院卫星技术研究所,哈尔滨 150080)
0 引 言
随着航天技术不断革新,大部分卫星在研制过程中加入了标准化外部插件接口的设计,以适应未来计划内或计划外的在轨升级、维护和抢救等空间任务。诸多在轨服务任务的实现都需要进行六自由度机动,用于对接或抵近目标卫星,并调整至满足任务需求的姿态[1-2]。近年来,关于此类六自由度姿轨一体化建模与控制的研究一直是航天领域的研究热点。对于六自由度相对运动建模,考虑卫星轨道运动和姿态运动间有着强耦合,传统方法将轨道运动和姿态运动分开处理的方式难以妥善处理两者之间的耦合关系[3-5]。此外,考虑在轨卫星长期处于空间恶劣环境,卫星上的执行机构因老化或其它不可抗力所导致的效能下降将大大降低卫星机动能力[6-7]。综合上述问题,针对卫星的姿轨一体化容错控制策略具有一定的工程实践意义,并能够为在轨服务的完成提供技术保障。
针对航天器轨道和姿态运动一体化的建模方法现阶段主要分为三种。1)首先是姿轨独立建模方法,其思想为将描述轨道运动和姿态运动的动力学模型联立,形成姿轨一体化动力学模型[8-11]。上述研究中虽然实现了轨道和姿态运动的一体化描述,但是仍然需要通过轨道和姿态之间的耦合关系往复运算,并没有从姿轨耦合特性的本质上进行动力学建模。2)第二种是基于Lie群SE(3)的姿轨一体化建模方法。通过由旋转矩阵与位置矢量构成的三维欧几里得空间里的Lie群,一体化描述刚体在三维空间中的平动和转动。文献[12]借助李群SE(3)指数坐标模型设计了一种鲁棒自适应控制方法。文献[13]研究了SE(3)模型下的考虑执行机构延迟和饱和下的无人机位姿稳定控制方法。文献[14]研究了基于李代数SE(3)和一致扩展卡尔曼滤波的刚体运动一致估计。这种数学工具的缺点是建模中包含较为复杂的矩阵运算,加大了控制器设计的复杂度。3)第三种是基于螺旋位移理论的对偶四元数描述,将四元数和对偶数结合形成一个统一框架的矢量,用于一体化描述平动和转动。文献[15-18]研究了对偶四元数应用于机器人和卫星的六自由度运动建模的状态控制和估计。针对非合作滚转目标,文献[19]设计了一种柔性航天器交会的自适应迭代学习控制。文献[20]建立了基于对偶四元数的电磁配置卫星模型,用于衍射成像任务。李群SE(3)是对偶四元数的齐次变换形式,但是基于对偶四元数的姿轨动力学模型能够给出更简洁的状态空间形式,从而降低控制器设计难度。
航天器姿轨一体化控制通常选取自适应控制、反步法控制、变结构控制等方法进行设计[21]。由于姿轨一体模型具备强耦合、强非线性的特点,相应的控制方法复杂程度高、设计难度大。模型预测控制(Model predictive control,MPC)作为一种能够同时处理约束满足、优化指标、鲁棒性及模型适应性的先进控制综合技术,已经逐步在航天领域中得到应用。当今MPC在航天领域的应用主要体现在航天器交会机动控制和姿态控制中,在基于姿轨耦合动力学模型的位姿控制研究中较少。文献[22]针对六自由度的近距离机动过程,设计了基于序列凸优化的滚动时域制导与控制策略。文献[23]以火星登陆为背景,设计了在若干火星着陆的关键约束条件下的模型预测控制方法。
一般来说,航天器设计采用冗余配置的硬件设施提高系统的可靠性,但是这种措施只能在一定程度上以空间体积为代价换取系统可靠性。为进一步提高系统的可靠性和适用性,在对系统进行控制器设计时考虑系统潜在故障,使控制器具备一定容错能力十分必要。本文研究的主要动机在于试图将MPC与容错控制相结合,设计一种针对航天器姿轨一体控制系统的模型预测容错控制方法。常规MPC在航天领域的研究大多用于根据不同场景约束设计相应的优化算法,解决控制或路径规划问题。相比于文献[23]所使用的常规MPC控制策略,显式模型预测控制方法对常规MPC进行了一定改进,能够将优化求解的在线计算放到离线进行,在线实施时只需查询状态量和控制量对应的仿射关系即可得出对应的控制量,能够降低计算量,更适用于在线过程[24]。现有研究中对于具备容错性能的MPC研究较少,文献[25]针对执行机构存在部分故障的线性系统,提出了一种基于闭环辨识的模型预测容错控制方法。文献[26]以吸气式高超音速飞行器为控制对象,当执行机构发生故障时,根据故障对参考控制指令进行二次重构,提出了一种基于模型预测控制策略的容错控制方法。上述研究中,对系统故障的处理均基于优化思想对执行机构的输出能力进行估计,受此启发,本文将引入MPC算法过程机制衍生出的一种先进状态估计方法——滚动时域估计(Moving horizon estimation,MHE)方法处理容错控制问题,该方法能够方便地处理系统的非线性特性,能够利用时域约束及测量信息进行在线估计。针对MHE的相关研究并不多见,文献[27]基于滚动时域估计理论和随机最小二乘理论,提出了一种分布式滚动时域估计算法,研究了数据传输丢失情况下的参数不确定无人机系统状态估计问题。当在轨服务航天器执行机构发生故障时,需要引入准确的系统模型才能解算使系统稳定的控制信号,此时需要引入一种基于在线数据的参数估计方法,提取系统发生故障后的模型参数,为MPC尽可能减少模型参数突变的影响,从而赋予MPC容错能力。与现有研究成果相比,本文的创新性可以总结为:针对航天器姿轨一体化控制问题,提出了一种基于姿轨一体化的显式模型预测控制策略,此外,将滚动时域估计方法与该模型预测控制方法相结合,提出了一种模型预测容错控制策略,共同实现执行机构输出效能退化情况下的航天器姿轨一体化容错控制。
综上所述,为了实现可靠稳定的卫星姿轨一体化容错控制,本文将利用MHE方法对执行机构的输出能力进行估计,同时与MPC相结合,从而实现模型预测容错控制策略。该方法能够在系统发生执行机构退化失效故障时迅速估计执行机构的输出能力,并在故障工况下完成对期望状态的跟踪,有效提高了卫星姿轨控制系统的实时性和可靠性。最后通过数值仿真验证了所提出控制方法的有效性,并通过与另一研究中的容错控制方法进行对照,体现了本文所提出方法的优越性。
1 相对姿轨一体化模型
1.1 坐标系定义及对偶四元数
首先定义相关坐标系,如图1所示。定义地心惯性坐标系O-XIYIZI的原点为地心,OXI轴在赤道平面内,方向由原点指向春分点,OZI轴垂直于地球赤道平面且与地球自转角速度矢量方向相同,OYI轴方向由右手法则确定。定义目标卫星本体坐标系O-XTYTZT的原点为目标航天器质心OT,三个坐标轴方向分别与航天器的惯量主轴重合。服务卫星本体坐标系O-XSYSZS定义与目标卫星一致。

图1 坐标系定义示意图
根据Chasles定理[28],刚体的运动可看作不经过原点的轴旋转并沿着该轴平移的合成螺旋运动。基于该螺旋运动的运动参数,由元素为对偶数的四元数表示,也可看作是元素为四元数的对偶数。具体描述为:

(1)
式中:qr,qd分别为对偶四元数的实部和对偶部。ε为对偶单位。
对偶四元数的运算法则与四元数类似,对于四元数运算法则和对偶四元数性质的详细介绍可参考文献[15]。本文关于所运用到的对偶四元数运算及相关定义如下:
四元数:
(2)
式中:θ为欧拉角;n为欧拉轴单位矢量。
矢量a=[a1,a2,a3]T的叉乘算子:
(3)
对偶四元数加法:
(4)
对偶四元数乘法:
(5)
式中:“∘ ”为四元数乘法运算,对偶四元数乘法的矩阵描述形式为:
(6)
式中:“[°]”表示为对应的乘法矩阵描述。
对偶四元数叉乘:
(7)
其矩阵描述形式由四元数叉乘运算得出,表示为:
(8)
对偶四元数的共轭:
(9)
对偶四元数的范数:
(10)

(11)

1.2 基于对偶四元数的姿轨一体化动力学
基于对偶四元数的误差运动学方程为:
(12)

基于对偶四元数的误差动力学模型方程为:
(13)

(14)
式中:m为质量,J为转动惯量。
为在该动力学模型中描述执行机构退化效能下降的故障,将控制输入对系统的对偶合力扩展为以下形式:
(15)
2 控制器设计
2.1 显式模型预测控制方法设计
为便于模型预测控制器设计,将基于对偶四元数的误差动力学与运动学整理成状态空间的形式。同时为了处理动力学中的冗余维度,可将该动力学系统状态空间形式记为
(16)
式中:
(17)
其中A(x)和B包含的矩阵运算算子为
(18)
采用前向欧拉法将该连续时变系统进行离散化,记为
x(k+1)=(A(x(k))·δt+I)x(k)+
(19)
基于式(19),可以递推出在k时刻下,预测时域为p的状态序列,记为
(20)
为方便后续优化过程描述,定义如下的状态序列和控制序列:
(21)
基于状态序列的预测方程为:
Xk=Ψx(k)+ΘUk
(22)
式中:
(23)
定义需跟踪的参考状态轨迹为:
Rk=[rT(k+1),…,rT(k+p)]T
(24)
此时,对于状态和控制量的代价函数可设计为:


(25)
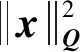
(26)
式中:Ξ⊆R14,υ⊆Rm+l,Ξf∈Ξ为状态容许集,控制约束集和终端约束集。上标*指代价函数最优时对应的参数值。通过求解该优化问题即可得到该显式模型预测控制策略的控制序列。
2.2 基于滚动时域估计的模型预测容错控制方法
基于式(16)的带有故障信息的系统模型可简写为:
(27)
对于卫星执行机构的故障在线辨识过程,需要由故障系统的历史状态数据和控制序列进行估计。本文通过引入滚动时域估计方法,采用系统测量的固定窗口的历史状态对控制量进行求解。将该固定窗口定义为估计时域NI。滚动时域估计方法通过优化求解如下辨识代价函数求解执行机构的故障系数:
(28)
式中:S为正定的对称矩阵,Υk为估计时域内的历史状态量和控制序列。
Υk={x(k-n),u(k-n)n=1,2,…,NI}
(29)
相似地,执行机构的故障系数序列可定义为:
(30)
该滚动时域估计器对于执行机构故障系数的估计可化为如下优化问题的求解:
(31)


图2 模型预测容错控制流程图
3 仿真校验
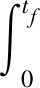

表1 仿真参数与初值
本文算例中服务星的执行配置选择了推力器和反作用飞轮的组合形式。服务星总计安装了4个可提供双向输出的推力器对及4个反作用力飞轮。
推力器和反作用飞轮的最大输出值分别为1 N和0.2 N·m。推力器和反作用飞轮的配置结构如图3所示:

图3 执行机构配置示意图
基于这种配置,服务星的对偶控制分配矩阵为:
模型预测控制器参数为

表2 故障工况下两种不同控制器对比

图4 故障情况示意图

图5 执行机构故障时状态响应及控制输出响应

图6 MHE故障估计性能曲线
需要说明的是,估计器在故障估计时产生了抖振,这是因为在模型预测控制器的作用下,所解算的力或力矩输出与上一时刻的控制输出方向相反且差值较大,表现为系统状态运行到状态拐点处。抖振后的估计系数仍能够快速收敛至准确的故障系数值。仿真表明,虽然受执行机构故障影响,系统收敛速度较执行机构完全正常时变慢,但是仍能保证收敛性能。总结来说,仿真结果证明了本文提出的算法具备执行机构故障时的容错能力,能够实现误差的快速收敛。
4 结 论
本文面向卫星在轨服务,基于对偶四元数框架下的姿轨一体化模型进行了模型预测容错控制方法研究。通过引入滚动时域估计器在线估计执行机构发生效率减退时的故障系数,设计了一种模型预测容错控制方法。最终通过数学仿真,验证了该控制方法在执行机构正常和故障两种工况下对卫星位置和姿态的跟踪控制能力,证明了所提出方法的有效性。
