利用凸优化方法的多航天器编队重构轨迹规划

刘幸川，陈丹鹤，徐 根，廖文和

(南京理工大学机械工程学院，南京 210094)

0 引 言

随着微小型航天器与分布式空间系统技术的发展,通过多航天器协同编队实现多类型、多维度的数据获取、融合处理及分析决策的创新理念[1],成为航天领域重要的研究热点。相比于单星庞大复杂的系统,由近距多航天器组成的编队或星群,具备更好的星地覆盖能力、在轨容错性及综合性能指标,甚至可完成单航天器难以实现的任务。同时多个微小型航天器组建的编队系统执行在轨任务,可大大降低系统复杂性、缩短研制周期、提高任务成功率[2]。因此,编队飞行领域受到国内外诸多专家学者的广泛关注,多项基于编队飞行的航天任务开展实施[3-4]。

航天器在轨飞行时,会受到多种摄动力的干扰,包括地球摄动引力、大气阻力、太阳光压及三体引力等。此外,航天器间特性参数的差异也会加剧星间的受力不均,如航天器迎风面质比。这些干扰会破坏编队的相对构型,降低初始捕获或者编队重构的精度。因此,考虑高精度的相对运动模型有利于提高轨迹优化的精度,而目前文献多以简化的HCW方程为相对运动模型。文献[5]参考地球同步轨道卫星中相对偏心率/倾角矢量分离的思路,使用相对轨道根数(Relative orbit elements,ROE)的方法描述多航天器的相对运动模型,该方法便于将J2摄动对编队几何构型的影响线性化处理[6],后续诸多学者基于此模型对J2～J6摄动、大气阻力差异等的影响进行研究,获得了较好的验证结果[7-9]。本文在相对运动建模时,考虑了J2～J6摄动与大气阻力差异的影响,以提高重构轨迹优化结果的精度。

多航天器编队任务,涉及到初始捕获、重构及编队维持等各阶段的相对轨道控制[10]。在控制过程中,需考虑诸多工程性约束,例如星间通信约束[11]、推力器推力幅值及缺省布置[12-13]、安全距离等。此外,航天器机动消耗燃料,这决定了轨道机动任务的寿命。因此,在重构过程中,在考虑上述约束的同时,燃耗越少表明设计的轨道机动路径最优[14-29]。目前,用于解决多航天器编队重构的轨迹优化方法有很多,包括庞特里亚金极小值原理(PMP)[14-16]、伪谱法[17-21]、混合整数线性规划(MILP)[22-24]、智能优化算法[18,24-27]、凸优化方法[27-29]等。

Li等[14]利用PMP推导了在双向推力器配置下的面内编队重构Bang-Bang控制方法。而后Mitani等[15]根据PMP与同伦平滑技术,研究在单向推力器开关常值推力约束与推力方向约束下的编队在轨道平面内的重构方法,并将其转换成两点边值问题后求解。文献[16]基于PMP方法,以两点边值的形式,解决了编队重构轨迹燃耗的问题,并以滑模变结构控制方法实现J2摄动下的轨迹跟踪控制。PMP在单航天器的轨迹优化方法中非常方便,但较难处理多航天器协同优化需求及动态优化中的防碰撞约束问题。

文献[17]使用Legendre伪谱法,将深空探测任务中多航天器编队重构问题离散化为非线性规划问题(NLP),然后通过KNITRO软件进行寻优求解,其中考虑了推力幅值约束和防碰撞约束。文献[18]结合Legendre伪谱法和智能优化算法中的协同进化粒子群优化算法,解决了深空三星编队重构轨迹优化问题,并考虑了重构过程中的安全距离约束。Wu等[19]将编队由跟飞构型重构为空间圆问题,通过Legendre伪谱法转换成NLP,并使用TOMLAB/SNOPT软件求解。文献[19]使用了包含J2摄动的非线性运动模型,并在STK软件中对优化结果进行了校验。Li[20]使用PMP方法推导基于HCW方程的必要优化条件,通过Radau伪谱法将其转换为NLP,并应用SNOPT软件解算。Li在算例中重点分析了比冲与推力幅值对优化结果的影响。岳晓奎等[21]利用伪谱同伦法求解了近地圆轨道三星跟飞构型的最优燃耗转移轨道,实现了Bang-Bang控制的平滑处理,但作者指出该方法计算难度较大,而文中也未考虑多航天器同时机动的安全距离约束。

Richards等[22]使用MILP给出一种航天器近距离操作燃耗最优机动轨迹的求解方法,并利用CPLEX软件求解。该文献将编队中其他航天器发动机工作时的羽流影响区域视为危险范围。Mauro等[23-24]基于文献[30]推导的常值连续小推力与ROE的映射关系及最优机动方案,以推力器工作时刻点和工作时间长度为优化变量,通过MILP方法(CPLEX求解)与粒子群优化方法分别求解了编队多轨飞行的重构轨迹优化问题。该方法虽可大大降低计算量,却不适用于多航天器协同优化过程中的安全距离约束。文献[25]针对航天器着陆小行星需求,使用深度神经网络实现了降落过程中防碰撞约束下的实时轨迹优化。Sarno等[26]围绕合成孔径雷达(Synthetic aperture radar,SAR)编队重构问题,利用遗传优化算法完成了多约束下重构最优路径规划,并对比了中心化和去中心化两种方法的计算耗时与燃耗情况。随后Sarno等[27]以遗传优化算法为上层,凸优化方法为底层,解决了SAR编队重构整体燃耗最优的机动任务规划问题。文献[28-29]基于编队飞行L波段孔径合成任务,使用凸优化方法规划了编队任务模式更迭时的转移轨迹。与其他方法对比,凸优化方法在约束处理、求解速度及精度方面具有较大的优势。

目前,针对近地圆轨道的多航天器编队飞行重构以及工程应用需求,亟需研究一种考虑摄动环境影响及实际工程约束的快速优化求解方法。本文根据多航天器编队重构机动任务,基于ROE推导了在J2～J6摄动与大气阻力差异摄动影响下的相对运动模型,考虑了微小型航天器的推力缺失、幅值约束及安全距离等工程约束问题,建立了使用凸优化方法求解的数学模型,实现了基于CVX软件的多航天器最优重构轨迹的寻优计算,有效地解决了在近地轨道摄动与多约束下的多航天器编队重构轨迹规划问题。

1 动力学基础

1.1 相对轨道根数

通过传统的开普勒轨道根数定义ROE[5],如下:

δα=f(α,ac,ic)-f(αc,ac,ic)=[δa, δλ, δex, δey, δix, δiy]T

(1)

f(α,ac,ic)=[a/ac,u+Ωcosic,ex,ey,i,Ωsini]T

(2)

式中:α=[a,e,i,Ω,ω,M]T是经典开普勒轨道根数,a为轨道半长轴,e为轨道偏心率,ω为近地点幅角,M为平近点角,u=ω+M为纬度幅角,Ω为升交点赤经,i为轨道倾角;ex=ecosω,ey=esinω;下标c表示参考星的开普勒轨道根数,d为伴随星轨道根数;参数δa,δλ,δe=[δex,δey]T与δi=[δix,δiy]T分别表示相对轨道半长轴、相对平均纬度幅角、相对偏心率矢量和相对倾角矢量。

1.2 考虑J2～J6摄动的相对轨道根数传播模型

文献[9]给出了ROE在J2～J6摄动引力下的传递矩阵的数值形式和推导方法,传播矩阵的数值形式如下所示:

ΦJ2～J6(αc, Δt)=

(3)

式中:

(4)

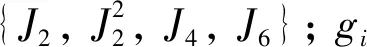
(5)

(6)

文献[31]推导了式(6)的具体表达式,本文直接引用并建立如式(3)的计算公式。因文章篇幅限制,本文不作介绍。

为验证ROE传播模型理论的准确性,本文使用GGM03引力场模型搭建6×6高精度轨道动力学仿真环境,用于对比ROE的传播模型理论值与试验仿真值,验证其准确性。轨道动力学环境中暂不考虑大气阻力的影响。试验参考轨道的初始轨道根数为[6 878.137 km, 0.001, 97.8°, 160°, 30°, 27°]T,初始ROE取acδα0=[0, -18.293, -28.534, -69.698, 57.451, -138.744]Tm,为半径r=150 m、相位角θ=30°的空间圆伴随航天器相对轨道参数。在高精度轨道动力学环境中,主航天器与伴随航天器以上述参数为输入值,使用RKF7(8)积分器获得绝对轨道状态,并依次计算瞬时根数、平均根数与ROE的试验参考值。理论计算值是以acδα0为输入值,通过式(3)的传播矩阵获得随时间变化的ROE。

图1给出了理论计算值与试验参考值的误差变化情况。由图1可知,经过17轨后,ROE中各元素的误差均较小,其中eacδλ最大,约为-0.23 m,这证明传播模型的理论精度较高,可满足较高精度的航天器编队轨迹规划需求。

图1 相对轨道根数传播模型的误差

1.3 ROE与相对位置速度的转换矩阵

当编队航天器的参考轨道为近地圆轨道时,伴随航天器的ROE参数与LVLH(local vertical local horizo-ntal)坐标系下的速度位置状态参量X的映射关系为:

X=M(u)acδα

(7)

式中:

(8)

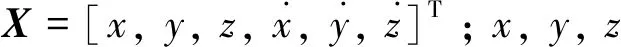
综上,可得相对位置速度状态在J2～J6摄动引力影响下随时间变化的计算方法,如下所示:

Xt+Δt=M(ut+nΔt)ΦJ2～J6(αc,Δt)M-1(ut)Xt

(9)

1.4 大气阻力差异摄动模型

近地轨道稀薄的大气层会对航天器产生气动阻力,是较为重要的摄动力。大气阻力属非保守力,始终作用在航天器上,量级虽小,但长时间的积累是不可忽视的。因此需在编队重构过程中考虑大气阻力差异带来的影响。大气阻力使在轨飞行的航天器受到与速度方向相反的加速度,加速度的大小与航天器的迎风面积、阻力系数、运动速度、质量与大气密度有关,可表示为

(10)

式中:ρ是航天器所在位置的大气密度;v是航天器相对于地球的飞行速度标量;S是航天器的迎风面积;m是航天器质量;CD是航天器的阻力系数;下标T表示沿航天器绝对速度方向。

因编队航天器间的距离较近,其所在位置的大气密度与绝对速度可视为相等,大气阻力摄动的差异仅与编队航天器间的固有属性相关。因此编队航天器间的大气摄动差异可表示为

(11)

2 基于凸优化的轨迹规划方法

多航天器燃耗最优的编队重构机动可定义为:在整体燃耗最小的情况下,各伴随航天器从其初始相对位置速度,通过轨道机动运动,在规定的时间点达到要求的终点相对位置速度。在机动过程中必须保证推力输出情况满足工程约束,航天器间的距离始终大于或等于安全距离。安全距离约束是一项非常重要的约束条件,其直接涉及到航天器的安全问题与任务执行。

2.1 问题描述

为便于处理航天器间的安全距离约束,本文使用相对位置速度作为计算参量,相对运动的一阶动力学模型可描述为

(12)

(13)

轨迹优化的目的是使得所有航天器寻找满足约束条件下最优的运动轨迹及控制输入u(t),并满足多航天器机动到指定位置且令整体燃耗最小。对于每个航天器,可使用如下目标函数描述:

(14)

式中:1阶范数表示将LVLH坐标系下三个方向的控制输入绝对值的总和作为燃耗目标函数。

通过边界约束条件令航天器的初始、终点状态满足任务要求,则这两个边界约束描述为:

(15)

式中:x0,j是第j个航天器的初始状态;xf,j是终点状态,即编队中航天器在任务结束时的相对状态。

在编队重构机动过程中,考虑存在的实际工程约束,即推力器推力幅值约束、配置约束及安全距离约束等。上述约束问题表达为:

(16)

式中:amax,j表示由推力器产生的最大加速度矢量;C=[I3×303×3]为计算第j个航天器的状态量xj(t)和第i个航天器xi(t)位置差值的提取矩阵;dsafe是为避免航天器间发生碰撞的最小安全距离。

2.2 数学模型建立

2.2.1单航天器数学模型的建立

(1) 时间离散:k=1, …,K(t1=t0且tK=tf);

(2) 时间步长:Δt=tk+1-tk;

(3) 机动时间:T=tK-Δt;

(4) 编队编号:j=1, 2, …,N。

这里假设在每个周期内,控制输入为恒定值。

2) 动力学模型离散化。通过拉普拉斯转换,将动力学的微分模型转换为非齐次模型:

(17)

(18)

本文采用包含J2～J6摄动影响的相对轨道根数传播模型为中间转移矩阵,即令:

(I+AΔt)=M(uk+1)ΦJ2～J6(αc,Δt)M-1(uk)=Φ

(19)

3) 目标函数。目标函数,或燃耗评估函数,同样离散化,在一个时间周期内的控制输入是连续分段式常值型输入,表达式为:

(20)

其中,1阶范数用于搜索燃耗最优的机动轨迹。

4) 边界条件。初始值与终点值即表示在初始时间与终点时间的航天器相对状态量,即:

(21)

对于编队中的任一航天器j,可通过该式约束初始与终点的相对位置与速度状态。

5) 加速度值约束。因为推力器输出值有限,导致航天器获得加速度值存在最大值约束,该约束问题可表述为:

(22)

当存在LVLH坐标系中±X方向存在推力器配置缺省时,上式可表示为

(23)

6) 安全距离约束。第i个航天器与第j个航天器之间的距离在编队重构过程中必须大于或等于最小安全距离,即:

(24)

这里i≠j。为保证在任意时刻(步长)内的安全距离,并且为更好地使用凸优化方法进行最优轨迹修正,将上式转换成[32]：

(25)

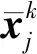
2.2.2多航天器数学模型的建立

本小节将离散化后的关系式汇总为多航天器编队重构过程的数学模型,以符合凸优化求解器的形式要求。控制系统的凸优化形式包括目标函数、等式约束与不等式约束等,即:

(26)

(27)

(28)

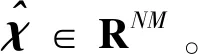
1) 动力学约束。对于航天器j,在k步的离散动力学系统模型可描述为:

(29)

则考虑k步时,将该式转换到状态转移矩阵与第j个航天器的状态量乘积表示为:

[06×9(k-1),-Φ, -BΔt,I6,06×9(K-k-1)]·

(30)

(31)

最后,离散系统动力学关系式在凸优化形式中的等式约束表达式为:

(32)

(33)

式中:j=1, 2, …,N。再汇总所有航天器的控制输入到统一的目标函数中,得到目标函数:

(34)

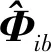
(35)

(36)

(37)

式中:xj,f表示第j个航天器的初始边界条件的列向量;xj,f是终点边界条件列向量。

4) 加速度约束。对于每个航天器j,推力器的配置约束及幅值约束由下式表示:

(38)

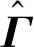
(39)

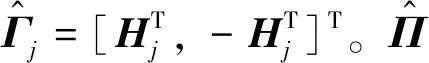
(40)

5) 安全距离约束。因每个航天器均在进行机动,所以安全距离的计算需要进行实时的动态计算,其计算表达式为:

(41)

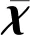
(42)

式中:

(43)

2.3 凸优化求解

本文使用CVX软件求解凸优化问题。CVX软件由CVX Research开发,能够快速求解凸优化问题,并且可免费用于研究。用户可选择SDPT3,SeDuMi或者GuRoBi方法求解,求解精度分为5种模式,精度由低到高分别是:low,medium,default,high,best。

3 仿真校验

3.1 场景设计

本文构思了一种多航天器编队重构场景,来验证本文方法解决转移轨迹优化问题的有效性及高效性。重构需求如图2所示,假设初始参考轨道根数是[6 878.137 km, 0.001, 97.8°, 160°, 30°, 27°]T,编队航天器数量为5个。在初始构型中,1、2、3号航天器构建成50 m空间圆构型,相位分别为0°、120°、240°,4、5号航天器分别落后绕飞中心点100 m、150 m。目标编队是50 m投影圆构型,5个航天器相位均布,相位顺序为1、2、4、3、5,此时相位分别为-42°、30°、102°、174°、246°。图中仅给出了LVLH坐标系下XY平面投影示意图。该场景任务包括“进入编队”与“由空间圆重构为投影圆”两个典型编队重构模式。仿真场景中各航天器的特性参数及仿真设置参数如表1所示。

表1 各航天器的特性参数及仿真参数

图2 编队重构任务XY面投影示意图

3.2 仿真结果

通过对上述场景进行仿真校验,获得仿真结果,如图3～图6所示,包括相对转移轨迹、星间距离与推力加速度值。

图3 所有约束下的最优转移轨迹

图3给出了各航天器所有约束下最优转移轨迹结果,包括LVLH坐标系下的三维图像、XY平面轨迹投影及YZ平面轨迹投影。

图4表示不考虑安全距离约束时,5个航天器之间的距离变化曲线,即寻优计算1的优化结果,安全距离由黑色虚线表示。由图4可知,在1 500～2 500 s时间范围内,2号与4号航天器的距离小于40 m,未满足安全距离约束。图5表示考虑安全距离约束时,各航天器之间的距离变化曲线,即寻优计算2的求解结果。图5表明,在考虑安全距离约束的情况下,2号与4号航天器之间的相对距离满足大于40 m安全距离的要求,这说明优化结果满足航天器间安全距离的约束条件。

图4 无安全距离约束时相对距离变化图

图5 存在安全距离约束时相对距离变化图

本文仅给出4号航天器在LVLH坐标系下两次优化结果的推力加速度输出值,如图6所示。图中,灰色虚线表示推力器所能输出的最大加速度值,红色方形实线表示X向加速度输入值,黑色菱形虚线为Y向加速度,蓝色圆形实线是Z向加速度。由图6可知,两次优化结果的X方向不存在推力加速度输出,仅在Y向、Z向存在推力输出,且最大值小于或等于最大加速度约束值。当考虑安全距离约束时,图6(b)的Z向加速度输入值发生改变。

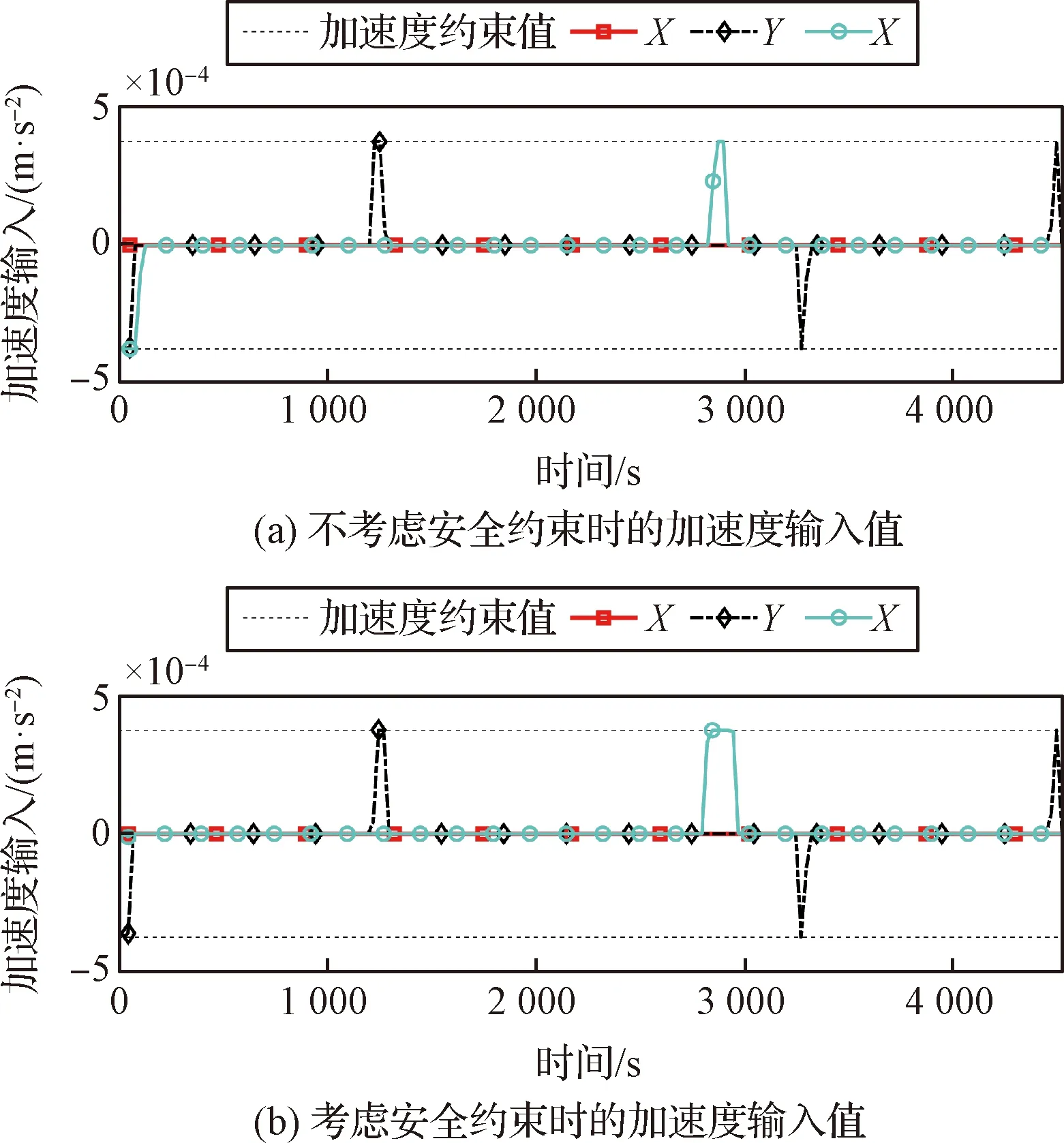
图6 4号航天器的优化加速度输入值

为更好地验证动力学迭代过程的精度,本文通过下式对寻优结果中各航天器的动力学迭代精度情况进行统计:

(44)

结果如表2所示,不考虑安全约束的优化计算精度量级均为10-13,考虑安全约束时的优化计算精度量级均为10-9,而文献[17]中的精度仅为10-4。由此可知,考虑安全距离约束情况的优化求解精度比不考虑时低,但二者整体精度值都比较高,说明该方法具有较好的动力学精度。

表2 动力学约束精度

文献[29]利用凸优化方法提出一种完全基于ROE解决编队重构机动规划的方法,并在算例中求解5个航天器由前后跟随构型重构为空间圆形构型的机动轨迹优化方案。与之对比,算法求解效率差异在表3中给出。由表3可知,本文方法在寻优计算方面速度较快。此外,本文方法同文献[17]的伪谱法及文献[20]的NLP方法对比,具有更快的求解速度。

表3 算法求解效率对比

4 结 论

本文提出一种使用凸优化的近地圆轨道多航天器编队重构最优转移轨迹优化方法,该方法解决了在地球引力摄动与大气阻力摄动对相对运动的影响以及航天器推力缺省、幅值约束与安全距离等工程约束下的编队重构轨迹规划问题。

本文根据J2～J6摄动引力对平均轨道根数的摄动影响,建立高阶摄动对ROE的传播矩阵,并给出了ROE与相对位置速度状态的转换关系以及大气阻力差异摄动对相对运动的映射关系。将航天器推力缺省配置约束、推力器输出幅值约束及多航天器编队重构过程中的安全距离约束等问题,转换成使用凸优化方法求解多星最优转移轨迹的数值形式,并在文中给出了使用CVX软件求解上述约束问题下多航天器编队重构轨迹的优化计算方法。最后利用凸优化方法解决任务需求的多星编队重构转移轨迹优化问题,对轨迹优化问题的求解速度与计算精度进行对比分析。结果表明,所提方法获得的编队重构最优转移轨迹能够较好地满足所述约束条件,而且具有计算速度快、精度高的优点。可为多航天器协同编队重构提供理论及工程应用基础。