带线性记忆的Kirchhoff型耦合吊桥方程的指数吸引子
2023-07-21姜金平王思博
王 雪, 姜金平, 王思博, 魏 佳
(延安大学 数学与计算机科学学院, 延安 716000)
0 引 言
考虑带线性记忆的Kirchhoff型耦合吊桥方程
(1)
指数吸引子的存在性。其中α,β>0,k2(u-v)+是恢复力,k表示弹性系数,μ表示记忆核,函数(u-v)+=max{(u-v),0},外力项g1(x),g2(x)∈L2(Ω),Ω是2内光滑边界∂Ω的有界开区域。对于吊桥方程和指数吸引子的一些问题已被很多学者研究[1-18];1990年,Lazer等首次提出耦合吊桥方程[1]
2018年,贾澜等利用算子分解的方法研究了带强阻尼的Kirchhoff型吊桥方程
指数吸引子的存在性[3]; 2019年,王美霞等通过紧性平移定理及构造三元解相空间研究获得了带记忆项的Boussinesq方程

指数吸引子的存在性[4]; 2022年,王彩霞等利用能量估计和算子分解的方法研究了带记忆项和线性阻尼的Kirchhoff梁方程
指数吸引子的存在性[5]。Kirchhoff型耦合吊桥方程比单个吊桥方程更加全面的考虑了其桥面的可拉伸性和主链的运动情况,但是对于Kirchhoff型耦合吊桥方程指数吸引子的研究很少,故基于以上文献的启发,本文构造三元解相空间将算子分解的方法应用于耦合类的方程中,对恢复力k2(u-v)+进行新的处理,研究得到了带线性记忆的Kirchhoff型耦合吊桥方程指数吸引子的存在性。
1 预备知识
首先需将问题(1)转化成确定的自治系统,根据文献[7-8]的启发引入历史位移变量
η=ηt(x,s)=u(x,t)-u(x,t-s),γ=γt(x,s)=v(x,t)-v(x,t-s), (x,s)∈Ω×+,t≥0
则

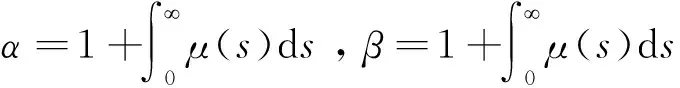
(2)
边值条件为
u(x,0)=u0(x),ut(x,0)=u1(x),ηt(x,0)=0,η0(x,s)=η0(x,s)
v(0)=v(L)=0, (x,t)∈Ω×+,γ=γ(L)=0, (x,t,s)∈Ω×+×+
v(x,0)=v0(x),vt(x,0)=v1(x),γt(x,0)=0,γ0(x,s)=γ0(x,s)
其中
不失一般性,定义Hilbert空间族Vs=D(As/4),定义其范数和内积为
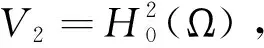
用||Au||表示D(A)的范数,其中
显然,
式中:
分别是H、V1的对偶空间。特别地,有紧嵌入Vs+1⊂Vs和Poincare不等式
式中λ1是Δ2在D(A)中的第一特征值。
设方程(1)中的非线性函数f∈C(,)满足条件
(H2)|fi(s)|≤C(1+|s|p),∀s∈,p≥1,i=1,2
由条件(H1)和条件(H2)可知,存在正常数K1、K2、K3和K4,η=η(λ1)>0,γ=γ(λ1)>0,使得
f1(s)s+ηs2+K1≥0,F1(s)+ηs2+K2≥0,∀s∈
(3)
f2(s)s+γs2+K3≥0,F2(s)+γs2+K4≥0,∀s∈
(4)
设方程(1)中的记忆核函数μ(·)满足条件
(H3)μ∈C1(+)∩L1(+),μ′(s)≤0≤μ(s),∀s∈+

由条件(H3)、(H4)定义如下Hilbert空间

并在M上定义线性算子T,定义域为
D(T)={η,γ∈M|∂sη,∂sγ∈M,η(0)=0,γ(0)=0}
式中:Tη=-∂sη,Tγ=-∂sγ,∀η,γ∈D(T),∂sη表示η关于内部变量s的分布导数,∂sγ表示γ关于内部变量s的分布导数,则D(T)空间上的内积可定义为
(η1,η2)D(T)=(η1,η2)M+(∂sη1,∂sη2)M, (γ1,γ2)D(T)=(γ1,γ2)M+(∂sγ1,∂sγ2)M
定义1[6]给定η∈L,η在L中的尾部函数是Tη:[1,∞)→[0,∞),定义为
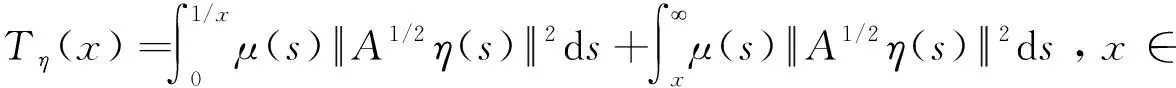
同样可定义
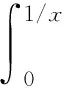
引理1[6]若C⊂L满足下列条件:
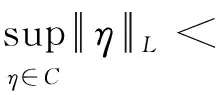

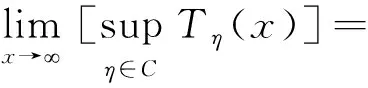
则C在L中相对紧。
记
且范数分别为:
((u1,v1,η1),(u2,v2,η2))V=(u1,u2)V2+(v1,v2)H+(η1,η2)L
((u1,v1,η1),(u2,v2,η2))VT=((u1,v1,η1),(u2,v2,η2))V+(∂sη1,∂sη2)M
定义2(指数吸引子)[3]如果集合M⊂X,X为完备度量空间,满足下列条件:
(1) 集合M在X中具有有限维的分形维数且是紧的;
(2) 集合M是正不变的,即S(T)M⊂M;
(3) 集合M为半群的指数吸引集,即对每一个有界集B⊂X,存在常数k=k(B),l>0,使得dist(S(T)B,M)≤W(||B||X)e-lt,其中{S(T)}t≥0为完备度量空间中X的半群,则集合M为半群{S(T)}t≥0的指数吸引子。
引理2[3]设Χ⊂H是一不变紧子集,且W到H是紧嵌入,存在时间t*>0,使得如下条件成立:
(1) 映射{(t,z0)S(T)}: [0,t*]×Χ×Χ是Lipschitz连续的;
(2) 映射S(t*):Χ→Χ有如下分解:
S(t*)=S0+S1,S0:Χ→H,S1:X→W
式中S0满足
S1满足
||S1(z1)-S2(z2)||W≤C*||z1-z2||H
则半群S(t*):X→X存在指数吸引子。
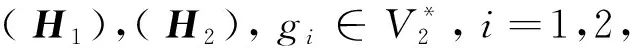
(1) 若初值(u0,v0,u1,v1,η0,γ0)∈H,那么问题(2)有一个弱解
(u,v,ut,vt,ηt,γt)∈C([0,T],H),∀T>0
并且满足

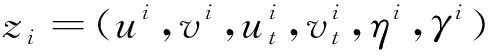
|z1(T)-z2(T)|H≤ect|z1(0)-z2(0)|H,t∈[0,T]
因此,问题(2)存在唯一的弱解(u(T),v(T),ut(T),vt(T),ηt,γt),定义算子S(T):H→H为
S(T)(u0,v0,u1,v1,η0,γ0)=(u(T),v(T),ut(T),vt(T),ηt,γt),t≥0
算子S(T)满足半群的性质且可定义一个在H上局部Lipschitz连续的非线性C0半群。
2 有界吸收集
2.1 H中的有界吸收集
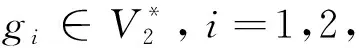
证明取0<ε<1,在空间中用φ=ut+εu和ψ=vt+εv与问题(2)中的两个方程分别作内积,整理得到
-ε(1-ε)(u,φ)+ε||Δu||2+(ηt,ut)M+ε(ηt,u)M+ε||∇u||2+ε||∇u||4
+(1-ε)||ψ||2-ε(1-ε)(v,ψ)+ε||∇v||2+(γt,vt)M+ε(γt,v)M
+(k2(u-v)+,φ-ψ)+(f1(u),φ)+(f2(v),ψ)
=(g1(x),φ)+(g2(x),ψ)
(5)
式中
(6)
(7)
(8)
由式(2)、Holder不等式和条件(H4)得
(9)

(10)
利用Holder不等式、Young不等式和Poincare不等式得
(11)
将式(6)~式(11)代入式(5),整理后得到
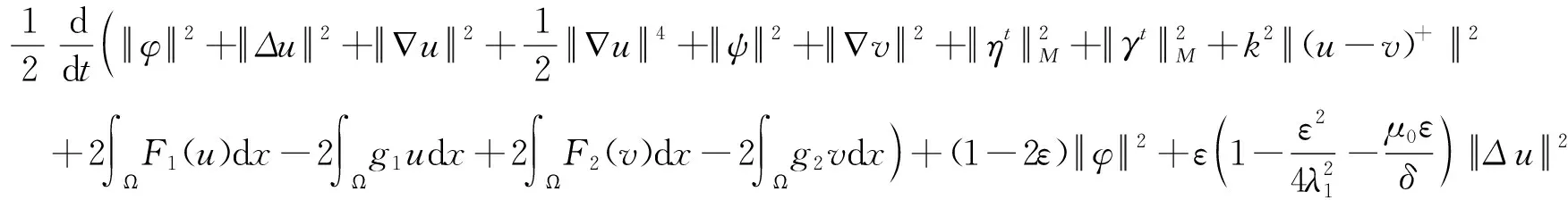
≤0
(12)
令
(13)
≤0
(14)
根据式(3)、式(4)及Sobolev紧嵌入定理,有
(15)
式中:
同理可得
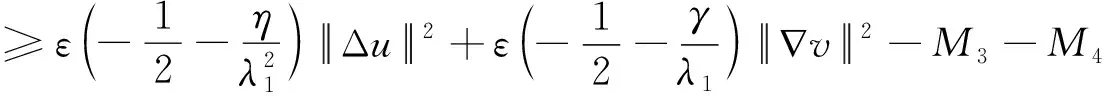
(16)

将式(15)和式(16)分别代入式(13)和式(14),得

(17)

(18)
取ε,η,γ充分小,令
则
E(T)≥C1(||φ||2+||Δu||2+||∇u||2+||∇u||4+||ψ||2+||∇v||2
(19)
(20)
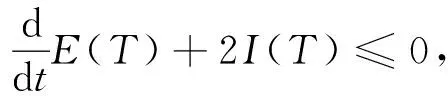
+k2||(u-v)+||2)-M3-M4]dτ+E(0)
(21)
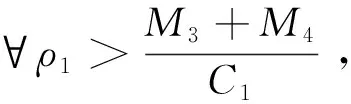

B1={(u0,v0,u1,v1,η0,γ0)∈H:||u1+εu0||2+||Δu0||2+||∇u0||2+||∇u0||4
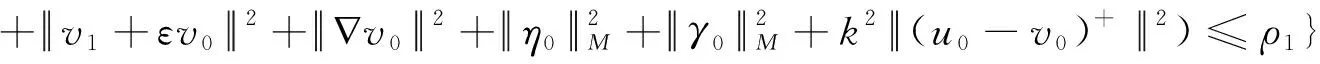
(22)
则B0是半群{S(T)}t≥0的一个有界吸收集。
2.2 VT中的有界吸收集
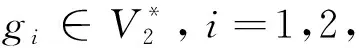
||z0||VT=||u0,v0,u1,v1,η0,γ0||VT≤ρ1
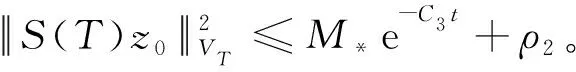
证明在空间中用-Δφ=-Δut-εΔu和-Δψ=-Δvt-εΔv与问题(2)中的两个方程分别作内积,整理得到

-ε(1-ε)(∇u,∇φ)+ε||Δ∇u||2+(ηt,ut)L+ε(ηt,u)L+ε||Δu||2+ε||∇u||2||Δu||2-||Δu||2(∇u,∇ut)
+(1-ε)||∇ψ||2-ε(1-ε)(∇v,∇ψ)+ε||Δv||2+(γt,vt)L+ε(γt,v)L+(k2(u-v)+,-Δφ)
-(k2(u-v)+,-Δψ)+(f1(u),-Δφ)+(f2(v),-Δψ)
=(g1(x),-Δφ)+(g2(x),-Δψ)
(23)
由Poincare不等式、Holder不等式、Young不等式、推论1中的有界性和式(22)可得
(1-ε)||∇φ||2-ε(1-ε)(∇u,∇φ)+ε||Δ∇u||2-||Δu||2(∇u,∇ut)+(1-ε)||∇ψ||2-ε(1-ε)(∇v,∇ψ)+ε||Δv||2
(24)
事实上,有||((u-v)+)t||≤||(u-v)t||,即可得
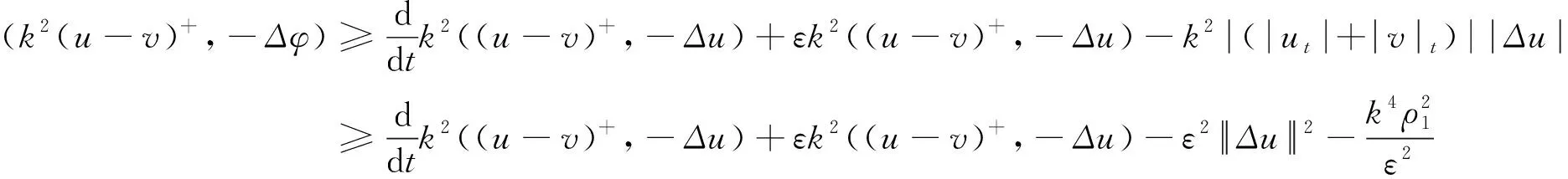
(25)
同理
(26)
利用Sobolev嵌入定理可得,存在K>0,使得
||f(i)||L∞ 有 (27) (28) 将式(24)~式(28)代入式(23)整理,得到 (29) 取ε>0,令 则式(29)可进一步改写为 (30) 令 则有 其中 由Gronwall引理可得 P(T)≤C2P(0)e-C2t+c1 (31) 由范数的等价性可得 (32) 所以由式(31)和式(32)得 (33) 根据文献[4-5]可知,||∂sγ||、||∂sη||一定有界,其中γt(0)=0,ηt(0)=0且 (34) 故由式(33)和式(34)可知结论成立。 引用文献 [6]中不变紧集的概念,设x*=x*(μ)≥1,当满足x≥x*时,下式成立: (35) 根据定理2及推论2,可令 则∃tΝ>0,使得当t≥tΝ时,S(T)Β⊂Ν。 定理3对任意初值z1=(u10,u11,v10,v11,η10,γ10),z2=(u20,u21,v20,v21,η20,γ20)∈H,对∀R>0当||zi||H≤R(i=1,2)时,存在一个与ε,λ1,ρ1,K,c4有关的常数P,有 ||S(T)z1-S(T)z2||H≤P||z1-z2||H,∀t∈+ (36) (37) (38) 其中 (39) 由Sobolev嵌入定理、Holder不等式、Young不等式、Poincare不等式及Minkowski不等式可得 (40) 同理可得 (41) (42) 同理 (43) 且 (44) 将式(39)~式(44)代入式(38),整理得 (45) 进一步估计,可得 (46) 式中P是与ε、λ1、ρ1、K、c4有关的常数,最后利用Gronwall引理即可证明此结论。 定理4存在正常数M,且z0=(u0,u1,v0,v1,η0,γ0),z(T)=(u(T),v(T),ut(T),vt(T),ηt(s),γt(s))使得 (47) (48) 由Sobolev嵌入定理、Holder不等式、Young不等式、Poincare不等式及Minkowski不等式可得 (49) (50) (51) (52) (53) 将式(49)~式(53)代入式(48)整理得 (54) 取ε充分小,使得 令 (55) 利用Gronwall及定理1得 (56) 从而证得定理4,即 式中M>0。 定理5映射{(t,z0)S(T)}: [0,T]×X×X是Lipschitz连续的,其中∀T>0。 证明对任意的t1,t2∈[0,T],z1,z2∈Χ,有 ||S(t1)z1-S(t2)z2||H≤||S(t1)z2-S(t2)z2||H+||S(t1)z1-S(t1)z2||H (57) 对于||S(t1)z1-S(t2)z2||H这项,由定理4可得 (58) 对于||S(t1)z1-S(t2)z2||H这项,由定理3可得,存在L=L(T)≥0,使得 ||S(t1)z1-S(t2)z2||H≤L(|t1-t2|+||z1-z2||H) (59) 综上证得定理5成立。 定义线性空间 定理6设Z到H是紧嵌入的,且Χ⊂H是一不变紧子集,则存在C*>0和时间t*>0,使得映射S(t*):Χ→Χ有如下分解: S(t*)=S0+S1,S0:X→H,S1:X→Z 式中S0满足 S1满足 ||S1(z1)-S2(z2)||W≤C*||z1-z2||H (60) (61) =0 (62) 由Holder不等式、Young不等式以及Poincare不等式作类似估计得 ≤0 (63) 定义泛函 (64) 取ε充分小得 (65) 式中a为正常数。取 可得 根据式(65),上式变为 由式(65)和Gronwall引理得 =0 (66) 式中 (67) 由Sobolev嵌入定理、Holder不等式、Young不等式、Poincare不等式及Minkowski不等式可得 (68) 同理可得 (69) 作与式(42)类似估计得 (70) 同理 (71) 且与式(43)估计方法相同得 (72) 将式(67)~式(72)代入式(66),整理得 (73) 取ε充分小,则 (74) (75) 接下来还需证明记忆项满足 (76) (77) 结合定理1~定理6即可得到问题(2)指数吸引子的存在。 对于带线性记忆的Kirchhoff型耦合吊桥方程,为了得到其指数吸引子的存在性,普通的证明方法,例如加强的平坦性条件大弱,不能够证明含有记忆项方程的解半群的紧性,所以需要构造三元解相空间,利用算子分解的方法来证明其指数吸引子的存在性。通过对定理1到定理6的证明即可得到问题(1)指数吸引子存在。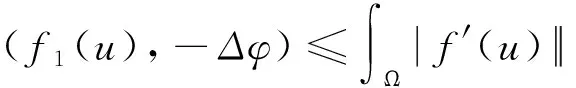
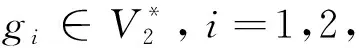
3 指数吸引子的存在性

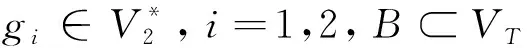

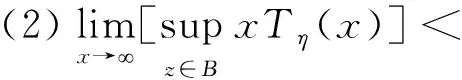

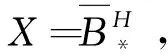
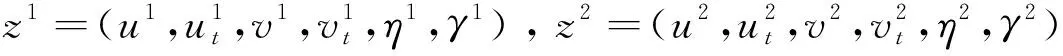
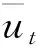
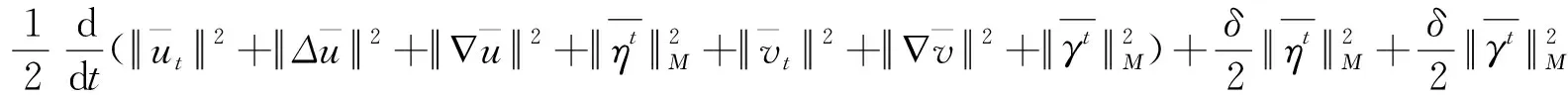





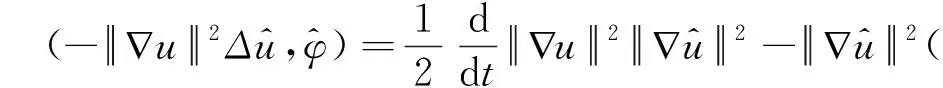



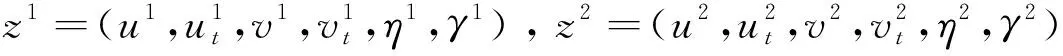

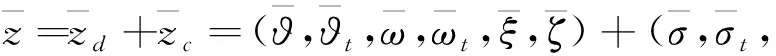
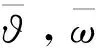
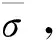
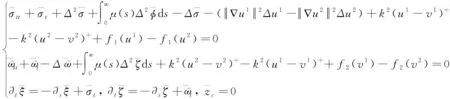
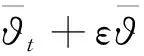
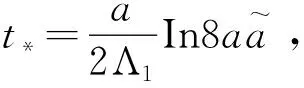

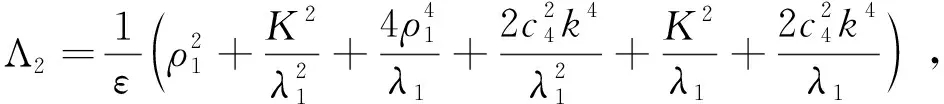

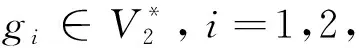
4 结 论
