椭圆形液体润滑轴承承载特性的研究
2023-07-21郭强
郭 强
(太原重工油膜轴承分公司,太原 030024)
1 液体润滑轴承承载机理
液体动力润滑是利用粘性液体能够牢固地粘附在机械表面,机械运转时,液体被带入机械间隙中的作用实现的。当机械表面间隙呈收敛形时,进入间隙中的液体压力会逐渐增大[1],当液体的粘度和机械的转速、负荷、间隙等配合恰当时,在液体中就能产生较高的压力,使两个摩擦面分开,也就是说,液体动力润滑不需借助外力作用,而靠部件本身运动,在摩擦表面间建立一高压油膜,使摩擦面分开,减少机械表面的摩擦和磨损。液体动力润滑使用的润滑剂主要是润滑油,从润滑油的性质方面来说,主要作用的是润滑油的粘度[1]。图1为液体动压润滑的原理示意图,轴承与旋转轴之间充满了不可压缩的,动力粘度为η的润滑油。负荷加在旋转轴上,在轴以角速度ω旋转时,在载荷W的作用下,轴心O和轴心O′相互偏离,O和O′之间的距离e称为偏心距,OO′的连线和载荷W的夹角φ称为偏位角。由于润滑油具有一定的粘度,润滑油随着轴的旋转进入到间隙内,顺着旋转方向,间隙越来越小,润滑油被挤压而产生压力,直到间隙最小处,润滑油被挤压的越来越厉害,油膜压力越来越大,这些油膜压力的总和就形成轴承的承载力并与外载荷W平衡。经过间隙最小处后,间隙越来越大,润滑油不再被挤压,油膜的压力逐渐消失[2]。

图1 液体动压润滑原理示意图Fig.1 Schematic diagram of the liquid dynamic pressure lubrication principle
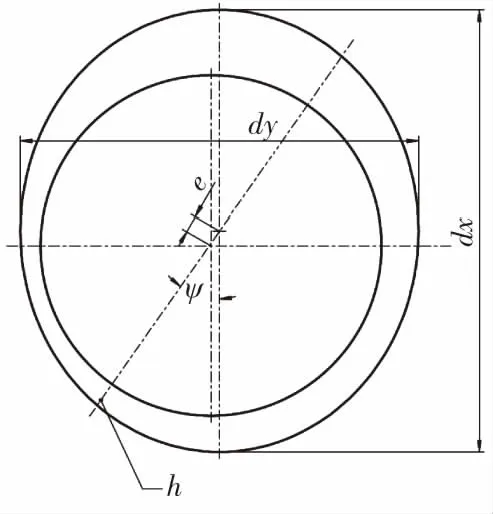
图2 椭圆形轴承示意图Fig.2 Schematic diagram of the elliptical bearings
2 液体动力润滑轴承承载的计算
假设轴与轴承间形成了完整的压力油膜,轴中心O偏离轴承中心O′,两者的距离OO′称为偏心距e,偏心距延长线将油膜分为两部分,油膜的收敛区域和发散区域。在收敛的油膜区域中,油膜产生了足够的压力P平衡了负载W,使轴在油膜上运转。
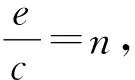
h=c(1+ncosφ)
(1)
对于圆形液体润滑轴承,油膜轴承的承载可以根据雷诺方程得出:
(2)
滑动轴承在工程中起着定位和承载的作用,润滑油在滑动轴承偏心区域能形成动压效应,其合力与外部的载荷相平衡,当轴承处于稳定运行状态时,载荷的各方向上合力为0,即:
∑Fx=0,∑Fy=0


由于求解油膜承载需求解上述方程,求解过程中积分运算比较复杂,因此工程上常采用数值分析法或者CFD(计算流体动力学)来求解。椭圆形液体润滑轴承同样也满足上述平衡方程,为了将求解简单化,采用CFD仿真技术。
目前国内对于液体润滑轴承的计算多采用数值仿真计算,涉及到的轴承偏心率均低于0.8,轴承的转速也相对较高,此时液体润滑轴承形成的油膜相对较厚,对于在复杂工况下,低速重载轴承,过低的偏心率无法满足轴承承载要求,如果为了提高承载降低轴承的名义间隙会影响轴承的散热功能。为了满足承载,轴承偏心率均高于0.9.
本文通过利用CFD流体动力学仿真技术,完成了高偏心率下的油膜流场求解,通过仿真得出了高偏心率下的油膜压力分布和承载能力,对实际轴承的选型设计提供了理论指导。
3 椭圆形轴承的CFD仿真前处理
对于椭圆形液体润滑轴承来讲,由于其曲率发生变化,很难利用传统的微分方程描述出椭圆形轴承承载的方程,因此可以利用CFD仿真技术来模拟计算椭圆形轴承的承载能力和承载区的油膜压力分布[4],为了建模方便,可以假定模拟椭圆形轴承的长轴做为变量,短轴不变的模型。长轴的偏心距为0时相当于圆形轴承,偏心距变化范围设定为(0~0.4)mm.
为了研究椭圆形液体润滑轴承的承载性能,选择相同规格型号的圆形轴承做对比。圆形液体润滑轴承的参数设定为:轴颈直径为1 065 mm,轴承长度为800 mm,轴颈转速为40 rpm,定义油膜厚度为20 μm.轴承的直径间隙为1 mm.对于圆形轴承,最小油膜厚度为20 μm,此时对应的轴承偏心率为0.96.
图3为利用CFD仿真软件求解计算液体润滑轴承的流体域模型和边界条件设定,在该模型中包含了轴承的几何尺寸和油膜厚度的特征。

图3 油膜流体域模型和边界条件Fig.3 Oil membrane fluid domain model and boundary conditions
当液体润滑轴承开始运转时,轴颈与轴套之间的间隙中会存在着油膜的收敛区域和发散区域,在对所定义流体域模型仿真时,应当预计到油膜可能在扩散区内自然破裂,因此油膜完整区的终止边界以及整个压力分布会在边界处形成突变,具体的表现为液体滑动轴承在工作过程中,油膜的发散区域会形成负压区域,使润滑油产生空穴效应。因此必须在仿真计算过程中考虑到实际会产生的空穴效应,采用多相流空化模型[5],在该液体润滑轴承的仿真过程中,采用的是Singhal et al.空化模型,多相流中定义相的数目为二相,分别为:主相Primary Phase为液相,液体密度为860 kg/m3,液体的运动粘度Viscosity为0.395 6 kg/m·s,第二相Secondary Phase为气相,气体为空气。
为实现对病害的有效控制,在蔬菜生产过程中应采取嫁接换根的方式,如将黄瓜与黑子南瓜相嫁接,便可有效抑制黄瓜枯萎病的发生。
滑动轴承运行过程中产生的空穴现象,主要是因为溶解在润滑油内的空气由于外界压力变低,其体积膨胀析出所造成的。在边界条件的处理上,设定如下:
A:液体润滑轴承入口边界条件,定义入口边界条件的形式为压力入口边界条件(inlet),压力大小为1E5 Pa.
B:液体润滑轴承出口边界条件,定义出口边界条件的形式为压力出口(outlet),设置出口压力为0.
C:旋转壁面边界条件(rotation Wall),定义旋转壁面的转速为40 rpm.
D:固定壁面边界条件(Wall).
完成油膜流体域模型的建立之后,需要对该流体域进行离散化,即通过划分网格的方式,将流体域模型离散化为由单元和节点构成的有限元模型。由于该流体域有着极高的偏心率,因此需要流体域几何模型其进行特殊处理的方式来划分网格。
CFD模拟分析计算,需要将油膜流体域通过网格划分离散化,仿真的准确性依赖于划分网格的质量,而油膜流体域的几何形状决定了网格划分非常困难(油膜长度方向和厚度方向的尺寸相差极大,长度尺寸为1 000 mm左右而厚度方向仅仅为25 μm(2.5E-3 mm)甚至更小),因此网格划分过程中需要处理好“跨尺度”的问题。
通过对油膜轴承分析计算的研究,可以得出非结构化网格(四面体单元)划分的油膜流体域,在计算过程中不能得到很好的收敛。因此在流体域离散化过程中需要采用结构化网格(六面体单元)[6],为了得到高质量的网格,通过对流体域进行分割,得到可以划分成为六面体网格的区域,为了得到极薄油膜厚度下的网格,往往需要将流体域做出十几次的分割,而随着油膜厚度的变化,分割方法也会随之产生变化。通过对网格划分的研究,目前可以完成最高偏心率为0.998,油膜流体域的结构化网格划分。并且能够控制很好的网格质量,单元畸变度skewness平均值为0.26.
4 CFD仿真后处理结果分析
图4为圆形液体润滑轴承CFD仿真完成之后得出的油膜压力分布图,可以看出,油膜流体域整个承载区域压力分布完整的呈现出来,并未出现不连续离散的形貌,进而验证了在仿真迭代的过程中计算中得到了很好的收敛。油膜中心区域的最高压力值为144 MPa,此时轴承能够提供的载荷为1 941 t.

图4 圆形液体润滑轴承油膜压力分布图Fig.4 Oil membrane pressure distribution diagram of circular liquid lubrication bearing
图5为椭圆形液体润滑轴承椭圆度0.1 mm时的油膜压力分布,此时轴承的工作区椭圆长轴偏心距0.1 mm,非工作区偏心距为0.油膜中心区域最大压力值为162 MPa,油膜能提供的载荷为2 319 kN.从仿真可以得出,当液体润滑轴承工作区存在偏心距时,相比圆形液体润滑轴承,承载能力增加。

图5 椭圆度0.1 mm时油膜压力分布图Fig.5 Distribution diagram of oil membrane pressure at an ellipticity of 0.1 mm
图6为椭圆形液体润滑轴承椭圆度0.2 mm时的油膜压力分布,此时轴承的工作区椭圆长轴偏心距0.2 mm,非工作区偏心距为0.油膜中心区域最大压力值为169 MPa,油膜能提供的载荷为2 698 t.

图6 椭圆度0.2 mm时油膜压力分布图Fig.6 Distribution diagram of oil membrane pressure at an ellipticity of 0.2 mm
图7为椭圆形液体润滑轴承椭圆度0.3 mm时的油膜压力分布,此时轴承的工作区椭圆长轴偏心距0.3 mm,非工作区偏心距为0.油膜中心区域最大压力值为185 MPa,油膜能提供的载荷为2 922 t.

图7 椭圆度0.3 mm时油膜压力分布图Fig.7 Distribution diagram of oil membrane pressure at an ellipticity of 0.3 mm
图8为椭圆形液体润滑轴承椭圆度0.4 mm时的油膜压力分布,此时轴承的工作区椭圆长轴偏心距0.4 mm,非工作区偏心距为0.油膜中心区域最大压力值为193 MPa,油膜能提供的载荷为3 320 t.

图8 椭圆度0.4 mm时油膜压力分布图Fig.8 Distribution diagram of oil membrane pressure at an ellipticity of 0.4 mm
图9为椭圆形轴承油膜轴心压力、椭圆形轴承承载能力和轴承椭圆度的关系曲线,从曲线上可以看出,随着轴承椭圆度的增加,轴承油膜中心压力和轴承的承载能力增大。从仿真计算中可以得出,当轴承椭圆度增加0.4 mm时,相比圆形轴承承载能力提高了71%,油膜中心的压力增加了34%.

图9 轴承椭圆度和中心压力、承载能力关系曲线Fig.9 Relationship curve between bearing ellipticity and central pressure and bearing capacity
因此在一些特殊的工况场合,轴承处于低速重载工况时,为提高轴承的承载能力,可考虑设计椭圆形液体润滑轴承替代圆形液体润滑轴的方案,增大轴承的承载能力。
相比圆形轴承,椭圆形轴承的端泻面积增加,工作过程中需要的供油流量也会增大。图10为轴承工作区椭圆度和润滑油流量的关系曲线,因此在使用椭圆形轴承替代圆形轴承增加承载能力的同时,需要增加供油流量。当椭圆形轴承椭圆度为0.4 mm时,轴承供油流量相比圆形轴承增加了24%.
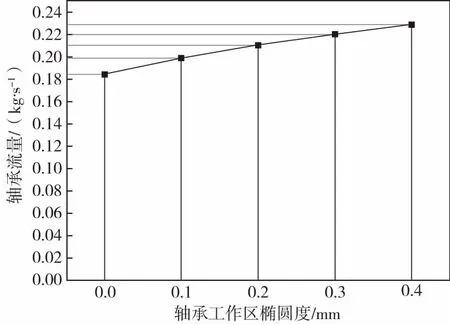
图10 轴承椭圆度和供油流量关系曲线Fig.10 Relation curve of bearing ellipticity and oil supply flow
5 结论
(1)确定了椭圆形液体润滑轴承椭圆的椭圆度和承载能力,油膜中心压力变化的规律。对处于低速重载运行的液体润滑轴承,当处于相同油膜厚度时,椭圆形液体润滑轴承承载能力会更大,可使用椭圆形液体润滑轴承代替圆形液体润滑轴承,提升轴承的安全系数;
(2)椭圆形轴承的椭圆度增加,使轴承的承载能力提升,同时油膜中心压力也在增加,因此必须考虑液体润滑轴承减摩材料的强度,避免使用椭圆轴承时,油膜中心压力增加导致减摩材料的失效;
(3)对使用椭圆形轴承的润滑油供油流量进行分析计算,为后续椭圆形轴承的使用提供理论指导。
(4)椭圆形液体润滑轴承在椭圆度的选型上应根据轧机的具体工况,在保证承载前提下,选择较低的椭圆度,因为随着轴承椭圆度的增加,会影响轧制板型的精度。
