双因素效应的动态二值logit模型的参数估计及应用

刘常彪，何庆光，王新军

（广西财经学院 中国-东盟统计学院，南宁 530007）

0 引言

带有不可观测个体效应（个体异质性）的面板数据离散选择模型在营销学、劳动者就业选择、出行方式选择等社会学领域有着广泛的应用。在这些领域的应用研究中发现，个体在做出选择决策时除了受个体效应的影响外，还会受到不可观测的时间效应（时间脉冲）的影响。在面板数据动态二值选择模型中考虑不可观测的个体效应和时间效应，可以使得模型更加灵活。在营销学的研究中，通常要考虑广告或优惠券的时效性、竞争商品价格随时间的变化，以及经济前景或天气随时间的变动,将这些影响因素称为时间脉冲或不可观测的时间效应。例如，公司在时变的市场条件下采用新技术，失业者随时间变化在外来劳动力市场冲击下找到工作等[1,2]。Chintagunta等（2005）[3]证明了在研究个体品牌选择时忽略时间效应会导致平均价格参数的估计是有偏的，同时夸大了个体之间对价格敏感参数异质性分布方差的估计，这将会影响管理层对定价和促销策略的决定。关于带有个体效应和时间效应的双因素面板数据模型的研究非常丰富，如，Hahn和Noon（2006）[4]研究了双因素面板数据AR（1）模型参数估计的偏差修正问 题；Kuksov 和Villas Boas（2008）[5]、Andrews 和Currim（2009）[6]、Draganska 和Klapper（2011）[7]使用双因素随机效应多项logit 选择模型来研究营销学中的品牌选择问题。最近，越来越多的文献使用双因素效应的线性回归模型来处理考虑个体效应和时间效应的问题[8—12]。

对于带有不可观测个体效应的面板数据动态二值模型,当个体维数较大、时间序列维数固定时，估计模型参数时会出现伴随参数问题，从而导致模型参数估计量不一致。Honore 和Kyriazidou（2000）[13]提出了用条件似然方法估计动态二值logit 模型参数；Bartolucci 和Nigro（2012）[14]、Bartolucci 等（2016）[15]分别提出了用拟条件似然方法和修正轮廓似然方法估计动态二值logit模型；Kitazawa（2022）[16]通过构造有效的矩条件提出一种方法估计动态logit模型；Gao 等（2017）[17]提出了一种方法消除个体效应，用来估计动态二值probit模型参数。尽管研究者们对带有个体效应的面板数据动态二值选择模型的参数估计和应用有了相当深入的研究，但对带有时间效应和个体效应的双因素面板二值选择logit 模型参数估计问题的研究还很少涉及。仅有Thomas（2006）[18]研究了带有个体效应和时间效应的双因素静态二值选择模型的参数估计问题，提出了用双重条件最大似然估计方法估计双因素静态二值logit 模型及半参数方法估计双因素静态二值选择模型。

本文提出了一个新的方法来估计带有个体效应和时间效应的双因素面板数据动态二值logit模型，该方法计算简单、快捷，不需要像Honore和Kyriazidou（2000）[13]的条件最大似然估计量那样构造核函数。同时，该方法也适用于静态二值logit 模型和带有个体效应的动态二值logit 模型。本文从理论上证明其优越性，并通过实证检验其应用价值。

1 模型与估计

1.1 双因素动态二值logit模型

考虑带有个体效应和时间效应的双因素动态二值logit模型：

其中，I(·)是示性函数；yit是可观测的因变量，如果潜变量y*it＞0，则yit=1，否则yit=0；αi表示不可观测的第i个个体效应；ξt表示t时刻固定的时间效应；εit为误差项；个体i和时间t相互独立，服从标准的logistic 分布；xit=(xi1，…，xiK)′是K×1 的协变量，协变量xit关于误差项εit是严格外生的；β是K×1 的偏好参数；γ是动态参数。本文的目的是在面板数据周期T固定的条件下估计模型结构参数θ=(β′，γ，ξ1，…，ξT)′。

在模型（1）中，考虑面板数据二值logit 模型的三种情形：第一，当ξt≡0，γ≡0（情形1）时，模型转化为面板数据静态二值logit 模型；第二，当ξt≡0（情形2）时，模型转化为带有个体效应的面板数据动态二值logit 模型；第三，考虑带有个体效应和时间效应（情形3）的双因素面板数据动态二值logit模型。

1.2 周期T=2 时模型的参数估计

不失一般性，先考虑T=2 时的模型参数估计问题。当T=2 时，模型（1）简化为如下形式：

在模型（2）中，为了得到模型参数θ=(β′，γ，ξ1，…ξ2)′的一致估计量，需要消除个体效应αi，给出如下假设：

假设1：设个体效应αi为随机的，与误差项εit（t=1，2）相互独立，且α1，…，αN之间独立同分布，其密度函数具有如下形式：

其中，g(·)是概率密度函数，其均值为0、方差为1；μα和σα是相应的位置参数和尺度参数。

记logistic 概率分布函数为L(x)=exp(x)/(1+exp(x))，误差项εi1、εi2相互独立且服从logistic 分布，其个体效应αi的密度函数为f(x)，则yi1，yi2的联合分布形式如下：

在某些情形下，个体之间的差异可能比较大，基于这种情形，考虑αi的分布是厚尾的，这意味着它的方差可以足够大。基于上面的方程式，当σα充分大时，给出如下两个引理。

引理1：在假设1满足的条件下，有：

证明：在假设1成立的条件下，有：

当M足够大时，对固定的ξ1、ξ2和xi1、xi2，L(-M-可以充分小。当M足够大时，积 分和∫t＜-M L(-t-ξ1-x′i1β)L(t+ξ2+x′i2β)dt也可以足够小。当σα足够大时，积分可以足够小。

因此，有：

引理1成立。

引理2：在假设1和引理1成立的条件下，有：

其中，G(x)=x/(ex-1)。在假设1成立的条件下，结合引理1，通过简单的计算可以得到上面的等式。

在假设1满足的条件下，应用引理2，可以得到如下条件概率：

基于式（4），模型参数θ的条件似然函数定义如下：

最大化上面的条件似然函数可以得到模型参数θ的估计量，即：

使用Newton-Raphson 迭代算法求解目标函数，可以得到参数的估计量。本文得出的估计量具有通常的统计性质：一致性和渐近正态性。下面的定理指出了模型参数估计量满足一致性和渐近正态性。

定理1：在假设1 满足且g(x) 可导的条件下，如果a＞0，则有：

（1）一致性：模型参数估计量一致收敛到真实参数θ，即当N→∞时，^→pθ。

（2）渐近正态性：模型参数估计量θ^ 满足渐近正态性，即kn(-θ)→LN(0，c∑-1，其中：

在定理1 中，→L表示依分布收敛，→p表示依概率收敛,在假设1 成立的条件下，推广Gao 等（2017）[17]论文中的定理1，可以得到该定理的证明。接下来，将提出的条件似然估计方法推广到T≥2 的情形下。

1.3 周期T ≥2 时模型的参数估计

记事件As={(yi1，…，yiT):yi1+…+yiT=s}，其中，s=0，1，…，T。定义条件选择概率函数如下：当s=0 时，有p(yi1，…，yiT|A0，xi1，…，xiT，θ}≡1；当s=T，有p(yi1，…，yiT|AT，xi1，…，xiT，θ}≡1。这意味着yit（t=1，…，T）取值全部为0 或1 时，不能为估计量提供有效的信息。当s=1，…，T-1时,有：

其中，ms为满足下面方程式的归一化常数：

利用引理2，经过简单的计算，可以得到如下的条件概率：

基于上式中的条件概率，最大化下面的条件似然函数得到模型参数θ的估计量：

使用Newton-Raphson迭代算法求解目标函数。

2 模拟研究

进行数值模拟研究旨在说明本文提出的估计量的有限样本性质。在模拟研究中考虑了三种不同的模型：（1）带有个体效应的静态二值logit模型，也就是ξt≡0，γ≡0；（2）带有个体效应的动态二值logit模型，也就是ξt≡0；（3）双因素动态二值logit模型。为了保持模拟框架的简洁性，在所有的模拟研究中假设协变量xit是一维的，每次模拟实验重复了500次，样本数量N≡200，500，1000，2000。

（1）先考虑T=2 时的静态二值logit模型，即yit=I{αi++εit＞0}，t=1，2。对不同的模型参数β=-0.5，0，0.5，将本文的估计量和Chamberlain（1980）[19]的条件最大似然估计量对比，结果显示在表1中。从表1中可以发现，随着样本容量N的增加，对不同的模型参数β，本文的估计量的偏差（Bais）和均方根误差（RMSE）都逐渐减小，对于较大的N，估计量的Bais接近于0，从模拟角度说明本文估计量一致收敛到真实的模型参数，模拟结果验证了定理1中一致性结论是成立的。根据模型参数估计量的Bais和RMSE发现，本文估计方法和条件最大似然估计方法的效果几乎是一样的。作为双因素动态二值logit模型参数估计方法的附属产品，可以认为本文的估计方法同样适用于静态logit模型，且该方法和条件最大似然估计方法相比同样有效。

表1 静态logit模型中，本文估计量 和条件最大似然估计量进行对比

表1 静态logit模型中，本文估计量 和条件最大似然估计量进行对比

注：T=2，重复500次，αi，xi1，xi2～N(0，π2/3)。

β N-0.5 0 0.5 RMSE(β^C)0.113 0.080 0.045 0.034 0.078 0.052 0.035 0.023 0.149 0.075 0.059 0.045 200 500 1000 2000 200 500 1000 2000 200 500 1000 2000 Bias(β^L)0.011 0.015 0.008 0.001 0.005 0.005 0.003 0.002 0.028 0.014 0.009 0.001 RMSE(β^L)0.118 0.079 0.049 0.038 0.100 0.051 0.044 0.022 0.150 0.090 0.048 0.039 Bias(β^C)0.009 0.014 0.003 0.001 0.006 0.003 0.003 0.001 0.028 0.012 0.008 0.001

（2）考虑带有个体效应的动态二值logit 模型，即yit=I将本文的估计方法和Honore 和Kyriazidou（2000）[13]的估计方法进行对比，结果见下页表2。可以发现，当T≤3 时，Honore 和Kyriazidou（2000）[13]的估计方法是无效的，因此，考虑T=4，将本文的估计方法和他们的方法进行模拟对比。在模拟设置中尽可能遵循Honore 和Kyriazidou（2000）[13]的 设 置，假 设 模 型 参 数β=1，γ=0.5，协变量xit（t=1，2，3，4）相互独立且服从N(0，π2/3)，个体效应模拟结果显示在表2 中。表2显示，本文的估计量有着更小的偏差和均方根误差，如：当样本容量N=200 时，本文的估计量与真实值的偏差为0.018，均方根误差为0.101，相应的Honore 和Kyriazidou（2000）[13]的估计量的偏差为0.128，均方根误差为0.303。从估计量的偏差和均方根误差来看，显然本文的估计方法具有明显的优势。

表2 动态logit模型中，本文估计量、 和文献[3]的估计量,进行对比

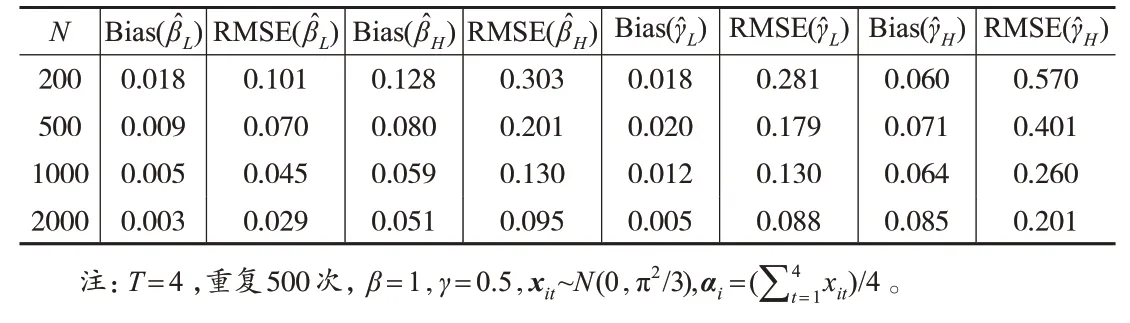
表2 动态logit模型中，本文估计量、 和文献[3]的估计量,进行对比

N 200 500 1000 2000 Bias(β^L)0.018 0.009 0.005 0.003 RMSE(β^L)0.101 0.070 0.045 0.029 Bias(β^H)0.128 0.080 0.059 0.051 RMSE(β^H)0.303 0.201 0.130 0.095 RMSE(γ^ H)0.570 0.401 0.260 0.201注：T=4，重复500次，β=1，γ=0.5，xit～N(0，π2/3),αi=(∑t4= 1xit)/4。Bias(γ^ L)0.018 0.020 0.012 0.005 RMSE(γ^ L)0.281 0.179 0.130 0.088 Bias(γ^ H)0.060 0.071 0.064 0.085

（3）考虑双因素动态二值logit 模型，即yit=I{αi+ξt++γyit-1+εit＞0}。不失一般性，在模拟设置中，将ξ1=0作为对照，周期T=3，模型参数β=1，γ=0.5，ξ2=0.4，ξ3= 0.2 ，协 变 量xit(t=1，2，3) 相 互 独 立 且 服 从N(0，π2/3)，针对个体效应不同分布来检验本文估计量的有效性，模拟结果显示在表3 中。与预期一致，对个体效应的不同分布，估计量的偏差随着样本容量的增加逐渐趋近于0，均方根误差也逐渐减小，模拟结果显示本文的估计方法对双因素动态二值logit模型也是有效的。

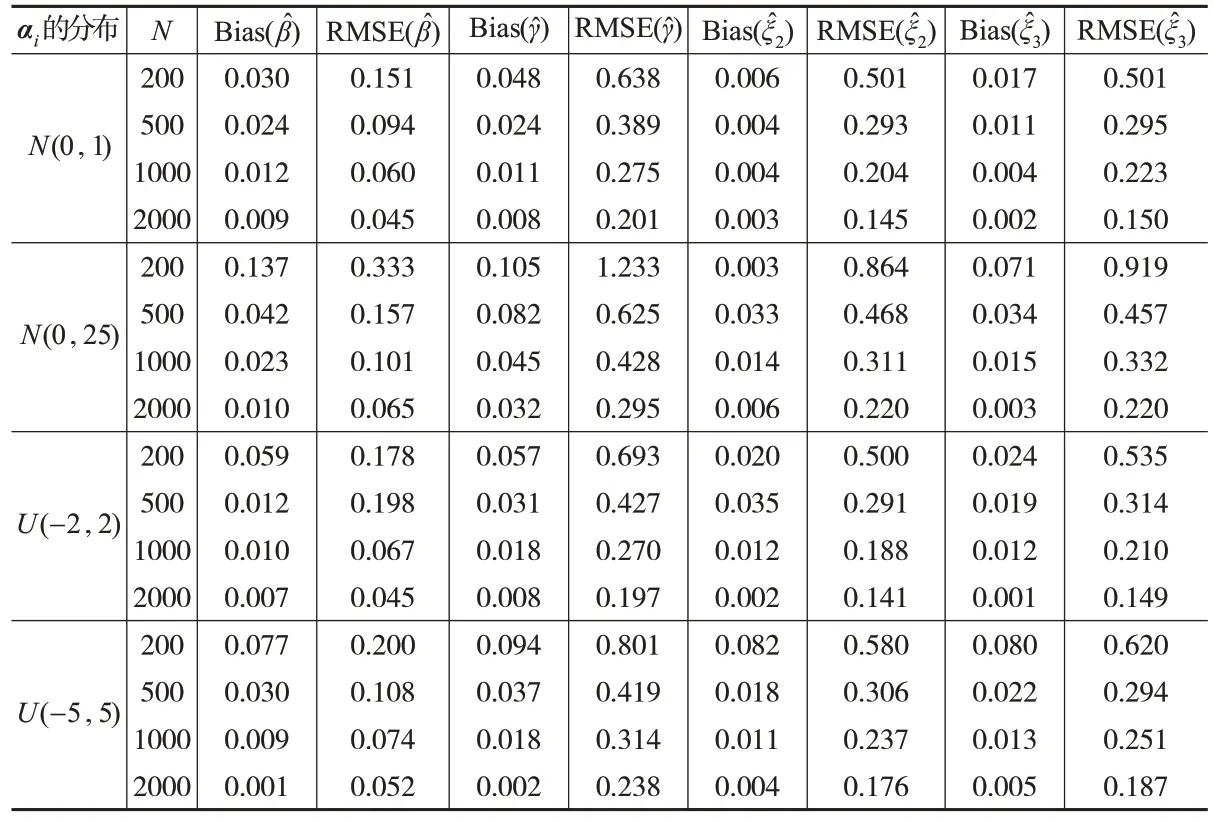
表3 双因素动态二值logit模型中，对αi 的不同分布模拟本文估计量

3 实证分析

通过实证分析来检验本文所提方法的应用价值。为了在实证分析中检验滞后因变量yit-1是否对当前因变量yit有着显著的影响，考虑A.C.Neilsen 收集的洗涤用品购买数据，数据可以在JAE 数据库中获得。在实际分析中，本文选择了洗涤品牌“Tide”,相对于其他品牌，它的市场占有率为36.13%，具有最高的市场份额。本文考虑了至少连续三次选择品牌“Tide”的个体，且保留数据的前三个周期用于分析，得到共467个个体的购买数据。在分析的数据中，三个购买周期的价格变量相差很小，因此本文忽略了该变量，选择滞后的因变量作为解释变量估计模型参数。

表4中展示了467个个体在三个周期内选择购买品牌“Tide”洗涤剂的相关数据。yit=1（t=1， 2， 3）表示第t个周期第i个个体购买了“Tide”洗涤剂；yit=0 表示第t个周期个体i没有购买“Tide”洗涤剂。如果连续两个或三个周期内都有yit=1 或yit=0，就意味着消费者在这些周期内全部购买了该品牌或没有购买该品牌，说明在品牌选择中消费者表现出一定的惯性或持续性，也就是上次的购买决策影响了个体下一次的购买意愿。从表4中可以看出，连续三个周期全部购买该品牌或没购买该品牌的个体数量占总数量的73.01%，这说明在消费者选择时表现出较强的购买惯性。根据表4中的数据，使用本文提出的估计方法得到模型参数γ的估计值和标准差分别为=0.356，=0.198,动态参数γ的估计值为正，显示模型中滞后因变量yit-1与当前因变量yit存在动态关系，也表明消费者在购买时表现出一定的持续性，即前一个周期购买了“Tide”洗涤剂将会增加下一个周期选择品牌“Tide”的概率。时间效应参数的估计值和标准差分别为=0.307,=0.184和=0.171,=0.156，估计结果显示，消费者在品牌购买时受到了时间脉冲的影响，且随着时间的延长，时间脉冲的影响会逐渐降低。

表4 三个周期的购买数据

4 结束语

本文研究了双因素面板数据动态二值logit模型的参数估计问题，基于条件似然的思想提出了一种新的估计方法并给出估计量的渐近性质。提出的估计方法适用于静态二值logit模型、动态二值logit 模型及双因素动态二值logit 模型。模拟仿真结果表明，在静态logit 模型中，本文的估计方法和Chamberlain（1980）[19]的条件最大似然方法表现一样好；但在动态logit模型中，本文的估计方法远远优于Honore 和Kyriazidou（2000）[13]的估计方法，是一种更有效的估计量。本文的估计方法也可以推广到双因素面板数据动态probit模型中，而不只是局限于二值logit模型的框架内。