城市数字经济发展水平的分布动态、地区差异与收敛性研究

侯 杰，李卫东，张杰斐，刘文杰

（1.巢湖学院 经济与法学学院，合肥 238024；2.北京交通大学 经济管理学院，北京 100044；3.中国工业互联网研究院，北京 100102）

0 引言

近年来，数字经济在国民经济中的地位更加稳固、支撑作用更加明显。然而，我国数字经济的发展水平具有明显的区域差异和空间梯度。国家中心城市和省会城市率先颁布政策，积极规划数字经济发展格局，抢占数字经济发展先机，从而引领并带动区域性数字经济发展。

既有文献大多是从省域层面对数字经济发展水平的分布动态、地区差异和收敛性展开分析。焦勇（2021）[1]采用核密度估计法和Dagum 基尼系数及其分解法，分析了2014—2018 年我国八大综合经济区数字经济发展水平的地区差异和动态演进特征，得出八大综合经济区的数字经济发展水平差异显著的结论。潘为华等（2021）[2]采用核密度估计法和空间计量模型，分析了2012—2019年我国31个省份数字经济发展水平的时空演化和动态分布特征，发现我国省域数字经济发展水平不断提高，但存在明显的发展梯度，空间上具有正向依赖、空间集聚和相对稳定的特征。何苗和任保平（2022）[3]采用核密度估计法、Dagum基尼系数及其分解法和空间计量模型，分析了2016—2020年我国31个省份数字经济发展水平的变化趋势及收敛性，发现我国省域数字经济发展水平稳步提升，但存在明显的发展梯度，省份间的绝对差距扩大、相对差距缩小，数字经济发展水平存在显著的σ收敛和β收敛。

已有研究从省域层面揭示了数字经济发展水平的分布动态、地区差异和收敛性，大多得出了数字经济发展水平稳步提升但存在较大的区域差距，以及区域数字经济发展水平具有一定的收敛性的结论。然而，从省域层面分析数字经济发展水平的视角过于宏观，在一定程度掩盖了省域内部城市之间的数字经济发展水平不平衡的问题。现实中，数字经济的萌芽、发展与壮大往往先出现在城市层面而非省域层面，只有城市层面得到发展才能影响到省域层面。因此，本文将研究视角定位于城市，探讨我国城市数字经济发展的分布动态、地区差异和收敛性。

1 研究设计

1.1 评价指标体系构建

本文主要借鉴黄慧群等（2019）[4]、刘军等（2020）[5]和赵涛等（2020）[6]的思路，构建的数字经济发展水平的评价指标体系如表1所示。进而采用熵权法进行测度，计算得出数字经济发展水平。

表1 数字经济发展水平的评价指标体系

1.2 研究方法

1.2.1 核密度估计法

核密度估计是一种测算连续型随机变量概率密度函数的方法。该方法采用光滑的峰值函数拟合所需测度的样本数据，并利用连续的密度曲线描绘出随机变量的分布形态。其假定随机变量X的概率密度函数为：

其中，n表示样本容量；xi表示从总体X中抽取的独立同分布样本的观测值；xˉ表示样本均值；K(·)表示核函数，本文选择高斯核函数进行估计；b表示带宽，是一个预先给定的正数。采用核密度估计法得到的曲线图像可以反映研究对象的分布位置、分布形态、延展性和极化现象四大特征。

1.2.2 Dagum基尼系数及其分解方法

Dagum基尼系数是对传统基尼系数的升级，能够完整地展示区域差异和贡献率，常被用于分析区域差异的主要来源[7]。根据Dagum（1997）[8]提出的基尼系数及其分解方法，基尼系数G的计算公式如下：

式（2）中，i和h表示不同区域，j和r表示不同城市，n为城市总数，k为区域总数。

进一步地，区域i的基尼系数Gii和区域内差异Gw、区域i和h之间的基尼系数Giℎ、区域间净值差异Gnb、超变密度Gt的计算公式依次如下：

1.2.3 收敛模型

收敛模型可以用于分析经济活动是否存在新古典增长模型所预言的“稳态”和“收敛”两种特性，主要包括σ收敛、β收敛等形式。

σ收敛是指不同组别的城市数字经济发展水平偏离平均水平的幅度逐渐减小。本文采用变异系数[9]进行σ收敛检验，计算公式如下：

其中，Digei,j表示i组别j城市的数字经济发展水平表示i组别j城市数字经济发展水平的均值，Nj表示各个组别的城市数量。若σ值随着时间的推移逐渐减小，则说明存在σ收敛。

β收敛模型可以分为绝对β收敛模型和条件β收敛模型。其中，绝对β收敛模型不考虑其他外部因素。参考Barro（1991）[10]所提出的模型，本文设定绝对β收敛模型的具体形式如下：

式（13）中，T表示考查时间段。

条件β收敛模型考虑了其他因素对数字经济发展水平的影响，因此在构建模型时需要添加若干个控制变量，其具体形式如下：

式（14）中，Xit表示控制变量。本文选取的控制变量包括：经济增长水平（Pgdp），采用人均GDP 进行衡量；产业结构（Stru），采用第三产业产值占GDP 的比重进行衡量；政府干预程度（Gov），采用地方政府财政预算支出与GDP的比值进行衡量。本文的研究对象为285个城市，并依据2014 年国务院印发的《关于调整城市规模划分标准的通知》，将285 个城市划分为超大和特大城市、大城市、中小城市三个规模等级城市组别。本文研究的时间跨度为2011—2020 年，所使用的数据全部来自2012—2021 年《中国城市统计年鉴》以及由北京大学数字金融研究中心联合蚂蚁金服集团共同编制的北京大学数字普惠金融指数，个别缺失的数据采用插值法进行补充。各变量的描述性统计如表2所示。

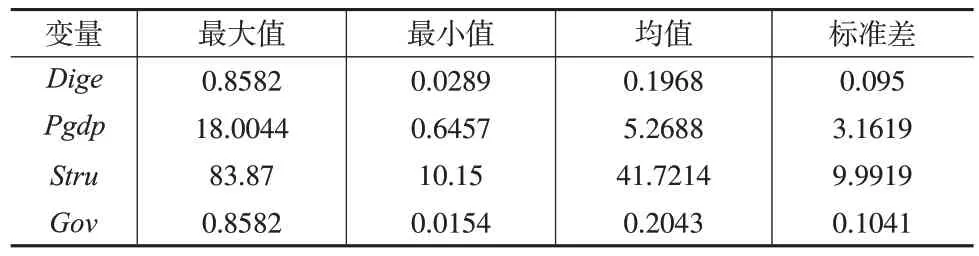
表2 描述性统计

2 数字经济发展水平的分布动态

为了考查全国和不同规模等级城市的数字经济发展水平的绝对差异的动态特征，本文运用核密度估计法得到核密度图。图1 依次展示了全国、超大和特大城市、大城市、中小城市四组样本的数字经济发展水平的分布位置、分布形态、延展性和极化现象。

图1 不同组别的数字经济发展水平的分布动态

由图1（a）可知全国数字经济发展水平的动态演进过程。从分布位置来看，分布曲线中心及其变化区间逐渐右移，移动速度放缓，反映了全国数字经济发展水平逐渐上升但增速放缓。从分布形态来看，主峰高度呈现逐渐下降的趋势，分布曲线的宽度逐渐拓宽，反映了全国数字经济发展水平的绝对差异变大。从延展性来看，分布曲线存在右拖尾现象且逐渐显现，反映了全国数字经济发展水平的差距逐渐扩大。从极化现象来看，分布曲线呈现单峰形态，不存在两极或多极化趋势。综合来看，全国数字经济发展水平的分布曲线呈现逐渐右移、高度下降、宽度扩大、右拖尾显现的形态特征，反映了全国数字经济发展水平整体上稳步提升，但城市之间的绝对差异变大且差距扩大的现象。

由图1（b）可知超大和特大城市数字经济发展水平的动态演进过程。从分布位置来看，分布曲线中心及其变化区间逐渐右移，移动速度放缓，反映了超大和特大城市的数字经济发展水平逐渐上升但增速放缓。从分布形态来看，主峰高度呈现逐渐下降的趋势，且曲线宽度逐年拓宽，反映了超大和特大城市的数字经济发展水平的绝对差异变大。从延展性来看，分布曲线右拖尾现象逐渐显现，反映了超大和特大城市的数字经济发展水平的差距逐渐扩大。从极化现象来看，分布曲线由起初的单峰形态发展为“一主一侧”的双峰形态，但侧峰相较主峰并不明显，与主峰差异不大；并且2018年以后，侧峰的高度大幅下降。这反映了超大和特大城市的数字经济发展水平出现两极分化现象，但这种现象逐渐弱化。综合来看，超大和特大城市的数字经济发展水平的分布曲线呈现逐渐右移、高度下降、宽度扩大、右拖尾显现、多峰的形态特征，反映了超大和特大城市的数字经济发展水平整体上稳步提升，但城市之间的数字经济发展水平的绝对差异变大且差距扩大，存在两极化现象。

由图1（c）可知大城市数字经济发展水平的动态演进过程。从分布位置来看，分布曲线中心及其变化区间逐渐右移，移动速度放缓，反映了大城市的数字经济发展水平逐渐上升但增速放缓。从分布形态来看，主峰高度呈现逐渐下降的趋势，分布曲线的宽度逐渐拓宽，反映了大城市的数字经济发展水平的绝对差异变大。从延展性来看，分布曲线右拖尾现象逐渐显现，反映了大城市的数字经济发展水平的差距逐渐扩大。从极化现象来看，分布曲线总体呈现单峰形态。综合来看，大城市的数字经济发展水平的分布曲线呈现逐渐右移、高度下降、宽度扩大、右拖尾显现的形态特征，反映了大城市的数字经济发展水平整体上稳步提升，但城市之间的数字经济发展水平的绝对差异变大且差距扩大的现象。

由图1（d）可知中小城市数字经济发展水平的动态演进过程。从分布位置来看，分布曲线中心及其变化区间逐渐右移，移动速度放缓，反映了中小城市的数字经济发展水平逐年上升但增速放缓。从分布形态来看，主峰高度呈现逐渐下降的趋势，分布曲线的宽度略微拓宽，反映了中小城市的数字经济发展水平的绝对差异小幅度变大。从延展性来看，分布曲线右拖尾现象有所改善，反映了中小城市的数字经济发展水平的差距在缩小。从极化现象来看，分布曲线由起初的单峰状态逐步转变为“一主一侧”的双峰形态，反映了中小城市的数字经济发展水平出现两极分化。综合来看，中小城市的数字经济发展水平的分布曲线呈现逐渐右移、高度下降、宽度扩大、右拖尾弱化、多峰的形态特征，反映了中小城市的数字经济发展水平整体上稳步提升，城市之间的数字经济发展水平的绝对差异变大但差距缩小，存在两极分化现象。

3 数字经济发展水平的空间差异及其来源

为了进一步揭示全国和不同规模等级城市的数字经济发展水平的空间差异及其来源，本文采用Dagum基尼系数及分解方法进行测算与分析。

3.1 全国和区域内差异

全国和不同规模等级城市内部的数字经济发展水平的基尼系数值及其变化趋势如图2所示。

图2 全国和区域内基尼系数值及其变化趋势

由图2 可知全国和区域内数字经济发展水平的基尼系数值及其变化趋势。全国和区域内基尼系数值均呈现缓慢下降的趋势，反映了全国和区域内的数字经济发展水平的空间差异逐渐缩小。其中，全国、大城市和中小城市的基尼系数值的变化趋势相似，大体都经历了“大幅下降—趋缓下降—大致平稳”三个阶段，2011—2016年大幅下降，2016—2018年趋缓下降，2018—2020年大致平稳。从具体的基尼系数值及其下降幅度来看，全国的基尼系数值在2011 年最高，为0.26，到2020 年下降至0.17，降幅达到了34.62%。大城市的基尼系数值在2011年最高，为0.23，到2020 年下降至0.14，降幅达到了39.13%。中小城市的基尼系数值在2011年最高，为0.17，到2020年下降至0.10，降幅达到了41.18%。而超大和特大城市的基尼系数值虽总体呈现下降趋势，但下降幅度相较于全国和其他规模等级城市要小一些。超大和特大城市的基尼系数值经历了“趋缓下降—小幅回升—大致平稳”三个阶段，2011—2017年小幅下降，2017—2018年小幅上升，2018—2020年趋于平稳。从具体的基尼系数值及其下降幅度来看，超大和特大城市的基尼系数值由2011年最高为0.21下降至2020年的0.17，降幅达到了19.05%。由此可见，近年来，超大和特大城市的基尼系数值最大，反映了超大和特大城市内部的数字经济发展水平的差距最为显著，其次是大城市，中小城市内部的数字经济发展水平的差距最小。中小城市的基尼系数值降幅最大，大城市的基尼系数值降幅次之，超大和特大城市的基尼系数值降幅最小。

3.2 区域间差异

不同规模等级城市之间的数字经济发展水平的基尼系数值及其变化趋势如图3所示。

图3 区域间基尼系数值及其变化趋势

由图3 可知区域间数字经济发展水平的基尼系数值及其变化趋势。从区域间基尼系数值来看，超大和特大城市-中小城市的基尼系数值最大，超大和特大城市-大城市的基尼系数值次之，大城市-中小城市的基尼系数值最小，这反映了超大和特大城市-中小城市之间的数字经济发展水平差距最大，超大和特大城市-大城市之间的数字经济发展水平差距次之，大城市-中小城市之间的数字经济发展水平差距最小。这符合产业发展的区域梯度规律，由于不同规模等级城市发展数字经济的自然禀赋、经济能力、技术水平、市场环境等因素存在客观差异，因此不同规模等级城市之间的数字经济发展水平存在明显差距。城市规模越大，培育数字经济的要素越丰富，发展数字经济的能力就越强。超大和特大城市的数字经济发展水平最高、大城市次之，中小城市最低，这就造成了超大和特大城市-中小城市之间的数字经济发展水平差距最大。从区域间基尼系数值的变化趋势来看，区域间基尼系数值大体呈现下降的趋势，反映了区域间数字经济发展水平的差距逐渐缩小。其中，超大和特大城市-中小城市与超大和特大城市-大城市的区域间基尼系数值的变化趋势相似，大体经历了“大幅下降—小幅回升—趋缓下降”三个阶段，2011—2012 年大幅下降，2012—2013 年小幅回升，2013—2020年趋缓下降。从具体的基尼系数值及其下降幅度来看，超大和特大城市-中小城市的基尼系数值由2011年最高为0.44 下降至2020 年的0.33，降幅达到了25.00%。超大和特大城市-大城市的基尼系数值由2011 年最高为0.38下降至2020年的0.29，降幅达到了23.68%。大城市-中小城市的基尼系数值由2011年最高为0.21下降至2020年的0.13，降幅达到了14.29%。由此可见，超大和特大城市-中小城市的基尼系数值降幅最大，超大和特大-大城市的基尼系数值降幅次之，大城市-中小城市的基尼系数值降幅最小。

3.3 差异来源和贡献率

不同规模等级城市的数字经济发展水平的区域差异来源和贡献率及其变化趋势如图4所示。

图4 数字经济发展水平的区域差异来源和贡献率

由图4 可知数字经济发展水平区域差异的来源和贡献率及其变化趋势。从差异来源的贡献率具体数值来看，区域间差异的贡献率持续高于区域内差异和超变密度的贡献率，区域间差异的贡献率常年保持在50%以上，区域内差异的贡献率的浮动范围介于29.90%～32.41%，超变密度的贡献率的浮动范围介于14.07%～16.97%。三者贡献率的均值分别为53.62%、30.97%和15.41%。由此可见，造成数字经济发展水平存在区域差异的第一来源是区域间差异，第二来源是区域内差异，第三来源是超变密度。从差异来源的变化趋势来看，区域间差异的贡献率总体呈现小幅上升的趋势，贡献率由2011 年的50.82%上升至2020 年的53.97%，升幅达到了6.20%。区域内差异的贡献率总体呈现不规则的波动趋势，但波动幅度较小，贡献率由2011年的32.21%下降至2020年的30.71%，降幅达到了4.67%。超变密度的贡献率总体呈现不规则的波动趋势，但波动幅度较小，贡献率由2011年的16.97%下降至2020 年的15.32%，降幅达到了9.72%。由此可见，区域间差异的贡献率整体上升，而区域内差异和超变密度的贡献率整体下降；超变密度的贡献率的变化幅度最大，其次是区域间差异的贡献率，区域内差异的贡献率的变化幅度最小。

4 数字经济发展水平的收敛性分析

4.1 σ 收敛检验与结果分析

为量化全国和不同规模等级城市的数字经济发展水平的收敛趋势，本文采用变异系数测度σ收敛，结果如图5所示。

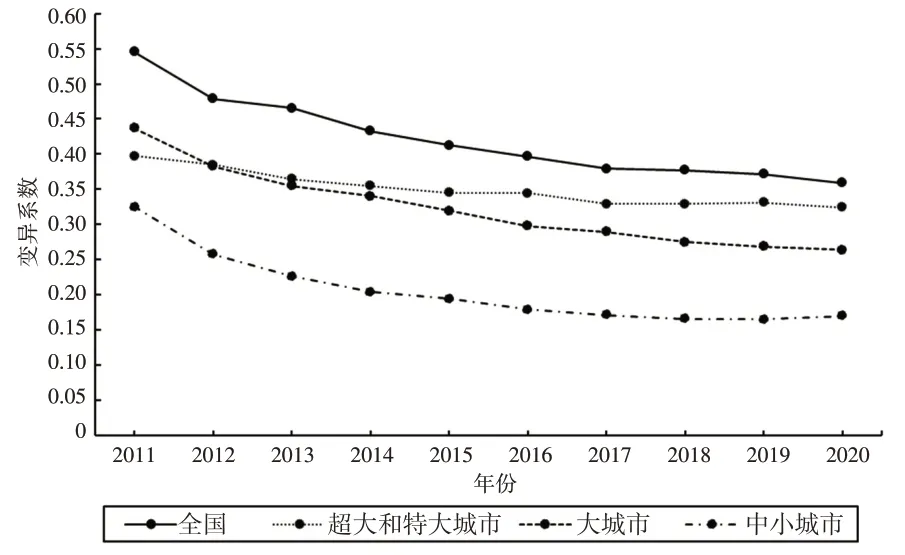
图5 不同组别样本的数字经济发展水平的变异系数及其变化趋势

由图5 可知全国和不同规模等级城市的数字经济发展水平的变异系数及其变化趋势。全国和不同规模等级城市的数字经济发展水平的变异系数均呈现逐渐下降的趋势，反映了全国和不同规模等级城市的数字经济发展水平存在σ收敛。其中，全国、大城市和中小城市的数字经济发展水平的变异系数的变化趋势相似，变异系数的下降趋势明显。全国的变异系数由2011年最高为0.55下降至2020 年的0.36，降幅达到了34.55%。大城市的变异系数由2011 年最高为0.44 下降至2020 年的0.26，降幅达到了40.9%。中小城市的变异系数由2011 年最高为0.33 下降至2020年的0.17，降幅达到了48.48%，而超大和特大城市的变异系数虽总体上呈现下降趋势，但下降幅度相较于全国和其他规模等级城市要小很多。超大和特大城市的变异系数由2011 年最高为0.40 下降至2020 年的0.32，降幅达到了20%。由此可见，中小城市的变异系数的降幅最大，反映了中小城市的数字经济发展水平的σ收敛幅度最大；大城市的变异系数的降幅次之；超大和特大城市的变异系数的降幅最小，反映了超大和特大城市的数字经济发展水平的σ收敛幅度最小。

4.2 β 收敛检验与结果分析

鉴于不同规模等级城市的空间布局较为分散，经济活动的空间关联性较弱，为了更好地进行不同规模等级城市的数字经济发展水平的收敛性的横向对比，本文构建了普通面板回归模型，以检验全国和不同规模等级城市数字经济发展水平的β收敛趋势。其中，全国和不同规模等级城市的数字经济发展水平的绝对β收敛的回归结果如表3所示。

由表3 可知全国和不同规模等级城市的数字经济发展水平的绝对β收敛的回归结果。从收敛系数的正负和显著性来看，全国和不同规模等级城市的绝对收敛的β值均为负，并在1%的水平下通过了显著性检验，表明了全国和不同规模等级城市的数字经济发展水平存在绝对β收敛。基于收敛系数β可以计算出收敛速度v，从收敛速度来看，中小城市的绝对收敛速度最大，为0.0242；其次是超大和特大城市，为0.0234；大城市的绝对收敛速度最小，为0.022。

全国和不同规模等级城市的数字经济发展水平的条件β收敛的回归结果如表4所示。

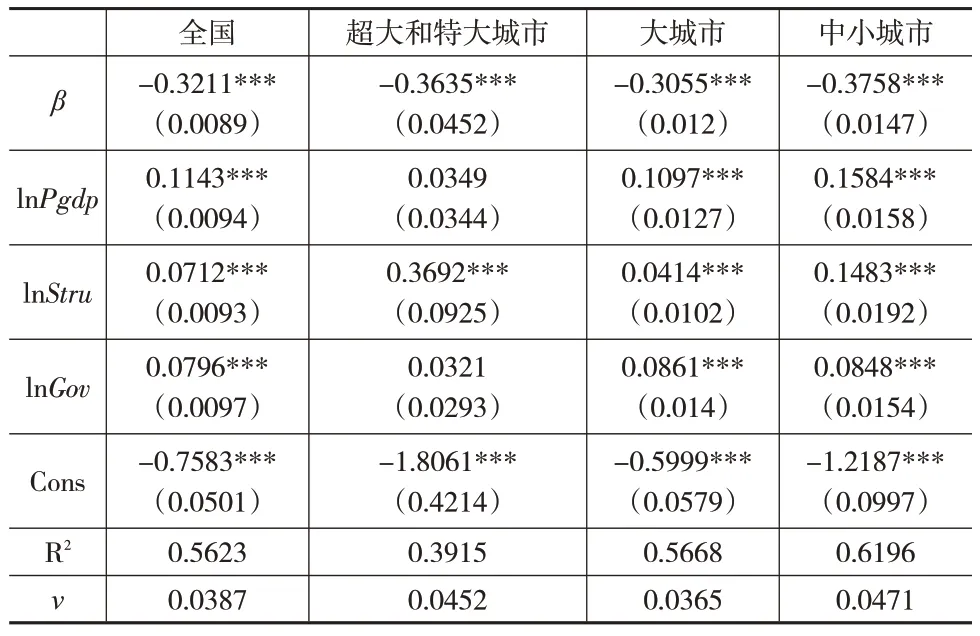
表4 不同组别样本的数字经济发展水平的条件β 收敛的回归结果

由表4 可知全国和不同规模等级城市的数字经济发展水平的条件β收敛的回归结果。从收敛系数的正负和显著性来看，全国和不同规模等级城市的条件收敛的β值均为负，并在1%的水平下通过了显著性检验，表明了全国和不同规模等级城市的数字经济发展水平存在条件β收敛。基于收敛系数β可以计算出收敛速度v，从收敛速度来看，中小城市的条件收敛速度最大，为0.0471；其次是超大和特大城市，为0.0452；大城市的条件收敛速度最小，为0.0365。与绝对β收敛的结果相比较可以看出，控制变量所代表的因素推动全国和不同规模等级城市的数字经济发展水平趋于加速收敛[12]。

5 结论

本文基于2011—2020年我国285个城市的面板数据，划分了超大和特大城市、大城市、中小城市三种不同规模等级城市组别，运用核密度估计、Dagum基尼系数、收敛模型分析了我国城市数字经济发展水平的分布动态、地区差异与收敛性。研究结论如下：（1）核密度估计结果反映了全国和不同规模等级城市的数字经济发展水平呈现稳步上升趋势，但城市之间数字经济发展水平的绝对差异有所扩大。（2）区域内基尼系数值及其变化趋势反映了超大和特大城市内部的数字经济发展水平的差距最为显著，其次是大城市，最后是中小城市。（3）区域间基尼系数值及其变化趋势反映了超大和特大城市-中小城市之间的数字经济发展水平差距最大，其次是超大和特大城市-大城市，最后是大城市-中小城市。（4）差异来源和贡献率及其变化趋势反映了造成数字经济发展水平存在区域差异的第一来源是区域间差异，第二来源是区域内差异，第三来源是超变密度。（5）收敛性分析结果反映了全国和不同规模等级城市的数字经济发展水平存在σ 收敛和β 收敛，β 收敛速度由大到小依次为中小城市、超大和特大城市、大城市。