截击型无人机多目标气动外形优化设计

杨德敏　林三春　李易

摘要：使用无人机碰撞拦截无人机是一种有效且成本适中的反制手段。 为提高优化设计效率， 本文采用雷诺平均Navier-Stokes方程计算流场， 并使用Kriging代理模型和基于分解的多目标进化算法（MOEA/D）针对鸭式布局截击型无人机开展气动外形优化设计。 设计过程中， 以航程和最大可用过载为设计目标， 将鸭翼纵向位置、 主翼扭转角、 展弦比和后掠角作为设计变量， 以静稳定度和鸭翼最大偏转角为约束， 得到了分布均匀的Pareto前沿， 优化后的无人机航程与最大可用过载较基准外形分别提升了24.6%和6.4%， 证明了该优化方法的有效性。

关键词：反无人机； 鸭式布局； Kriging代理模型； MOEA/D； 多目标优化

中图分类号： V221+.3文献标识码：A文章编号： 1673-5048（2023）03-0074-06

DOI： 10.12132/ISSN.1673-5048.2022.0121

0引言

近年来， 各类小型侦察无人机和察打一体无人机在如叙利亚内战、 纳卡战争等地区武装冲突和局部战争中被大量使用［1］，  其体积小、 难探测， 给阵地防空和后勤运输造成了巨大威胁。 当拦截中距离（约5～50 km）小型无人机时， 自动化高炮与电磁武器的射程不足［2］， 中远程防空导弹的成本较高， 截击型无人机便成为当前技术条件下一种成本适中的、 有效的、 能弥补末端近防武器和远程防空导弹防御漏洞的拦截手段［3］。 该类型无人机发射后会先飞行至任务空域， 然后根据自身导引头提供的测量信息导引无人机接近目标并引爆战斗部以摧毁目标［4］。 该方法相对近防炮和中近程防空导弹， 成本更低且毁伤概率大。 2021年， 美国陆军将雷神公司“郊狼”无人机作为近程反无人机方案， 该无人机配备有雷达导引头和战斗部， 可以有效识别和毁伤目标无人机［5］。

高显忠等［6］分析了无人机蜂群攻击模式， 提出截击型无人机应当成为中近程拦截的重要手段， 以直接碰撞的形式实现有效毁伤。 周洲等［7］建立了自主拦截无人机的作战效能模型， 并分析导引头视场角、 突防距离等影响因素， 给出了任务指标分配建议。 以上研究分析了截击型无人机的重要性与作战效能， 但总体方案和气动外形设计等更深入的研究方面， 未见报道。

截击型无人机的作战模式要求其同时具有大航程和大机动过载， 这两个设计目标有时是相互约束与冲突的。 对于多目标设计问题， 传统依靠经验的“试凑法”设计成本高、 周期长， 且难以得到最优的气动外形。 进化算法虽然具有较好的全局性， 但会大量调用CFD计算， 导致计算成本过高。 近年来， 代理优化算法在气动外形设计领域得到了大量的应用。 韩忠华等［8］针对大型民机机翼采用Kriging代理模型开展多轮优化设计， 获得了满足设计要求的气动外形， 验证了该方法的有效性和工程实用性。 进一步， 当采用多目标进化算法时， 代理优化算法可以很好地解决多目标气动优化问题。 曹粟等［9］以飞行器航程、 总热流量和飞行时间为优化目标， 采用基于分解的多目标进化算法［10］（MOEA/D）得到三锥体临近空间拦截器的Pareto前沿， 证明了该算法的优势和可行性。 文献［11-12］也证明了MOEA/D在处理复杂非线性多目标问题的优势与巨大应用潜力。

本文将代理模型和MOEA/D算法应用于截击型无人机的多目标气动优化设计， 以航程和最大可用过载为设计目标，  通过分析Pareto优化前沿，  得到设计变量对目标特性的影响， 给出截击型无人机外形的设计建议。

1优化问题描述

1.1基准模型

根据截击型无人机的典型作战模式， 可知其主要追求大航程和末段可用过载， 对应的气动参数为巡航升阻比和最大升力系数。 鸭式布局飞行器巡航飞行时， 配平阻力小、 升阻比大。 同时鸭翼位于机翼之前， 操纵效率高， 提高了鸭式布局无人机的操纵性和机动性［13］。 因此， 本文无人机基准外形选择鸭式布局， 如图1所示， 同時采用尾推式电动螺旋桨驱动， 可忽略其对气动特性的影响。 鸭翼纵向位置距头部50 mm， 垂向位置距参考平面20 mm， 展弦比为5。 主机翼纵向位置距头部450 mm， 展弦比为7， 扭转角为-4°。

1.2优化目标

4优化设计结果

4.1优化前沿分析

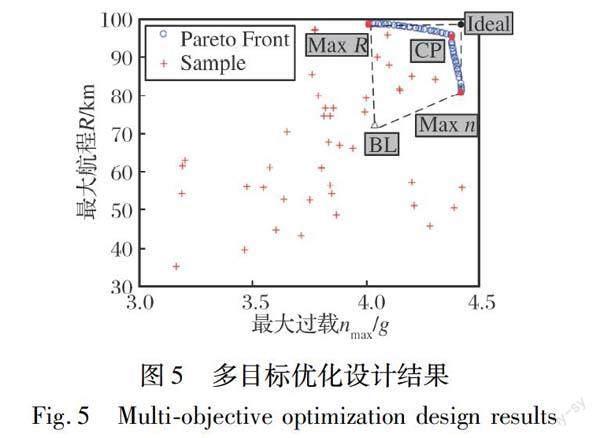
图5给出了多目标优化设计的结果， 其中空心圆圈代表优化后的前沿点， 其均匀分布在曲线上， 不同的位置体现了两个优化目标的冲突与妥协。 红色“+”标记点表示用于构建代理模型的样本点集， 其中包括30个初始样本点和3次迭代过程中添加的12个样本点， 其较为均匀地随机分布在样本空间中， 侧面证明了该代理模型具有较好的全局性。

在Pareto前沿的两端， 两个红色实心圆分别代表以航程R和最大过载nmax为目标的单目标优化结果， 分别标记为Max R和Max n， 其代表了在满足约束的前提下， 两个子目标所能达到的最优值。 而从Max R和Max n位置引出的虚线交于点Ideal， 表示“最大理想状态”。 但是由于优化子目标之间相互冲突， 该理想状态是达不到的。 在Pareto前沿的中心取一折中点CP（Compromise Point）， 表示了对于两个目标的折中。

图中黑色三角形给出基准外形BL（BaseLine）对应的目标性能， 很明显， 基准外形离Pareto前沿还有相当的距离， 这说明基准外形有较大的可优化空间。 从基准外形点引出的虚线与Pareto前沿构成了多边形， 在该多边形区域内的所有点， 均比基准外形点的性能要优异。

Pareto前沿比较短， 是因为两个优化目标并非绝对的冲突。 从式（2）～（4）可以发现， 优化目标取决于巡航升阻比、 最大升力系数和无人机质量。 巡航升阻比和最大升力系数存在一致性， 即当展弦比增大、 后掠角减小时， 巡航升阻比和最大升力系数同时增大， 但与此同时， 无人机重量W也会跟着增大。 因而， 由于冲突因素， 即变量W的加入， 使得两个优化目标存在一定的冲突性。 目标的一致性使得优化前沿集中在图片的右上角， 而目标的冲突性使得优化前沿弯曲成图中的形状。

为了验证代理模型的精度和优化过程的有效性， 从Pareto前沿选取3个典型外形进行CFD分析， 在表2中给出了验证结果。 结果表明代理模型计算结果与CFD计算结果一致性较好， 最大误差不超过2.5%。 此处只说明代理模型对CFD数据集的拟合效果较好， 并不讨论CFD结果本身的精度。

图6给出了设计变量在Pareto前沿的取值， X轴代表设计变量的维度。 图中显示鸭翼纵向位置xc取值范围在7～12 mm之间， 表明鸭翼位置为了实现纵向配平而做出的调整； 机翼扭转角θ取值范围在-3°～ 0°之间， 说明机翼扭转角并非越大越好； 机翼展弦比AW取值范围在5～8之间， 说明展弦比过大会对机翼质量造成较大的负担， 导致整机性能下降； 机翼后掠角Λ在4°～ 6°之间取值， 既保证了稳定性又不致于机翼质量太大。

4.2典型外形分析

为了深入研究优化前沿上设计外形性能优良的原因， 选取前沿上基准点BL、 最大航程点Max R、 最大过载点Max n和折中点CP四个典型外形， 对比研究其几何外形特点和飞行性能。 表3给出了折中点CP与基准点BL的外形及性能参数。 与基准点BL相比， 折中点CP的展弦比和后掠角均有所减小， 这可以减轻无人机质量。 同时， 减小扭转和后掠角可以分别提高巡航升阻比和最大升力系数， 有利于全机性能的提升。 最终， 折中点无人机的航程增加24.6%， 最大过载增加6.4%。 为了表现子目标之间的冲突与协调对设计变量的影响， 图7给出四个典型外形的二维平面图和设计变量的折线图。

从图8中的Max n曲线可以看出， 其展弦比和后掠角明显小于其他外形， 这有助于降低机翼质量。 雖然降低展弦比会减小升力线斜率， 但同时大幅减小后掠角可以弥补一部分降低展弦比带来的升力损失。 对于Max R外形来讲， 巡航升阻比是其主要追求的目标， 因而其展弦比要比其他外形更大。 但考虑到增大展弦比带来的质量负担， 其展弦比仅比基准外形略大。

从BL曲线与CP曲线的相对关系可以看出， 折中点外形的展弦比略小于基准点， 同时后掠角明显减小。 这会在增大无人机升力的同时减轻其质量， 因此折中点CP外形的两项优化指标均高于基准点CP。 同时， 从图9可知基准点CP的各项性能指标均在Max n和Max R两点之间， 这进一步证明了优化前沿的有效性。

5总结

本文采用Kriging代理模型和MOEA/D算法完成了对鸭式布局截击型无人机的多目标气动外形优化设计。 优化后的外形相较于基准外形， 性能显著提高， 其中航程增大24.6%， 最大过载增大6.4%。 研究表明， 对截击型无人机， 增大展弦比有利于增大其航程， 但最大过载会有所损失； 后掠角不宜大于7°， 扭转角不宜小于-3°， 否则会导致机翼质量的显著增加， 从而影响全机性能； 鸭翼纵向位置可在6～10 cm范围内进行调整， 用于全机配平。

参考文献：

［1］ 吴静，  蔡海锋，  刘俊良. 纳卡地区冲突无人机攻防运用分析及地空反无人对策建议［J］. 现代防御技术，  2021，  49（3）： 13-20.

Wu Jing，  Cai Haifeng，  Liu Junliang. Analysis on the Operation of Attack and Defense of UAVs in Naka Conflict and Suggestions for Ground－to－Air Anti－UAVs［J］. Modern Defense Technology，  2021，  49（3）： 13-20.（in Chinese）

［2］ 张广申. 自行高炮光电系统作用距离与脱靶量仿真计算［D］. 北京： 北京工业大学， 2018.

Zhang Guangshen. Simulation Calculation of Action Distance and Miss Distance of Photoelectric System of Self－Propelled Anti Aircraft Gun［D］. Beijing： Beijing University of Technology， 2018. （in Chinese）

［3］ Lefebvre T ，  Dubot T， Joulia A. Conceptual Design Study of an Anti－Drone Drone through the Coupling of Design Process and Interception Strategy Simulations［C］∥16th AIAA Aviation Technology，  Integration，  and Operations Conference， 2016.

［4］ Hao Q，  Li W Z，  Qiu Z K，  et al. Research on Anti UAV Swarm System in Prevention of the Important Place［J］. Journal of Phy－sics： Conference Series，  2020，  1507（5）： 052020.

［5］ Coyote UAS［EB/OL］.（2022-03-22）［2022-06-05］.https：∥www.raytheonmissilesanddefense.com/what－we－do/counter－uas/effectors/coyote.

［6］ 高显忠，  王克亮，  彭新，  等. 无人机粉碎机： 硬杀伤式反无人机蜂群关键技术解析［J］. 国防科技，  2020，  41（2）： 33-38.

Gao Xianzhong，  Wang Keliang，  Peng Xin，  et al. Drone－Smasher： The Key Technology Analysis on the Manner of Hard Kill to Counter UAV Swarm［J］. National Defense Science & Technology，  2020，  41（2）： 33-38.（in Chinese）

［7］ 袁冲，  周洲. 自主拦截无人机作战效能建模与影响因素分析［J］. 火力与指挥控制，  2010，  35（6）： 114-117.

Yuan Chong，  Zhou Zhou. Operational Effectiveness Modeling and Influence Factor Analyzsis of Unmanned Independently Intercepting Air Vehicle［J］. Fire Control & Command Control，  2010，  35（6）： 114-117.（in Chinese）

［8］ 韩忠华，  张瑜，  许晨舟，  等. 基于代理模型的大型民机机翼气动优化设计［J］. 航空学报，  2019，  40（1）： 150-165.

Han Zhonghua，  Zhang Yu，  Xu Chenzhou，  et al. Aerodynamic Optimization Design of Large Civil Aircraft Wings Using Surrogate－Based Model［J］. Acta Aeronautica et Astronautica Sinica，  2019，  40（1）： 150-165.（in Chinese）

［9］ 曹粟，  蒋锋，  李易. 基于MOEA/D的三锥体拦截器气动外形优化设计［J］. 上海航天，  2019，  36（1）： 59-65.

Cao Su，  Jiang Feng，  Li Yi. Aerodynamic Optimization of Triple－Cone Interceptor Based on Decomposition－Based Multi－Objective Evolutionary Algorithm［J］. Aerospace Shanghai，  2019，  36（1）： 59-65.（in Chinese）

［10］ Zhang Q F，  Li H. MOEA/D： A Multiobjective Evolutionary Algorithm Based on Decomposition［J］. IEEE Transactions on Evolutionary Computation，  2007，  11（6）： 712-731.

［11］ Zhang Ying，  Yang Rennong，  Zuo Jialiang， et al.Improved MOEA/D for Dynamic Weapon－Target Assignment Problem［J］.哈爾滨工业大学学报： 英文版， 2015， 22（6）：121-128.

［12］ 张青斌，  丰志伟，  刘泽明，  等. 基于MOEA/D的柔性结构燃料—时间多目标优化控制研究［J］. 国防科技大学学报，  2009，  31（6）： 73-76.

Zhang Qingbin，  Feng Zhiwei，  Liu Zeming，  et al. Fuel－Time Multiobjective Optimal Control of Flexible Structures Based on MOEA/D［J］. Journal of National University of Defense Technology，  2009，  31（6）： 73-76.（in Chinese）

［13］ 方宝瑞. 飞机气动布局设计［M］. 北京： 航空工业出版社，  1997.

Fang Baorui. Aerodynamic Layout Design of Aircraft［M］. Beijing： Aviation Industry Press，  1997.（in Chinese）

［14］ 李为吉. 飞机总体设计［M］. 西安： 西北工业大学出版社，  2005.

Li Weiji. Overall Design of Aircraft［M］. Xian： Northwestern Polytechnical University Press，  2005.（in Chinese）

［15］ 杨德敏. 基于代理模型的截击型无人机气动优化设计［D］. 西安： 西北工业大学，  2022.

Yang Demin. Aerodynamic Shape Optimization of an Interception UAV Based on Surrogate Model［D］. Xian： Northwestern Polytechnical University，  2022.（in Chinese）

［16］ 李玉龙，  杨韡，  杨志刚. 鸭式布局地效飞行器纵向静稳定性数值研究［J］. 飞行力学，  2010，  28（1）： 9-12.

Li Yulong，  Yang Wei，  Yang Zhigang. Numerical Study on Longitudinal Static Stability of a Canard WIG Craft［J］. Flight Dyna－mics，  2010，  28（1）： 9-12.（in Chinese）

［17］ 袁先旭，  陈坚强，  杜雁霞，  等. 国家数值风洞（NNW）工程中的CFD基础科学问题研究进展［J］. 航空学报，  2021，  42（9）： 23-40.

Yuan Xianxu，  Chen Jianqiang，  Du Yanxia，  et al. Research Progress on Fundamental CFD Issues in National Numerical Windtunnel Project［J］. Acta Aeronautica et Astronautica Sinica，  2021，  42（9）： 23-40.（in Chinese）

［18］ 高歌，  闫文辉，  吴俊宏，  等. 计算流体力学——典型算法与算例［M］. 北京： 机械工业出版社，  2015.

Gao Ge，  Yan Wenhui，  Wu Junhong，  el al. Comuptational Fluid Dynamics－Typical Algorithms and Examples［M］. Beijing： China Machine Press，  2015.（in Chinese）

［19］ Mei Y，  Tang K，  Yao X. Decomposition－Based Memetic Algorithm for Multiobjective Capacitated Arc Routing Problem［J］. IEEE Transactions on Evolutionary Computation，  2011，  15（2）： 151-165.

［20］ Lophaven S N，  Nielsen H B，  Sondergaard J. DACE： A MATLAB Kriging Toolbox［R］.Technical University of Denmark，  2002.

［21］ 韓忠华. Kriging模型及代理优化算法研究进展［J］. 航空学报，  2016，  37（11）： 3197-3225.

Han Zhonghua. Kriging Surrogate Model and Its Application to Design Optimization： A Review of Recent Progress［J］. Acta Aeronautica et Astronautica Sinica，  2016，  37（11）： 3197-3225.（in Chinese）

［22］ 赵璇，  常思江，  张哲玮，  等. 滑翔制导炮弹气动-弹道综合优化方法［J］. 航空兵器，  2022，  29（4）： 48-57.

Zhao Xuan，  Chang Sijiang，  Zhang Zhewei，  et al. Comprehensive Optimization Method of Aerodynamic and Trajectory for Gliding Guided Projectile［J］. Aero Weaponry，  2022，  29（4）： 48-57.（in Chinese）

［23］ 赵璇，  常思江，  倪旖. 滑翔制导炮弹鸭舵的气动外形快速优化研究［J］. 航空兵器，  2021，  28（5）： 99-105.

Zhao Xuan，  Chang Sijiang，  Ni Yi. Research on the Rapid Aerodynamic Shape Optimization of Canards of Gliding Guided Projectile［J］. Aero Weaponry，  2021，  28（5）： 99-105.（in Chinese）

［24］ 胡劲，  刘涛，  张鹏，  等. 巡飞武器气动/结构/隐身一体化设计及多学科优化设计［J］. 航空兵器，  2016（3）： 9-13.

Hu Jin，  Liu Tao，  Zhang Peng，  et al. Aerodynamics/Structure/Invisibility Integrative Design and Multidisciplinary Design Optimization of Loitering Weapon［J］. Aero Weaponry，  2016（3）： 9-13.（in Chinese）

Optimization Design of Multi－Objective Aerodynamic Shape of a Intercepting UAV

Yang Demin1，  Lin Sanchun2，  Li Yi1， 3

（1. Shanxi Aerospace Flight Vehicle Design Key Laboratory，  Northwestern Polytechnical University， Xian 710072，  China;

2. Beijing Institute of Space System Engineering，  Beijing 100076，  China;

3. Yangtze River Delta Research Institute， Northwestern Polytechnical University， Taicang 215411，  China）

Abstract： Using drones to intercepting drones is an effective and affordable means of countering UAVs. In this paper，  for a canard interceptor UAV，  the Reynolds－averaged N－S equation （RANS） is used to calculate the flow field，  and the Kriging surrogate model and the decomposition－based multi－objective evolutionary algorithm （MOEA/D） are used to carry out the aerodynamic shape optimization design. In the optimization work，  the range and the maximum available overload are taken as the design goals，  the longitudinal position of the canard，  the twist angle of the main wing，  the aspect ratio and the sweep angle are taken as the design variables，  and the static stability and the maximum deflection angle of the canard are constrained，  and the cost is relatively high. Less computing resources get a uniformly distributed Pareto front，  and the optimized range and maximum available overload of the unmanned aerial vehicle have increased by 24.6% and 6.4% respectively compared to the benchmark shape，  proving the effectiveness of this optimization method.

Key words： counter－UAVs; canard layout; Kriging surrogate model; decomposition based multi－objective genetic algorithm （MOEA/D） ; multi－objective  optimization

收稿日期： 2022-06-05

基金項目： 航天科技联合基金项目

作者简介： 杨德敏（1998-）， 男， 山东郓城人， 硕士研究生。

*通信作者： 李易（1984-）， 男， 河南郑州人， 副教授。