基于SPH方法的瞬态非等温黏弹性Couette流的数值模拟

2023-07-19许晓阳赵雨婷

应用数学和力学 2023年6期

许晓阳, 赵雨婷

(西安科技大学计算机科学与技术学院,西安 710054)

0 引言

黏弹性流动广泛存在于自然界和工业加工中,如挤压成型、注塑成型等[1]．这些流动一般呈现非等温状态,因此有必要考虑温度模型[2]．深入研究黏弹性流体的非等温流动机理具有重要的学术价值和应用意义,但由于其多物理场耦合的复杂性和黏弹流变特性的复杂性,实验和解析求解均难以完成,因此数值模拟成为一种可替代的研究途径．

目前,基于网格的数值方法已被应用于此类问题的数值模拟中．Meburger等[3]用非结构网格有限体积法(finite volume method,FVM)模拟了非等温黏弹性流体在高Weissenberg数下的流动．Moreno等[4]用变分多尺度稳定有限元法分析了温度对黏弹性流动的影响．Gao[5]用相场模型对非等温聚合物填充过程进行了有限元计算．

SPH[6-7]方法是一种Lagrange型的无网格数值方法．与基于网格的数值方法相比,SPH方法不仅免去了生成网格的繁琐,而且避免了传统Lagrange方法中网格扭曲、重构等问题[8]．近年来,随着SPH方法计算精度的提高和稳定性的改善,该方法已被较多地应用于溃坝[9]、爆炸[10]、液体晃荡[11]和流固耦合[12]等问题的数值模拟中．然而,对于黏弹性流动问题的数值模拟,由于其非线性黏弹本构方程的引入,极大地增加了问题求解的复杂度,因此相关文献研究报道较少．2005年,Ellero等[13]首次进行了等温条件下黏弹性流动的SPH模拟,其中采用Oldroyd-B模型来描述流体的黏弹性行为．Fang等[14]将SPH方法推广到了含自由面的瞬态等温黏弹性液滴下落问题的数值模拟中．Murashima等[15]提出了多尺度SPH方法研究支化聚合物熔体绕圆柱形障碍物的流动．杨波等[16]运用SPH方法数值模拟了基于Oldroyd-B模型的平面突然起动Couette流．Xu等[17]提出了一种改进SPH方法,对等温黏弹性液滴和挤出胀大问题进行了研究．King等[18]将对数构象公式与应力分裂技术相结合,提出了模拟黏弹性流动的不可压SPH方法．Duque-Daza等[19]将SPH与流体流动模拟的等效弹性势能结合在一起,建立了黏弹性流体建模与计算的简化方法．Vahabi等[20]用弱可压SPH方法模拟了Oldroyd-B黏弹性溶液中两个初始圆形的气泡在上升过程中的相互作用．根据文献调研结果,目前应用SPH方法对黏弹性流动问题开展的模拟研究大多是在等温情况下进行的,而工业生产中的黏弹性流动通常是非等温流动,因此有必要开展非等温黏弹性流动的数值模拟．

本文在文献[17]的基础上,运用SPH方法对瞬态非等温黏弹性流动问题进行了数值模拟研究．首先,模拟了等温情况下基于Oldroyd-B模型的黏弹性Couette流动;随后,将其扩展到非等温情况下进行模拟,其中选用Reynolds指数模型来评估黏度和松弛时间的温度依赖．通过与有限体积方法解的比较和对数值收敛性的评价,验证了SPH方法模拟非等温黏弹性流动问题的准确性和有效性．讨论了非等温流动相较于等温流动的不同流动特征,分析了温度依赖系数、Péclet数等对黏弹性流动过程的影响．

1 控制方程

在Lagrange坐标系下,非等温黏弹性流体的控制方程组可表示为[21]

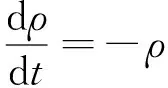
(1)

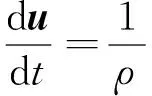
(2)

(3)

式中,d/dt为物质导数,ρ为流体密度,t为时间,u为速度,σ为总应力张量,F为外力,cp为定压比热容,T为温度,κ为导热系数．值得注意的是,本文仅考虑纯受迫流动,浮升力相对于惯性力很小,因此忽略了自然对流[22]．

总应力张量σ可分解为各向同性压力、溶剂贡献和聚合物贡献之和:

σ=-pI+2ηsd+τ,

(4)

其中,I为单位矩阵,ηs为溶剂黏度,τ表示弹性偏应力张量,d为形变率张量,

(5)

通过对总应力张量的分解,方程(2)可表示为

(6)

1.1 Oldroyd-B本构方程

对于弹性偏应力张量τ,考虑如下微分形式的Oldroyd-B本构方程:

(7)

式中,λ表示流体的松弛时间;ηp表示聚合物黏度．ηs和ηp满足如下关系:

η=ηs+ηp,

(8)

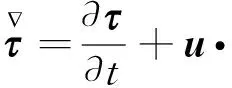
(9)

综合式(7)和(9),有

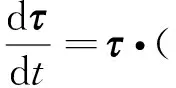
(10)

对于流体松弛时间和黏度的温度依赖,选用Reynolds指数模型进行建模和计算:

ηs(T)=ηse-φ(T-T0),

(11)

ηp(T)=ηpe-φ(T-T0),

(12)

λ(T)=λe-φ(T-T0),

(13)

其中,φ为温度依赖系数,T0为参考温度．另外,为了更好地描述流动,引入以下无量纲数:Péclet数Pe=ρcpVL/κ、Reynolds数Re=ρVL/η、Weissenberg数Wi=λV/L、溶剂黏度比β=ηs/η,其中V和L分别表示流动的特征速度和特征长度．

1.2 状态方程

SPH方法常采用状态方程来模拟弱可压缩流动．本文使用的状态方程如下[23]:

(14)

其中,ρ0为参考密度,c为声速,γ=7．为了保证弱可压缩流动行为足够接近不可压缩流动行为,声速c通常选择比最大流体速度大10倍左右．

2 SPH方法

2.1 SPH离散

对于质量和动量守恒方程,本文采用的SPH离散为[24]

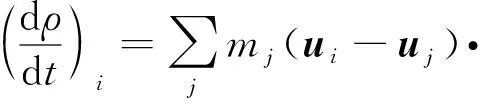
(15)

(16)

式中,i表示粒子编号,j为粒子i的相邻粒子,Wij=W(|rij|,h)为核函数,rij=ri-rj,ri为粒子i的位置,h为光滑长度．由于五次样条核函数具有连续的二阶导数,其精度和稳定性均较好,故本文选用它作为核函数,其表达式如下:

(17)

其中,q=r/h,对于二维问题W0取值7/(478πh2)．

对于Oldroyd-B本构方程,其SPH离散取决于速度偏导数的离散．引入

(18)

于是,Oldroyd-B本构方程的SPH离散可表示为

(19)

传统SPH方法的计算精度低,限制了其向更复杂流动问题的应用．为了提高计算精度,本文对SPH离散(15)—(19)中的核函数梯度进行修正,即利用修正矩阵[25]

(20)

将原核函数梯度修正为

(21)

利用新的核梯度(21)进行计算,可提高SPH方法的计算精度．关于核梯度修正SPH离散的更多内容,可参阅文献[24]．

2.1.1 温度方程的离散

若要实现非等温黏弹性流动问题的SPH模拟,还需对温度方程进行SPH离散．对于温度方程(3),其等号右端部分涉及Laplace算子的离散化．通常,可采用SPH散度算子和梯度算子的离散对Laplace算子进行离散,但其所产生核函数的二阶导数对粒子的无序性十分敏感,容易引起数值计算的不稳定．借鉴Shao和Lo[26]对Laplace算子离散的思想,本文对温度方程采用如下的SPH离散格式:

(22)

2.2 边界处理

2.2.1 固壁边界

由于边界或邻近边界处的粒子在积分时会被边界截断,这种单向影响会导致求解错误,因此有必要对固壁边界进行特殊处理．

本文采用由固壁粒子和固壁外虚粒子组成的增强型处理技术[9]．首先,沿固壁边界以粒子初始间距Δx布置一层固壁粒子．在计算过程中,固壁粒子参与控制方程中速度、压力和弹性应力的计算,以有效地防止粒子穿透边界．固壁粒子的密度和位置均保持不变,压力和弹性应力通过其支持域内流体粒子压力和弹性应力的正则化插值得到:

(23)

其中,B表示压力或弹性应力,i表示固壁粒子,j表示与固壁粒子i相邻的流体粒子．

其次,为弥补边界处粒子在积分时被边界截断的问题,在固壁边界外以粒子初始间距Δx额外布置3层固壁外虚粒子．与边界粒子类似,固壁外虚粒子的密度和位置也保持不变．为满足压力和弹性应力的Neumann边界条件,固壁外虚粒子的压力和弹性应力设置为与边界法向上相链接的固壁粒子值相同,如图1所示．

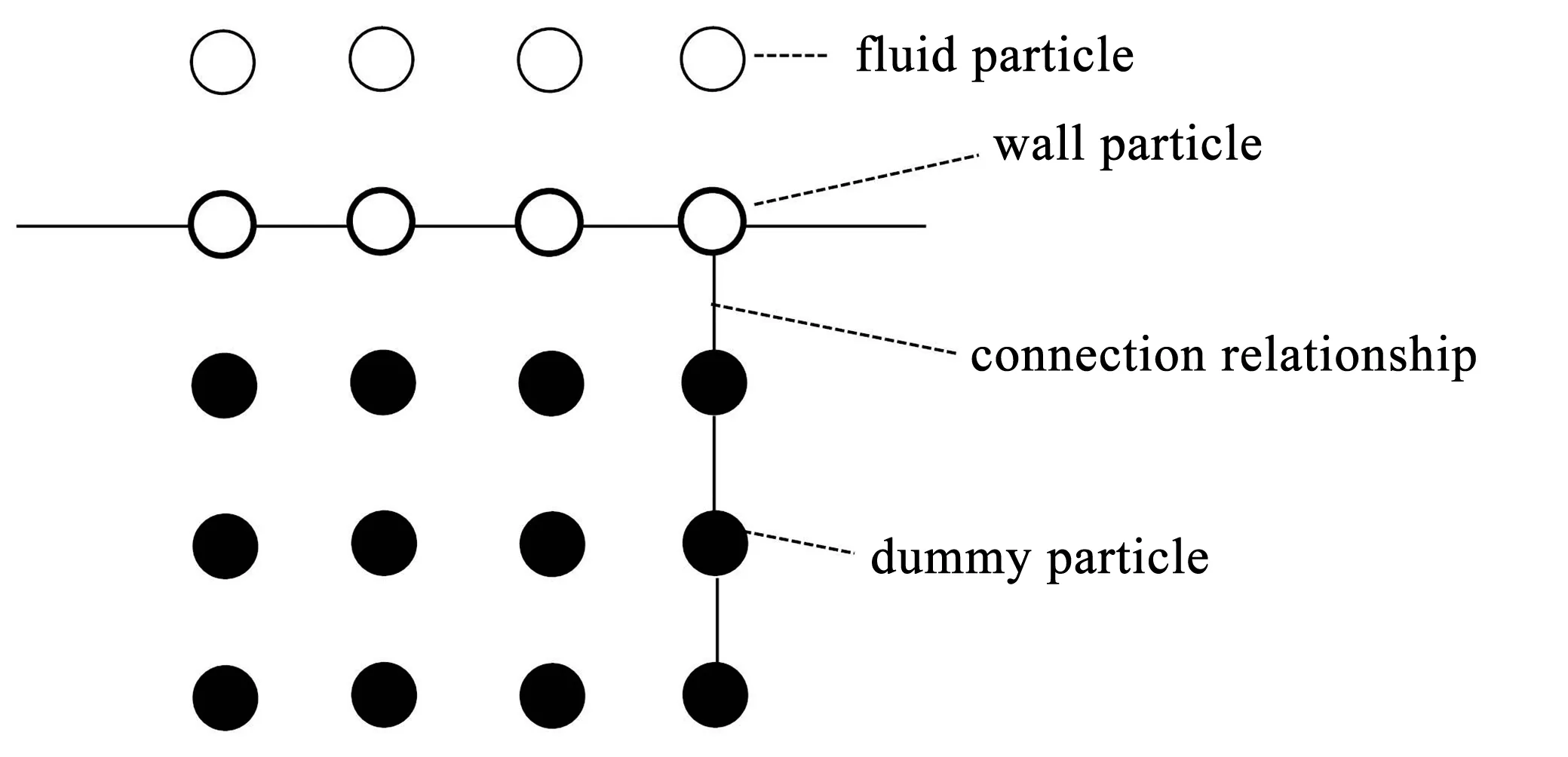
图1 固壁边界处理示意图Fig.1 Sketch of the wall boundary treatment

2.2.2 周期边界

对于黏弹性Couette流动的模拟,采用周期边界条件进行无限长平板的处理．在粒子运动过程中,沿x方向施加周期边界条件,其实施步骤如下:在每一时间步,通过右侧边界离开流域的SPH粒子将从左侧边界在相同的y位置重新插入流域;左侧边界周围的流体粒子被定义为右侧边界附近粒子的相邻粒子,反之亦然．

2.3 时间积分

由于蛙跳积分法具有存储需求量低、计算效率高的优点,因此本文选用该方法进行时间积分．关于该积分格式的详细内容,可参阅文献[8]．

3 黏弹性Couette流模拟

鉴于目前尚未见到运用SPH方法对基于Oldroyd-B模型的非等温黏弹性Couette流动问题进行数值模拟的文献报道,因此本文选用该问题作为数值算例,并讨论非等温流动相较于等温流动的不同流动特征,分析各物理参数对流动过程的影响．

3.1 等温流动

首先考虑等温流动．图2给出了该问题的几何模型和初始状态．当t=0时,流体是静止的,且位于两块固定、垂直间距为L的无限长平板之间;当t>0时,上平板突然以平行于x轴正方向的恒定速度u0运动．

图2 黏弹性Couette流的几何区域Fig.2 The geometric region of the viscoelastic Couette flow

模拟中,沿x轴方向采用周期边界约束,故计算区域可取为Lx×Ly=0.5×1．上平板速度u0=1,流体密度ρ=1,各物理参数取值为Re= 0.1,Wi=0.1,β= 0.1,其中特征长度L=1,特征速度V=1．粒子初始间距设置为Δx=0.02,对应于1 274个流体粒子,64个固壁粒子和192个固壁外虚粒子．核函数采用五次样条函数,光滑长度采用与Ellero等[13]模拟黏弹性Poiseuille流相同的取值,即h=0.9Δx．声速c=10V,时间步长Δt=1.0×10-5．选用3个空间点A,B和C记录流体的瞬态流动行为,它们到下平板的高度分别为0.25L,0.5L和0.75L．对于该问题,本文用联想计算机(Intel(R) Core(TM) i7-9700 CPU@3.60 GHz)模拟10万个时间步,所耗时间约为983 s．

图3给出了黏弹性Couette流动在t=1时刻的粒子分布和速度分布;而图4给出了A,B和C三点处的速度u和弹性剪切应力τxy随时间的变化情况,并将本文SPH数值解和解析解[27]进行了比较．可以看出,由于受弹性作用的影响,Couette流发生了明显的速度过冲．A,B和C三点处的速度u均经历了先增大、后减小,逐渐达到稳态的过程;离上平板越近,稳态时的速度值越大．点C处的稳态速度值明显高于点A和B处的稳态速度值．对于剪切应力,离上平板越近,应力发生的时间越早,但稳态时的剪切应力值几乎相同．无论对于速度u还是剪切应力τxy,SPH数值解与解析解均吻合,从而验证了本文SPH方法求解黏弹性流体的有效性和准确性．

图3 等温黏弹性Couette流动在t=1时刻的粒子分布和速度分布Fig.3 The particle distribution and the velocity distribution of the isothermal viscoelastic Couette flow at t=1

(a) 速度u (b) 弹性剪切应力τxy(a) Velocity u (b) Elastic shear stress τxy图4 等温黏弹性Couette流动A,B,C三点处的速度u和弹性剪切应力τxy随时间的变化:SPH数值解与解析解的对比Fig.4 Isothermal viscoelastic Couette flows at 3 points A,B and C:a comparison of SPH and analytical solutions for velocity u and elastic shear stress τxy

图5给出了Re=1和10时点B处的速度u和弹性剪切应力τxy随时间的变化情况,其他参数保持不变．可以看出,即便对于较大的Re,本文SPH方法也能够精确稳定地模拟．对于Re=1和10,所得SPH数值解和解析解均吻合较好．另外,Re越大,速度过冲现象越不明显,但稳态值几乎相同．这是因为:Re越大,流动惯性力越占优,导致弹性力所占比重下降,因此速度的过冲现象减弱．Re越大,剪切应力稳态值越小,这是因为:Re越大,流体黏度越小,导致应力计算的稳态值也越小．

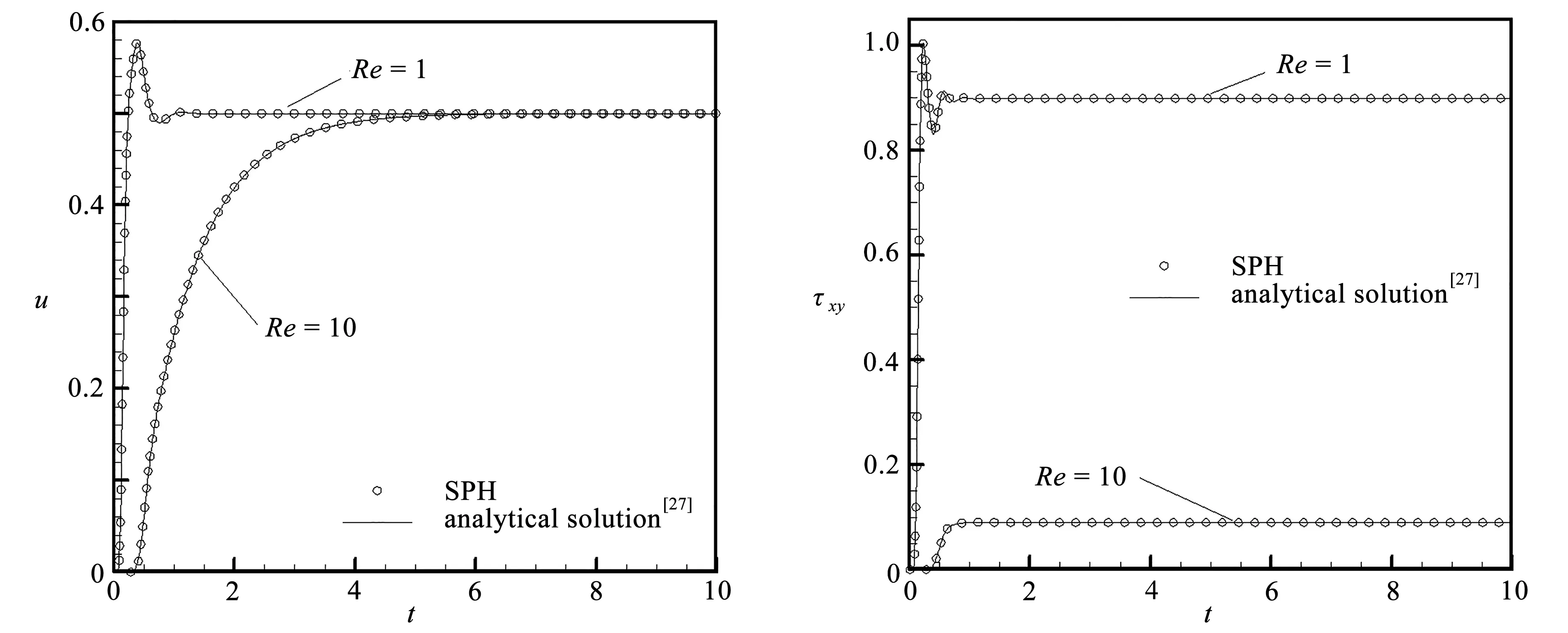
(a) 速度u (b) 弹性剪切应力τxy(a) Velocity u (b) Elastic shear stress τxy图5 Re=1和10时,等温黏弹性Couette流动的SPH模拟:点B处的速度u和弹性剪切应力τxy随时间的变化Fig.5 SPH simulations of isothermal viscoelastic Couette flows with Re=1 and 10:the time changes of velocity u and elastic shear stress τxy at point B

3.2 非等温流动

接下来,我们将黏弹性Couette流动扩展到非等温情况下进行模拟．取流体温度和下平板温度Tf=313,上平板温度Tw=443,温度依赖系数φ=0.001,Péclet数Pe=100．模拟过程中,其他参数均设置为与等温流动相同．

图6给出了非等温情况下点B处的速度u和弹性剪切应力τxy随时间的变化情况,并将非等温结果与等温结果进行了比较．在流动早期阶段,非等温和等温情况的流动特征几乎相同;但在t>1之后,温度的引入对流体的流动特征产生了一定的影响．等温流动在t=1时刻已达到了稳态,但非等温流动的速度和剪切应力值均出现轻微下降,这表明非等温流动并未达到热平衡．该下降趋势一直持续下去,即便在t=2时刻,非等温流动仍未达到稳态．为了分析温度依赖系数φ对流动过程的影响,本文特别增加了φ=0.005和0.010的数值试验,其他参数均保持不变．从图 6可以看出,φ越大,流动后期速度和剪切应力的下降趋势越明显．这表明:温度依赖系数对流动过程的影响随着φ的增加而愈加明显．但即便对于较大的φ= 0.010,流动在t=2仍未达到稳态．

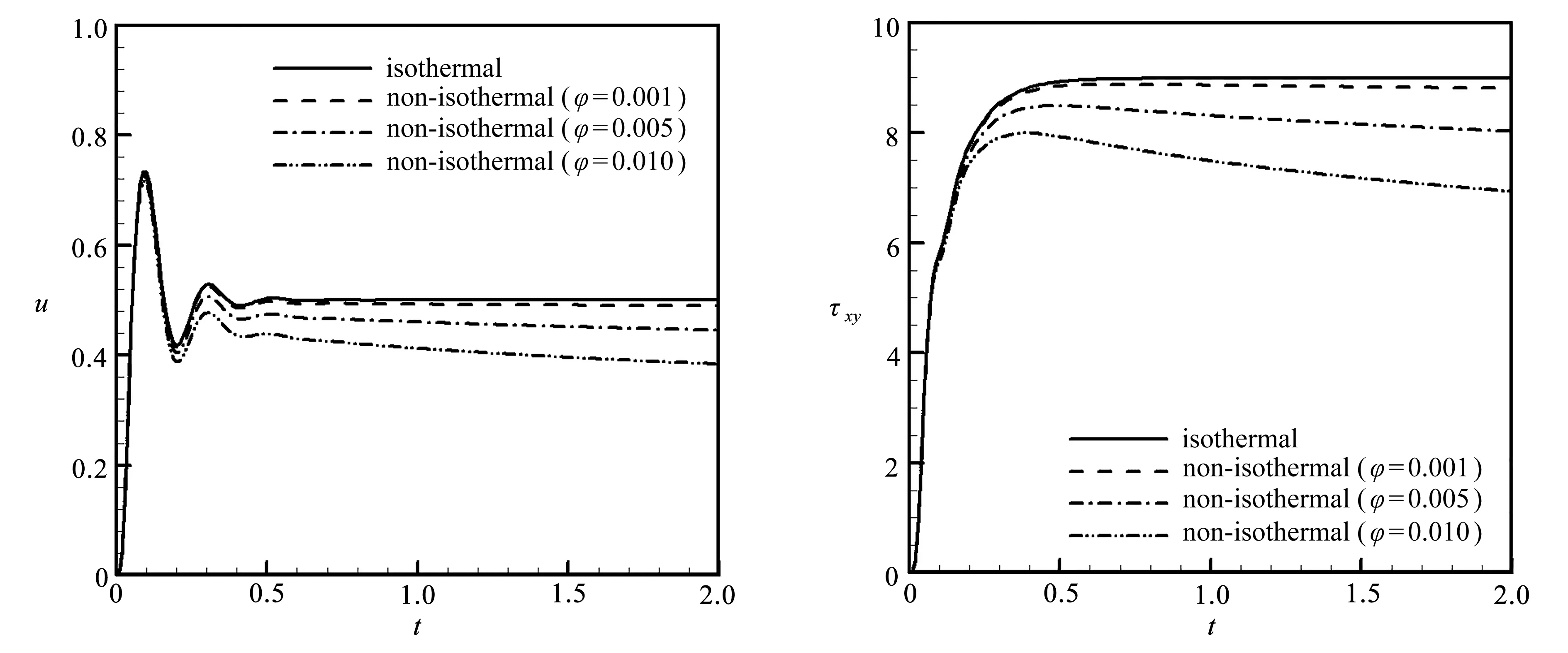
(a) 速度u (b) 弹性剪切应力τxy(a) Velocity u (b) Elastic shear stress τxy图6 非等温黏弹性Couette流的SPH模拟:φ对点B处速度u和弹性剪切应力τxy随时间变化的影响Fig.6 The SPH simulation of the non-isothermal viscoelastic Couette flow:the effect of temperature dependent parameter φ on the time changes of velocity u and elastic shear stress τxy at point B

由于φ越大,流动后期速度和弹性剪切应力的下降趋势越明显,因此接下来本文选取较大的φ= 0.01,研究Pe对流动过程的影响．图7给出了3个不同Pe(Pe=1,20,100)下点B处的速度u和弹性剪切应力τxy随时间的变化情况．可以看出,Pe越小,流动达到稳态所需的时间越短．对于Pe=1,速度u和弹性剪切应力τxy在t=1时刻已达到稳态,但Pe=20和100还没有．这是因为,Péclet数表示对流速率与扩散速率之比,Pe越小,比热容越小,流体热扩散越快,流动会更快地达到热平衡．为了检验Pe=1时的流动在t=1时刻是否已达到热平衡,图8给出了Couette流动在6个不同时刻的温度关于y的分布情况．流动初期,热量由上平板向下传递,流体温度随之升高;在t=1时刻,流体温度呈线性分布,这表明Couette流动在此时刻已经达到热平衡．值得注意的是,对于Pe=20和100的算例,流动在达到热平衡后也可以达到稳态,只是所需的时间更长．

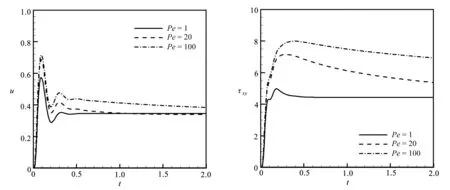
(a) 速度u (b) 弹性剪切应力τxy(a) Velocity u (b) Elastic shear stress τxy图7 非等温黏弹性Couette流的SPH模拟:Pe对点B处速度u和弹性剪切应力τxy随时间变化的影响Fig.7 The SPH simulation of the non-isothermal viscoelastic Couette flow:the effect of Pe on the time changes of velocity u and elastic shear stress τxy at point B

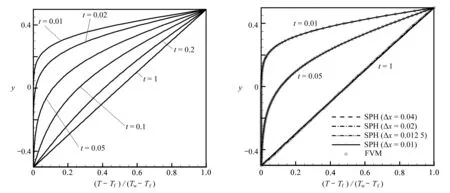
图8 非等温黏弹性Couette流的SPH模拟(Pe=1,φ=0.01):6个不同时刻的温度关于y的分布图9 利用SPH得到的温度分布图的收敛性分析及其与FVM解的比较Fig.8 The SPH simulation of the non-isothermal viscoelastic Couette flow (Pe=1,φ=0.01):the temperature distribution vs.y at 6 different moments Fig.9 Convergence analysis of the temperature distribution obtained with the SPH and the comparison with the FVM solution

为了验证本文SPH方法求解非等温黏弹性流动问题的有效性,图9给出了Pe=1和φ=0.01时,利用SPH方法和FVM方法[28]得到的3个不同时刻温度分布图的比较．不难看出,SPH解和FVM解吻合较好．另外,为了验证本文SPH方法求解非等温黏弹性流动问题的数值收敛性,本文特别增加了粒子初始间距分别为Δx=0.01,0.012 5,0.04的数值试验,其他参数均保持不变,得到的温度分布图如图 9所示．可以看出,通过3组不同粒子初始间距和原始粒子初始间距(Δx=0.02)得到的温度分布结果无显著差异．上述结果表明,本文SPH方法对于非等温黏弹性流动问题的模拟是准确、收敛的．

3.2.1β的影响

β表示溶剂黏度与流体总黏度之比．为了进一步研究β对流动过程的影响,图10给出了不同β(β=0.05,0.10,0.30,0.50)取值下点B处的速度u和弹性剪切应力τxy随时间的变化情况．图10中的各物理参数取值如下:Re=0.1,Wi=0.1,Pe=1,φ=0.01,因为此时流动可较快地达到热平衡．可以看出,β并不影响速度的稳态值,但显著影响速度的瞬态行为．β越大,速度的过冲现象越不明显．这一结果表明:β较小,即溶剂黏度比总黏度小得多时,此时弹性占优,因此对黏弹性瞬态流动的影响较大;反之,当β增大时,弹性作用对流动的影响减小．对于弹性剪切应力τxy,其稳态值随着β的增大而减小,这是因为:β越大,流体越接近于Newton流体,弹性力越弱．

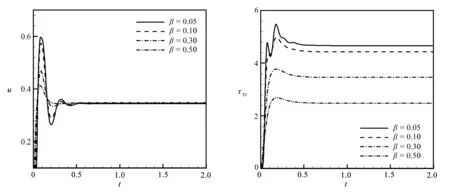
(a) 速度u (b) 弹性剪切应力τxy(a) Velocity u (b) Elastic shear stress τxy图10 非等温黏弹性Couette流的SPH模拟:β对点B处速度u和弹性剪切应力τxy随时间变化的影响Fig.10 The SPH simulation of the non-isothermal viscoelastic Couette flow:the effect of β on the time changes of velocity u and elastic shear stress τxy at point B

3.2.2Wi的影响

Wi是黏弹性流动的另一个重要参数．它比较了弹性力与黏性力,通常由流体的应力松弛时间与具体的加工时间的关系给出．为了研究Wi对流动产生的影响,图 11给出了Re=0.1,β= 0.1,Pe=1和φ=0.01时,不同Wi取值下(Wi=0.05,0.10,0.20,0.50)点B处的速度u和弹性剪切应力τxy随时间的变化情况．可以看出,Wi对速度瞬态行为的影响较大,但并不影响稳态值的大小．Wi越大,速度过冲现象越明显,达到最值所需时间也越长．对于Wi=0.05,0.10,0.20,0.50,速度过冲达到的最值分别为umax≈0.520,0.575,0.615,0.640,而达到最值所需的时间分别为t≈0.06,0.10,0.12,0.20．对于较大的Wi=0.5,还观察到2次明显的速度过冲．

(a) 速度u (b) 弹性剪切应力τxy(a) Velocity u (b) Elastic shear stress τxy图11 非等温黏弹性Couette流的SPH模拟:Wi对点B处速度u和弹性剪切应力τxy随时间变化的影响Fig.11 The SPH simulation of the non-isothermal viscoelastic Couette flow:the effect of Wi on the time changes of velocity u and elastic shear stress τxy at point B

对于弹性剪切应力,我们观察到随着Wi的增大,流动前期的剪切应力值逐渐变小．特别是对于Wi=0.05的试验,其剪切应力很快达到稳态;但当Wi=0.5时,其剪切应力比Wi=0.05的小,且在持续增长．Wi越大,剪切应力达到稳态值所需的时间越长,但它并不改变其稳态值的大小．对于Wi=0.05,0.10,0.20,0.50,剪切应力达到稳态值所需的时间分别为0.69,0.78,0.91,1.51．这是因为,Wi越大,流体的应力松弛时间越长．在这种情况下,流动需要更长的时间来达到稳态．