基于有理插值方法模拟SMAs循环加载下的变形行为
2023-07-19王晓明
王晓明, 肖 衡
(1.宁波职业技术学院 应用力学研究所,浙江 宁波 315000;2.暨南大学 力学和建筑工程学院,广州 510632)
0 引 言
因具有独特的形状记忆效应(shape memory effect,SME)、伪弹性(pseudo-elasticity,PE)、拉伸-压缩不对称以及生物兼容性等特征,形状记忆合金(SMAs)被广泛应用于航天航空[1]、机器人制造[2]、生物医疗[3]等领域.SMAs构件在实际使用过程中往往需要受到反复加载-卸载的作用,应力-应变关系从一开始的塑性变形逐渐转变为伪弹性变形.通过构建SMAs本构模型,模拟其在循环荷载作用下的变形行为,具有十分重大的工程价值.
SMAs自从被发现以来就受到了巨大的关注,尤其是近几十年来,其本构建模的理论不断被提出,综述文献也有很多[4-9],我们大致可以将这些理论分为三大类,即微观模型、介观模型和宏观模型.微观模型在晶格和晶粒尺度上描述晶核生长、马氏体孪晶生长等特征.其中,Falk[10-11]基于Ginzburg-Landau理论提出了多项式[12]势能模型.Daw等[13]运用分子动力学理论构建了SMAs微结构模型.介观模型首先需要建立微观尺度下的本构关系,然后通过平均方法等尺度转换方法建立宏观本构.其中,Wang等[14]基于马氏体相变[15-16]和晶体塑性理论构建了三维模型,研究了马氏体塑性变形产生的不可恢复变形.Taylor等[17]引入微平面理论,认为SMAs的多轴宏观力学行为是不同取向微平面单轴相应的叠加.该方法随后被用于模拟超弹性、伪弹性行为[18].宏观模型不再考虑材料内部结构理论,而是从宏观特征出发推导本构方程.其中,Tanaka[19]利用非线性弹性方法构建了一个一维本构模型,其马氏体体积分数演化方程通过一种分段方程给出;Brinson[20]进一步发展了他的理论,将马氏体体积分数分解为自适应部分和非自适应部分;Lagoudas等[21]利用弹塑性理论构建了SMAs宏观本构,马氏体相变、退孪晶等热力学过程受到加载函数和流动法则的影响; Zaki等[22]通过热力学势函数构建了三维模型,引入了三个新的内变量来解释循环作用下的SMAs“训练”(training)和双程形状记忆效应(TWSME).
近几十年以来,关于SMAs循环荷载作用下的实验研究有很多[22-24].这些实验结果表明,循环荷载下,马氏体在正相变、逆相变作用下,塑性不可恢复变形逐渐累计,相变转化初始应力和耗散能逐渐减少,相变硬化逐渐增大.每一个循环下的应力-应变关系从初始的塑性变形,逐渐转化为伪弹性变形.当循环达到一定量以后,应力-应变滞回圈趋于一种稳定状态,且累计的塑性变形等量变成饱和状态.通过透射电子显微镜(TEM)技术研究循环作用下SMAs的微观结构,科研工作者们发现,不可恢复变形累积的主要微观机制是奥氏体相的滑移和不完全拟相变形成的残余马氏体相[25].
在实验的基础上,众多学者提出了SMAs本构模型对循环加载下的变形行为进行模拟,可参考综述文献[26].这些模型分别从宏观唯象和微结构机制两个方向进行建模.早期的唯象模型[4,20,27]只考虑了循环作用下的马氏体相变,无法模拟塑性应变累积、残余马氏体相退化等情况.Bo和Lagoudas[28-30]在原模型的基础上,引入了新的内变量来表征马氏体相变和塑性变形相互作用产生的影响,提出了一个改进的模型;Auricchio等[31-32]考虑了相变阀值和残余变形量,模拟了SMAs的“训练”和双程形状记忆效应;Zaki和Moumni[33]引入了马氏体体积分数和马氏体定向应变张量两个状态变量来解释伪弹性和单程形状记忆效应,后续又提出了包括累积马氏体体积分数在内的三个新的内变量来表征循环加载下的变形特征.另外,微结构理论从SMAs微观机制推导模拟循环加载变形.Patoor等[34-35]基于物理应变机制和局部热力学势的定义构建了动力学表述的微结构模型,马氏体体积分数作为内变量用来描述内结构状态的演化;Huang等[36]发展了一种单晶模型,利用一定数量随机方向的单晶颗粒通过平均方法构建了多晶SMAs本构模型;Lagoudas和Entchev[37]提出了一个致密SMAs三维本构模型,用来解释循环荷载下的相变、塑性应变以及滞回圈形状和大小的演化规律;Kang等[38]通过“应变控制”的循环加载实验发现了SMAs的荆轮变形行为.随后,Yu等[39-40]基于晶体塑性理论解释了循环加载下的非弹性变形机制,如马氏体相变、相变诱导塑性、马氏体再定向等.
以上模型在模拟循环加载下SMAs塑性变形和伪弹性变形的时候,通常需要分别引入额外的内变量,这些量的演化方程需要引入多个隐式参数,这就给计算带来了非常大的挑战.为了解决以上问题,一种显式方法被提出,用于构造SMAs和类橡胶材类的本构模型[40-49].本文在之前研究[50]的基础上,基于有理插值的方法,提出了一种新的有限弹塑性J2流模型,用来同时精确模拟SMAs在循环荷载下的塑性变形和伪弹性变形.
全文主要安排如下:首先,基于有理插值的方法给出了循环加载下的形函数形式,对任意形状的应力-应变滞回圈都能精确模拟;其次,构建了新的有限弹塑性J2流模型;再次,从单轴情况出发,经过多轴扩展、局部因子引入等步骤,得到了多轴有效的硬化模量显式表达;最后,选取经典的实验数据和新模型得到的结果进行对比,证明了该方法的有效性,并给出了结论.
1 基于有理插值的形函数
在控制最大应力不变的前提下,对SMAs试件进行反复加载-卸载,其应力-应变关系如图1所示.先分析循环荷载下应力-应变关系的特征,再分别分析每一次循环过程中,加载和卸载情况下的形函数,最后利用有理插值具体给出屈服阶段的形函数表达,对任意形状的应力-应变滞回圈都可以精确模拟.使用的应力为Kirchhoff应力,应变为对数应变,也称为Hencky应变,并用有效塑性功代替传统的塑性功.
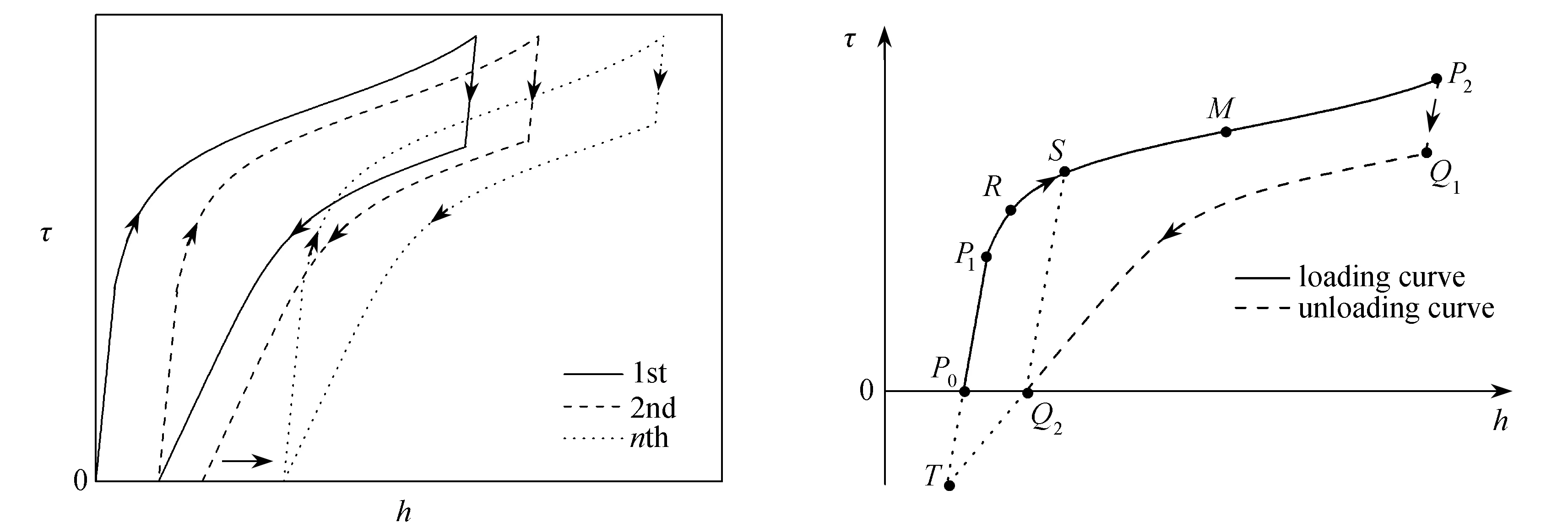
图1 循环荷载下的应力-应变示意图 图2 第i次循环下的应力-应变示意图Fig.1 Schematic of stress-strain curves under cyclic loading Fig.2 Schematic of stress-strain curve in the ith cycle
1.1 循环荷载下的变形特征
图1表示从第1次到第n次循环下的应力-应变关系.对图1分析可知,循环荷载下SMAs应力-应变关系特征如下:
1) 每一次加载-卸载循环都会形成一个不完全封闭的滞回圈.从第一个循环到最后一个循环总共产生n个应力-应变滞回圈,其中第n个循环已经完全封闭且稳定.
2) 每一个应力-应变滞回圈由加载和卸载两部分组成.其中,加载部分包括弹性阶段和上屈服阶段,卸载部分包括弹性阶段和下屈服阶段.
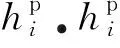
4) 当循环次数接近甚至到达n时,应力-应变滞回圈稳定,且不可恢复变形量不再继续增加,此时
1.2 加载和卸载阶段形函数
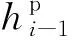
(1)
点P1表示加载部分从弹性阶段变成屈服阶段的过渡点,该点的应力即为屈服强度,用r0表示,应变用h0i表示,而有效塑性功与点P0一样,为ϑi-1.P1P2段表示加载部分的屈服阶段,也就是上屈服阶段,该段的应力-应变形函数用
(2)

(3)
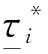
(4)
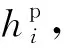
形函数中关键点应力、应变和有效塑性功如表1所示.根据式(1)—(4)可得
(5)

表1 形函数中关键点应力、应变和有效塑性功Table 1 Stresses,strains and effective plastic works of key points in the shape function
1.3 上下屈服形函数关系
笔者之前的研究中[47]用了一种线性关系来表示上下屈服应力之间的一一对应关系,即为
(6)
任意一个下屈服形函数中的点必然有一个点和上屈服形函数对应,比如图2中的点T对应点P1,点Q2对应点S,点Q1对应点P2.其中bi是可调参数,若bi=1,则表示上下屈服形函数平行,这种情况可以处理简单的伪弹性特性[41],而μ0i则表示图2中点S所对应的应力大小.
利用方程(2)、(4)和(6),得到上下屈服形函数之间的关系为
(7)
即只要给定上屈服形函数的具体形式,就可以通过方程(7)推导得到下屈服形函数.
1.4 基于双曲正切函数的有理插值方法
基于双曲正切函数的形函数形式,可以精确匹配上屈服流的应力-应变数据,其具体形式为
(8)
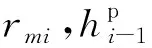
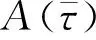
(9)
将方程(8)代入到方程(7)中,可以得到下屈服段的形函数,其中涉及到的两个关键参数为bi和μ0i.接下来给出这两个参数的确定方法.
(10)
从以上方程可以得到
(11)
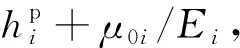
(12)
利用方程(9)可得
(13)
2 有限弹塑性J2流模型
有限弹塑性本构模型的类型有很多,本文采用基于对数客观率的表述形式[51].首先通过伸缩率分解的形式给出基本方程,然后耦合强化效应,改进背应力演化方程.
2.1 基于伸缩率分解的基本方程
基于Euler表述的有限弹塑性模型满足自洽条件[51],其基本方程是基于伸缩率的分解的形式,即
D=De+Dp,
(14)
其中D为速度梯度的对称部分,也就是伸缩率,De表示弹性部分,Dp表示塑性部分.
弹性部分可以通过Hooke定律给出
(15)
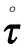
(16)
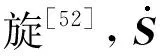
塑性部分通过流动法则[53]给出:
(17)
式中,ξ表示塑性指数,加载情况下,其值为1,卸载情况下为0,u表示塑性模量,f表示von Mises屈服函数,其表达式为
(18)
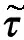
2.2 强化效应耦合
有效塑性功随着塑性流的发展单调递增,且和热力学内耗散直接相关.因此本文用有效塑性功代替传统的塑性功,其表达为
(19)
为了使本构模型耦合屈服面半径大小和屈服中心移动,屈服强度r不仅依赖于有效塑性功ϑ,还和背应力相关,即
r=r(ϑ,ζ),
(20)
其中ζ的大小完全依赖背应力张量,其表达为
(21)
背应力的演化方程遵循新的各向异性强化法则:
(22)
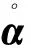
(23)
方程(20)和(23)确保了模型耦合两种强化效应,3个硬化含函数c,ω和r的具体形式将在第3节中给出.接下来需要确定塑性模量u的表示,可以由以下公式推导[47]:
(24)
其中4阶张量H为
(25)
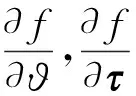
(26)
其中
3 硬 化 函 数
为了从第2节构建的有限弹塑性J2流模型中推导得到符合要求的结果,需要给出硬化函数c,ω和r的具体形式.首先推导得到单个循环下的硬化函数形式,再给出有效塑性功的演化规律,最后引入依赖塑性功的局部因子,构造统一光滑的硬化函数显式表达.
3.1 单个循环下的硬化函数
单循环下的硬化函数推导需要从塑性坡度出发,利用方程特点分别给出ci,ωi和ri,再通过推导相邻循环下屈服函数的表达,证明其符合内循环一致性条件.
3.1.1 塑性坡度
由方程(17)、(18)、(19),再结合塑性模量的表达(方程(24)),推导得到单轴情况下有
(27)
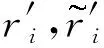
(28)
方程(27)和(28)给定的形式只是单轴有效,为了扩展成多轴有效,需要将塑性坡度改进为
[ri+Λi]=0.5(ri+Λi+|ri+Λi|).
(29)
将改进后的塑性坡度代入到方程(27),得到单个循环下多轴有效的形式为
(30)
3.1.2ci,ωi和ri
将方程(30)转化为以下形式:
(31)
以上方程要得到有效的ωi,必须满足分子和分母同时为0,即
(32)
从方程(32)可以推导得到
(33)
将方程(33)代入到方程(31),得到
(34)
接下来考虑屈服极限ri的表达.在Xiao[41,48]和Wang等[42]研究的基础上,进一步考虑有效塑性功的局部性特点,得到屈服极限表达为
(35)
式中,r0表示初始屈服强度,两个非负参数β2和β3分别表示ζ=0和ϑ=ϑi(或ϑi+1)的局部特征,
μi=(r0-μ0i)/bi,i=1,2,3,…,n.
(36)
3.2 有效塑性功演化规律
从第1次循环开始,到第n次循环结束,每一次循环都伴随着有效塑性功的累计,本小节给出其在循环荷载下的演化规律.用ϑi(i=1,2,3,…,n)表示每一次循环结束后的有效塑性功大小.
根据方程(35)和(36),在忽略局部特征的前提下,得到单循环下塑性强度为
(37)
(38)
根据方程(14)、(15)和(17),在单轴情况下的塑性应变为
(39)
根据方程(6),单轴下的有效塑性功为
(40)
将方程(39)代入到方程(40),再结合屈服条件,得到
(41)
对方程(41)进行积分,并结合方程(8)形函数的形式,可以得到单个循环下,图2中累计的有效塑性功大小,在μ0i∈[r0,r+rmi)的情况下为
ϑi=ϑi-1+2Z1-Z2,ϑ0=0,i=2,3,…,n,
(42)
其中
(43)
在μ0i∈[r+rmi,∞)的情况下为
ϑi=ϑi-1+2Z1-(Z0+Z3),ϑ0=0,i=2,3,…,n,
(44)
其中
(45)
上屈服阶段P1P2之间必然有一个点的应力为r0+rmi,假设该点用M表示,如图2所示.Z1表示P1-P2阶段累计的有效塑性功,也等于Q1-T阶段积累的有效塑性功;在μ0i∈[r0,r+rmi)的情况下,点S在点M前面,Z2表示P1-S阶段累计的有效塑性功,也等于Q2-T阶段积累的有效塑性功; 在μ0i∈[r+rmi,∞)情况下,点S在点M后面,Z3表示M-S阶段累计的有效塑性功,Z0表示P1-M阶段积累的有效塑性功.因此,Z0+Z3可以表示P1-S阶段的有效塑性功,也等于Q2到T的有效塑性功,其效果和μ0i∈[r0,r+rmi)情况下的Z2一样.
3.3 统一光滑硬化函数
式(31)、(33)和(35)分别给出了每一个循环下的ci,ωi和ri,i=1,2,3,…,n.本小节在前面的基础上构造一个光滑统一的硬化函数表达,使其对n个循环过程均适用.
这里通过n个局部因子,将得到的所有单循环硬化函数进行简单的线性插值,得到
(46)
其中,局部因子具体形式为
(47)
φi具备如下特点:当有效塑性功ϑ∈[ϑi,ϑi+1)时,其值为1,其他情况下均为0.由此可得,在第i次循环下硬化函数自动退化为ci,ωi和ri.
4 模型结果与实验结果对比
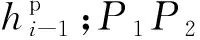
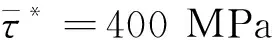
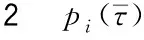
表2 中固定参数值Table 2 Values of fixed parameters in
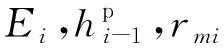
(48)
其中ϑ=0,表示第1次循环的情况,此时i=1.在本例中μ0i∈[r0,r+rmi),每一个循环下的有效塑性功结合方程(42)和(43)给出,代入到方程(48)就可以得到每一循环下的参数值.再利用方程(13)就能确定μ0i的大小,最终得到的模型结果和实验结果如图3所示.
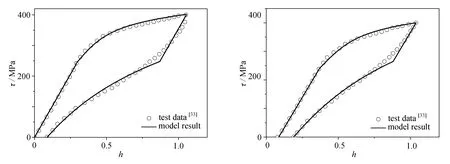
(a) 第1个循环 (b) 第2个循环(a) The 1st cycle (b) The 2nd cycle
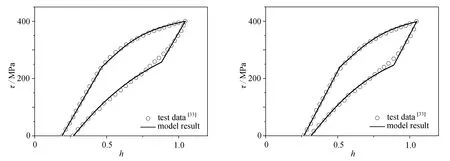
(c) 第3个循环 (d) 第4个循环(c) The 3rd cycle (d) The 4th cycle
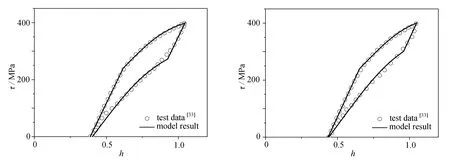
(e) 第8个循环 (f) 第12个循环(e) The 8th cycle (f) The 12th cycle
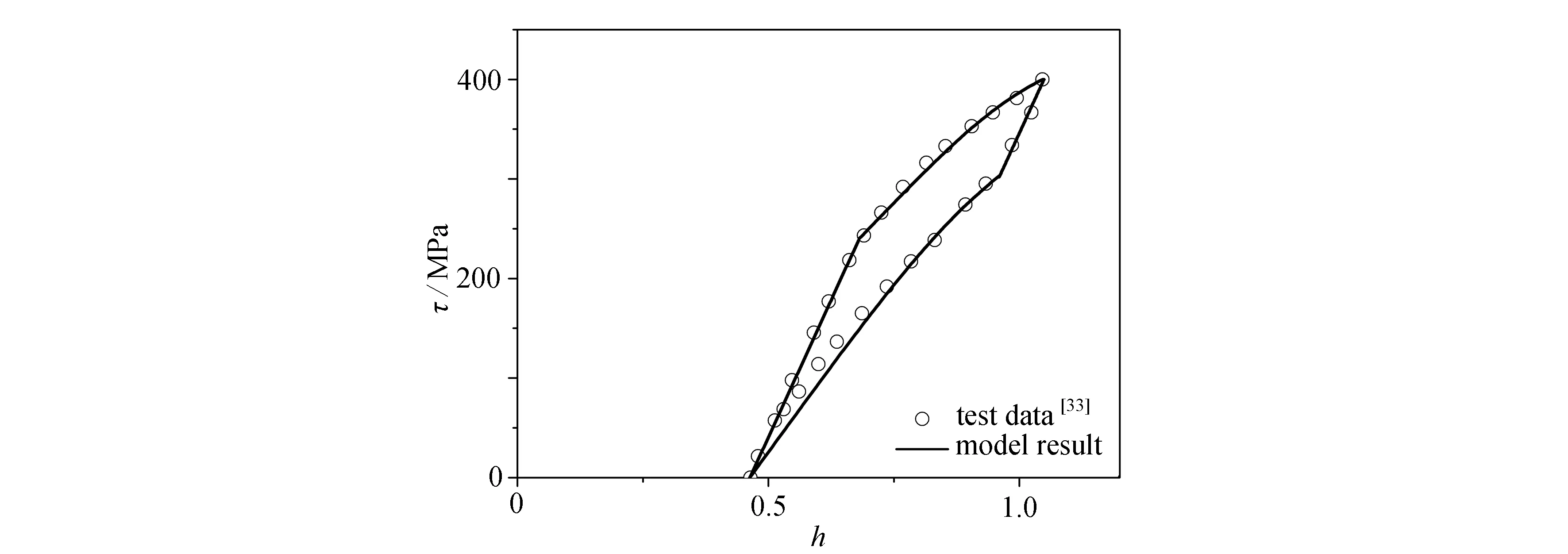
(g) 第20个循环(g) The 20th cycle图3 第1、2、3、4、8、12和20次循环的模型结果和实验结果[33]对比Fig.3 Comparation between model results and experimental data[33] for the 1st,2nd,3rd,4th,8th,12th and 20th cycles
模型预测结果如图4所示.其中由外到内的实线分别表示第4、5、6、7和8次的模型结果.其中第4和第8次的结果和实验数据可以精确匹配(从图3(d)、3(e)数据对比可得),而第5、6和7次的实验数据,新的模型可以合理地预测.第5次循环开始时的应变和第4次结束时一致,而第7次循环结束时的应变和第8次开始时一致.
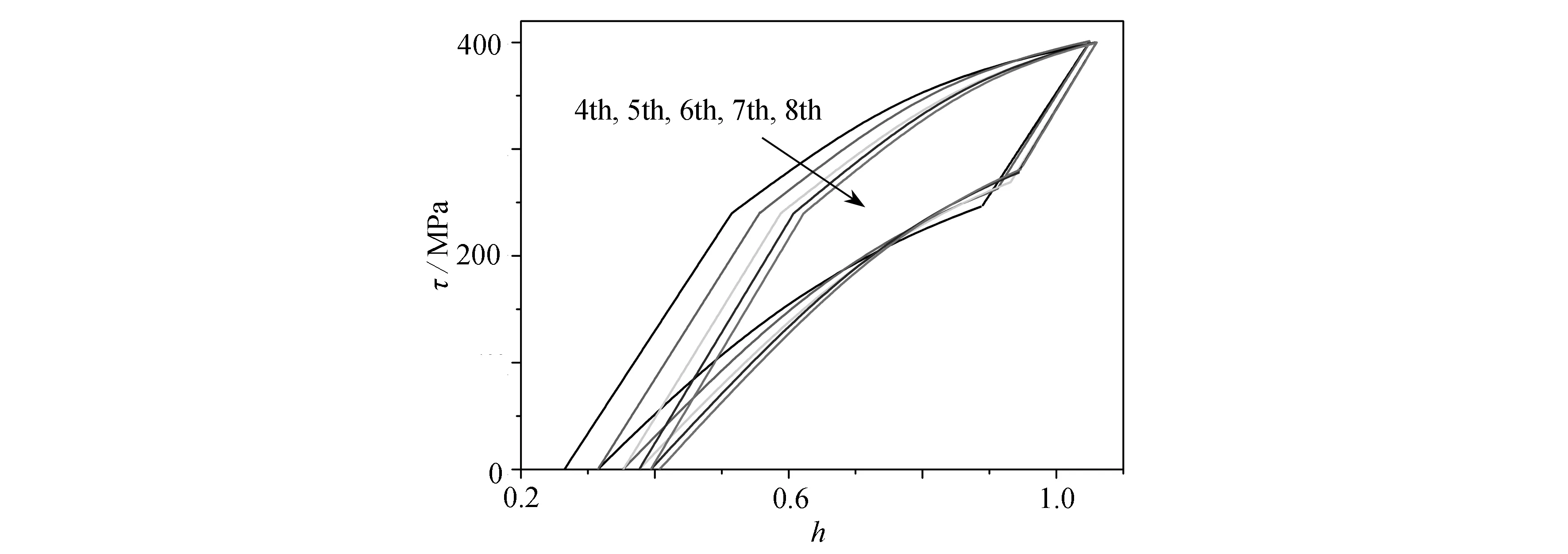
图4 第4至第8个循环的模型预测Fig.4 Model predictions from the 4th to the 8th cycles
5 结 论
本文通过提出新的有限弹塑性J2流方程,模拟了SMAs在循环荷载下从塑性变形逐渐转化为伪弹性变形的过程.所得主要结论如下:
1) 新的本构方程耦合了屈服中心的移动和屈服面的增大,使得模型可以模拟SMAs复杂的变形行为.传统的金属材料在加载后卸载,卸载阶段的应力-应变关系一般遵循Hooke定律.卸载应力到0以后进行反向加载才会开始出现下屈服阶段,也就是Bauschinger效应.本文通过改进背应力的演化方程,提出硬化模量c,ω和r的新形式,使得SMAs在卸载应力为0之前就开始屈服,进而产生滞回圈.
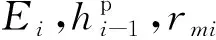
3) 从第2节的基本方程出发,结合形函数具体形式,得到了有效塑性功的演化规律,如方程(43)和(45)所示.利用这些方程可以得到每一个循环下ϑ的累积大小,进而通过方程(49)给出的参数方程,确定该循环下的参数值,从而得到循环的应力-应变滞回圈.
4) 由局部因子构造而成的统一光滑硬化模量c,ω和r如方程(47)所示,这些量在单循环下会自动退化成符合要求的形式,将这些硬化模量代入到本构方程以后,能够得到符合要求的结果.通过图3的模型结果和实验结果比较,证明了本文方法得到的结果可以精确匹配实验结果.此外,对于没有采集实验数据的循环,利用方程(49)推导的参数也可以进行合理地预测,如图4所示.
致谢本文作者衷心感谢宁波职业技术学院研究机构专项课题(NZ21JG008)对本文的资助.
