AO-LSSVM在铣削铝合金表面粗糙度预测研究与应用
2023-07-17吕亮亮尹凝霞仵景岳麦青群刘璨
吕亮亮 尹凝霞 仵景岳 麦青群 刘璨
(广东海洋大学机械工程学院,湛江 524088)
文摘 为提高铣削7475 铝合金表面粗糙度(Ra)的预测准确性和便捷性,本文基于天鹰优化器算法(AO)对最小二乘向量机(LSSVM)进行优化,以4个铣削参数作为输入值,Ra作为输出值构建铣削铝合金Ra预测模型,通过与粒子群(PSO)优化最小二乘支持向量机(LSSVM)和LSSVM 两种算法进行对比,采用灰色关联对铣削参数与表面粗糙度之间的相关性进行分析并通过GUI 界面搭建Ra 预测系统。结果表明:基于AOLSSVM的Ra 预测模型的预测误差为4.287 6%,拟合优度达到0.938 64,优于其他算法;每齿进给量与Ra 的相关性最大,灰色关联度值为0.764;通过GUI预测应用系统能实现高效、便捷、准确地预测Ra值。
0 引言
7475铝合金由于其质量轻、耐腐蚀、较强的抗疲劳断裂等特性,广泛应用于飞机、汽车和医疗器械[1]等领域,与其他铝合金相比(如7050 和7075 铝合金)具有更好的机械性能[2]。这些应用领域对零件表面加工质量要求较高,表面粗糙度(Ra)对机械产品的使用寿命和可靠性有重大影响,它会直接影响摩擦条件从而影响工件的腐蚀、磨损、疲劳和类似的其他属性[3-4],所以高效、可靠、精确的Ra预测对于现代制造业的表面质量控制至关重要。
目前Ra预测研究可分为3 大领域[5]。(1)基于加工理论的理论模型:张宇鑫等[6]基于未变形切削厚度模型并引入氧化膜厚度的影响构建Ra预测模型,其准确度达到91.25%;S.YANG等[7]建立了考虑碳纤维分布的外周铣削碳纤维增强聚合物的Ra预测模型,其理论公式包含运动学、动力学和碳纤维分布,Ra的预测精度达到90.05%;G.WANG等[8]考虑毛坯的初始粗糙度、接触法向压力和尺寸效应的因素的影响,建立了考虑尺寸效应的微成型Ra预测模型,陈超逸等[9]提出一种分段的Ra理论预测模型。(2)基于实验设计的回归模型:李韩博等[10]基于响应曲面法构建二阶回归模型预测SPIF(单点增量成型)Ra;时强胜等[11]基于GRA-RSM 构建橡胶垫磨抛Ra预测方法。(3)基于人工智能的模型:S.LI等[12]基于粒子群算法优化最小二乘支持向量机,以噪声、振动和工件表面纹理的特征值作为输入值,粗糙度作为输出值构建多维特征融合的Ra预测模型,该模型的预测精度达到92.54%;史丽晨等[13]基于残差网络自适应提取能力强的优点,提出一种基于小波变换结合残差网络构建Ra的预测方法;R.WANG等[14]提出一种新的遗传算法集成学习模型,应用于316不锈钢多喷射抛光中的Ra预测,平均误差从0.215 下降到0.195。K.MANJUNATH等[15]基于长短期记忆预测S45C 钢铣削过程中的Ra,其均方根误差函数为0.109 7。上述3 大领域中基于理论模型的预测建模建立在观测到的物理现象,与实际现象有一定的偏差;基于实验设计的回归模型依赖于设计方法,有一定的局限性;而基于人工智能的预测模型侧重于数据的挖掘,没有设计方法的局限性。
为了进一步提高铣削铝合金Ra的预测准确性,本文基于天鹰优化算法(aquila optimizer,AO)优化最小二乘支持向量机(least squares support vector machine,LSSVM)构建Ra预测模型,采用灰色关联分析法分析Ra与4 个铣削参数之间的相关性。为了快速便捷地预测,在MATLAB 开发环境中构建Ra预测应用系统,该系统以AO-LSSVM 预测模型为核心,并镶嵌响应曲面算法作为分析铣削参数与Ra之间的响应曲面关系。
1 基于AO-LSSVM 表面粗糙度预测模型的建立
1.1 LSSVM 回归模型
LSSVM 是一种新的机器学习方法[12],是对标准支持向量机(support vector machines,SVM)的改进[16]。它具有学习速度快,泛化能力强的优点,可以避免神经网络的过度拟合和SVM 训练时间长的问题[17],故本文使用LSSVM 作为铣削铝合金Ra的预测模型,其主要原理如下[18]:对于记录输入参数xi和输出参数yi的样本组U={(xi,yi)|i=1,2,3,…,n},使用从输入空间到输出空间的非线性映射构造LSSVM的回归函数,公式如下[12]:
式中,ω表示权重向量;φ(x)表示非线性映射函数;b为预设偏置常数。
根据结构最小化原理,LSSVM 目标函数和约束条件设置如下[12]
式中,γ表示正则化参数;ei表示回归函数的输出与结果之间的误差。为了解决LSSVM 的受限优化问题,引入拉格朗日常数将式(2)转换成更容易求解的对偶空间优化模型式(3):
式中,αi为拉格朗日乘数。将式(3)的偏导数取为ω,b,e和α得到最优条件等式[17]:
通过消除式(4)中的ω和ei,可以获取所需的优化解[17]:
式中,E=(1,1,…,1)T;Ω为核函数矩阵;I是单位矩阵;y=(y1,…,yi)T。核函数表达式为[17]:
特征空间的训练数据分布取决于映射非线性输入空间的核函数选择[19],径向基函数(RBF)由于其强大的逼近能力和学习速度广泛用于回归模型,故本研究中使用非线性系统中RBF函数作为LSSVM的核函数,RBF核定义如下[12]:
式中,σ为核函数的宽度系数。因此,用于函数近似的LSSVM模型的最终公式如下[17]:
LSSVM 模型的拟合能力主要取决于最优惩罚因子γ与核参数平方σ2的选择质量,其中γ和σ2影响LSSVM的泛化性能,γ的选择直接影响整个模型的计算复杂度和稳定性。为了避免模型的过度拟合并确保可靠性能,应适当设置最优惩罚因子γ与核函数宽度值σ,在本研究中,使用AO 算法优化来获得LSSVM模型的适当参数。
1.2 AO-LSSVM 预测模型建立
1.2.1 AO优化算法
AO 优化算法具有多个探索和开发策略以及强大的多元化能力,能够以较短的时间收敛和较强的鲁棒性[20]。AO算法优化原理如下。
(1)扩展探索,天鹰鸟群通过高空翱翔识别猎物区域、扩大搜寻范围并通过垂直俯冲选择最佳狩猎区域,该部分的数学公式为[20]:
式中,X1(t+1)为t+1 次迭代的解;Xbest(t)为第t次迭代为止算法获得的最优解,反映了猎物的最佳位置;t和T分别为当前迭代次数和最大迭代次数;XM(t)表示第t次迭代时种群平均位置;A为0~1 之间的随机值;Dim为问题维度的大小。
(2)缩小探索,当AO 鸟群在高空发现猎物时,鸟群会在目标猎物上方盘旋,准备着陆,然后进行攻击,其目的为缩小狩猎范围,即缩小最优解的搜索空间,其数学公式表达为[20]:
式中,L(D)为莱维飞行分布函数,D为维度空间;XR(t)为第i次迭代时取[1,N]范围内的随机解;s为固定为0.01的常数值;u和ν是0~1之间的随机数。(3)扩大开发,AO 利用目标的选定区域来接近猎物,通过垂直下降的方法进行初步攻击试探猎物的反应,该部分行为的数学公式为[20]:
式中,α和δ为开发调整参数,由于本文Ra数据值偏小,故将参数固定为较小值0.1;LB表示给定问题的下限,UB表示给定问题的上限。
(4)缩小开发,当AO接近猎物时,AO根据其随机运动在陆地上攻击猎物,行走和抓取猎物的数学公式为[20]:
式中,QF表示用于平衡搜索策略的质量函数;G1表示在追踪猎物过程中天鹰的各种运动;G2表示线性递减的飞行斜率值,范围是[0,2];X(t)是第t次迭代的当前解。
1.2.2 AO-LSSVM 建模
最优惩罚因子γ与核参数平方σ2为LSSVM 最重要的参数,直接影响铣削铝合金表面粗糙度建模的准确性与稳定性。将LSSVM 的训练集均方根误差(RMSE)作为AO 优化器算法的适应度值,将惩罚因子与核参数平方作为超参数,利用AO 优化器算法进行寻优。AO算法优化LSSVM流程如图1所示。
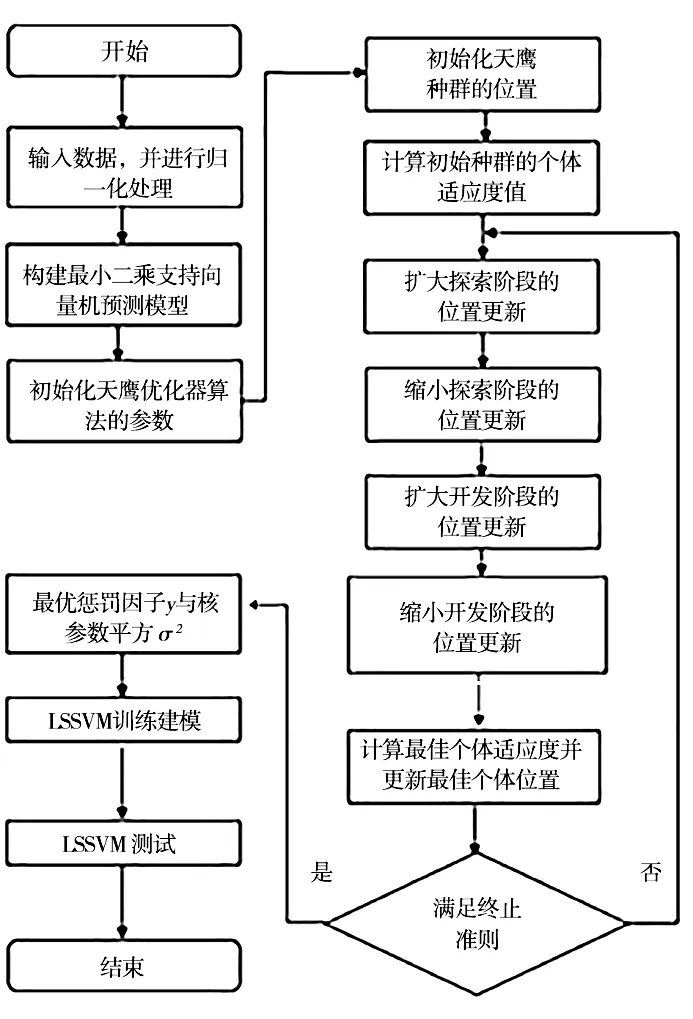
图1 AO-LSSVM算法流程图Fig.1 Flow chart of AO-LSSVM algorithm
2 表面粗糙度预测模型实例分析
2.1 表面粗糙度预测影响因素分析
Tipins 等人在1976 年建立的Ra预测经验模型仅包含主轴转速n、每齿进给量f、轴向切深ap数[21]。文献[22]基于PSO-LSSVM 构建的预测模型也仅包含上述3个切削参数,为了使预测模型预测更为准确和考虑的切削影响因素更为全面,国内外学者对铣削加工的Ra进行了试验研究[23-25],研究发现构建铣削Ra预测模型时应当考虑径向切深ae的影响。
基于以上分析,本文选择n、f、ap及径向切深ae作为输入值构建Ra预测模型。
2.2 表面粗糙度实验数据获取
本研究中构建铣削铝合金Ra预测模型的45 组实验数据均来自课题组实验数据[26],实验设计方案采用正交实验和响应曲面两种实验设计方法,实验参数水平表如表1所示。

表1 表面粗糙度实验因数与水平Tab.1 Experimental factors and levels of surface roughness
实验设备采用VMC1000P 立式加工中心和 Mar Surf PS1 手持式Ra测试仪。实验材料为7475 铝合金,刀具采用直径D=10 mm、z=4、前角为5°、后角15°、螺旋角30°的整体式硬质合金立铣刀,实验采用平面顺铣和乳化液冷却的切削方式,加工过程图片如图2所示。为了减小测量误差,在已加工表面的不同位置选取3段,每次测量长度为5.6 mm,测量4次,Ra取平均值,实验所得数据如表2所示。
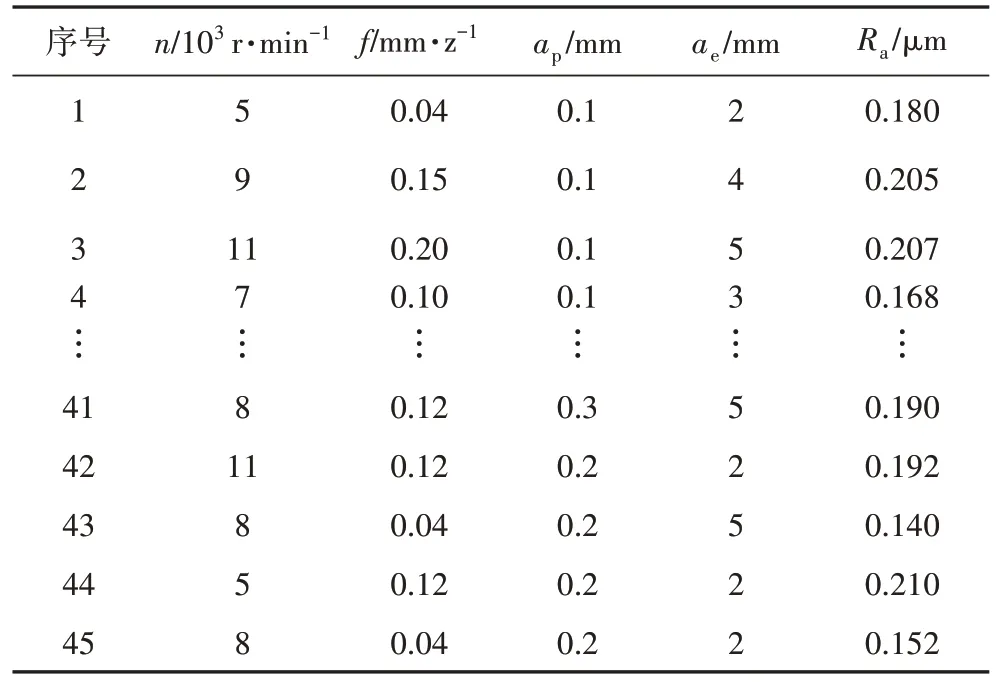
表2 表面粗糙度实验数据Tab.2 Experimental data of surface roughness

图2 铝合金铣削加工示意图Fig.2 Aluminum alloy milling schematic
2.3 粗糙度与铣削参数的灰色关联分析
灰色相对关联度是根据因子序列与初始点的变化率发展趋势判断序列之间的相似关联度[12]。本文采用灰色关联分析来描述4 个铣削参数与粗糙度之间的相关性。灰色相对关联度值越接近于1,表明影响因子与粗糙度之间的关系越显著。采用SPSSAU在线数据分析软件对45 组数据进行灰色关联度分析,选用Ra为参考数列,4 个铣削因素为比较数列。数据归一化处理后计算灰色关联系数,公式如下:
式中,ξi(k)为比较数列xi对参考数列x0在第k个指标上的关联系数;ρ为分辨系数,通常取0.5;minimink|x0(k) -xi(k)|、maximaxk|x0(k) -xi(k)|分别为两级最小差和两级最大差。记:
则式(13)转换为式(14):
由式(14)得到45组铣削实验数据的灰色关联系数,然后对45组数据计算其灰色关联度,不同铣削参数对Ra的关联度计算公式如下:
铣削铝合金的Ra灰色关联分析结果如表3 所示,部分加工后的表面形貌如图3 所示,可知每齿进给量为0.04 的工件加工后的表面形貌最好。由表3可知,每齿进给量与Ra的灰色关联度值为0.764,而其他3 个铣削参数的灰色关联度值相差不大均在0.65左右。关联度结果表明每齿进给量是影响铣削平面Ra的最大因素。

表3 关联度结果Tab.3 Correlation results

图3 主轴转速为8 000 r/min的部分加工后的表面形貌 20×Fig.3 Surface topography after partial machining with spindle speed of 8 000 r/min
3 AO-LSSVM 的表面粗糙度预测性能评估
为了验证本文基于AO-LSSVM 建立的铣削铝合金Ra预测模型的预测准确率及泛化能力,使用粒子群(particle swarm optimization,PSO)优 化LSSVM(PSO-LSSVM)、LSSVM 与AO-LSSVMRa预测模型进行对比分析。将获得的45组Ra实验数据导入到AO-LSSVM 预测模型中,与使用相同实验数据的PSO-LSSVM 和LSSVM 进行对比分析。AO-LSSVM与PSO-LSSVM 的进化曲线如图4 所示,AO-LSSVM相较于PSO-LSSVM收敛速度快、迭代次数少。
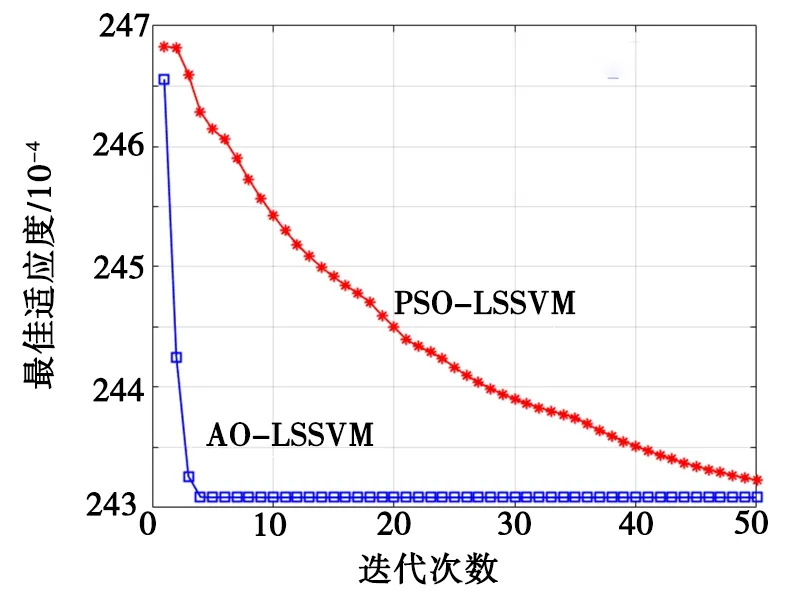
图4 AO-LSSVM与PSO-LSSVM的进化曲线Fig.4 Evolution curves of AO-LSSVM and PSO-LSSVM
选用平均绝对误差(MAE)、均方根误差(RMSE)和平均绝对百分比误差(MAPE)作为Ra预测模型的性能评价指标,其公式分别为:
不同预测模型的Ra预测结果如图5、图6 所示,测试集误差分析结果如表4所示。

表4 测试集误差分析Fig.4 Test set error analysis

图5 AO-LSSVM、PSO-LSSVM、LSSVM训练集性能评估图Fig.5 AO-LSSVM,PSO-LSSVM,LSSVM training set performance evaluation chart
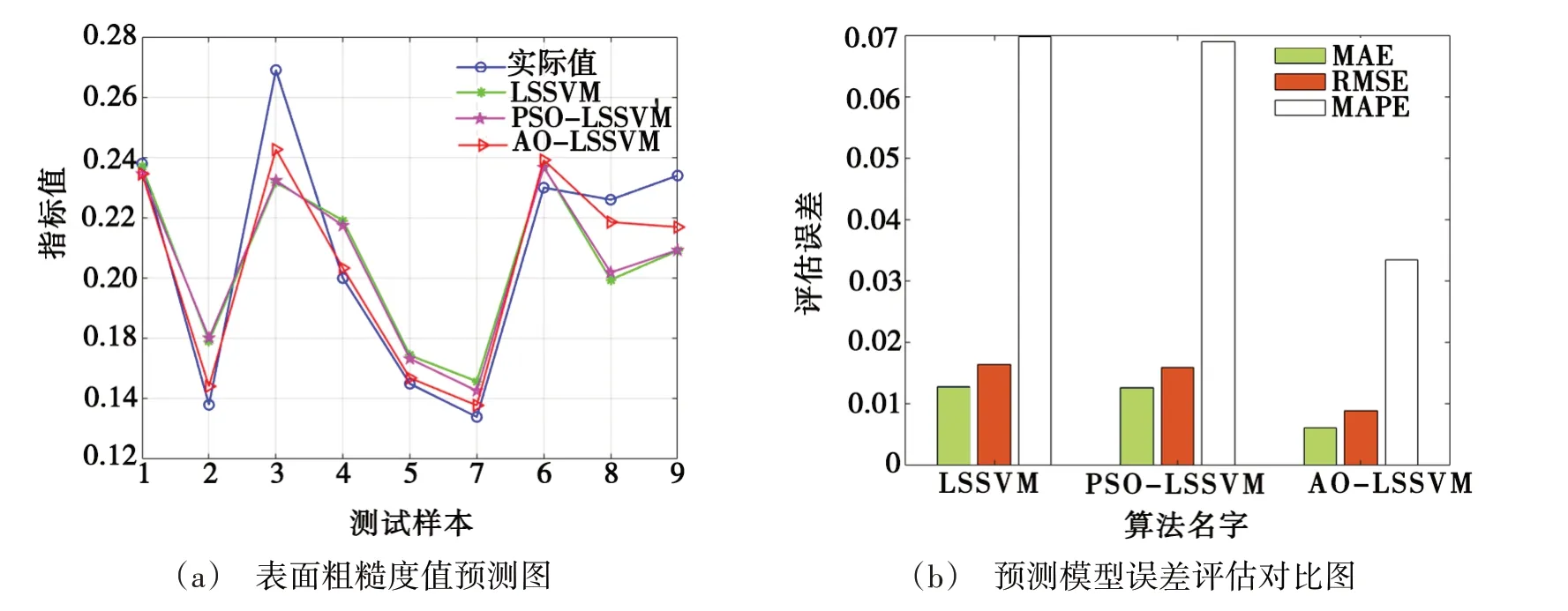
图6 AO-LSSVM、PSO-LSSVM、LSSVM测试集性能评估图Fig.6 AO-LSSVM,PSO-LSSVM,LSSVM test set performance evaluation diagram
由图5(a)和图6(a)可知,除去个别数据噪声的影响,大部分样本的预测值和真实值都较为接近。相较于PSO-LSSVM 和LSSVM,AO-LSSVM 的训练集和测试集预测结果更接近于实际测量值。由图5(b)图6(b)和表4 可知,AO-LSSVM 模型的三种性能评价指标(MAE、RMSE、MAPE)均低于PSO-LSSVM 和LSSVM 预测模型。其中AO-LSSVM 模型的MAPE 比PSO-LSSVM 模型的降低了4.682 8%,并且有较高的拟合优度(0.938 64),且接近于1,这表明AOLSSVM 的拟合程度较好,预测精度更高。综上所述,AO 优化器算法能够提高LSSVM 模型Ra的预测效果和稳定性。因此,本研究中采用AO-LSSVM 算法建立铣削铝合金Ra预测模型具有较大的优势和合理性。
4 基于AO-LSSVM 的表面粗糙度预测应用系统
为了降低预测模型的测试成本和便于实际应用,采用较优的AO-LSSVM 算法预测模型作为核心,在MATLAB 开发环境中运用GUI 界面图形设计构建铣削铝合金Ra预测应用系统,该系统操作简单、预测精度高。系统的GUI界面设计结构如图7所示,该应用系统的测试集Ra预测精度达到了95.7124%,满足实际工程需要。该应用系统包括4 个方面:数据导入;预测结果显示;Ra与切削参数的交互作用关系绘制;算法收敛性显示与切削参数选取和预测,该系统通过模块1 导入Excle 文件数据进行预测模型训练,模块2 进行预测模型验证,模块4 通过输入4 个铣削参数值进行Ra值预测。由于在实际工程应用中,不同产品对Ra的要求不同导致切削参数的不确定性,本系统通过建模和优化算法寻优,能够求解最佳的粗糙度对应的切削参数,为实际加工提供一定的参考。
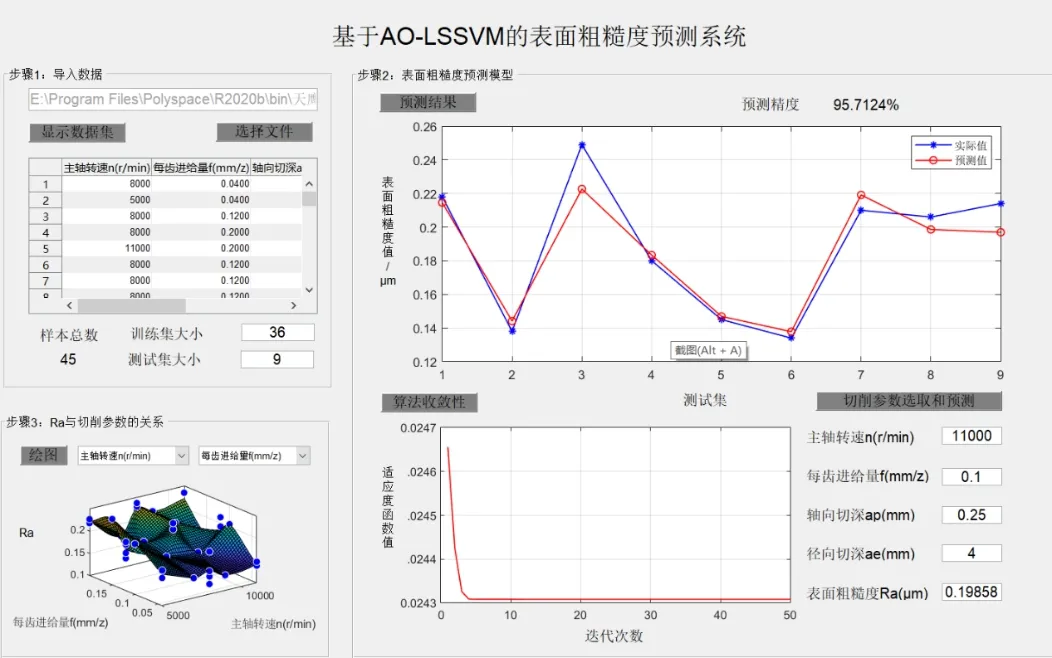
图7 表面粗糙度预测系统界面图Fig.7 Surface roughness prediction system interface diagram
Ra与切削参数之间交互关系如图8所示,由于有一部分数据为正交实验数据造成曲面图有较多的转折点,相较于其他3种切削参数,Ra与f呈现强正相关关系,这与2.2中灰色关联分析结果一致。

图8 Ra与4个铣削参数的响应曲面图Fig.8 Response surface of Ra with 4 milling parameters
5 结论
(1)本文提出一种基于AO优化器改进LSSVM算法的铣削铝合金Ra预测模型,通过与PSO-LSSVM 和LSSVM 预测模型对比分析,预测结果表明AOLSSVM 的预测精度和拟合优度均高于另外两种算法(AO-LSSVM 的预测精度和拟合优度分别为95.7124%和0.93846),故AO-LSSVM 模型在铝合金Ra预测中具有明显优势。
(2)基于GUI 搭建铣削铝合金Ra预测应用系统,该系统与AO-LSSVM 预测模型预测效果一致,通过切削参数选取能快速、便捷、准确地预测Ra值,为实际工程应用提供一定的参考。
