初中物理学生解题思维及技巧的培养

杨莉

【摘要】只有学生拥有解题思维、技巧之后，才能灵活应对各种难题，在短时间内完成题目分析，找到正确的解题思路.文章就此围绕着培养学生解题思维、技巧展开了分析和研究.

【关键词】初中物理；解题思维；解题技巧

1 各种题型的解题方法

第一，在选择题的解题中，一定要注意关键词.比如匀速直线、静止、错误的等等.这些关键信息不能看错，以免选错选项.另外，一定要完全读懂了题目再做题，不要一目十行，在题干信息尚未看清时就开始做题，完全不知道题干给了什么信息，题目所求什么信息.

第二，在填空题的解决中也要注意关键词，尤其是要注意空格后括号内的关键词，是变大变小还是增大、减小，是大于、等于或小于.如果带单位一定要在填写时填写上单位.比如重力是____N，还是重力是____.前一个填空不需要带单位，后一个要带上单位.

第三，在作图题解答中，一定要注意实线、虚线、箭头、直角符号.比如在力学题目的作图中，重点关注重力、弹力、外力、摩擦力的大小和方向.在滑轮题的作图中，重点关注力符号、箭头方向；在杠杆题目中，重点关注动力阻力方向及长度；在电学作图中，重点关注线与线之间的黑点，电学元件的顺序［1］.

第四，在解析题目中要注意一定要弄清楚已知量、未知量之间的关系，然后具体情况具体分析，注意控制变量描述条件，以此列出准确的计算式.

第五，在实验题中，学生一定要重点关注题干信息，明确实验类型、内容、要求、目的及其涉及到的物理原理等知识，以便能准确解答.总而言之，针对不同的题型，学生在解题时一定要不同的解题要点，避免不要出现遗漏、误用等信息.

2 初中物理解题技巧分析

2.1 假设法

从哲学角度来看，世间的事物都是相互联系的，且相互制约.物理规律也体现了这一点.比如在物理现象中，若某个条件改变，相应的物理现象就会改变或者物理条件出现改变［2］.此时，就会出现矛盾.而矛盾是事物发展的动力.这时就可以从矛盾发展观察、分析事物发展趋势，并假设事物发展过程中会出现什么状态、矛盾.可以说，假设思维是物理学的基本思维，在物理解题中也可以应用这种方法.

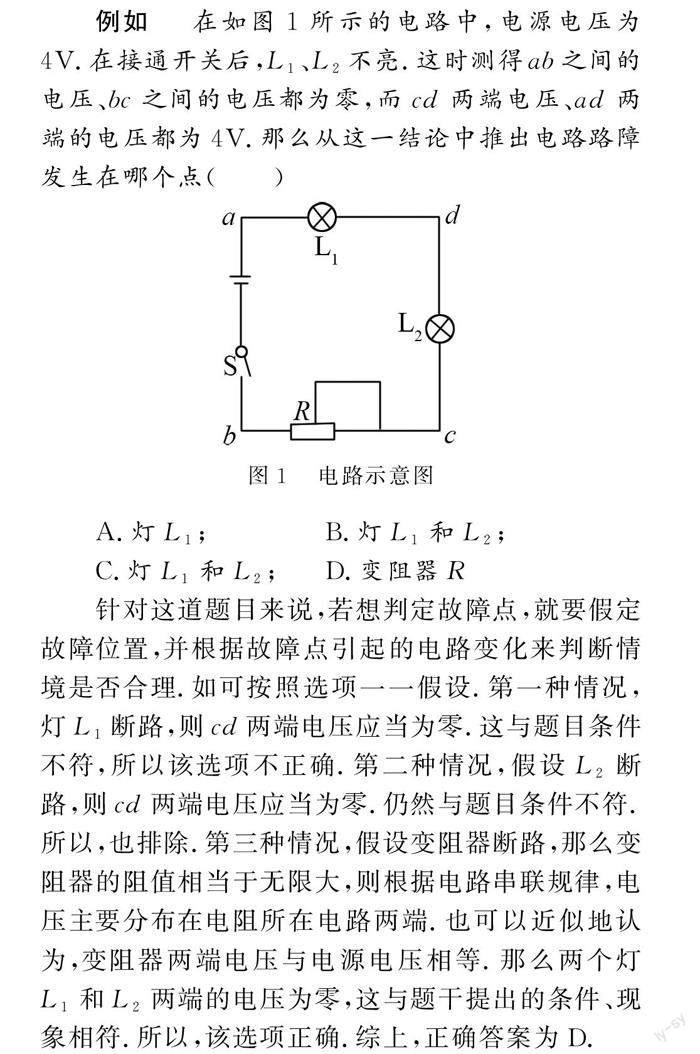
例如 在如图1所示的电路中，电源电压为4V.在接通开关后，L1、L2不亮.这时测得ab之间的电压、bc之间的电压都为零，而cd两端电压、ad两端的电压都为4V.那么从这一结论中推出电路路障发生在哪个点（  ）

A.灯L1；    B.灯L1和L2；

C.灯L1和L2；D.变阻器R

针对这道题目来说，若想判定故障点，就要假定故障位置，并根据故障点引起的电路变化来判断情境是否合理.如可按照选项一一假设.第一种情况，灯L1断路，则cd两端电压应当为零.这与题目条件不符，所以该选项不正确.第二种情况，假设L2断路，则cd两端电压应当为零.仍然与题目条件不符.所以，也排除.第三种情况，假设变阻器断路，那么变阻器的阻值相当于无限大，则根据电路串联规律，电压主要分布在电阻所在电路两端.也可以近似地认为，变阻器两端电压与电源电压相等.那么两个灯L1和L2两端的电压为零，这与题干提出的条件、现象相符.所以，该选项正确.综上，正确答案为D.

2.2 数学推导法

数学推导法是指根据题干已知条件，结合已学物理知识，找到未知条件、已知条件之间的逻辑关系，并准确列出计算式，完成推导、计算.

例如 如图2所示，用平行于斜面的力F，将重力为G的物体沿着长度为L的，高为h的斜面匀速拉到斜面顶端.这时物体所受摩擦力为f，试求f的表达式.

根据题干信息，可知重力所做的功不难求解，有用功的表达式W有用=FGS，重力做功FG=mgh，W额=fs，就可以列出其表达式：W总=W有用+W额，进而可推导出W额=W总-W有用，那么斜面的机械效率为η=W有用/W总，式子联立可得到f=FG（1-η）.从这道题目的解析中能够看出学生推导、判断时，应充分根据题干信息，理清有用功功、额外功、总功之间的关系，并结合所学知识功的计算同时、重力、摩擦力等知识筛选出有用的信息，加以运用，列出计算式，进行数学预算，直至得到最终结果.

2.3 极值法

当某个系统处于平衡状态，其中一个或几个量发生变化后，该平衡状态可能会发生变化.如果难以用常规方法解决问题，就可以选择极值法.将某个值推导最大或最小，之后再在极值情况下进行系统分析，找出已知与未知量之间的关系，最终判断出正确选项.

例如 如图3所示，一杠杆在两个力F1、F2的作用下保持平衡，如果按照下列方法进行调整，那么杠杆应当发生怎样的变化：①力F1、F2的作用点分别移项支点相同的距离；②力F1、F2作用分别远离支点同样的距离；③力F1、F2同时缩小等量的力；④力F1、F2同时增大等量的力.

首先，根据题干信息可知，原有的杠杆在保持水平.那么根据杠杆平衡原理，左右两边的力矩与力臂乘积应相等.即F1l1=F2l2.从图中可以看出l1<l2，那么可得到F1>F2，接下来，就可以用极值法解决下列四个问题.针对问题①，假设两个力同时向支点移动相同的距离为d ，那么左右两边的力矩与力臂乘积变为：F1（l1-d）、F2（l2-d）.显然，无法判断这两个值是否相等，杠杆是否仍能保持平衡，是否发生运动.所以，我们要用极限法，假设它们所移动的距离为l1，这时F1的力臂为零，且乘积也为零.而此时的F2力臂不为零，乘积也不为零.那么可知左端力矩与力臂乘积必小于右端，杠杆左端会往上翘，右端则会往下降.针对问题②，这时就可以按照解决问题①的思路解决问题②，直接运用极限法，认为远离支点的距离为很大，可以近似地忽略l1、l2.这时因为F1>F2，所以F1与力臂的乘积要大于F2其力臂的乘积.则右端会上升，左端会下降.针对问题③，仍可采用极限法解决.假设两边减小的力为F2，则此时右端的力为零，那么力与力矩的乘积也为零.则左端力与力矩乘积一定大于右端，这时杠杆左端会下降，右端会上翘.针对问题④，可假设同时增加的力为无限大，那么两边力可近似地认为相等.又l1<l2，所以左端力与力矩的乘积会小于右端的力矩与力的乘积，那么杠杆右端会下降，左端会上升.从这道题目的解析中能够看出，应用极限法解决问题还是非常简单.但需要注意的是学生一定要准确找到分析对象，合理假设无限大或无限小的情境，保证所创设情境能有效解决题干所提出的问题.

2.4 函数法解题

物理、数学同属于理工科，许多方法、思路都比较类似.比如极限法、公式法、函数法，在物理、数学解题中都有所应用.

应用函数解决物理问题，可以降低学生思维难题，提升学生的解题效率.尤其是可以缩短解题时间，保证解题质量.另外，函数不仅仅可应用在物态变化解题中，还可以应用在电路、运动学等题目的解题中.所以，学生要多练多总结，充分了解函数解题法的优缺点、适用范围，并熟练掌握函数解题法的应用技巧，以便在后续解题中能随时调用.

3 结语

总而言之，提高学生解题能力的关键是加大学生解题思维的培养力度，使其形成稳固的思维意识，在解题中能自主运用所学、常见解题思路，快速完成解題.另外，考虑到初中物理学科知识的理论性、抽象性，教师应建立长效机制，持续强化学生解题思维、能力的培养，使其逐渐吸收、内化各种方法，最终实现解题能力的提升.

参考文献：

［1］李晓红.初中物理教学中学生解题能力的培养策略［J］.数理天地（初中版），2023（10）：37-39.

［2］徐静然.初中物理课堂中图形结合解题方法的运用［J］.数理天地（初中版），2023（10）：21-22.