大气环境监测卫星地方时控制策略优化
2023-07-17石新宇马晶晶袁金如赵力文
石新宇,温 渊,马晶晶,张 娟,袁金如,赵力文,鹿 光,杜 甜
(1.上海卫星工程研究所,上海 201109;2.西安卫星测控中心,西安 710043)
0 引言
大气环境监测卫星是我国大气环境监测领域的重要组成部分,卫星装载了大气探测激光雷达(Aerosol and Carbon Dioxide Detection Lidar,ACDL)等多类有效载荷,通过主动手段与被动手段结合,实现对大气细颗粒物、温室气体、云和气溶胶等大气环境要素进行全天时综合监测。
作为一颗包含大量被动光学仪器的卫星,星上的光学载荷要求地面目标的光照条件稳定,同时要求遥感仪器每天在相同的光照条件下获取相应地区的观测资料。因此,大气环境监测卫星选择了太阳同步轨道(Sun-Synchronous Orbit,SSO)。
升交点地方时作为SSO 的重要轨道参数,对卫星运行有着至关重要的影响,其决定了卫星每天观测相同纬度地区的时间,另一方面,也决定了载荷的设计,包括探测器选用、定标方式等。卫星在轨运行期间的一个重要轨控任务即维持卫星的地方时在一个可接受的范围内,以避免卫星上的各类仪器如星敏等工作受到影响[1-2]。
1 地方时控制模型
1.1 地方时漂移估算模型
SSO 通过对升交点赤经的大小和变化速率进行设计来控制卫星轨道面与日地连线的夹角从而控制卫星的地方时。其中,升交点赤经的大小由发射窗口决定,升交点赤经的变化速率则由地球引力摄动决定。对于近地卫星,主要影响升交点赤经变化率的为地球带谐项J2的摄动。卫星升交点赤经的变化率ΔΩ可以表示为[3-4]
式中:n为卫星的平均运行角速度;Re为地球赤道半径;e为卫星偏心率;a为卫星半长轴;i为卫星倾角。
SSO 为近圆轨道,偏心率可以视为0,将J2项带入,式(1)可以简化为
当ΔΩ与地球绕日公转的平均运动角速度相同时,即可实现太阳同步特性,反之,则会引起地方时漂移。
程卫强等[5]通过对处于自由运动状态的风云一号C 星的在轨数据分析,指出通过对式(2)进行全微分,并带入式(3)即可以得到地方时漂移关于倾角、轨道半长轴及其变化率的近似计算公式:
式中:Δi0、Δa0分别为初始倾角偏置量和初始半长轴偏置量;Δi1、Δa1分别为倾角和半长轴的变化率。
对于大气环境监测卫星,入轨并完成初期飞控任务后即进入了标称设计轨道,随后的长期管理中,轨道高度由地面实时监测并进行精确控制,因此,式(4)中轨道高度偏置量Δa0及变化率Δa1均可以置0。同时,将tani项在初始倾角i0处进行泰勒展开,取一次项以提高计算精度。整理后卫星地方时漂移量可以写为关于入轨倾角偏置量和倾角变化速率的关系如下:
式中:ΔTd0为入轨时地方时的偏置量。
1.2 地方时漂移控制方法
SSO 卫星地方时由升交点赤经决定。根据卫星轨道动力学,升交点赤经由卫星轨道面与赤道面的交点确定。考虑卫星绕地球旋转的巨大角动量,直接通过轨控控制升交点赤经需要消耗大量的燃料。因此,对于SSO 卫星,在确保卫星在正确的发射窗口发射以获取一个正确的升交点赤经初值后,主要通过调整倾角来控制寿命中的地方时漂移[6-7]。当卫星倾角大于式(2)确定的同步条件时,卫星升交点赤经的变化率增大,卫星地方时逐渐朝正方向漂移;反之则卫星地方时朝负方向漂移[8]。
由于卫星运行时受月球的三体引力摄动影响,在卫星处于某个地方时时,其倾角漂移速率Δi1长期看是恒定的,故式(5)中只有倾角偏置量Δi0和地方时偏置量ΔTd0可以直接控制。由于倾角偏置量是相对于标称倾角而言的,对于确定轨道高度的SSO,标称倾角是固定的,因此进行倾角控制时相当于改变了倾角偏置量。
根据上述分析,大气环境监测卫星的地方时漂移控制问题即转化为如何综合选择地方时偏置量、初始倾角偏置量、控制日期、倾角控制量4 个参数来使得卫星整个寿命周期内的地方时漂移最优。
1.3 地方时控制优化模型
上节分析说明了由于倾角摄动存在使得卫星不可能始终保持在标称的倾角上,因此,卫星寿命周期内需要进行数次倾角控制来保证卫星的地方时漂移在可控范围内[9]。根据工程经验,8 a 寿命的SSO 卫星可以通过地方时初期偏置外加寿命周期内的一次倾角控制来保证地方时漂移在20 min以内。
评价地方时控制效果的最重要指标为地方时漂移量。由于正偏负偏均对卫星观测效能造成影响,设计时地方时的实际值和设计值偏差尽可能小,因此,效果评价时以相对标称值的漂移量即地方时偏差作为评价指标。
大气环境监测卫星的设计寿命是8 a,在考虑寿命期内长期控制的情况下,有2 种评价控制策略的方式:①以寿命内的平均地方时偏差作为评价指标;② 以寿命内的最大地方时偏差作为指标。根据式(3)可以看出,地方时偏差近似为一抛物线。若选用平均地方时偏差作为指标,可以预见由于抛物线顶点附近地方时变化较缓慢,对平均值的权重较大,因此优化结果会形成顶点附近偏差小、两侧偏差大的情况。而工程实践中,地方时偏差往往以“偏差不超过XX 分钟”形式提出,因此对于大气环境监测卫星,采用寿命内最大值的作为评价指标较为合适,即
式中:P为地方时控制评价指标。
由式(6)可以看到,该函数为多参数非线性函数,具体的表达式需要分段讨论,较难通过解析手段找到最大值。因此,下面采用较常用的遗传算法寻找其全局最小值来实现对控制策略的优化。
2 遗传算法的编码方式和参数选择
遗传算法模拟了自然界生物受自然选择压力进化的过程。表现在算法上即通过交叉、变异方法探索整个解空间,通过人为施加的选择压力不断挑选出更加符合问题要求的解来实现问题的全局优化。
遗传算法的使用需要确定一些算法参数,包括适应度函数、基因编码方式、选择算子、交叉算子、变异算子和种群规模等。下面针对问题进行确定。
1)适应度函数用于评价个体的质量,高适应度的个体表明解更符合优化的方向。本问题中,地方时最大偏差量越小越好,故适应度函数可以直接取最大偏差量的倒数,
式中:F为适应度。
2)遗传算法最常用的基因编码方式为二进制编码,即将解空间映射为具有一定步长的二进制串。该方法的好处是处理简单,但最大问题在于解空间是离散的。对于本问题而言,多个参数的取值范围都是连续的,故本问题不适用二进制编码,需要直接使用实数编码方法,即直接使用优化参数的实数值作为基因。
3)选择算子用于在已有种群按一定条件挑选存活个体,是施加选择压力的步骤。通常做法是根据适应度选择,适应度越大的个体被选中(存活)的概率越高。但是观察本问题的适应度函数后可以发现,在进化一段时间后,可以预期由参数改变带来的地方时偏差量不会变化很大,取倒数后的适应度函数值变化会更小。因此如果直接采用适应度作为选择依据,在优化进行一段时间后,算法将退化为随机选择。JADAAN 等[10-14]分别对多种选择算子进行了比较,结果表明,除了直接使用适应度作为选择依据外,可以采用适应度排名作为选择的依据,即适应度排名越靠前的个体被选择的概率越大,该方法可以有效放大适应度接近的个体。一个由10 个个体组成的种群的最大地方时偏差和以式(6)计算得到的适应度的结果见表1。直接使用式(6)计算的适应度和使用适应度排名情况下种群各个体的存活概率如图1 所示。可以看到,在种群内部最大的地方时偏差差值约为0.5 min 的情况下,使用适应度排名方法进行选择可以有效拉开优秀个体和不合格个体的适应度差距。

图1 适应度和使用适应度排名情况Fig.1 Ranking of the fitness and usage fitness

表1 相同适应度在2 种选择算子下的存活概率Tab.1 Survive probabilities of the same fitness under two selection operators
4)交叉算子用于产生下一代的种群,DEB 等[15]提出了一种适用于实数编码的模拟二进制交叉算子,可以实现与二进制交叉类似的性能,为实数编码的常用交叉算子,泛用性广,本问题直接使用该交叉算子。该算子具体表达如下:
式中:u∈[0,1)为一随机数;n为分布参数,默认取1;p1、p2为两个父代;c1、c2为两个子代。
4)变异算子用于模拟进化时的基因变异,是遗传算法跳出局部最优解的重要手段,实数编码下常用的变异算子为多项式变异算子[16]:
式中:u∈[0,1)为一随机数;U、L为取值的上下界;ηm为分布指数;c为变异前的个体。
5)在种群规模方面,采用适应度排名的选择算子,种群规模不宜过小,过小可能将放大适应度的差异,使无法跳出局部最优解。HASSANAT 等[17]指出,对于并不十分大的搜索空间,使用包含数10 个个体的种群即可很好进行搜索,因此本问题使用1 个包含60 个个体的种群。
3 地方时控制优化结果
设置进化代数150 代,得到优化结果见表2,最优策略下的地方时漂移曲线如图2 所示,最大地方时偏差量的代际变化如图3 所示。通过遗传算法优化,将寿命内地方时偏差量的最大值从最初的11 min 降低到了6.6 min。
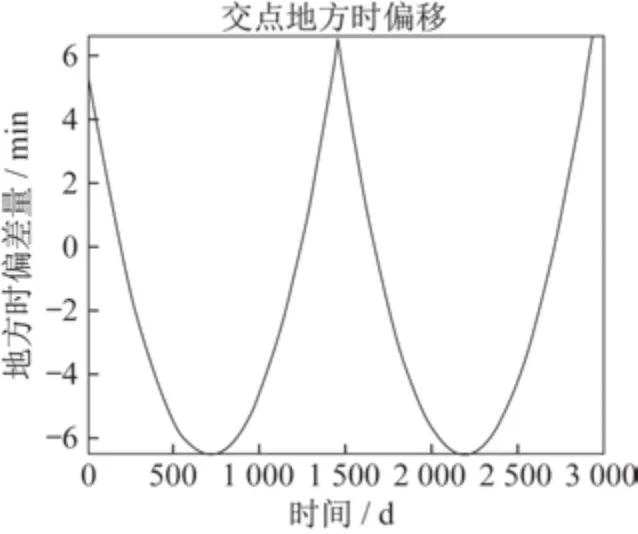
图2 最优策略下的地方时漂移曲线Fig.2 LTAN deviation curve under the optimization strategy
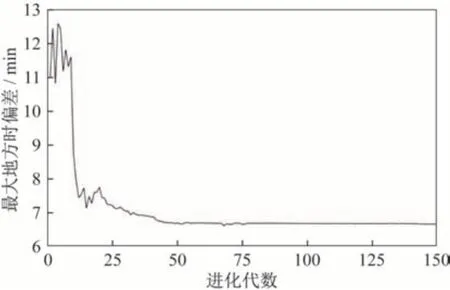
图3 代际进化曲线Fig.3 Evolution curve

表2 优化结果Tab.2 Optimization results
4 燃料受限情况下的最优控制曲线
上章优化结果中,控制量的大小并没有做出限制,而控制量的大小直接与消耗的燃料成正比。在实际工程实践中,可以用于进行倾角控制的燃料往往是受到限制的。卫星早期设计时,更希望获得在某个给定的燃料消耗的情况下能实现的最优地方时控制结果;反之,在给定最大地方时偏差下,获取所需的最小燃料消耗也是设计中经常使用的,因此,需要计算倾角控制量与地方时偏差间的最优控制曲线。
在之前的分析中,控制量并未受到限制,为无约束情况下的最优控制结果。根据本章的分析目标,通过限制控制量,可以得到一次控制情况下最优地方时偏差关于最大倾角控制量的曲线,如图4所示。对于2 次或更多次控制的最优曲线,可以通过改写适应度函数获得。根据该曲线,为了保证地方时偏差15 min 以内,在不考虑入轨偏差和控制偏差的情况下,应至少分配0.07°的倾角控制量所需的燃料。
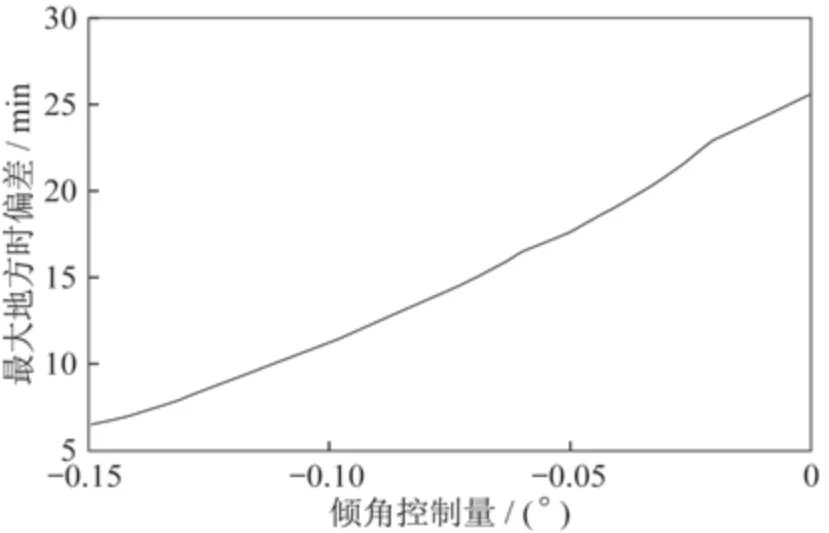
图4 最优控制曲线Fig.4 Optimal control curve
5 结束语
本文建立了地方时漂移估计,通过倾角的地方时漂移控制方法及地方时控制优化模型,然后通过遗传算法优化给出了参数不限情况下的一次地方时控制的最优控制策略,最后探讨了在倾角控制量受限情况下一次地方时控制所能达到的最优结果。优化结果表明,大气环境监测卫星通过一次倾角控制能实现的最优地方时控制偏差约为6.6 min,而为了保证15 min 的地方时偏差,需要分配的燃料应至少可以对卫星进行0.07°的倾角控制。两项分析结论均已应用于大气环境卫星的在轨地方时控制,对其他SSO 的地方时控制策略制定也有积极的参考意义。
