基于LSTM-KF的非共视情况下舰船目标跟踪

郭立民,郑鑫桐,马思达

(哈尔滨工程大学,黑龙江 哈尔滨 150001)

0 引 言

随着科技的发展,电子战已经成为现代战争最重要的方式之一,而对敌方雷达进行定位跟踪是其中重要的一个部分。

雷达定位[1]可以按照观测站数量分为单站定位与多站定位2种。多站定位由于精度高成为常用的定位手段。但是在实际定位跟踪环境中,非共视情况的发生会使多个观测站无法同时检测到雷达信号,导致目标位置或轨迹的确定存在误差或者无法准确估计的情况出现[2-5]。造成多个观测不能同时检测到辐射源信号的原因有很多,主要包括:(1)观测站的灵敏度只能收到主瓣信号,而无法检测到辐射源的副瓣;(2)观测站之间距离过大,导致观测站接收不到信号的情况出现;(3)存在障碍物遮挡导致信号无法正常传播。

在多岛礁海域中对舰船雷达进行定位跟踪时[6],常因遮挡造成信号无法正常接收。对雷达目标定位跟踪时,目标就处于“非共视状态”。本文基于该情况下的非共视现象进行研究。

针对目标处于非共视的情况,无源滤波跟踪是一个非常重要的方面。卡尔曼滤波算法自上世纪被首次提出后,在目标跟踪领域广泛应用,至今仍有许多学者在对它进行研究。虽然卡尔曼滤波算法在目标运动状态较为单一的情况下有着较好的跟踪效果,但面对机动目标,由于目标轨迹复杂等原因,其跟踪性能会有所下降。大量的研究学者对该问题进行了研究。2019年,任宇翔等人将LSTM网络应用到船舶航行动态预测领域[7];2020年,大连海事大学的王研婷将CNN和LSTM相结合对船舶轨迹进行预测[8];2021年,徐洪敏将LSTM网络模型应用在船舶航行轨迹预测中[9];同年,吴鹏程、罗亮等人基于RNN-LSTM对船舶运动轨迹进行预测[10]。本文通过深入研究,将其应用在舰船运行过程中的非共视情况下,提高了非共视情况下舰船目标的定位精度,有效降低了舰船航行过程中轨迹跳变情况的发生。

1 非共视场景描述

以某海域某一岛礁为例,其东北-西南长约3 000 m,某舰艇航速约14.5～15.5 m/s,若自东北至西南方向以匀速直线航行,完全通过该岛礁约需200 s时间。

若同时有3个静止观测站对岛礁附近航行中的舰艇进行勘测定位,假设舰艇自西向东经过该岛礁,其运动轨迹模拟情况如图1所示。

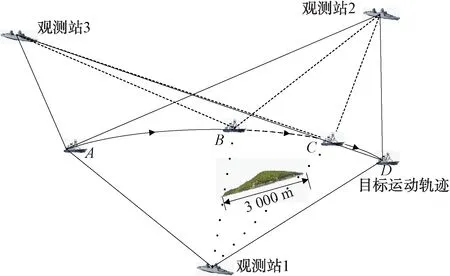
图1 非共视场景详细示意图

在该目标运动轨迹上取4个状态点,分别为轨迹起点A、非共视状态起点B、非共视状态终点C、轨迹终点D。

在A点时,3个观测站均能接收到目标信号,如图中实线所示;目标运动到B处和C处之间时,由于岛礁的遮挡,无法使得3个观测站同时收到目标信号,时差信息无法单独起到定位作用。当观测站数量为2个时,可以与测角信息联合对目标状态进行跟踪,但是跟踪精度会降低,非共视情况下可正常接收信号的观测站与目标之间如图中半划线所示,同时无法接收信号的情况如图中双点线所示;当舰船继续行驶,离开C点即离开岛屿遮挡范围直至运动到D点的过程,可正常进行时差定位。有效观测站个数的变化与观测范围、障碍物大小、运动轨迹均有关。本文主要针对示意图中舰船运动至B、C两点之间场景进行研究。

在非共视条件下,可以考虑采用卡尔曼滤波(KF)算法,但由于KF算法在机动目标应用中的局限性,本文考虑将LSTM神经网络和KF算法相结合进行机动目标的定位跟踪,并对其进行仿真验证。

2 相关算法

2.1 卡尔曼滤波算法

卡尔曼滤波算法的基本过程包括估计与预测2个步骤,其基本思想是利用前一时刻的结果和当前时刻的观测值来更新状态变量的估计,求出当前时刻的估计值[11]。

首先假设系统的状态方程为:

Xk=f(Xk-1)+wk-1

(1)

Yk=h(Xk)+vk

(2)

式中:f为状态转移函数;h为量测模型函数;Xk表示k时刻的状态向量;Yk表示k时刻的量测向量;wk～N(0,Qk)为过程噪声;vk～N(0,Rk)为量测噪声,二者互不相关。

通过已知目标运动轨迹得到k-1时刻目标状态为Xk-1。

根据状态转移函数得到k时刻的状态预测值:

(3)

此时的预测误差协方差矩阵可以表示为:

(4)

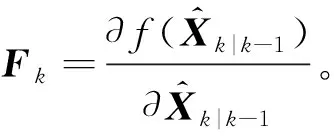
Pk-1为k-1时刻的估计误差协方差矩阵。更新估计误差的协方差矩阵,可以简化为:

Pk=(I-KkHk)Pk|k-1

(5)

第3步得到k时刻状态预测值,由此可以得到k时刻的量测信息预测值为:

(6)

最后,结合k时刻的量测数据Yk,估计k时刻状态Xk的递推形式为:

(7)

式中:Kk称为卡尔曼增益,是k时刻对新息的加权,反映了状态估计过程中对新息的重视程度,卡尔曼滤波增益公式为:

(8)

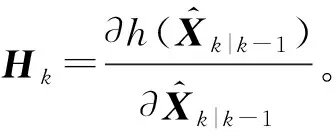
2.2 LSTM神经网络

循环神经网络(RNN)是一种用于处理序列数据的神经网络。相比一般的神经网络来说,能够处理序列变化的数据。LSTM是一种特殊的RNN,主要是解决长序列训练过程中的梯度消失和梯度爆炸问题。简单来说,就是相比普通的RNN,LSTM能够在更长的序列中有更好的表现。LSTM神经网络模型结构图如图2所示。

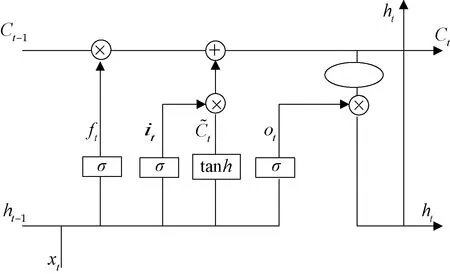
图2 LSTM神经网络模型结构图

LSTM内部主要有3个门:

(1) 忘记门。通过忘记门对上一个节点的输入进行选择性忘记。该忘记门会读取上一个输出ht-1和当前输入xt,做一个Sigmoid的非线性映射,然后输出一个向量ft(该向量每一个维度的值都在0到1之间,1表示完全保留,0表示完全舍弃):

ft=σ(Wf·[ht-1,xt]+bf)

(9)

式中:σ为Sigmoid激活函数。

(2) 输入门。一共包含2个部分:一是决定什么值将要更新;二是创建一个新的候选值向量:

it=σ(Wi·[ht-1,xt]+bi)

(10)

(11)

(12)

(3) 输出门。通过将细胞状态以及输出比例相乘,输出得到该LSTM神经元最终的输出值:

ot=σ(Wo·[ht-1,xt]+bo)

(13)

ht=ot·tanh(Ctt)

(14)

2.3 算法模型

在本文中,将卡尔曼滤波算法和LSTM神经网络相结合,以LSTM神经网络对舰船运动轨迹的预测值作为卡尔曼滤波中的状态预测值,其模型流程如图3所示。

本文将目标位置坐标作为网络模型的输入,取70%的数据点作为网络模型的训练数据,剩下30%的数据点作为模型的测试数据,隐层神经元个数为20,输入延时为5。LSTM神经网络参数示意图如图4所示。

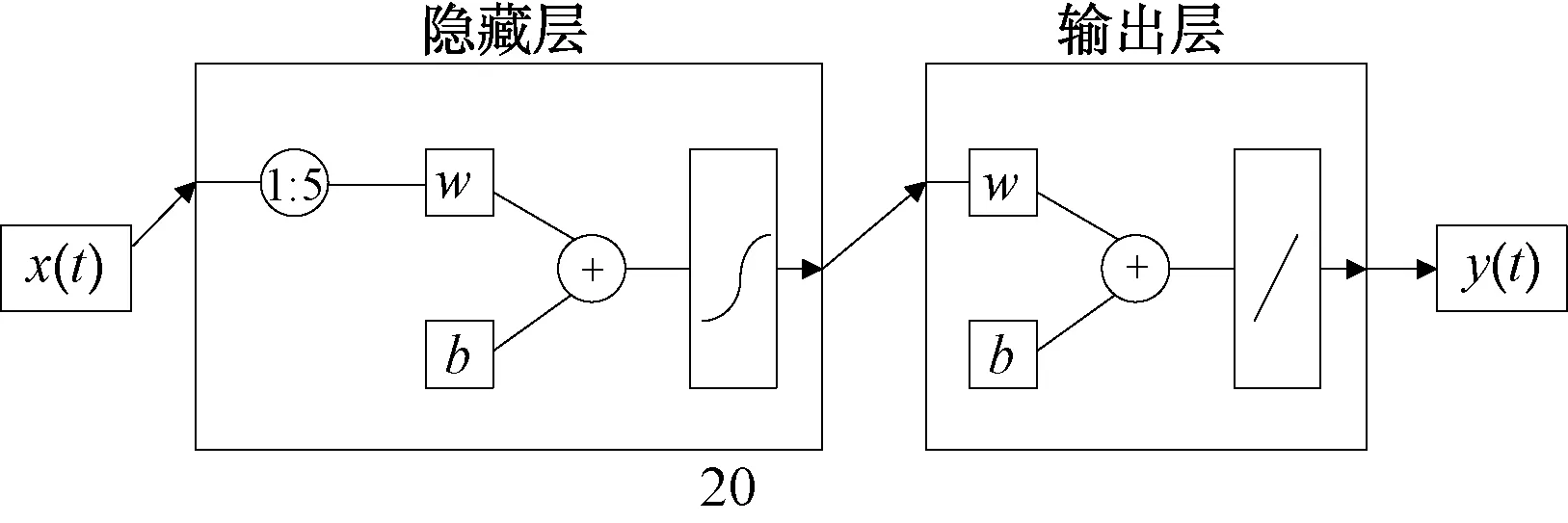
图4 LSTM神经网络参数示意图

3 实验及结果分析

为验证本文所提出算法的有效性,假定通过3个观测站对海面运动目标进行观测,3个观测站坐标分别为SA(0,0)、SB(18,22.8)、SC(-16.4,24)(单位:km),定义定位误差为定位位置与理论位置的距离差。

在仿真过程中,对运动目标设置非共视情况,并对处于非共视情况的目标分别进行测向定位、LSTM网络预测跟踪、LSTM-KF模型跟踪,并对3种情况下的误差进行分析。

分别对常见运动模型进行仿真,分为如下情况。

3.1 常速度(CV)模型

CV模型假设目标做匀速直线运动,其状态转移矩阵FCV为:

(15)

式中:T0为观测时间间隔。

在舰船目标航行过程中,以某舰艇航行速度15 m/s为例,观测总时间T=600 s,观测时间间隔T0=1 s,时间误差50 ns,构建目标运动模型。其理论运动轨迹如图5所示。

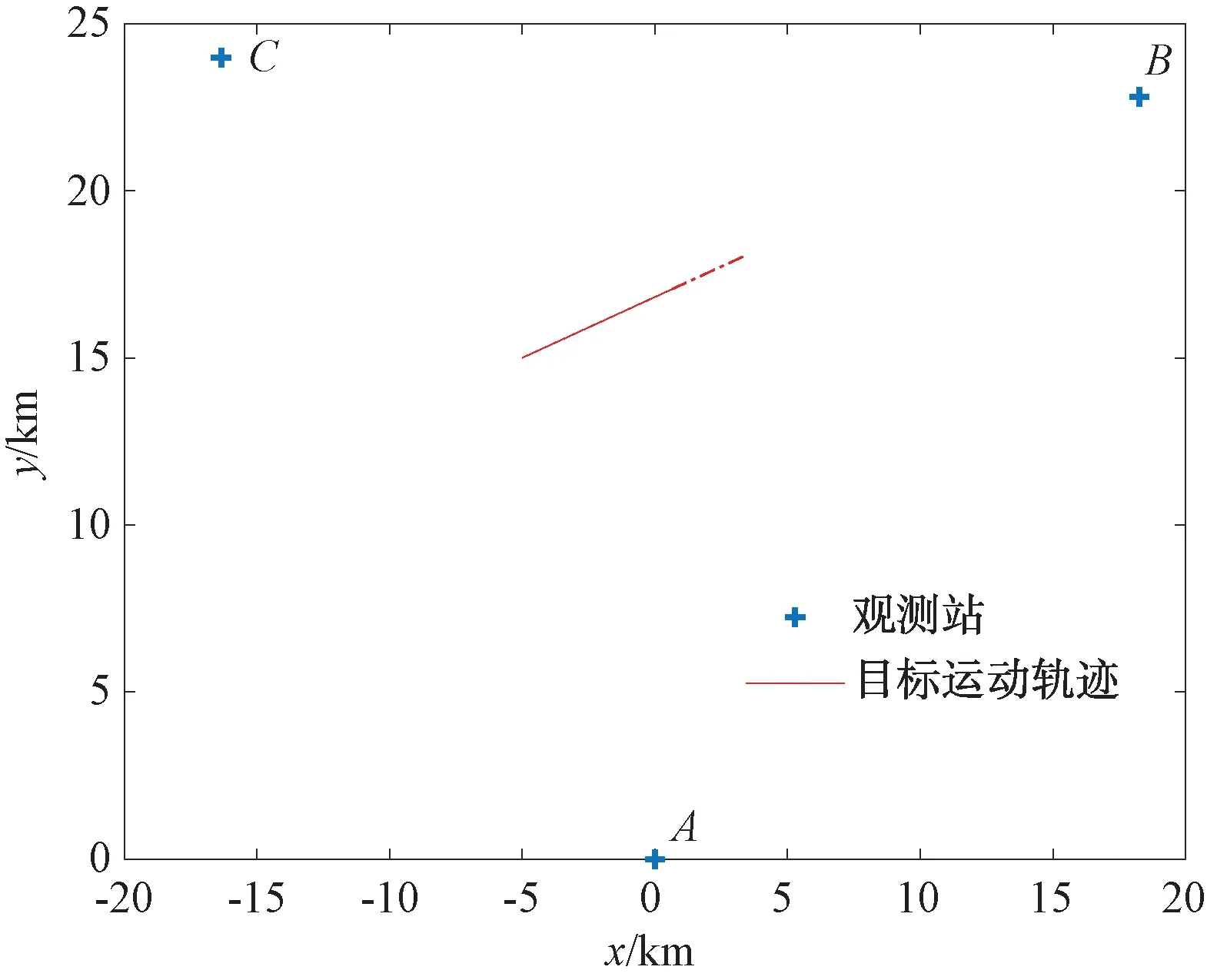
图5 机动目标运行轨迹——CV模型

表1为CV模型下3种算法平均误差对比。

表1 CV模型下3种算法平均误差对比

将运动轨迹最后200 s时间设定为非共视情况,如图中虚线所示。其仿真分析结果如图6所示。

图6 CV模型算法比较

3.2 坐标转弯(CT)模型

CT模型为匀速转弯模型,当运动角速度ω>0时,对应逆时针转弯模型;当ω<0时,对应顺时针转弯模型,其状态转移矩阵FCT为:

(16)

式中:T0为观测时间间隔。

在舰船目标航行过程中,以某舰艇航行速度15 m/s为例,观测总时间T=600 s,观测时间间隔T0=1 s,时间误差50 ns,构建目标运动模型。其理论运动轨迹如图7所示。

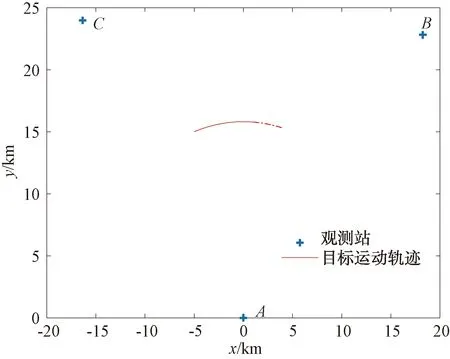
图7 机动目标运行轨迹——CT模型

将运动轨迹最后200 s时间设定为非共视情况,如图中虚线所示。其仿真分析结果如图8所示。表2为CT模型下3种算法平均误差对比。

表2 CT模型下3种算法平均误差对比

3.3 CT-CV结合模型

设置舰艇轨迹由CT模型和CV模型两部分构成,其中前200 s时间为CT模型,后200 s时间为CV模型,并取201 s～400 s期间(即2种运动模型转换区域)为非共视情况,其理论运动轨迹如图9所示,其中虚线为非共视情况。

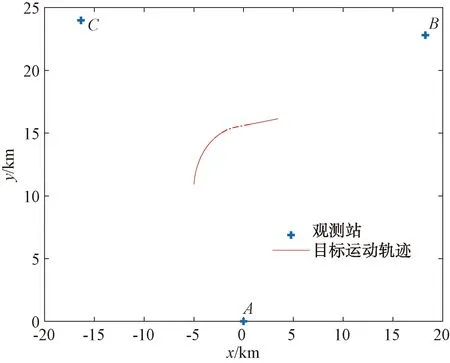
图9 机动目标运行轨迹——CT-CV模型

仿真结果如图10所示。表3为CT-CV模型下3种算法平均误差对比。

表3 CT-CV模型下3种算法平均误差对比

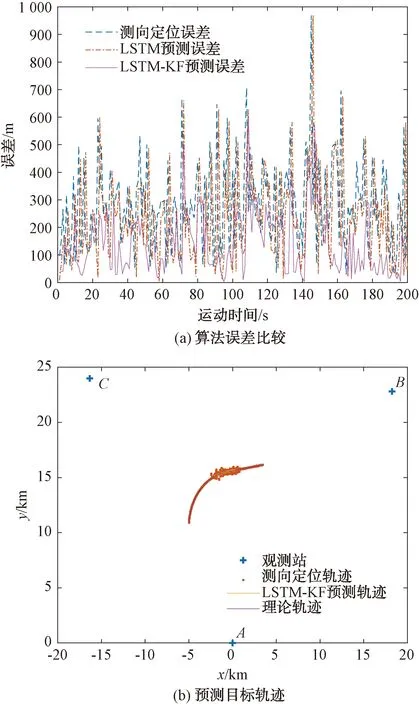
图10 CT-CV模型算法比较

4 结束语

本文提出了KF算法和LSTM神经网络相结合的LSTM-KF算法,并通过实验结果分析,对舰船运行过程中发生岛礁遮挡造成观测站无法同时接收到脉冲信号的“非共视情况”,相较于传统应用中使用测向定位进行目标定位,本文提出的算法具备更高的精度,且减少了轨迹跳变情况的发生,在真实的海战场环境中具有一定的应用意义。