基于多重多元回归的高空冰晶冰水含量估计方法

李 海 张彬蕾 孟凡旺 孙 研 韩雁飞

(1.中国民航大学天津市智能信号与图像处理重点实验室 天津 300300;2.中国航空工业集团公司雷华电子技术研究所 江苏无锡 214063;3.中国电子科技集团航空电子有限公司 成都 611731)

0 引言

当民航飞机在巡航阶段(一般在22000英尺以上)飞行时,高空冰晶是对飞机飞行安全威胁较大的危险天气现象之一。在高空冰晶聚集区域,发动机叶片表面的冰晶凝结会导致发动机失控与喘振,燃烧室熄火或发动机叶片损坏等[1]。高空冰晶极易造成机载传感器探头堵塞,使得探测数据异常,造成飞机失控[2]。近年来,高浓度冰晶导致喷气式飞机发动机动力损失的事件已经引起了发动机制造商、安全监管部门和气象研究界的广泛注意[3]。据波音公司统计,自20世纪90年代初以来,在通勤飞机和大型运输飞机中,已有超过150起飞机动力损失或发动机回滚(发动机失去控制)等不安全事件被归因于高空冰晶[4]。这些统计报告表明:高空冰晶对航空运输业和旅客飞行安全造成了严重影响。因此高空冰晶检测及危险等级区域告警成为保障航空安全的一项重要课题。高空冰晶检测及其危险级别量化通过估计雷达所探测空间的冰晶密度,即冰水含量(Ice Water Content,IWC)实现,单位为g/m3[5]。冰水含量的准确估计是检测高空冰晶的前提。

机载气象雷达是飞机探测危险气象保障飞机安全运行的重要监视设备。目前,实现冰晶冰水含量估计的方法主要是依据冰水含量与雷达反射率因子之间的经验关系。1954年,Atlas通过研究飞机实测的谱参数数据,得到雷达反射率因子-粒子分布-冰水含量之间的经验关系[6]。1992年,Liao等人探讨了Ka波段雷达和W波段雷达的冰晶冰水含量与雷达反射率因子之间的关系[7]。1995年,Brown用毫米波机载雷达探测了冰晶云,并给出了冰水含量与雷达反射率因子经验公式[9]。2004年,Matrosov研究了利用雷达反射率因子以估测海洋性层云含水量的方法,比较了在不同的降水云与非降水云强度界限时云内含水量的变化[10]。2015年,Protat给出了在35GHz和95GHz毫米波雷达下的冰水含量与雷达反射率因子统计关系[11]。上述研究分别针对不同场景下不同波段的雷达估计冰水含量时雷达反射率因子与冰水含量之间的关系进行统计分析,得出了不同情况下雷达反射率因子与冰水含量之间的经验关系。但由于每个研究人员拥有不同的数据集,所得经验关系具有较大的局限性,且仅利用雷达反射率因子对冰水含量进行估计的准确性较差,难以依据高空冰晶浓度的分布进行危险性评判及区域告警,必须寻求更精准的冰水含量估计方法。因此,开展高空冰晶冰水含量估计的研究具有非常重要的意义。2016年,美国霍尼韦尔国际公司的研究团队提出了一种机载X波段气象雷达的高空冰晶检测方法,并成功进行飞行测试[12]。该算法基于机器学习的方法,利用冰晶的雷达反射率因子、高度和温度等特征建立特征向量估计高空冰晶冰水含量,理论上能够实现冰晶检测。虽然关于该功能的数据和算法原理以及相关雷达结构等信息均未被公开,但利用可用信息实现对于冰晶冰水含量参数的预测、估计这种思想,为准确实现冰水含量估计提供了研究思路。

回归算法是常应用于气象预测、降水量估计等领域的一种以数据特征提取为基础,用数据分析的相关模型和数据挖掘技术进行处理分析,用于估计或预测未知参数的数据处理技术[13]。这种特性为回归算法应用于高空冰晶冰水含量估计提供了理论基础。目前,将回归算法应用于高空冰晶冰水含量估计的研究尚属空缺。

本文提出了一种基于多重多元回归的高空冰晶冰水含量估计方法,分析验证了将回归算法引入高空冰晶冰水含量估计的可行性。该方法将冰晶冰水含量单一的目标值估计问题转化为多重多元回归的冰水含量标记向量预测问题,利用训练好的回归模型最终实现高空冰晶的冰水含量估计。针对典型深对流区域仿真数据进行实验分析表明,该方法可有效地估计高空冰晶的冰水含量,估计结果较为准确。

1 基于多重多元回归的高空冰晶冰水含量估计

基于多重多元回归的高空冰晶冰水含量估计方法需要通过带标签的训练数据建立回归模型,建立多重多元回归模型首先需要建立训练样本的特征矩阵及标签矩阵,然后利用偏最小二乘回归(Partial Least Squares Regression,PLSR)算法建立起冰晶样本多维关键特征向量与该样本冰水含量之间的映射关系。得到训练好的多重多元回归模型后,将待测数据输入模型得到冰晶冰水含量估计结果。下面分别对建立样本特征矩阵和标签矩阵,建立多重多元回归模型以及利用回归模型完成高空冰晶冰水含量估计的过程进行介绍。

1.1 建立特征矩阵和标签矩阵

建立回归模型首先需要建立训练样本的特征矩阵及标签矩阵。建立样本特征矩阵时考虑高空冰晶的浓度分布受众多因素的影响,除雷达反射率因子外,与冰晶结冰事件相关的气象环境参数包括温度、高度、气压、空气密度和对流风暴类型等也会限制冰晶的产生[5]。从冰晶的产生条件来看,利用气象环境参数高度、温度确定冰晶可能存在的区域是可行的。因此,本文依据影响高空冰晶冰水含量的关键特征参数建立特征矩阵。除雷达反射率因子外,再引入高度、温度信息作为冰晶样本的特征,建立的特征矩阵X为

(1)

其中,特征矩阵X的每一个行向量表示一个样本的特征参数向量。假设有k个冰晶样本数据,第i个冰晶样本xi(i=1,2,…,k);有3个特征参数,表示为xi=(Zi,Hi,Ti),Z代表雷达反射率因子(单位:dBZ),H代表高度(单位:km),T代表温度(单位:℃)。

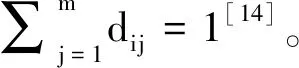
(2)

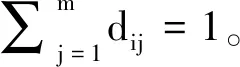
(3)

1.2 建立回归模型

在1.1节基础上,本文采用多重多元回归模型来求解由特征矩阵X到标签矩阵Y的映射问题,模型的求解目标为利用训练数据,得到冰晶样本的特征向量与真实冰水含量值之间的最优映射关系。将基于经验公式的冰水含量值计算问题转换为利用多自变量对因变量进行预测的多重多元回归分析问题,并采用偏最小二乘回归方法对冰水含量进行求解。偏最小二乘回归模型结构如图1所示。

图1 偏最小二乘回归模型结构图

偏最小二乘回归模型分别由外部模型和内部模型组成,首先由外部模型对特征矩阵X和标签矩阵Y进行成分提取,然后由内部模型建立提取出的n对成分之间的关系,最后构建特征矩阵X和标签矩阵Y的回归模型。具体过程是首先对特征矩阵X和标签矩阵Y提取第一对主成分v1和u1,然后偏最小二乘回归分别建立特征矩阵X与v1的回归方程以及标签矩阵Y与v1的回归方程。如果建立的回归方程交叉有效性验证指标小于门限值,则算法终止;否则,接下来利用特征矩阵X与v1建立回归方程产生的残差矩阵以及标签矩阵Y与u1建立回归方程产生的残差矩阵进行第2轮的成分提取。如此反复迭代,直到回归方程的交叉有效性指标达到门限值时停止迭代。若最终共提取了n个成分,则利用上述成分v1,v2,…,vn构建的X与利用上述成分v1,v2,…,vn构建的Y建立标签矩阵Y关于特征矩阵X的回归方程。以下对这一过程的原理及实现进行详细阐述。

训练样本数据含有多维自变量和多维因变量,偏最小二乘算法首先提取训练样本数据的特征矩阵X和标签矩阵Y中的第一对主成分v1和u1,其中,主成分v1和u1可以作为原始特征矩阵X和标签矩阵Y的线性变换,权重系数向量分别设为p1和q1,即v1=Xp1,u1=Yq1。为了满足回归分析的需要,应使v1和u1尽可能多地携带样本特征矩阵X和标签矩阵Y的信息,即v1和u1方差最大,且满足v1和u1相关程度达到最大,即相关性系数达到最大值,综上当v1和u1的协方差达到最大即可满足要求[13]。为了得到成分v1和u1首先需要求得p1和q1,即求解满足式(4)目标函数的p1和q1:

(4)

引入拉格朗日乘子算法可得:

(5)

分别对p1和q1求偏导,并令之为0,得:

(6)

(7)

由式(7)可知,p1是XTYYTX的最大特征值对应的单位特征向量,q1是YTXXTY最大特征值对应的单位特征向量。求得p1和q1后,即可得到成分:

(8)

求解出第一对成分v1和u1后,建立回归方程:

(9)

式(9)中,c1=XTv1/‖v1‖2;r1=YTv1/‖v1‖2是回归系数向量即投影向量;E1,F1是回归方程的残差矩阵。

(10)

(11)

(12)

(13)

(14)

继续建立回归方程为

(15)

将式(15)第二个公式带入式(9)第二个公式可得:

(16)

以此类推,不断对残差矩阵建立回归方程,对上述过程进行迭代,迭代过程中通过交叉有效性验证判断是否停止迭代,若最终对X和Y共提取了n对成分,最终可得到的回归模型为

(17)

迭代计算过程中可得:

(18)

由于式(17)中v1,v2,…,vn中任一成分vh(h=1,2,…,n)是原始特征矩阵X的线性组合[15],即

(19)

其中:

(20)

式(20)中,I为单位向量,p和c均为迭代过程中计算得到。因此可将公式(17)可转化为标签矩阵Y关于特征矩阵X的回归方程:

(21)

记为

(22)

D是偏最小二乘回归方程的回归系数向量,则有

Y=XD+Fn

(23)

其中,Fn为最终达到迭代要求时的残差矩阵,在后续使用测试数据进行冰水含量估计时可忽略[15]。

至此,针对冰晶冰水含量估计的多重多元回归模型训练完成。接下来利用训练好的回归模型对待测气象数据样本进行冰晶冰水含量估计。

1.3 高空冰晶冰水含量估计

(24)

(25)

冰晶冰水含量估计结果大于0,则说明存在冰晶,冰水含量越大说明该空域内冰晶含量越高,根据冰水含量的估计结果可判断冰晶是否存在,且冰水含量估计结果可作为后续冰晶的危险程度判决依据。

2 方法流程与实验步骤

实验数据是利用WRF(Weather Research and Forecasting,WRF)天气模拟与预报软件模拟得到的气象场景数据以及利用气象雷达回波仿真得到的雷达回波数据。仿真数据包含建立特征向量需要的雷达反射率因子,计算温度、高度信息所需要的气压、海拔高度、扰动位温等数据和计算冰水含量真值所需要的冰水混合比、空气密度等数据。多重多元回归的高空冰晶冰水含量估计方法流程图如图2所示。冰晶冰水含量估计的计算步骤如下:

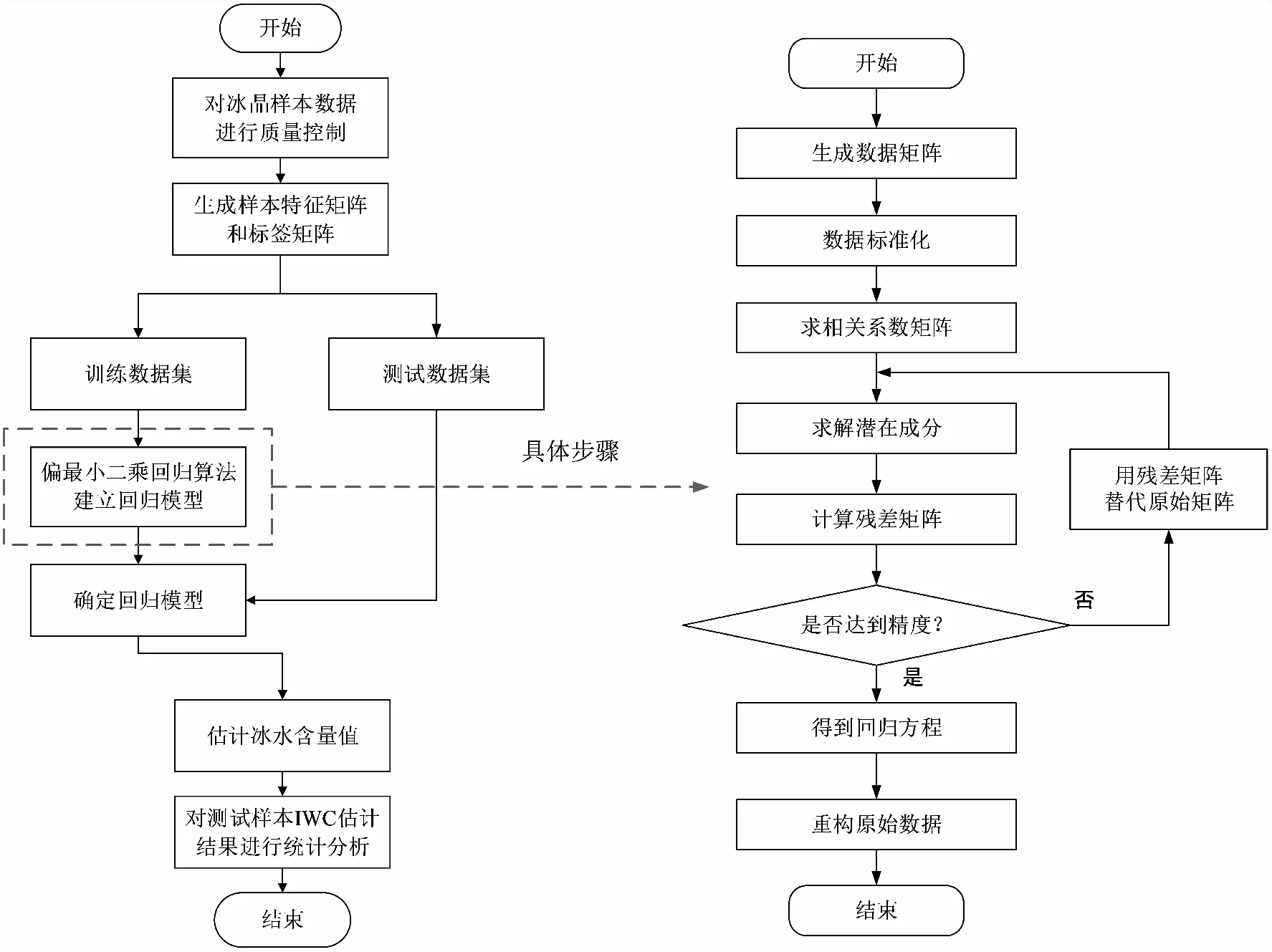
图2 算法流程

1)步骤一:对冰晶样本数据进行质量控制;

2)步骤二:生成样本特征矩阵和标签矩阵;

3)步骤三:将所有冰晶样本数据划分为训练数据集和测试数据集;

4)步骤四:将训练数据集的特征矩阵和标签矩阵带入回归模型,利用偏最小二乘回归算法建立回归模型;

5)步骤五:将标准化的回归变量还原成原始变量,确定回归模型的最终形式;

6)步骤六:将测试数据集的特征矩阵输入确定好的回归模型中,计算测试样本的冰水含量值;

7)步骤七:对冰晶样本冰水含量估计结果与样本真实冰水含量进行对比统计分析,判断估计结果的准确性,验证算法性能。

3 实验结果分析

本文针对墨西哥湾地区纬度北纬28.8°～30.4°,经度西经85.9°～87.7°区域内的含有高空冰晶天气的气象仿真数据进行实验分析。该区域位于沿海地区属于热带气候,仿真气象场景时间选取2015年8月16日,当天该地区有典型深对流云产生。高空冰晶主要出现在对流云顶层的冰云中,其高度主要分布在6～15km范围内。为了验证本文方法的有效性,分别对不同高度层的气象场景数据进行冰晶冰水含量估计实验。如图3所示为针对该场景不同高度层的气象数据分别采用本文方法与Atlas、Aydin和Mace等人[10]分别给出的经验公式法进行冰晶冰水含量估计的结果对比图。

图3 不同高度层数据冰晶冰水含量估计结果对比图

由图3所示对比结果可以看出,传统经验公式法仅使用雷达反射率因子对冰水含量进行估计且受经验取值限制,泛用性差,冰晶冰水含量估计结果均与真实值之间存在较大的偏差。而采用本文所述多重多元回回归算法进行冰晶冰水含量估计,冰晶冰水含量估计值与真实值基本一致,误差较小,说明采用多重多元回归算法实现的冰晶冰水含量估计效果优于经验公式仅利用雷达反射率因子进行冰晶冰水含量估计的方法。

分别对不同高度层数据进行实验,对冰水含量估计结果统计分析如下,冰晶冰水含量估计结果与真值之间相关系数如表1所示。

表1 冰晶冰水含量估值与真值之间的相关系数

相关性系数越接近1说明算法估计的越准确,由表1可见,不同高度层的测试数据冰水含量估值与真值之间的相关系数都大于0.8,平均值达到了0.8884,具有很强的相关性,说明误差较小估计结果较为准确。

图4为本文方法得到的高空冰晶冰水含量与真实值的相关性散点图。阴影数据点横坐标所对应的是采用本文方法得的冰水含量值,纵坐标是冰水含量真值,当冰晶冰水含量的估计值完全等于其真实值时,每个样本点的横纵坐标数值均相等,即分布在对角线上,则越接近对角线表示冰水含量估计值的准确程度越高。由图4可见,冰晶样本点大部分都分布在对角线附近,说明算法估计结果都较为准确。

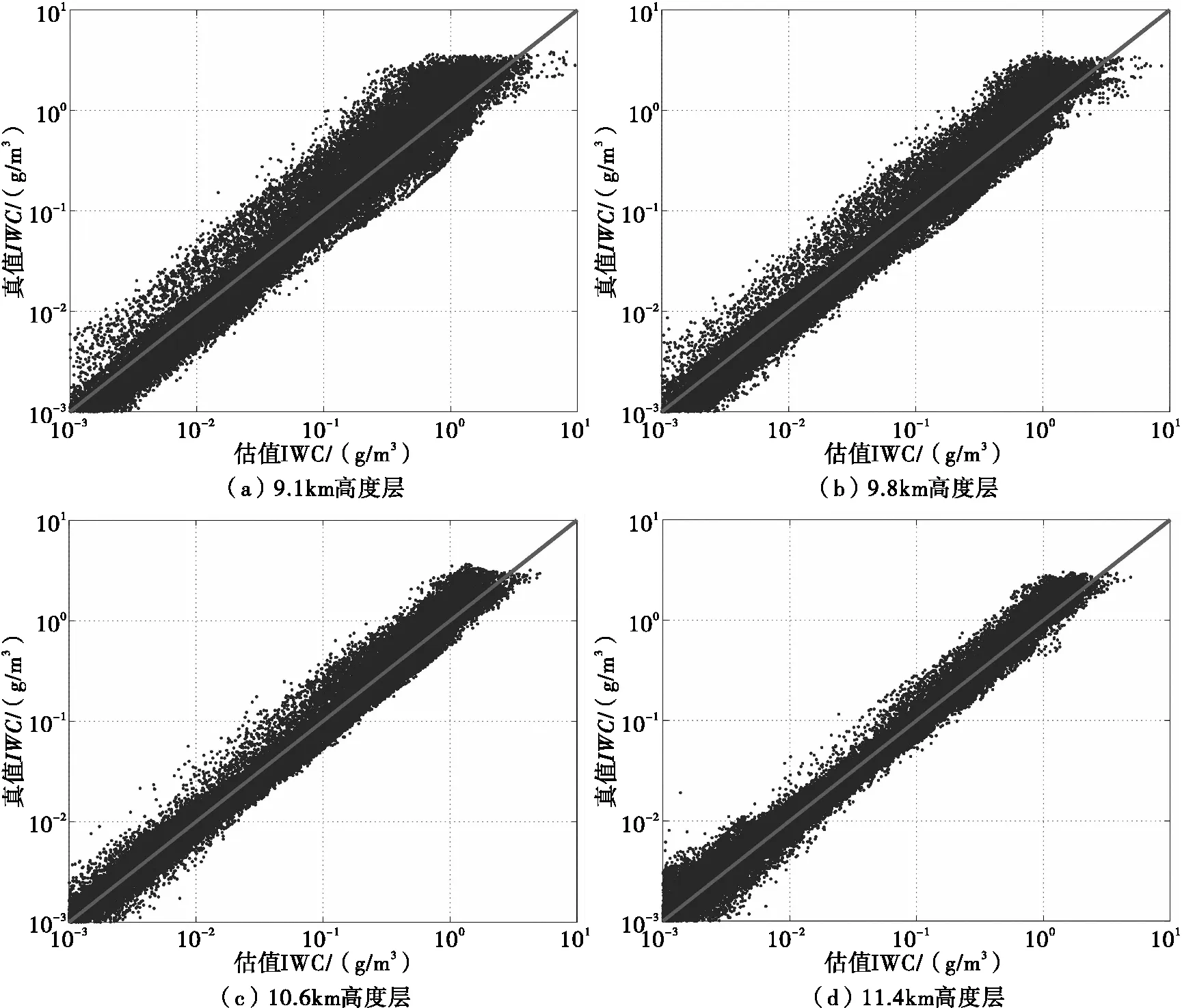
图4 不同高度层数据冰晶冰水含量估计结果相关性散点图

对于不同高度层测试数据的冰水含量回归估计结果进行误差统计,统计误差小于0.05g/m3的样本数占总样本数的百分比,结果如表2所示。

表2 误差小于0.05g/m3的样本数占比

由表2可见,对不同高度层的数据进行实验,计算得到误差小于0.05g/m3的样本数占总样本数的比例平均值为75.67%,说明大部分样本的冰晶冰水含量估计结果较为准确。以9.8 km高度层数据为例对冰水含量估计结果进行统计分析,表3为冰晶样本原始数据和回归算法估计的结果中不同冰水含量的冰晶样本占总体数量的比重,结合表3结果分析可知:回归算法估计结果与真实情况基本一致,大部分样本都小于1g/m3,大于1.5g/m3的样本估计结果相差较大是因为大于1.5g/m3的样本数量较少。

表3 不同浓度范围的冰晶样本占数据总体的比重

4 结束语

本文提出了一种基于多重多元回归的高空冰晶冰水含量估计方法,分析验证了将回归算法引入高空冰晶冰水含量估计的可行性。将冰晶的雷达反射率因子、高度和温度等特征作为代表冰晶样本的特征向量,将冰晶目标的冰水含量估计问题转化为多重多元回归预测问题,利用训练好的回归模型最终实现高空冰晶的冰水含量估计。针对典型深对流区域仿真数据进行实验分析表明,该方法可有效地估计高空冰晶的冰水含量,相比于仅利用雷达反射率因子的经验公式方法,结果更为准确。

附录：

(A-1)

将公式(A-1)第一个式子转置,第二个式子保持不变可得

(A-2)

(A-3)

即可得到λ1=θ1。

则公式(6)可转换为

(A-4)