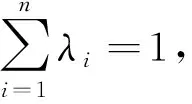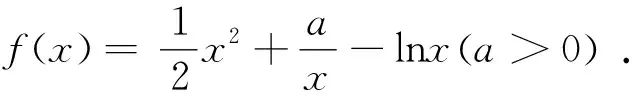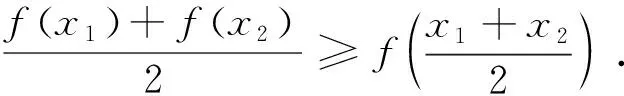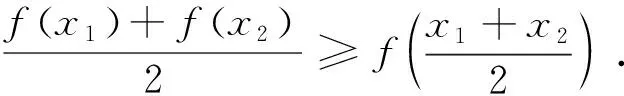2022年高考北京卷导数题的溯源、求解与推广*
2023-07-15山东省宁阳县复圣中学271400张志刚
山东省宁阳县复圣中学 (271400) 张志刚
1 题目呈现
题目(2022年高考北京卷第20题)已知函数f(x)=exln(x+1).
(1)求曲线y=f(x)在点(0,f(0))处切线方程;
(2)设g(x)=f′(x),讨论函数g(x)在[0,+∞)上的单调性;
(3)证明:对任意的s,t∈(0,+∞),有f(s+t)>f(s)+f(t).
本题主要考查导数的几何意义、利用导数研究函数的单调性及不等式的证明.考查逻辑推理、数学运算、直观想象等核心素养,考查函数与方程、数形结合、转化与化归的数学思想,体现了高考基础性、综合性、应用性、创新性的考察要求.试题设计简捷清新,内蕴丰富,具有较高的探究价值.
2 题目解答
前两问是利用导数探讨函数图象的切线、单调性等基础问题,为第(3)问证明不等式奠定了基础.
下面重点探讨第(3)问.
思路一 构造函数证明

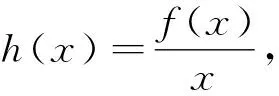
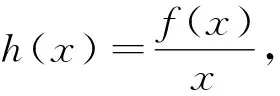
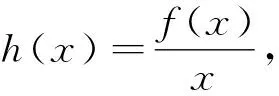
解法3:不妨设s≥t>0,设h(x)=f(x+t)-f(x)(x>0),则h′(x)=f′(x+t)-f′(x)=g(x+t)-g(x).由(2)知g(x)在(0,+∞)上单调递增,所以g(x+t)>g(x),所以h′(x)=g(x+t)-g(x)>0,故h(x)在(0,+∞)上单调递增,所以h(s)>h(0),即f(s+t)-f(s)>f(t)-f(0),又f(0)=0,所以f(s+t)>f(s)+f(t),命题得证.
点评:本解法充分利用第(2)问g(x)的单调性结论,构造差函数h(x)=f(x+t)-f(x),借助h(x)在(0,+∞)上单调递增证明结论.当然也可将f(x)的解析式代入h(x),但运算量有显著增加.
思路二 综合不等式放缩与构造函数证明
由于f(x)=exln(x+1)的解析式中含有指数函数和对数函数等初等超越函数,可考虑应用切线不等式ex>x+1(x>0)等工具合理放缩,将超越函数转化为线性函数,以降低思维难度.
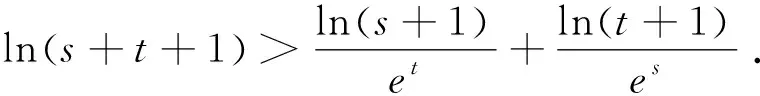

思路三 运用主副元思想证明
本问结论中含有两个地位对等的变元s,t,而证明双元不等式的核心思想就是减元(消元),主副元法就是一种常见的消元方法,其基本原理是:在双元函数不等式中,将其中一个变量作为主元,另外一个变量作为副元(参数),从而构造一元函数来证明,达到减元的目的.[1]
解法5:不妨设s≥t>0,以s为主元,设F(s)=f(s+t)-f(s)-f(t)(s>0),则F′(s)=f′(s+t)-f′(s)=g(s+t)-g(s),由(2)知g(x)在(0,+∞)上单调递增,所以g(s+t)>g(s),从而F′(s)=f′(s+t)-f′(s)>0,所以F(s)在(0,+∞)上单调递增,所以F(s)>F(0)=f(t)-f(0)-f(t)=0,即F(s)>0,即有f(s+t)>f(s)+f(t).命题得证.
点评:证得“F(s)在(0,+∞)上单调递增”后,可得F(s)≥F(t)=f(2t)-2f(t),又F′(t)=2(f′(2t)-f′(t))=2(g(2t)-g(t))>0,故F(t)在(0,+∞)上单调递增,F(t)>F(0)=0,F(s)>0,即有f(s+t)>f(s)+f(t),同样可证.
3 命制背景剖析
本题命制的背景是函数的凸性.
凸函数的定义:设函数f(x)是定义在区间I上的函数,若∀x1,x2∈I,λ∈(0,1),总有f(λx1+(1-λ)x2)≤λf(x1)+(1-λ)f(x2),则称f(x)是I上的凸函数.(将定义中的“≤”改为“≥”,则称f(x)是I上的凹函数)

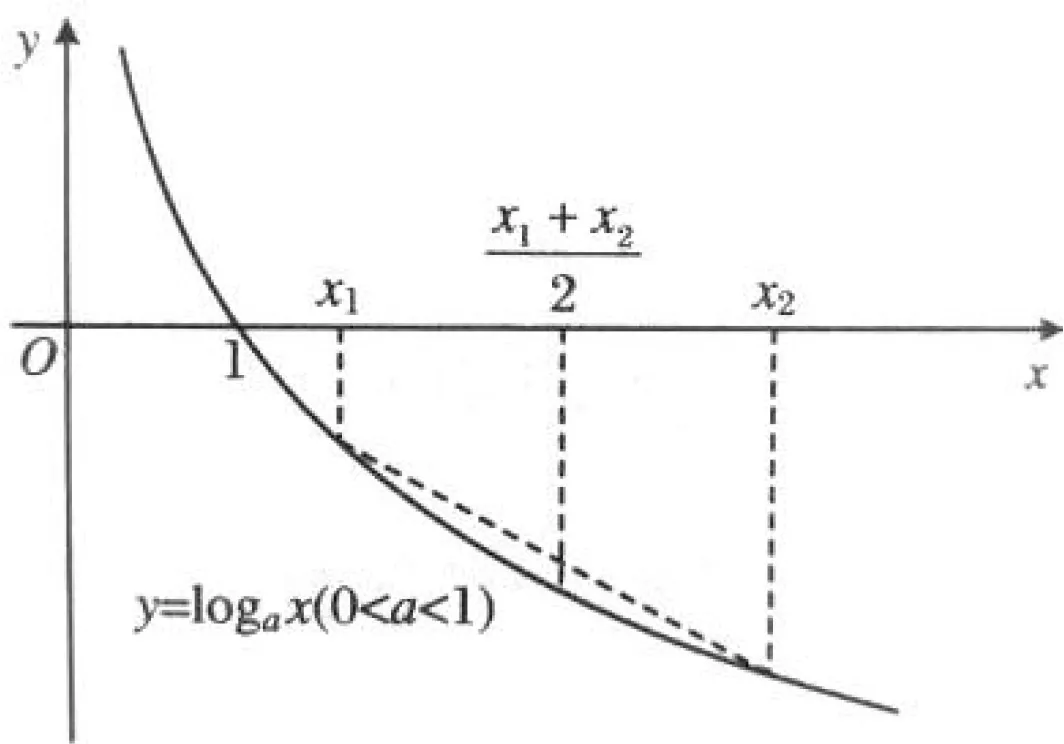
图1
凸函数的几何解释:用割线刻画:在函数的图象上自左向右任取三个不同点A(x1,y1),B(x2,y2),C(x3,y3)(x1 图2 定理1 设f(x)是区间I上的可导函数,则f(x)在I上为凸函数的充要条件是f′(x)在I上单调递增. 定理2 设f(x)是区间I上的二阶可导函数,则f(x)在I上为凸函数的充要条件是f″(x)≥0(x∈I). 图3 图4 将(*)式中的变量到推广到n个的情形,即得定理3. 以凸函数或琴生不等式为背景的试题大量分布于高考、竞赛、强基计划测试等各类试题中,试题综合性强,具有较好的区分度.下面再举两例说明. (1)当a=6时,求函数f(x)的单调区间; (1)若函数f(x)在[1,+∞)上单调递增,求实数a的取值范围; (2)设正实数λ1,λ2满足λ1+λ2=1,当a>0时,求证:对任意的两个正实数x1,x2,总有f(λ1x1+λ2x2)≤λ1f(x1)+λ2f(x2)成立. (3)当a=2时,若正实数x1,x2,x3满足x1+x2+x3=3,求f(x1) +f(x2) +f(x3) = 3的最小值. (3)先证:对任意正实数x1,x2,x3和正实数λ1,λ2,λ3满足λ1+λ2+λ3=1,总有f(λ1x1+λ2x2+λ3x3)≤λ1f(x1)+λ2f(x2)+λ3f(x3)①. 点评:本题第(2)问的高等数学背景也是凸函数的定义,由f″(x)>0知f(x)是凸函数,所以对任意的两个正实数x1,x2,总有f(λ1x1+λ2x2)≤λ1f(x1)+λ2f(x2)成立.根据变量x1,x2的对称性,将其中一个(如x1)选为主元构造函数进行论证.第(3)问的背景是琴生不等式,第(2)问的结论为第(3)问作了铺垫,从二维到三维,变量增多了,但不变的是性质.[2]
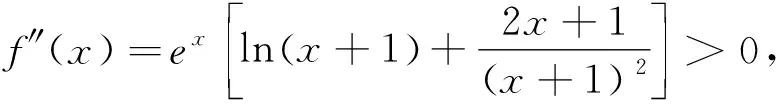



4 结论推广