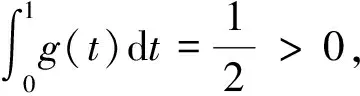一类非线性二阶半正周期问题正解的存在性①
2023-07-15王晶璇
王晶璇
西北师范大学 数学与统计学院,兰州 730070
正解的存在性, 其中λ为正参数,均为连续函数, ω是[0, 1]上的连续函数且|ω(t)|≤k, f:[0, ∞)[0, ∞)为连续函数且满足 运用锥上不动点定理证明了: 存在常数λ*>0, 使得对于λ∈(0, λ*), 该问题至少有一个正解.
近年来, 二阶微分方程边值问题受到许多学者的关注[1-14].特别地, 自然界中存在着大量的周期现象且这些周期现象可以通过二阶微分方程周期边值问题[3-14]来刻画.比如文献[5]研究了二阶周期边值问题
(1)
正解的存在性, 其中a>0,λ是一个正参数, 并且满足条件:


文献[5]运用锥上不动点定理, 得到了:

值得注意的是, 文献[5]研究了非线性项f非负的情况下问题(1)正解的存在性, 且a为常数.受上述文献启发, 本文考虑比问题(1)更广泛的问题.具体地, 本文研究二阶周期半正问题
(2)
正解的存在性, 其中λ是一个正参数.我们得到如下结论:
定理1假定以下条件成立:



(H4)ω是[0, 1]上的连续函数, 且|ω(t)|≤k.
则存在常数λ*>0, 使得当0<λ<λ*时, 问题(2)至少存在一个正解uλ.
注1当ω=0时, 定理1就退化为引理1的结果.然而, 我们所要研究的是允许|ω|≠0的情形, 允许非线性项取负值的情况下正解的存在性结果.因此, 我们所得的结果是对引理1的推广.
1 预备知识

Lu=-u″+a(t)uu∈D(L)
其中
D(L)={u∈C2[0, 1]:u(0)=u(1),u′(0)=u′(1)}
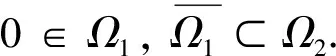
是全连续算子, 且满足
(i)‖Au‖≤‖u‖,u∈K∩∂Ω1且‖Au‖≥‖u‖,u∈K∩∂Ω2;
或
(ii)‖Au‖≥‖u‖,u∈K∩∂Ω1且‖Au‖≤‖u‖,u∈K∩∂Ω2.
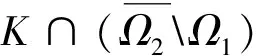
定义u(x),v(x)是齐次方程
-y″+a(t)y=0 0≤t≤1
满足初值条件
y(0)=1y′(0)=0
的解.且定义
D=u(1)+v′(1)-2
根据文献[6]中的定理2.5, 下述引理成立:
引理3假设条件(H3)成立且h为非负连续函数, 则线性问题
存在唯一解

其中
且G(t,s)>0, ∀t,s∈[0, 1].
令
则m>0,M>0.
由于g(t)是[0, 1]上的连续函数, 则g(t)在[0, 1]上有上界, 记为T, 即0 引理4令w是 证由引理3知 则 引理5令u∈C1[0, 1]∩C2(0, 1), 满足 证令v0(t)是微分方程 的唯一解, 则 即-v0(t)≤MkT, 则v0(t)≥-MkT. 令y(t)=u(t)-v0(t), 则 定理1的证明问题(2)的等价积分形式为 (3) 定义E中的集合 其中 则K为E中的一个正锥. 若u∈K, 结合引理5和(3)式可知 令a>1, 有 f(z)+ω(t)>0z≥a,t∈(0, 1) (4) 即 因此, 如果u∈K且‖u‖=H1, 则由(3),(4)式得 令 Ω1={u∈E: ‖u‖ 则有 ‖Au‖≤‖u‖u∈K∩∂Ω1 (5) (6) 令 Ω2={u∈E: ‖u‖ 则有u∈K且‖u‖=H2, 则 (7) 因此, 由(6)式和(7)式得 因此 ‖Au‖≥‖u‖u∈K∩∂Ω2 (8) 例1考虑问题 (9) 解的存在性, 其中λ>0. 解这里取 a(t)=t+1g(t)=tf(u)=u2ω(t)=sin 2πt 对于问题(9)而言, 显然f是连续的非负函数, 且有 根据定理1可得, 存在常数λ*>0, 使得当0<λ<λ*时, 问题(9)至少存在一个正解uλ.
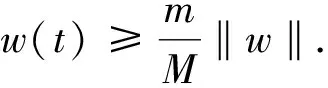
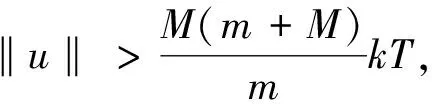

2 主要结果的证明


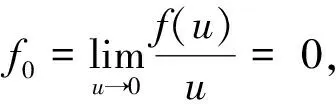



3 应用