基于VB-AUKF的GNSS/SINS组合导航信息融合算法

2023-07-14孙玉梅潘新龙王美春

弹箭与制导学报 2023年3期

孙玉梅，潘新龙，王美春

(1 潍坊科技学院计算机学院，山东潍坊 262700；2 海军航空大学，山东烟台 264001)

0 引言

经典线性卡尔曼滤波采用线性高斯状态空间模型,是GNSS/SINS组合导航系统经常采用的信息融合方式[1]。当系统的非线性比较严重时,扩展卡尔曼滤波(EKF)的估计不准确,而无迹卡尔曼滤波(UKF)可以降低EKF线性化带来的误差,可以将组合导航系统扩展到非线性滤波模型[2]。然而,UKF方法的一个严重缺陷是假设准确的系统模型及已知的先验噪声统计特性,而这个假设在实际环境下不成立[3]。

自适应滤波是解决上述问题的有效方法,在估计系统状态参数的同时也可以估计噪声统计特性。而贝叶斯方法是目前最普遍应用的方法,包括协方差匹配法、极大似然法均为贝叶斯方法的近似方法[4]。而变分贝叶斯方法具有较低的计算成本,可以近似求解贝叶斯方法中高度耦合的高维隐变量的后验推理,近年来在诸多领域得到应用,如情报监测[5]、目标跟踪[6]、雷达系统[7]等。

近年来,将变分贝叶斯方法与线性卡尔曼滤波技术相结合而形成的VB-KF算法在组合导航系统也得到较深入的研究[8]。如:文献[8-9]将VB-KF技术应用于GNSS/SINS组合导航系统;文献[10]、文献[11]分别将VB-KF技术应用于同步与异步多传感器组合导航系统;针对VB-KF技术对噪声跟踪性能差的问题,文献[12-13]提出了基于T分布的变分高斯滤波算法,但是该方法将量测噪声建模为T分布、导致不能单独调节噪声方差内独立变化的噪声。同时,上述文献的共同特点是采用线性卡尔曼滤波方法,无法有效解决模型误差导致的滤波精度下降问题。

为此,文中将变分贝叶斯方法与UKF算法相结合,在对GNSS/SINS组合导航系统进行变分贝叶斯自适应UKF非线性滤波建模的基础上,提出了量测噪声方差自适应估计的迭代模型。

1 变分贝叶斯估计模型

对于状态方程非线性而量测方程线性的离散时间非线性系统[10]:

(1)

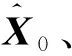
对于式(1)模型,如果Rk是时变的或未知的,则贝叶斯最优滤波的目标是计算系统状态和量测噪声方差矩阵的联合后验分布p(Xk,Rk|Z1∶k),此时该滤波过程包含以下步骤[14-15]:

1)初始化:计算系统状态和量测噪声方差矩阵的先验分布p(X0,R0)。

2)预测:系统状态向量Xk与测量噪声方差矩阵Rk的联合预测分布由Chapman-Kolmogorov方程给出[16]:

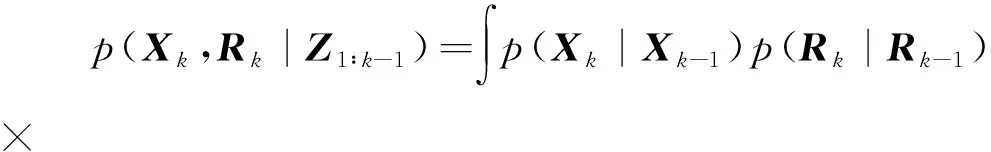
(2)

3)更新:给定下一个测量值Zk,通过贝叶斯规则将上述预测分布更新为后验分布:

p(Xk,Rk|Z1∶k)∝p(Zk|Xk,Rk)p(Xk,Rk|Z1∶k-1)

(3)

式(2)、式(3)所涉及的积分通常是无法解析处理的,可利用后验变分近似表示为[17]:

p(Xk,Rk|Z1∶k)=QX(Xk)QR(Rk)

(4)

其中:

(5)

式(5)中两个方程相互耦合,为此,对两个方程的期望进行评估及参数匹配,得到密度:

(6)

则式(2)、式(3)变为[16]:

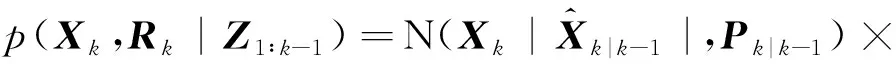
(7)

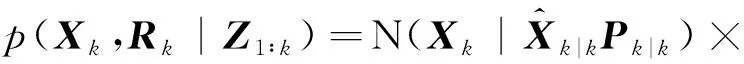
(8)

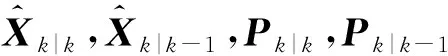
(9)

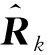
(10)

为了使观测噪声的变化规律具有自适应调整特性,引入因子ρi∈(0,1]。对于i=1,2,…,d,则有[16]:

(11)

2 基于变分贝叶斯的组合导航UKF算法

2.1 变分贝叶斯UKF算法

根据系统模型,将标准UKF算法与变分贝叶斯估计模型相结合,得到组合导航系统的基于变分贝叶斯的自适应UKF算法(VB-AUKF):

对于式(1)所示的非线性系统,将系统状态和系统噪声进行合并,得到增广状态向量:

(12)

式中:χa,χX和χW分为Xa,Xk和Wk的采样点向量,假设其维数分别为N,Lx,Lw,则N=Lx+Lw。

步骤1:初始化

(13)

步骤2:样点计算

(14)

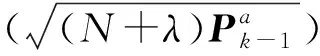
(15)

其中:λ=α2(N+κ)-N;α,β和κ为比例因子。

步骤3:时间更新

(16)

(17)

(18)

其中:ρ=[ρ1ρ2…ρd]T;α=[α1α2…αd]T;β=[β1β2…βd]T。

步骤4:量测更新

(19)

(20)

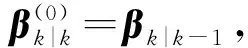
(21)

(22)

(23)

(24)

式(21)～式(24)中,1≤j≤J。

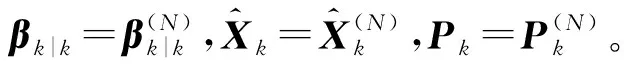
2.2 GNSS/SINS组合导航系统模型

GNSS/SINS组合导航系统非线性滤波的状态方程采用SINS的力学方程,组合导航系统的导航参数直接选取为被估计的状态。选取“东北天”地理坐标系为导航坐标系,则连续时间系统的状态方程为:

(25)

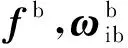
选取GNSS接收机输出的三维速度和三维位置直接作为观测向量,则量测方程可以表示为:

(26)

对式(25)、式(26)进行离散化处理可以得到离散化的状态方程及量测方程。

3 仿真结果与分析

在Matlab环境下进行仿真,首先评估参数ρ,α,β的取值对量测噪声未知均方差估计的影响,然后评估GNSS/SINS组合导航系统VB-AUKF算法的滤波性能。

3.1 仿真条件

以飞行器作为仿真对象,其飞行过程包含各种机动运动。初始位置为(118°E,29°E,50 m),仿真时间为3 600 s;滤波周期为1 s。初始参数设置如表1所示。

表1 导航传感器误差参数设置Table 1 Navigation sensor error parameter setting

根据表1所示的GNSS误差设置,则正常情况下GNSS量测噪声的均方差为:

rroot=sqrtm(R)=diag([0.2 0.2 0.2 8 8 8])

(27)

其中函数sqrtm(·)的功能是对矩阵中每个元素取开平方。

为了验证系统算法性能,在飞行器飞行期间设定GNSS量测噪声均方差变化为:

(28)

3.2 仿真校验

以下的仿真实验均是以相同的导航仿真原始数据为基础,对式(21)～式(24)的迭代步数取j=2。

3.2.1 参数ρ对未知方差估计的影响

为了评估ρ对量测噪声未知方差估计精度的影响,首先使得α,β的取值不变并设定为:

(29)

对参数ρ的取值,定义方案A:

方案A1:ρ=[0.85 0.85 0.85 0.85 0.85 0.85]

方案A2:ρ=[0.90 0.90 0.90 0.90 0.90 0.90]

方案A3:ρ=[0.95 0.95 0.95 0.95 0.95 0.95]

方案A4:ρ=[1 1 1 1 1 1]

方案A5:ρ=[0.99 0.99 0.99 0.99 0.99 0.99]

基于上述5种方案,图1～图2为利用文中算法估计到的位置误差及速度误差均方差曲线。

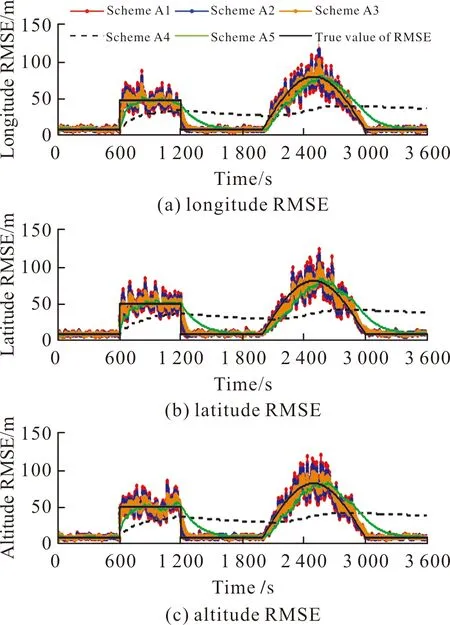
图1 GNSS位置噪声均方差估计曲线Fig.1 GNSS position noise RMSE estimation curve

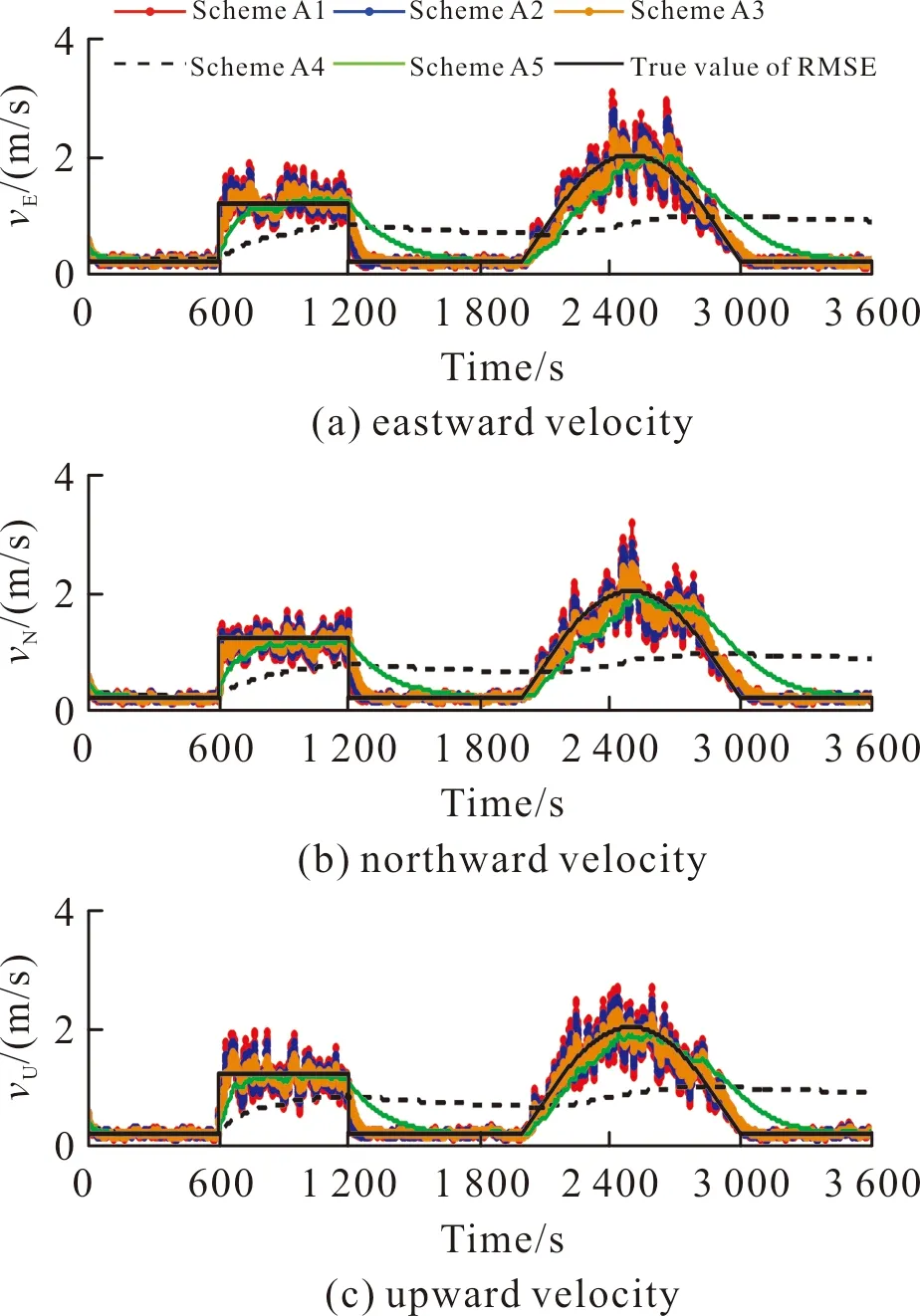
图2 GNSS速度噪声均方差估计曲线Fig.2 GNSS velocity noise RMS estimation curve

由图1～图2可见,当ρ中的元素ρi=1(i=1,2,…,d;d=6)时,变分贝叶斯算法适合于估计平稳噪声的均方差(方案A4);ρi<1并接近于1时,文中算法估计的量测噪声均方差在实际均方差变化结束时存在较严重的“拖尾”现象(方案A5);当ρi<0.9时,估计到的均方差能较精确地反映实际均方差的变化规律,但是估计曲线波动幅度随着ρi的减小而增大(方案A1、方案A2)。

实验证明,当0.95≤ρi≤0.97时,文中算法估计到的均方差效果较好,不仅能反映实际均方差的变化规律,而且估计曲线波动幅度较小(方案A3)。

3.2.2 参数α对未知方差估计的影响

为了评估α对量测噪声未知方差估计精度的影响,首先使得ρ,β的取值不变并设定为:

(30)

方案B1:α=[1 1 1 1 1 1]

方案B2:α=0.2×[1 1 1 1 1 1]

方案B3:α=5×[1 1 1 1 1 1]

基于上述3种方案,图3～图4为利用文中算法估计的位置误差及速度误差均方差曲线。

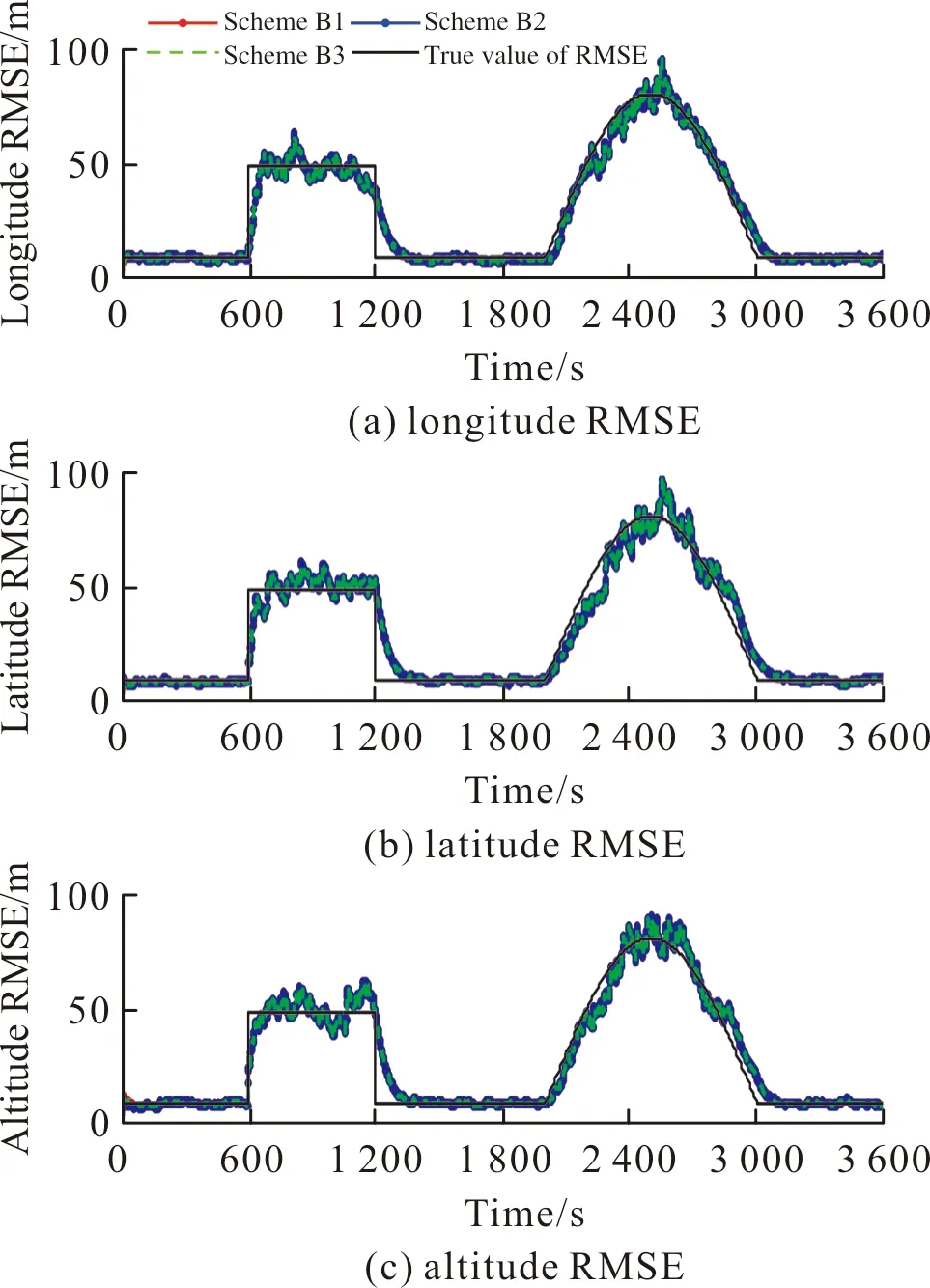
图3 GNSS位置噪声均方差估计曲线Fig.3 GNSS position noise RMSE estimation curve

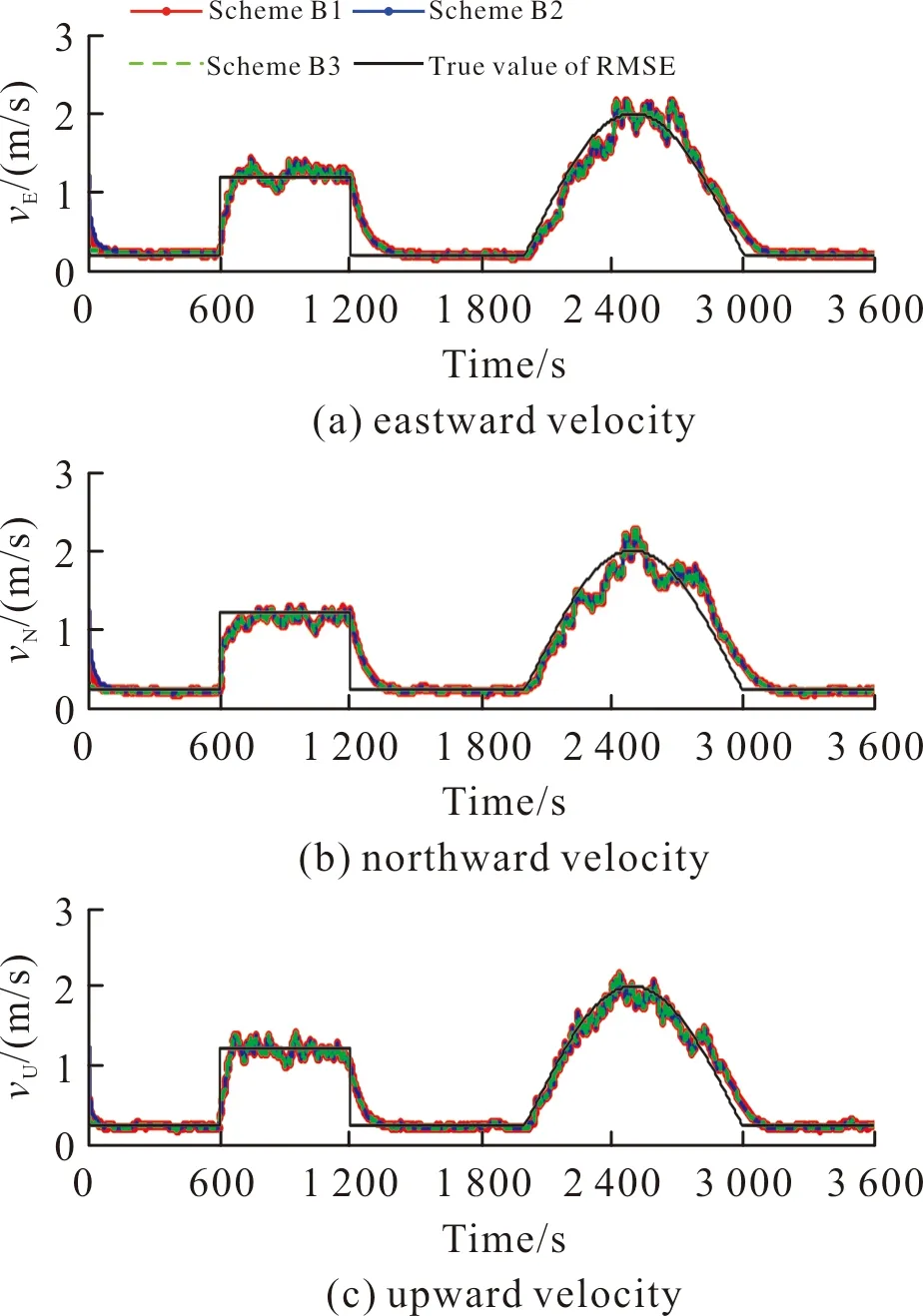
图4 GNSS速度噪声均方差估计曲线Fig.4 GNSS velocity noise RMSE estimation curve

由图3～图4可以看出,当ρ,β不变时,α的选择仅仅改变均方差的初始估计值,经过短时间后α的选择对均方差的估计值无影响。

3.2.3 参数β对未知方差估计的影响

为了评估β对量测噪声未知方差估计精度的影响,首先使得α,ρ的取值不变并设定为:

(31)

方案C1:β=[0.3 0.3 0.3 6 6 6]

方案C2:β=3×[0.3 0.3 0.3 6 6 6]

方案C3:β=[0.02 0.02 0.02 32 32 32]

基于上述3种方案,图5～图6为利用文中算法估计的位置误差及速度误差均方差曲线。

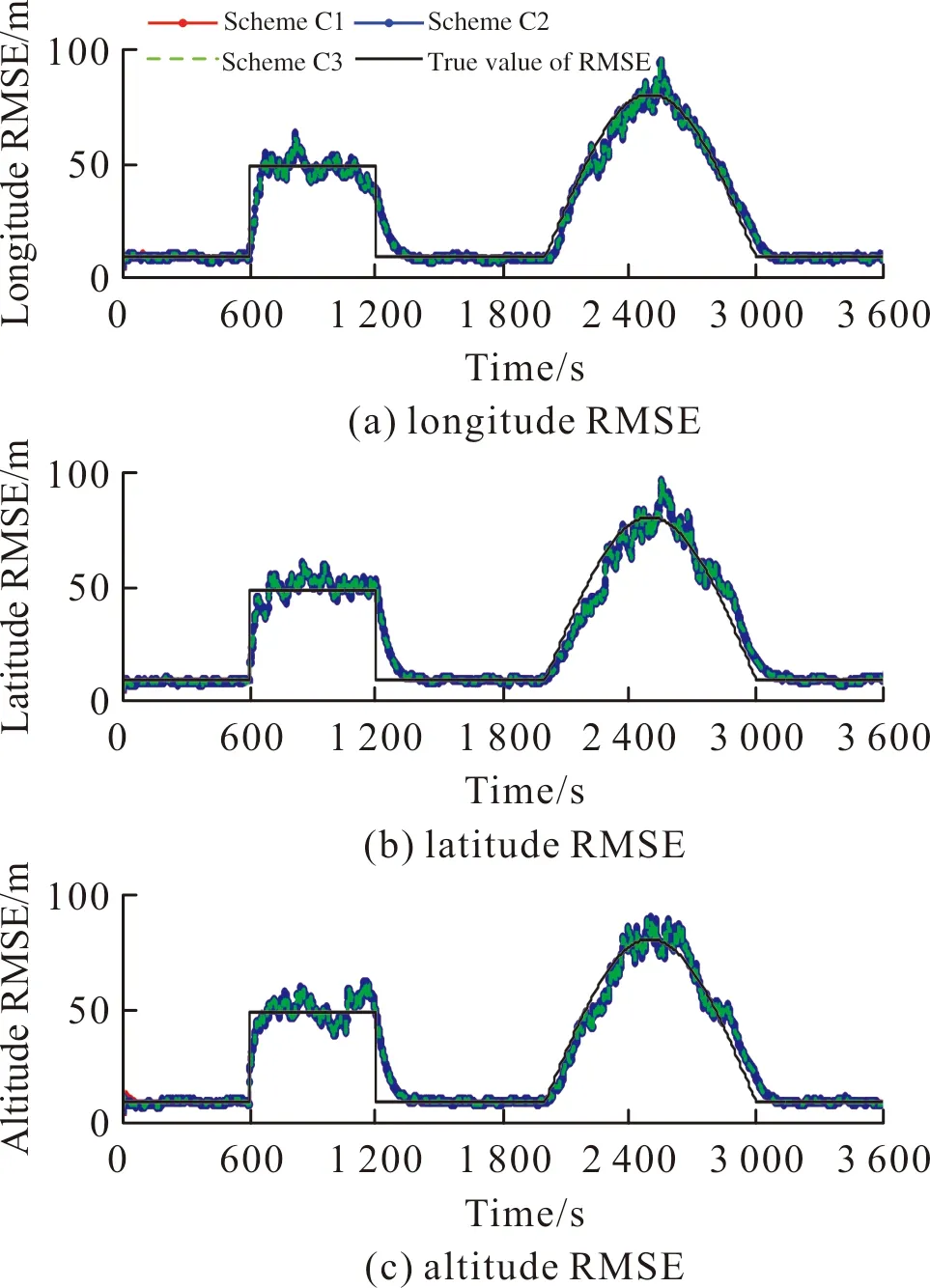
图5 GNSS位置噪声均方差估计曲线Fig.5 GNSS position noise RMSE estimation curve

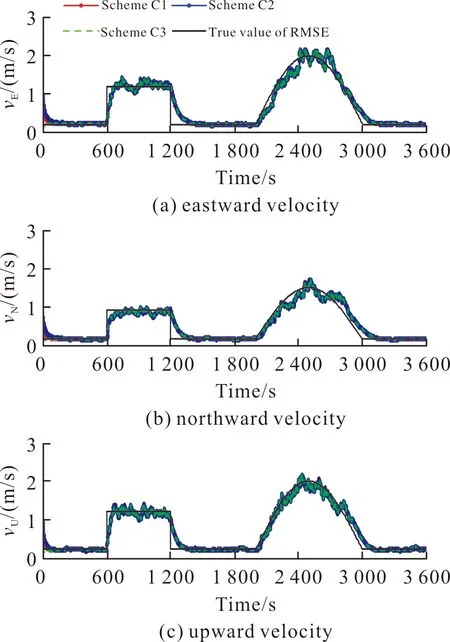
图6 GNSS速度噪声均方差估计曲线Fig.6 GNSS velocity noise RMSE estimation curve

由图5～图6可以看出,当α,ρ不变时,β的选择也仅仅改变均方差的初始估计值,经过短时间后β的选择对均方差的估计值无影响。

同时,综合对比图1～图6,可以看出,当ρ的值不变时,α和β值的选择仅仅改变了均方差的初始估计值,经过短时间后α和β值的选择对均方差的估计值无影响;对均方差估计结果影响的决定参数是ρ。所以,只要ρ的取值处于合理区域,文中算法估计到的量测噪声均方差具有较好的稳定性。

3.2.4 基于VB-AUKF的组合导航实验

图7～图9给出了基于标准UKF算法及文中算法方案15的组合导航系统位置误差、速度误差及姿态误差曲线对比图。由图7～图9可以看出,由于标准UKF算法对量测噪声均方差无自适应调节能力,所以当量测噪声均方差发生变化时标准UKF算法得到的导航参数误差较大;而文中算法由于对量测噪声均方差的自适应调节能力较强,故可以保证系统的滤波精度。

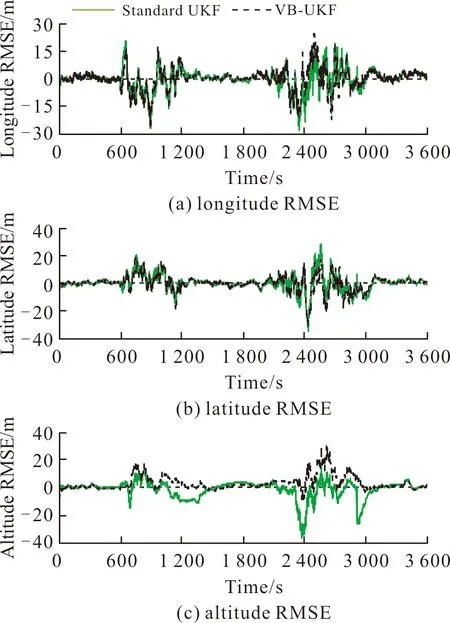
图7 位置误差曲线对比图Fig.7 Position error curve comparison

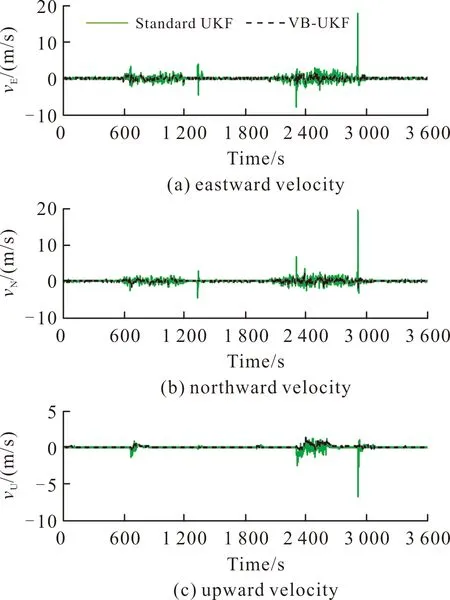
图8 速度误差曲线对比图Fig.8 Velocity error curve comparison

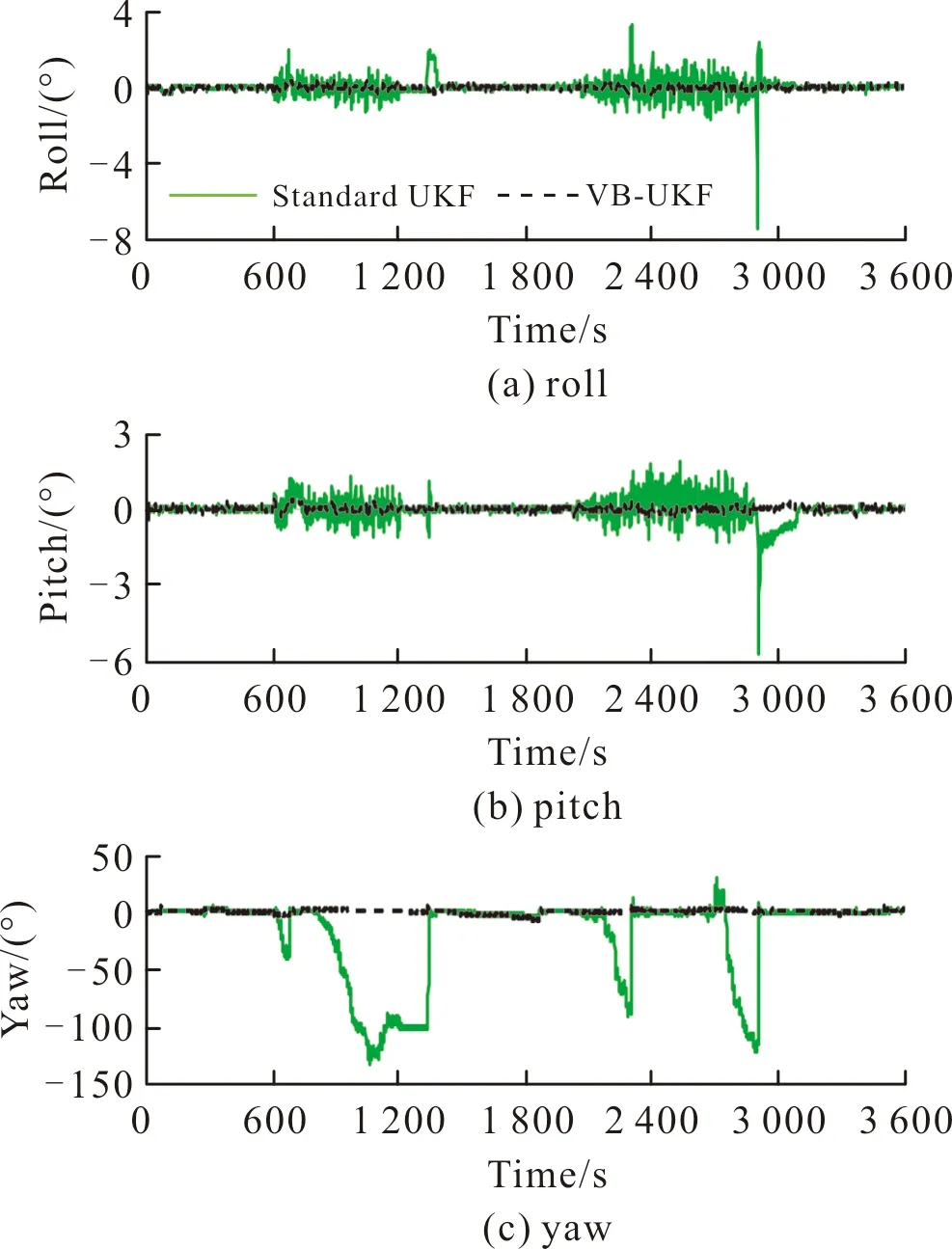
图9 姿态误差曲线对比图Fig.9 Attitude error curve comparison

当前述的迭代步数j≥3时,量测噪声均方差的估计精度变化可忽略不计,且也不会对组合导航系统的滤波精度形成影响。

为了定量分析图7～图9所示的两种滤波算法的滤波精度,在整个导航时段内,表2给出了基于VB-AUKF算法及标准UKF算法的各导航参数误差均方差统计分析。

表2 基于VB-AUKF及标准UKF的导航参数误差统计分析Table 2 Statistical analysis of navigation parameter error based on VB-AUKF and Standard UKF

由表2可以看出,相对于标准UKF算法,VB-AUKF算法可提高位置精度及速度精度分别约12%及51%;提高横滚角及俯仰角精度约75%,同时可以改变航向角在量测噪声均方差变化时存在的发散现象。为此,基于VB-AUKF算法可以克服标准UKF算法不能自适应调节量测噪声均方差的缺陷,进而提高了滤波器的鲁棒性。