光纤型白光干涉仪光程差的超分辨率识别
2023-07-14侯成城郑光金尚福洲高业胜
侯成城,郑光金,尚福洲,高业胜
(中国电子科技集团公司第四十一研究所,国防科技工业光电子一级计量站,青岛 266000)
1 引言
光纤型白光干涉仪是光纤研究领域的一个重要分支[1],光纤型白光干涉仪具有许多应用,例如高精度绝对距离测量[2]、保偏器件拍长测量[3]、波导元件结构和反射特性测量[4],在这些应用中,获取信号的位置信息尤为重要,而位置信息反馈到干涉信号中表示为光程差,因此,精确测量光程差具有重要意义[5]。
为了提高白光干涉法测量光程差的准确性,已经提出了多种分析白光干涉信号的方法。Rolf 等人提出了一种通过小波滤波器分析光程差的方法[6],这种方法测量精度高,但计算量大。Young 等人提出了一种空间光路的白光干涉仪,空间光路可以提高光程差的测量精度[7],但是测量方式复杂。Patrick 等人提出了利用相干包络相位变化计算光程差零点[8]。上述的测量方法的分辨率都小于光源的相干长度,但是当干涉信号之间的光程差小于光源相干长度时,干涉信号无法区分,上述的方法也将难以适用。
阐述了一种通过识别干涉信号面积变化计算光程差的方法。首先,从理论上展示了干涉信号重叠引起面积的变化和光程差之间的关系。然后,描述了获取低分辨率干涉信号的实验步骤。最后阐述了数据处理步骤,实验结果证明该方法提升了光程差的分辨率。
2 白光干涉信号超分辨率识别理论
2.1 光程差识别基本原理
白光干涉法测量光程差原理图如图1 所示。首先,假设被测器件是一段保偏光纤,同时假设被测保偏光纤内部有两个耦合点,两个耦合点是通过外部压力挤压光纤形成的。图1(a)显示了白光光源发出光耦合到保偏光纤的慢轴上进行传输,在第一个耦合点位置l1处,慢轴传输的光会有部分能量耦合到快轴,耦合能量的百分比称之为耦合系数ρ,由于保偏器件的快慢轴中存在双折射差,两束正交方向传输的光将以不同的群速度进行传播,当慢轴中的光传输到第二个耦合点位置处l2时,快轴中传输的光将超越慢轴传输的光。在第二个耦合点处,慢轴传输的光仍会有一部分光会耦合到快轴上,由两个耦合点产生的慢轴传输的光将以一个固定的间距进行传输,这个间距就是光程差(OPD),OPD与两个耦合点的光纤距离(l2-l1)相关,后续理论部分会详细讲述OPD 与光纤距离之间的关系。在第二个耦合点处,在快轴中传输的光也会耦合一部分到慢轴中去,一般来说,二次耦合的光功率很小,所以忽略不计。

图1 白光干涉法测量光程差原理图Fig.1 The principle diagram of OPD measurement based on white light interference method
在保偏光纤输出端,快轴中传输的光通过偏振分束器转换90°偏振方向,然后快轴中传输的光通过延迟线与在慢轴中传输的光进行光程匹配,然后依次发生干涉形成两个干涉信号,图1(b)表示的是两个耦合点对应的干涉信号,此时,两个干涉信号顶点之间的距离代表这两个耦合点之间产生的光程差OPD。
两个干涉信号I(x)表达式可写为:
式中:S(ω)——随角频率ω变化的光源幅度谱;ρj(j=1,2)——两个耦合点对应的耦合系数;i——虚数;Δβ(ω)——快慢轴引入的传播常数差;lj(j=1,2)——两个耦合点的位置;c——光速。
式(1)中的Δβ(ω)经过泰勒展开之后可以表示:
式中:Δn——相速度双折射差;ΔN——群速度双折射差。
将式(2)代入式(1)中,表达式可以写为:
式中:Lc——相干长度。
从式(3)分析,当x=ΔNlj时,干涉信号的幅度值最大,因此,传统方法可以通过测量两个干涉信号最大值之间的距离来测量光程差。
2.2 光程差超分辨率识别原理
当干涉信号之间的光程差低于光源相干长度后会发生重叠,此时传统测量光程差的方法将不再适用,新方法利用信号叠加后面积变化的波动大小计算出干涉信号之间的真实光程差。白光干涉信号叠加示意图如图2 所示。图2 中用红蓝曲线显示两个干涉信号实际的轮廓,可以看出当两个干涉信号的光程差逐渐缩小时,信号将越来越难分别,图2(a)(b)显示干涉信号叠加之后虽然可以区分,但是叠加后面积却发生了变化,叠加有可能使信号面积增多,也可能使信号面积减弱,图2(c)显示叠加使干涉信号完全无法区分。
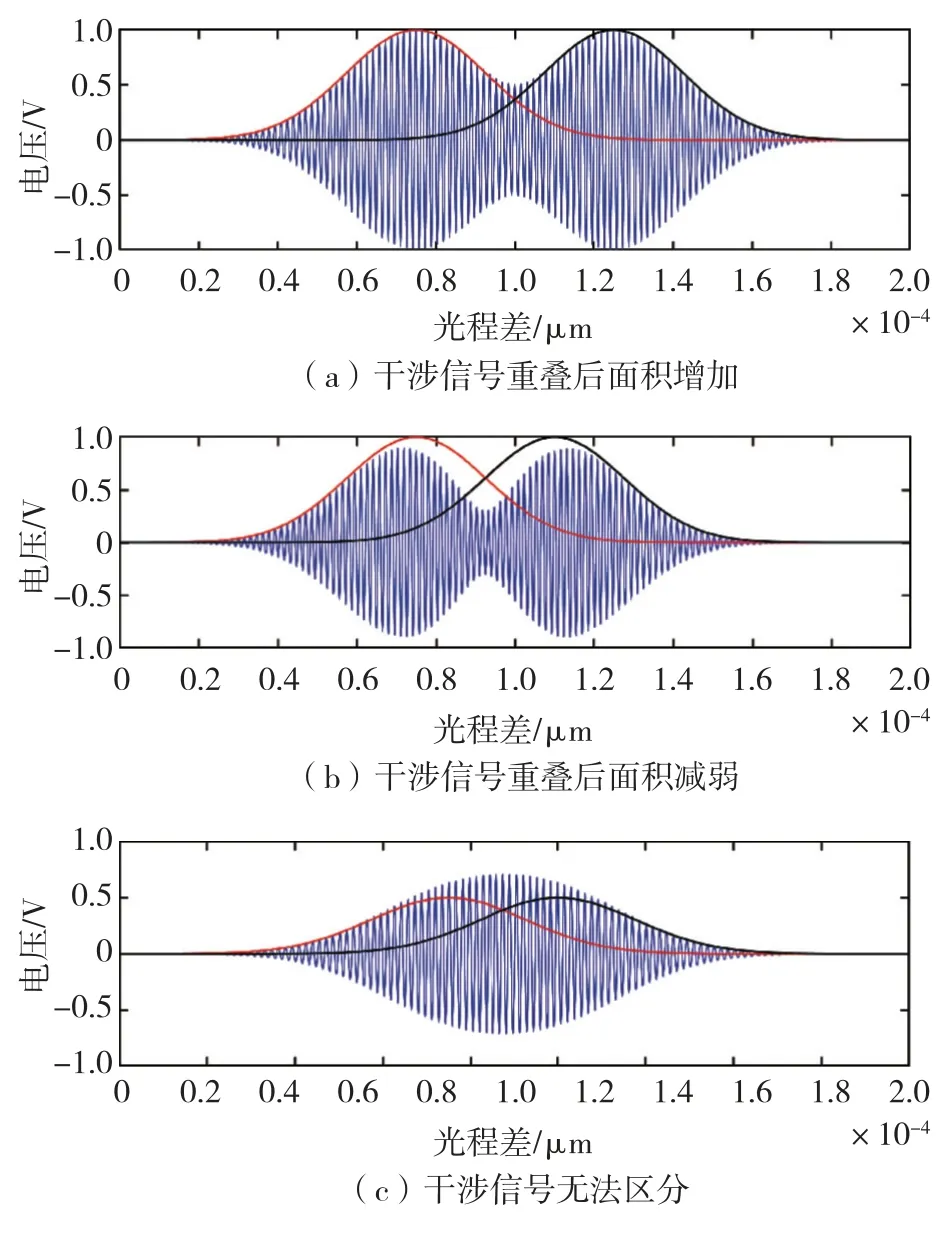
图2 白光干涉信号叠加示意图Fig.2 Schematic diagram of interference signals overlapped
与传统方法不一样,新方法通过计算信号的面积变化来测量光程差。两个干涉信号的实际面积可以写为:
式中:S1,S2——两个干涉信号的理论面积;第三项——叠加导致的面积变化。
其中,
一个干涉信号的理论面积可以表示为:
可以看出,面积与耦合系数ρj和相干长度Lc有关。由重叠区域引入的面积变化可以表示为:
如果光程差OPD大于相干长度Lc,则Ioverlap=0,S=S1+S2。如果OPD小于相干长度Lc,则Ioverlap≠0 并且S将发生变化。通过式(7)可以看出Ioverlap和cos(k0×OPD)只与光程差OPD有关,换句话说,如果测量得到叠加引入的面积变化,就可以通过式(7)计算两个干涉信号之间的光程差OPD。
从上面的讨论中可以得出如下结论:两个干涉信号叠加导致的面积变化与干涉信号之间光程差OPD有关。为了实现超分辨率识别,首先需要测量两个耦合点的耦合系数ρj(j=1,2)和光源的相干长度Lc。然后使用式(6)计算得到S1+S2。然后,利用测量得到的干涉信号计算干涉信号的实际面积S,并计算实际测量面积和理论面积的差值ΔS=S-S1-S2,差值表示重叠引起的面积变化。最后,将ΔS代入方程得到式(7)中计算得到光程差OPD。
3 光程差超分辨率识别实验结果
3.1 光路搭建和实验设计
光纤型白光干涉仪如图3 所示。它由3 个探测器、1 个采集卡、1 个马赫曾德干涉仪、一个白光光源和一台计算机组成。白光光源的中心波长为1 550 nm,相干长度为50 μm。干涉仪包含一个光纤耦合器、一个环行器、一个法拉第旋转透镜和延迟补偿。

图3 光纤型白光干涉仪原理图Fig.3 Schematic diagram of fiber optical white light interferometer
在实际做实验之前,先通过仿真确定一些实验参数,通过理论仿真发现当两个耦合点的耦合系数相差越大,由叠加引入的面积变化越小,幅度对信号形状影响仿真图如图4 所示。图4(a)仿真结果表明当两个信号的幅度接近时信号叠加引入的面积变化明显,图4(b)仿真结果表明当两个信号的幅度相差20 dB 时叠加引入的影响将可以忽略不计。因此,为了保证测量的准确性,需要保证两个耦合点的耦合系数越接近越好。

图4 幅度对信号形状影响仿真图Fig.4 Simulation results of amplitude influence on signal shape
为了制作低分辨率的干涉信号,需要设计相关实验步骤。实验中偏振器和检偏器分别采用0 °和45 °。干涉信号重叠实验过程图如图5 所示,实验将光路分为3 个部分,实验过程中最重要的部分是创建两个具有已知耦合系数的耦合点。首先,通过起偏器将设备与待测光纤进行连接,然后,将偏振光耦合到偏振器件中,同时将设备的输出端连接到消光比测试仪。然后,对待测光纤施加压力,使其成为第一个耦合点,并利用消光比测试仪测量第一个点的产生的消光比值PER1。然后,在光纤上的另一个位置处施加压力形成第二个耦合点,同时,使用测试仪测量两个点的总消光比PER2,第一个耦合点的耦合系数等于-PER1,第二个耦合点的耦合系数为-(PER2-PER1),然后,标记好这两个耦合点在光纤上的位置,之后用游标卡尺测量两个耦合点之间的光纤距离Δl,然后将设备与白光干涉仪进行连接,测量干涉信号。

图5 干涉信号重叠实验过程图Fig.5 Schematic diagram of the experimental process of interference signal overlap
白光干涉信号叠加实验结果图如图6 所示。图6(a)中有四个干涉信号,第一个和第四个干涉信号为测试系统自带的干涉信号,中间的两个信号为实验制造的两个干涉信号,两个干涉信号的顶点位置依次818.7 μm 和1 174.2 μm,两个耦合点之间产生的光程差OPD=355.5 μm,两个耦合点之间的光纤距离Δl=79.2 cm,双折射差ΔN=4.49E -4的。图6(b)和6(c)显示两个耦合点逐渐靠近并发生了重叠,此时,两个干涉信号的顶点已经无法区分,当两个干涉信号无法区分时,首先测量干涉信号的面积,然后再计算光程差。
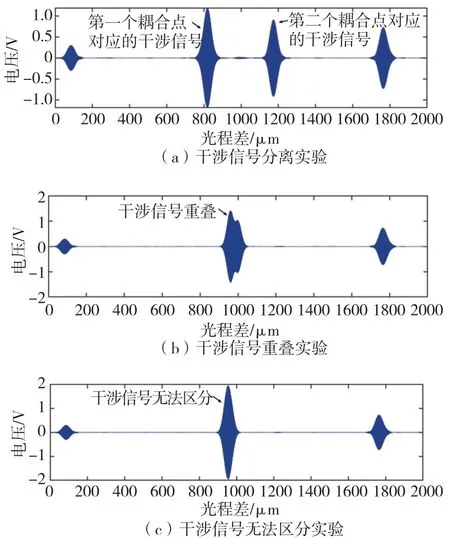
图6 白光干涉信号叠加实验结果图Fig.6 Experiment results of interference signals overlapped
3.2 超分辨率识别步骤
数据处理流程图如图7 所示。首先,记录两个耦合点产生的消光比值PER1,PER2,并采集得到干涉信号,然后利用PER1,PER2计算两个耦合点的耦合系数ρ1,ρ2,并根据式(6)计算两个干涉信号的理论面积S1和S2。然后计算干涉信号的面积S,并计算差值ΔS=S-S1-S2。最后,将ΔS代入式(7)得到OPD。

图7 数据处理流程图Fig.7 Flowchart of data processing
低于相干长度的光程差的测试结果如表1 所示。
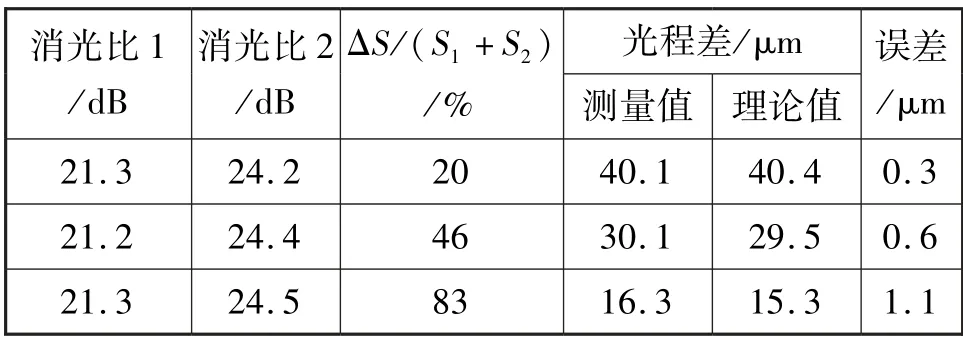
表1 低于相干长度的光程差的测试结果Tab.1 The measurement results of OPD less than coherence length
白光光源的相干长度为50 μm,光纤的双折射差ΔN=4.49E -4,光程差的理论数值可以根据两个耦合点之间的光纤距离Δl和ΔN计算得到。从表1 可以看出,低于相干长度时该方法也可以识别干涉信号之间的光程差,只是测量误差随着光程差数值越小误差越大。
4 结束语
提出了一种白光干涉信号数据处理的方法,可以实现白光干涉信号的超分辨率识别。理论证明了干涉信号叠加后面积的变化与两个信号的光程差有关。为了实现超分辨率识别,首先需要测量两个耦合点的耦合系数。然后,利用耦合系数计算得到理论面积,并利用理论面积和实际测量面积之间的差值推导两个干涉信号之间的光程差。实验结果证明了分辨率超过相干长度3 倍的可能性,测量误差小于10 %,相信该方法有利于波导元件结构和反射特性的研究、短光纤拍长值的测量等。但是,该方法仍然存在需要改进的地方,如计算过程复杂、计算过程中会存在多解的可能性、测量精度不高等。
