整体式U 型混凝土渠道衬砌-冻土接触模型

王玉宝，吴浩兴，刘 荣，白雅文，程森浩，张晨昊，周仁宇

（1. 西北农林科技大学旱区农业水土工程教育部重点实验室,杨凌 712100；2. 西北农林科技大学旱区节水农业研究院,杨凌 712100）

0 引言

整体式U 型混凝土衬砌渠道是国内常见的输水渠道，而在中国北方寒区存在大量冻土，其不均匀冻胀使渠道衬砌结构产生破坏。因此，研究渠道工程的冻胀破坏问题，提出相应的抗冻胀措施，对于保障渠道正常输水与使用寿命具有重要意义。

当地面温度持续处于负温时，地表土层发生冻结且冻结锋面逐渐向深层发展。冻土层的土壤水在土水势作用下向冷端迁移使基土发生冻胀现象[1-2]。渠道衬砌对基土的不均匀冻胀变形产生约束，进而在衬砌与基土之间产生冻胀力，是导致衬砌破坏的主要原因[3]；混凝土衬砌自身的抗拉和抗弯能力较差也使其易受到破坏[4-5]。以往许多研究在模拟与分析渠道冻胀破坏时，将渠道冻胀模型中的衬砌与基土看作整体，忽略了两者接触面间存在的相互作用[6-9]。王羿等[10]通过室内渠道冻胀试验发现渠基土冻胀量与衬砌位移不匹配，基土与衬砌间存在分凝冰层及脱空现象；孙厚超等[11-12]通过接触力学试验探究了接触界面的剪切力学特性，认为接触层具有约束作用。这说明在衬砌-冻土接触面间存在冻结约束、分离及摩擦滑动等多种接触关系，直接影响着接触面间的相互作用力。基于此，随后的研究将衬砌与渠基土视为两种不同的组件结构，探究衬砌-冻土的接触作用[13-18]。一些学者依据渠道冻胀破坏模型，分析了衬砌与基土的非线性接触关系[19]，建立了有冻土与衬砌接触作用的渠道冻胀破坏模型。这些模型将该接触作用简化为法向力与切向力，通过数值模拟分析衬砌受力破坏特征[20-21]。然而，这些模型中的衬砌-冻土接触研究仍存在不足：模拟多采用稳态分析，对接触面间的分离和滑动过程的分析不深入；衬砌-冻土接触模型缺少室外试验的验证。

针对以上不足，本文以内蒙古河套灌区整体式U 型混凝土渠道室外试验为原型，将混凝土衬砌与渠基冻土按照考虑衬砌-冻土接触作用和不考虑衬砌-冻土接触作用两种情形构建模型，采用有限元仿真软件ABAQUS 模拟两种模型的渠道冻胀破坏过程。通过试验监测的基土温度场、分层冻胀量和土压力等数据对比评估两种模型的合理性，分析渠道衬砌的受力状态与破坏机理。综合试验数据和模拟结果，解析衬砌-冻土分离、滑动过程对渠道冻胀破坏的影响。

1 力学模型的建立

1.1 热分析

基土温度降低至负温是引起土体冻胀的首要因素。热量的传递方式主要有3 种：热传导、热辐射和热对流。一般地，基土中热辐射和热对流传递的热量极少，引发的温度变化可以忽略不计。本研究模型未直接添加水分场，将水分场的影响反映在试验反演的基土冻胀系数中，因此热分析主要考虑由热传导引起的热量传递，忽略基土冻结过程中的水冰相变潜热释放和水汽蒸发、水分迁移等引发的热量。由于基土冻结过程的持续时间较长，且渠道工程的横向长度远小于其纵向长度，因此将该过程视为二维平面应变的瞬态热传导问题，由参考文献[19,22]确定热传导控制方程为

式中T为土壤温度，℃；λx、λy为冻土在x、y方向的导热系数，W/(m·℃)；A为模拟冻胀区域，m2。

1.2 材料本构模型

土体的冻胀强度受土壤含水率、密实度及地下水位高度等多种因素影响。本研究主要关注基土冻胀与衬砌接触面间的力学模型，土体冻胀位移通过试验反演得出的冻胀率计算。模型将冻土视作具有横观各向同性的弹塑性材料，其弹性模量随温度变化，冻土弹性阶段本构方程见式（2）～（4）[22-23]：

式中α为与温度相关的冻胀系数，1/K；T为土壤温度，K；T0为初始温度，K；εx、εy为x、y方向正应变；σx、σy为x、y方向正应力，MPa；τxy为剪应力，MPa；fβ为y方向坐标值，m；γxy为剪应变；E为弹性模量，MPa；ν为泊松比。

冻土塑性阶段满足广义Drucker-Prager 准则[24]：

式中p为等效围压应力，MPa；q为Mise 应力，MPa；c为黏聚力，MPa；b为内摩擦系数；pm为强度达到最大时的平均正应力，MPa。模型冻土塑性阶段采用ABAQUS 自带的线性Drucker-Prager 模型[25]，其屈服面函数为[22]：

式中F为屈服面函数；pa为平均应力，MPa；t为偏应力，MPa；β为屈服面在应力空间上的倾角，（°）；d为屈服面在应力空间t轴上的截距，m。

混凝土衬砌结构在冻胀破坏过程中经常产生塑性破坏。为模拟混凝土材料的压缩和拉裂等力学性能，模型的衬砌采用ABAQUS 提供的的混凝土损伤塑性模型，其本构方程为

式中σ为应力模量，MPa；ε为应变模量，MPa；d'为材料刚度损伤变量；为初始材料弹性刚度，N/m；为材料损伤后弹性刚度，N/m；上标“el”表示弹性状态；上标“pl”表示塑性状态。

1.3 衬砌-冻土接触本构

渠道衬砌-冻土接触面间的相互作用相当复杂。在不考虑接触模型中将渠道衬砌与基土在同一模块建模且视作整体，将衬砌与冻土沿接触面设置固定约束；在模拟过程中衬砌与冻土间可传递温度与应力，无相对位移发生。考虑接触模型中设置了衬砌与冻土间的接触力学行为，将接触作用简化为法向接触作用和切向接触作用。法向接触采用ABAQUS 中的修正硬接触模型，接触面在分离前可以承受一定的拉应力，其拉应力极限值为最大法向胶结强度Pmax，当接触应力超过该极限值时，衬砌与冻土发生分离，接触面间无热量与应力传递[26]。根据现场试验监测情况，渠底处衬砌与基土在脱离前达到的最大法向应力值为2 kPa，因此本模型取最大法向胶结强度Pmax=2 kPa。

切向接触采用ABAQUS 中的修正库伦摩擦模型[27]，在渠基冻土与衬砌的接触面间的临界剪切应力称为冻结强度。当接触面的切向应力小于冻结强度时，认为接触面处于粘结状态；当切向应力达到冻结强度后，认为接触面发生相对滑移。冻结强度与土壤水分、温度、土体类型和接触材料等因素相关[28]，其计算经验公式[29]为

式中τmax为衬砌-冻土接触面间的冻结强度（临界剪切应力），kPa；c为黏聚力，在此取c=0.4 kPa；m为与土质相关的系数，在此根据本文试验情况取m=1 kPa/℃；t1为负温绝对值，℃。在切向接触模型中，未达到冻结强度的剪切应力遵循库伦摩擦定律[26]，其计算公式为

式中τ为衬砌-冻土接触面间的剪切应力，MPa；μ为与温度相关的摩擦系数，根据以上计算所得冻结强度与试验监测法向应力极值，经计算取μ=0.7；P为衬砌-冻土接触面间的法向应力，MPa。

2 渠道模型及参数处理

2.1 现场试验概况

在内蒙古河套灌区曙光试验站布设室外试验，修建长10 m 的整体式U 型渠道，采用C15 混凝土衬砌。当地土质为砂壤土，天然含水率约为6%～10%，干密度约为1 600 kg/m3，地下水位深度约为0.6 m。土体冻结期在12 月16 日至次年3 月20 日左右。渠道断面设计和试验具体布设如图1 所示，渠道实测冻胀资料见表1。渠道顶部开口96 cm，渠深79 cm，设计水深64 cm，衬砌厚度8 cm，竖直倾角10°，渠底圆弧段半径40 cm，设计流量为0.261 1 m3/s。

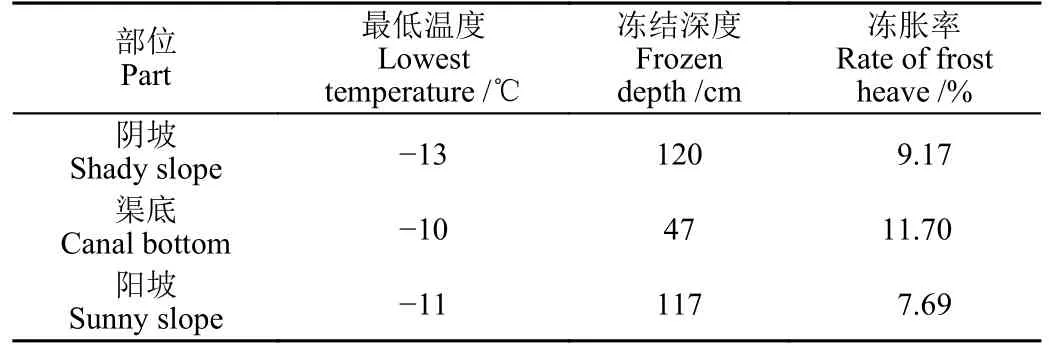
表1 渠道实测冻胀数据Table 1 Measured frost heave data of the canal

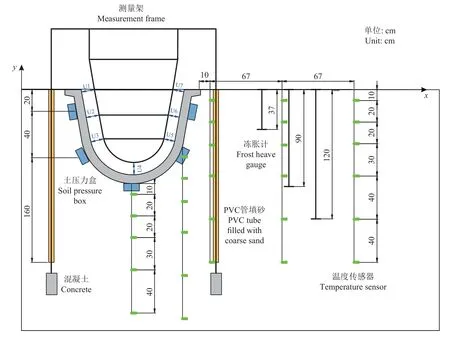
图1 现场监测试验布设横剖面图Fig.1 Local monitoring experimental layout cross section diagram

试验监测内容包括基土温度场、渠道下表面土压力、基土分层冻胀量和衬砌表面冻胀量。在渠道下方和旁边基土布设5 列共29 个温度传感器以监测基土的温度分布情况。为监测渠道所受土压力，在衬砌下表面布设5 个土压力盒，分别位于垂直地面-20、-60 和-87 cm（渠底）处。为监测基土冻胀量，在地表面和垂直地面-37、-90 和-120 cm 处布设冻胀计，由不同冻胀计间的位移差推算土层冻胀量。在渠道表面安装一个固定在基岩上的衬砌位移测量架，以测量架为基准量取渠道表面不同测点（U1～U7）的冻胀量。

2.2 有限元模型及参数选取

2.2.1 有限元模型

有限元模型及其网格划分如图2 所示。模型的边界参考当地环境条件和试验数据选取。试验中，垂直地面方向的最远端温度传感器的埋深为2.07 m，水平方向的最远端传感器距离阳坡渠顶1.45 m。因此，模型的下边界FG 取距离坐标原点A 点-2.07 m 的恒温层，右边界EG取距离A 点4.11 m，阴、阳坡渠顶B、D 距离A 点距离为1.45、2.66 m。不考虑接触模型将渠基土与衬砌当作整体建模，两者在模拟过程中处于接触状态，可以传递热量与应力，但无分离与相对滑动等接触作用发生；考虑接触模型将基土和衬砌分别建模，再沿接触面将两者进行装配。模拟时长取基土开始发生冻胀（12 月16 日）至其冻胀量达到最大值（次年2 月14 日）的时期，共60 天。网格单元采用四节点热力耦合平面应变四边形单元，共划分8 038 个单元。模拟采用瞬态分析求解，通过热力耦合的方法模拟基土冻胀和渠道破坏过程。

图2 整体式U 型渠道有限元网格划分Fig.2 Finite element meshing of integral U-shaped canal

2.2.2 边界条件

模型的温度边界根据试验监测数据确定，取渠道表面各处的最低温度作为温度条件。如图2 所示，阳坡BC 的表面温度取-11 ℃，阴坡DC 的表面温度取-13 ℃，渠底C 处的表面温度取-10 ℃，地面AB 和DF 的表面温度取-14 ℃。左右边界AF 和EG 设置为绝热边界。下边界FG 为恒温边界，其温度取4 ℃。受周围基土的约束作用，模型的左右边界设置水平位移约束，下边界设置竖向位移约束，上边界不设置约束。衬砌与基土间设置接触边界，其边界条件根据接触模型进行设置。

2.2.3 材料参数

热学参数：查阅文献[30]，由基土含水率线性插值，得到渠基土的热传导率 λ1=0.8 W/(m·℃)，由文献[31]查得混凝土的热传导率 λ2=2.3 W/(m·℃)。渠基土的比热容C1=0.92 kJ/(kg·℃)，混凝土的比热容C2=0.97 kJ/(kg·℃)。

力学参数：根据试验土壤测定数据，渠基土密度取1 600 kg/m3。基土冻胀系数由本文试验反演得到，将基土冻胀系数与温度进行拟合，拟合公式如式（10）、式（11）。

式中αy为y方向上的冻胀系数，αx，z为x、z方向上的冻胀系数，T为土体温度，K。基土弹性模量E、剪切模量G和泊松比等具体弹性参数见表2[23,31-32]。基土塑性部分采用线性Drucker-Prager模型，其具体参数为：内摩擦角φ=16.7，流变应力比k=0.8，剪胀角 ψ=8°[23]。根据《混凝土结构设计规范》（GB50010-2010），C15 混凝土的密度取2 400 kg/m3，弹性模量取22 GPa，泊松比为0.167。

表2 渠基土材料弹性参数Table 2 Elasticity parameters of canal foundation soil material

3 结果与分析

3.1 渠基土温度场分布

不考虑接触模型与考虑接触模型设置的边界温度和热传导系数相同，因此两者的模拟基土温度场基本相同。以考虑接触模型的计算结果为例，基土温度场分布如图3所示。模拟所得的左侧阴坡渠顶最大冻深为1.23 m，右侧阳坡渠顶最大冻深为1.19 m，渠底最大冻深为0.45 m。由于试验地区昼夜温差较大，而模拟的的温度边界仅根据试验最低温度设置温度梯度，因此温度场存有一定误差。相较于表1 的试验数据，模拟的阴坡冻深增大了2.44%，渠底冻深减小了4.26%，阳坡冻深增加了1.68%，模拟结果比较符合试验监测结果。

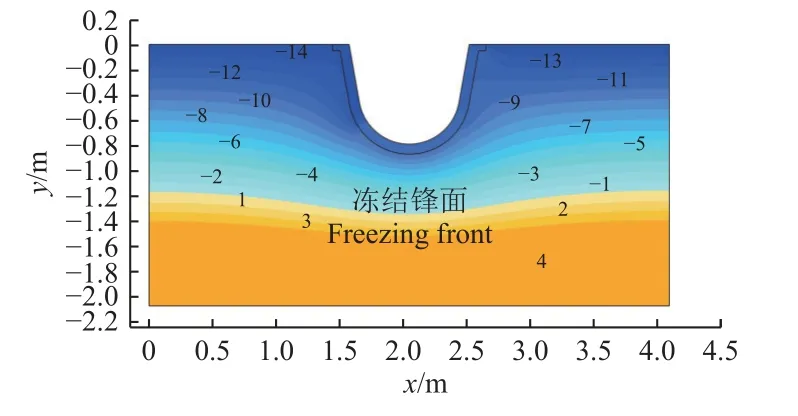
图3 考虑衬砌-冻土接触模型的基土温度场（单位:℃）Fig.3 Subsoil temperature field using considering lining-frozen soil contact model (unit: ℃)

3.2 渠基土法向冻胀量与渠道衬砌法向冻胀量

渠基土的冻胀量主要受土壤温度、含水量及土质影响，这些影响包含在反演的冻胀系数中。然而，图4 显示衬砌和基土接触面间的接触作用对基土的冻胀发展有轻微的影响。考虑接触、不考虑接触模型的0～37、＞37～90 cm 土层冻胀量和地面冻胀量与试验观测值的平均相对误差见表3。相比不考虑接触模拟，考虑接触模拟值与试验值基本接近。受昼夜温差大的影响，试验的0～37 cm 土层冻胀量波动较大；而模拟的该处温度变化缓慢，冻胀量模拟误差较大。图5 为放大5 倍后的考虑接触模拟终期的基土法向冻胀量。基土开始冻胀后，渠底衬砌与基土发生分离，渠底衬砌的拉应力消失。在衬砌板的力矩作用下，渠坡与渠顶板处的基土受衬砌的压迫变强。因此，相比于不考虑接触模型，考虑接触模型对渠坡基土冻胀产生了微弱的限制作用。

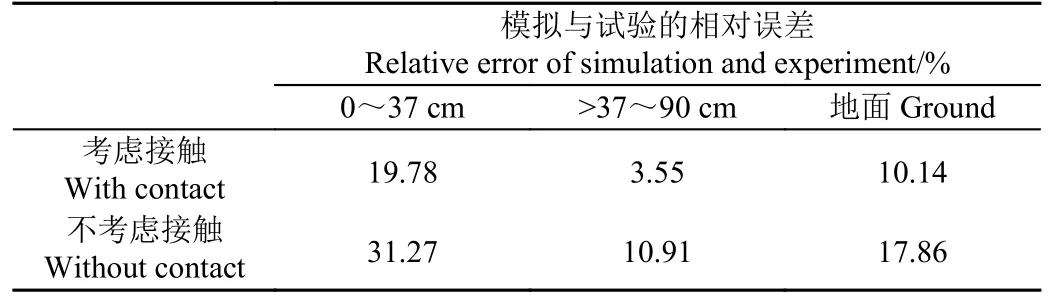
表3 模拟与试验的冻胀量对比Table 3 Comparison of frost heave displacement between simulation and experiment

图4 基土分层法向冻胀量及地面冻胀量Fig.4 Normal frost heave displacement of stratified subsoil layer and ground

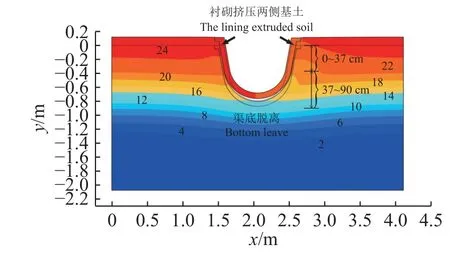
图5 考虑衬砌-冻土接触模型的基土法向冻胀量：放大5 倍单位:mmFig.5 Subsoil normal frost heave displacement of considering lining-frozen soil contact model: zoom in 5× unit : mm

渠道衬砌的法向冻胀量常作为渠道结构的稳定性控制指标。现场试验、考虑接触模型与不考虑接触模型的衬砌最大法向冻胀量如图6 所示。试验与模拟的衬砌最大法向冻胀量均在工程允许范围内[33]。考虑接触模型与试验结果的平均相对误差为7.1%，不考虑接触模型与试验结果的平均相对误差为13.9%；相比于不考虑接触模拟结果，考虑接触模型的衬砌最大冻胀量更符合现场试验监测情况，考虑接触模型可以较好地描述衬砌冻胀位移情况。相对滑动等接触作用对衬砌冻胀量有微弱的限制作用，符合基土法向冻胀量的发展规律（图4）。

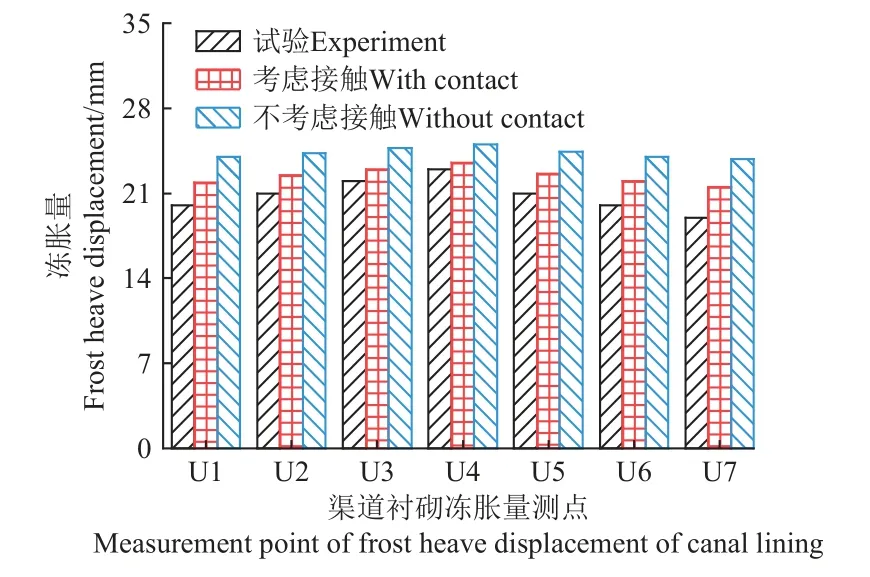
图6 渠道衬砌最大法向冻胀量Fig.6 The maximum normal frost heave displacement of canal lining

3.3 渠基土及衬砌应力

衬砌结构的变形和应力受衬砌-冻土接触作用的影响。接触作用表现为冻结时的相互约束力、冻结力达到极限时发生的渠底分离和渠坡滑移过程。根据试验土压力监测位置，取考虑接触与不考虑接触模型的两边坡-20 cm、-60 cm 处以及渠底-87 cm 处的基土法向冻胀力变化情况，与试验观测结果对比如图7 所示。

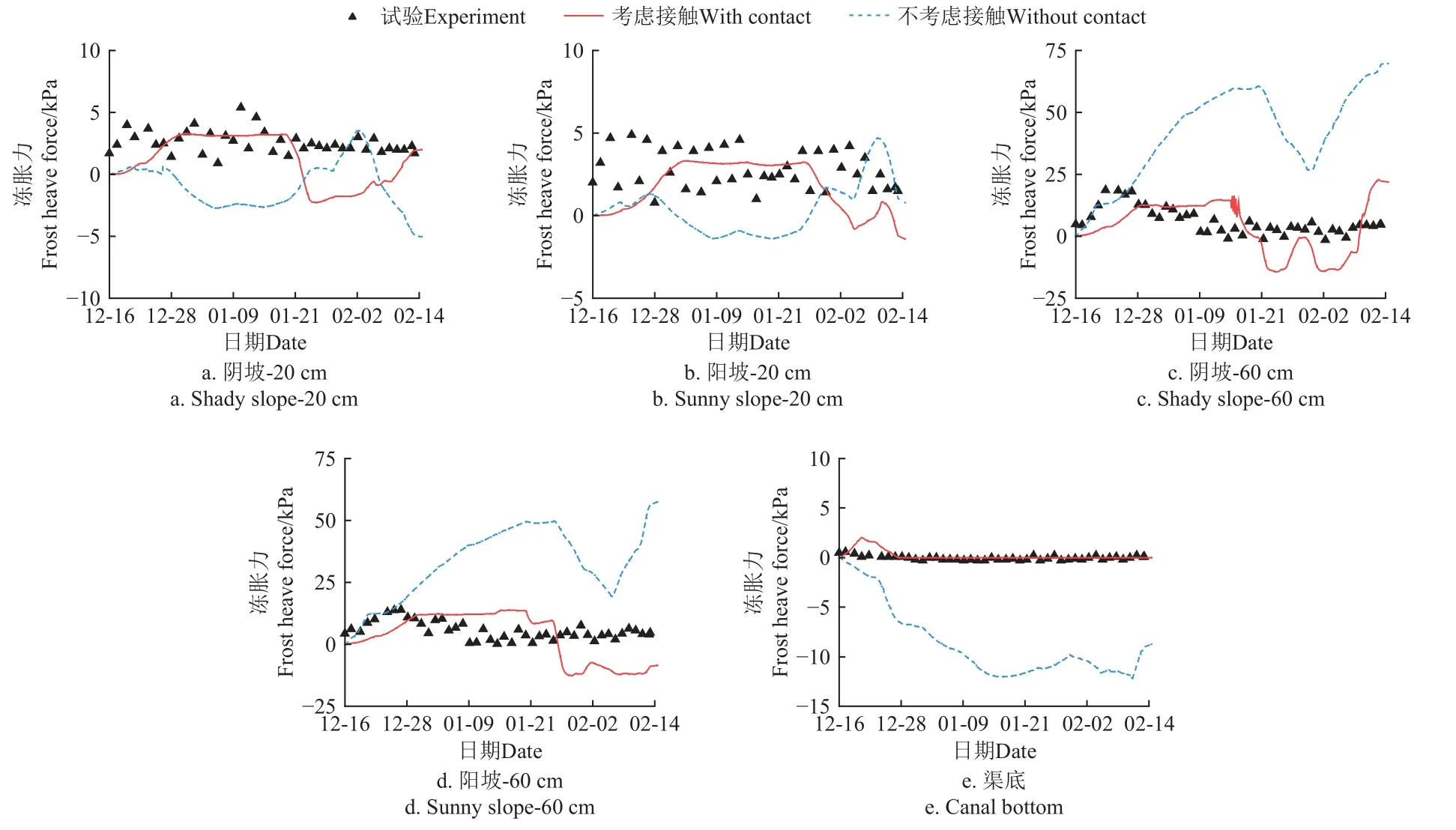
图7 渠道不同位置的基土法向冻胀力Fig.7 Subsoil normal frost heave force at different locations of the canal

两种模拟情景在-20 cm 基土处与试验观测值的差距较小。考虑接触模型的法向应力呈先压后拉的趋势，后期出现拉力的原因为阴、阳坡处基土先后达到塑性屈服状态使得衬砌结构发生偏转，加上衬砌-冻土的相对滑动，使顶部基土受拉后又重复受压。不考虑接触模型的衬砌与基土无法分开，坡顶衬砌板有向坡脚处转动的趋势，坡顶基土呈受拉状态；之后阴、阳坡处基土先后达到塑性屈服状态使冻胀变形减缓，两侧渠顶基土开始承受基土压力；最后在下部基土的顶胀作用下，两侧渠顶基土重复出现拉应力。

在-60 cm 基土处，试验应力呈先增大后减小最后保持相对稳定的规律。考虑接触模型应力峰值与试验应力最大值之间的误差约为10%，而不考虑接触模型应力峰值比前两者的峰值大3 倍左右。在考虑接触模型中，由于阴坡处温度梯度较大，阴坡-60 cm 处应力先于阳坡-60 cm处应力开始减小。当基土达到塑性屈服状态时，衬砌与基土有相互挤压的作用。之后，基土产生塑性破坏，衬砌与基土间发生相对滑动，短期内应力波动较大且基土有轻微塌陷，在模拟中后期有拉应力出现。不考虑接触模型中不存在冻结力破坏约束以及冻胀应力的释放过程，应力随基土冻胀持续增大，这造成了很大的模拟误差。

在试验中，由于上部基土先于渠底基土发生冻胀，在冻胀土体对衬砌的挤压抬升作用下，渠底衬砌与基土发生分离，无接触应力存在。由于底部衬砌悬空，渠坡处衬砌与基土发生变形。渠底衬砌在弯矩作用下发生破坏，渠底表面出现轻微的拉裂现象。考虑接触模型和试验监测的渠底基土法向冻胀力基本为0，而不考虑接触模型的渠底基土则一直处于受拉状态。考虑接触模型的基土在温度梯度的作用下，渠坡基土比渠底基土的冻胀变形更大，底部衬砌在渠坡基土的顶胀作用下与基土脱离，因此渠底接触应力在模拟时段内一直为0，这与试验监测情况一致。

衬砌的横截面应力强度是评价结构稳定性的重要指标。图8 为考虑接触模型和不考虑接触模型的衬砌表面最大正应力模拟值。衬砌上表面主要承受压应力，其中不考虑接触模型的最大压应力为2.37 MPa，出现在渠底偏阴坡处；同样出现在此处的考虑接触模型的最大压应力为0.24 MPa，其应力峰值削减了903%。衬砌下表面主要承受拉应力，且越靠近渠底中心其拉应力越大。与不考虑接触模型应力峰值相比，考虑接触模型的下表面应力峰值减小了164%。根据《混凝土结构设计规范》（GB50010-2010），C15 混凝土材料的极限压应力为10 MPa，极限拉应力为1.27 MPa。两个模型的渠底衬砌在模拟过程中都未达到极限破坏状态，与试验中渠底衬砌无明显破坏相对应。在渠道冻胀模型中增加接触作用后，衬砌与基土间存在摩擦和滑移过程。这些接触过程使衬砌应力在基土冻胀和衬砌变形过程中得到释放，与实际过程更接近。

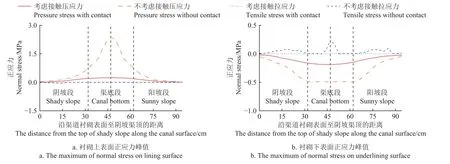
图8 渠道衬砌截面正应力峰值沿渠道表面分布Fig.8 The distribution of normal stress maximum of canal lining along the surface

图9 为衬砌表面切应力峰值，不考虑接触模型的最大切应力大于考虑接触模型的最大切应力，且两者均出现在渠底处。不考虑接触模型的切应力随基土冻胀而不断增大。考虑接触模型的最大切应力出现在渠底段，达到峰值的时间为底部衬砌与基土发生分离的临界点，冻结约束在此时破坏。

图9 渠道衬砌切应力峰值沿渠道表面分布Fig.9 The distribution of tangential stress maximum of canal lining along the surface

4 讨论

4.1 衬砌-冻土接触原理分析

本研究通过瞬态模拟，分析了考虑与不考虑接触模型的基土冻胀量、土压力和衬砌表面应力的变化过程。相比于不考虑接触模型，考虑接触模型的模拟结果更符合试验监测情况，这与前人试验与稳态模拟得出的规律相符[22,34-35]。以往的稳态模拟常聚焦于基土达到最终稳定状态的冻胀变形与应力；而瞬态模拟则可以实现基土冻胀过程的动态可视化，更能从时间角度研究与分析衬砌-冻土的相互作用过程和应力发展规律。

当模型考虑接触后，基土和衬砌的应力极值有较大削减。由图7，考虑接触模型的基土阴、阳坡-20cm 处应力极值分别降低了134%和41%，阴、阳坡-60cm 处应力极值分别降低了206%和334%；衬砌上表面应力峰值降低了903 %，下表面应力峰值降低了164%，切向力峰值降低了248%。此外，考虑接触会明显改变应力的发展趋势，其发展由“增力”变为“卸力”。不考虑接触模型的基土应力极值与最大冻胀量总出现在模拟终期（图7）；而考虑接触后，基土应力会有不同程度的消减，极值会提前至中后期（图10），这也与试验情况相符合。

衬砌与冻土的相对滑动过程释放了接触面间的作用力，导致衬砌冻胀量与基土压力的极值错开。由瞬态模拟可对该滑动过程进行讨论分析。由图10，衬砌与冻土在A 点处于相对滑动临界点，此时衬砌-冻土处于粘结状态，接触面间存在受约束的法向冻胀力和切向冻结力。发生滑动后，接触面间原本受约束的法向冻胀力被释放，法向应力逐渐减小；滑动过程使衬砌与基土间产生剪切作用，接触面间的剪切位移增加，剪应力随之增大。考虑接触模型的滑动过程可视为接触面间的摩擦作用，切向应力与法向应力呈正相关。随着衬砌与基土的摩擦作用，接触面上的法向应力与切向应力逐渐减小，出现“卸力”的情况。

4.2 接触模型的工程应用

基土冻胀和衬砌-基土接触约束是渠道冻胀破坏产生的必要因素。当基土冻胀强度不足或衬砌与基土间的约束力被释放时，衬砌都无冻胀破坏发生。在寒区渠道工程中，常采用基土换填、铺设保温板和防渗排水等措施以削减基土冻胀，减少冻土对衬砌的挤压破坏[36]。从衬砌-基土接触约束的角度，在衬砌与基土间铺设土工膜可以改变衬砌与基土间的约束关系，削减基土等效应力[37]。一个弱的约束关系会更有利于渠道衬砌在基土冻胀过程中的应力释放。

根据本研究的结果，考虑接触模型更符合实际的渠道冻胀破坏情况，可以进一步用于合理地模拟工程措施的抗冻胀效果。例如，通过调整模型中的基土材料参数和温度边界条件等，可以模拟置换基土与蓄热保温等措施的抗冻胀效果。通过改变模型的渠道断面形状，可探究不同断面形式的应力分布与易发生破坏的位置，从而针对易破坏点采取抗冻措施。此外，本模型可以进一步用来探讨不同接触模式对衬砌-冻土相互作用的影响程度，比较不同接触情况下的衬砌受力和冻胀破坏情况。比如，布设土工膜后，原模型的衬砌-冻土直接接触转变为衬砌-土工膜-冻土的间接接触。其法向模型中仍可采用硬接触方法计算；切向接触模型则应将库伦摩擦模型更改为适用于模拟粘结界面脱粘的内聚力模型。

5 结论

针对中国北方寒区的渠道冻胀破坏问题，本文以整体式U 型渠道冻胀破坏监测试验为原型，建立了考虑接触和不考虑接触冻胀模型。通过试验数据对比验证了考虑接触冻胀模型模拟的准确性，分析了基土与衬砌的应力状态和衬砌-冻土的分离、滑动过程，得出以下结论。

1）考虑接触模型模拟结果极大降低了不考虑接触模型模拟的土压力误差。考虑接触、不考虑接触模型与试验的温度场分布基本相同，土层法向冻胀量与衬砌法向冻胀量差距较小。在边坡处，考虑接触模型的法向土应力变化趋势与极值都与试验监测值基本符合；而不考虑接触模型的法向土应力极值可达前两者的3.3 倍。在考虑接触模型与试验中，渠底处法向土应力基本为0；不考虑接触模型中则存在持续增大的拉应力。

2）结合考虑接触模型与试验，可使衬砌-冻土接触面间的分离与滑动过程动态可视化。冻胀开始后，由于基土冻胀的不均匀性，渠底衬砌与基土率先发生分离，无接触应力传递。之后，边坡处衬砌与冻土发生相对滑动，原本被约束的衬砌应力得到释放。在应力释放过程中，衬砌冻胀量仍在不断增大。

3）滑动过程改变了应力发展趋势，其发展由不考虑接触的“增力”变为考虑接触的“卸力”。与不考虑接触模型相比，考虑接触模型在模拟滑动的释放力作用下，衬砌上下表面正应力峰值分别降低了903%和164%，下表面切应力峰值降低了248%。应力峰值均出现在渠底略偏阴坡处，该处更容易发生破坏。