基于改进多目标遗传算法的农村低碳物流配送路径优化

宾 厚 张路行 王素杰 王欢芳

(湖南工业大学 商学院,湖南 株洲 412008)

随着国家乡村振兴战略的深入推进,农村物流日益成为推动农村经济社会发展的关键要素。《2021年中国快递发展指数报告》[1]调查数据显示:2021年,我国农村地区收投物流快件量超过370亿件,带动农村经济增长超过1.85万亿元,农村物流市场的发展日益繁荣。《商务部、国家邮政局等八部门关于加快贯通县乡村电子商务体系和快递物流配送体系有关工作的通知》[2]指出:要加快形成以县级物流配送中心、具有集散功能的乡镇网点和村级寄递物流综合服务站为主体的农村快递物流配送体系。然而,由于我国农村地区具有地形和地势复杂,物流基础设施不健全,交通跨度大,物流需求不确定且主体分布分散等一系列发展特征,农村物流配送尤其是乡镇到各村落的末端配送问题十分突出,“最后一公里”物流配送产生的成本占比整个物流环节的35%～60%[3]。与此同时,农村物流企业也面临着物流网络不健全、配送路径规划不合理、信息化水平低、服务质量较差、快件的时效性难以保证等一系列问题,这为我国农村物流企业的高质量发展提出了新挑战[4]。此外,农村物流作为连接“农产品上行”和“工业品下行”的双向流通渠道,也面临着高污染、高能耗、配送效率低下等问题,如何实现农村物流的低碳发展和降本增效成为当前亟需解决的关键问题。在国家“碳达峰、碳中和”战略背景下,农村物流配送路径优化对于降低物流能耗、提升物流运作效率以及减少CO2排放量至关重要。基于此,深入研究需求不确定和碳排放约束的农村物流配送路径优化问题对于促进我国农村经济向低碳化转型、实现高质量发展具有重要现实意义。

近年来,国内外相关研究主要涉及以下3个方面:1)需求不确定的物流配送路径优化问题。赵燕伟等[5-7]分别构建一系列物流配送路径优化模型,并分别采用量子进化算法、遗传算法、杂草优化算法等对模型进行求解。姚源果等[8]应用交通大数据,以总成本最小化为目标,采用蚁群算法对农产品冷链物流配送路径优化问题进行深入探究。Yao[9]以降低物流配送成本、减少物流配送车辆数量为目标,构建了带时间窗的农村物流路径优化模型,并采用遗传算法对模型进行求解。Teodorovic等[10-11]结合模糊集合理论,分别构建需求不确定和有追索权的随机物流配送路径优化模型,并采用模拟退火算法、遗传算法和局部搜索算法对模型进行求解分析。Lorini等[12-15]针对具有动态需求和动态行驶时间的车辆路径问题,提出对新客户优先设计配送路径的原则,分别构建了随机需求和随机服务时间的车辆路径优化模型,并设计出禁忌搜索算法和蚁群算法进行求解。2)碳排放约束的物流配送路径优化问题。Kim等[16]、Çimen等[17]和Brandstatter等[18]结合碳排放约束与物流配送路径优化之间的关系,构建相应的物流路径优化模型,并分别采用蚁群算法、模拟退火算法以及粒子群算法对模型进行求解。Marcel[19]则是以车辆路径问题(Vehicle routing problem,VRP)为原型,以降低物流配送油耗和碳排放规模为目标,建立生鲜农产品低碳物流路径优化模型。方文婷等[20]构建综合考虑低碳、时效和成本节约的带时间窗动态需求物流路径优化模型,并设计蚁群启发式算法对模型进行优化求解。任腾等[21-22]分别构建包含碳排放成本、货损成本、时间成本和客户满意度等要素的农产品冷链物流路径优化模型,并分别采用蚁群算法和混合遗传—禁忌搜索算法对模型进行求解分析。李军涛等[23]针对冷链物流配送成本较高和车辆利用率低的问题,利用投入产出法计算出车辆运输过程中的碳排放量,构建了带时间窗的冷链物流路径优化模型,并采用自适应遗传模拟退火算法对模型进行求解。3)同时考虑需求不确定和碳排放问题。其中,裴利奇等[24-25]分别对不确定需求下的快递中转站和低碳物流配送中心选址问题进行研究,发现用户的需求不确定对物流选址和碳排放量具有显著影响。张倩等[26]综合考虑配送成本、生鲜产品生鲜度、碳排放和客户的随机需求等因素之间的关系构建了生鲜电商配送路径规划模型,并应用主要目标法和果蝇算法对模型进行求解。张旭等[27]则是从需求和碳交易价格双重不确定的多式联运路径优化问题出发,建立了混合鲁棒随机优化模型,研究发现需求不确定的最大遗憾值与成本之间的关系是提升双重不确定下多式联运运输效率与环保效益的有效方式。邓学平等[28]采用混合时间窗约束以成本和碳排放量最小化为目标构建了不确定需求下的多式联运路径优化模型,并采用基于模拟退火的粒子群算法对模型进行求解。

综上,关于物流配送路径优化问题的研究成果主要存在以下不足:第一,已有研究大都基于城市地区物流配送路径优化问题展开,同时考虑需求不确定和碳排放约束的农村物流配送路径优化问题的研究成果相对匮乏。第二,相关研究大多集中于单一车型的配送路径优化问题,与农村物流企业多车型配送的现实应用场景有偏差。第三,已有研究中对模型的求解大多采用传统的遗传算法、蚁群算法、模拟退火算法等算法,而这些算法由于全局搜索能力不足容易陷入局部最优解。针对以上问题,本研究旨在考虑需求不确定和碳排放双重约束下构建包含需求覆盖率、距离成本、时间惩罚成本、碳排放成本、固定成本等要素的农村物流配送路径优化模型,设计适用于多车型的改进多目标遗传算法,同时应用农村物流配送数据进行仿真试验,将传统遗传算法和改进多目标遗传算法的结果进行对比分析,最终得出农村物流的最优配送方案,以期实现需求覆盖率最大化、碳排放和配送成本最小化的目标。

1 问题描述与假设条件

1.1 问题描述

结合农村物流运作的实际情况,主要研究分布在县城区域的农村物流配送中心给各个乡镇及村落的多个配送网点配送快递包裹的农村物流配送路径优化问题。设定农村物流配送中心拥有n辆多种型号的物流配送车辆,专门为多个物流配送网点提供生鲜农产品和物流快件的配送服务,配送车辆每天统一从配送中心出发,完成对各个配送网点配送作业的同时,并揽收需要上行的快件后再返回到配送中心。物流配送路径优化的目标是按照现有的资源条件和客户需求情况,构建满足需求不确定和碳排放约束的农村物流配送路径优化模型,并设计出适用于多车型的多目标遗传算法对模型进行求解,进而获取需求不确定和碳排放约束的农村物流最优配送路径,使得各配送车辆能够以最少的配送成本和最低的碳排放量完成配送任务,实现需求覆盖率最大化、碳排放和配送成本最小化的目标。

1.2 假设条件

为进一步说明农村物流配送路径优化问题,真实反映农村物流配送的现实情况,特设定以下假设条件:1)只有1个物流配送中心且具有多种车型的配送车辆。2)配送中心位置已知。3)各种车型的配送车辆核定载重量、配送成本不同。4)配送车辆从配送中心出发,在完成相关作业流程后返回到配送中心。5)已知各农村物流配送网点的位置、物流需求量、服务时间窗以及具体所需的服务时间。6)配送车辆的载重量不能超过其核定载重量。7)每辆配送车辆可服务多个配送网点但每个网点只能被1辆配送车辆服务1次。8)配送车辆超过配送网点的服务时间窗到达需支付一定的时间惩罚成本。9)所有配送车辆在配送过程中均匀速行驶。10)配送车辆的碳排放量和载重量、配送距离之间成正比。11)每条配送路径上的路况保持一致,不影响配送时间。

2 农村物流配送路径优化模型构建

本研究在考虑需求不确定和碳排放的双重约束下,以需求覆盖率最大化、碳排放和配送成本最小化为目标构建了包含需求覆盖率、碳排放成本、距离成本、时间惩罚成本等多要素的目标函数模型,同时设定满足车辆载重量限制、配送车辆限制以及配送时间限制等约束条件,使得多种不同型号的配送车辆从配送中心出发,向各个物流配送网点提供配送服务,完成配送任务后返回配送中心。

2.1 参数设定

为将农村物流的现实配送过程转化为具体的数理模型,需要对部分参数进行注释说明,本研究在构建需求不确定和碳排放约束的农村物流配送路径优化模型所使用的参数符号及定义见表1。

表1 本研究的参数符号及定义Table 1 Parameter symbols and definitions in this study

2.2 变量分析

2.2.1碳排放成本

为追求碳排放最小化的配送路径优化目标,本研究考虑将碳排放成本作为物流配送路径优化模型的重要组成部分,其中,碳排放成本主要包含配送过程中产生的燃油成本和碳税成本,由于碳排放成本和配送距离、载重量之间成正比,不同车型的碳排放量之间也有所差异,本研究配送车辆的碳排放量采用负载估计法计算得出。当m型配送车辆载重量为Q时,单位距离的碳排放量ρ(Q)为[20]:

(1)

式中:ρ0表示配送车辆的载重量为0时,单位距离的碳排放量;ρ*表示满载时配送车辆的碳排放量;Cm表示m型配送车辆的最大承载量;c为燃油价格;δ为碳税价格。

碳排放成本C1具体可用单位距离的燃油成本ps与单位距离的碳税成本pn之和乘以配送网点i与j之间的配送距离di,j表示:

(2)

2.2.2时间惩罚成本

结合农村物流配送过程现实情况,由于配送时效性对于农村物流企业的服务质量和客户满意度均有所影响[5],因此本研究考虑将时间惩罚成本作为目标函数,以此来增强农村物流配送的时效性,提升农村物流企业的服务质量和客户满意度。假定配送网点i的服务时间窗为[ei,li],配送网点i的时间惩罚成本C2的表达式为:

(3)

式中:β为时间惩罚系数;wi为配送车辆在配送网点i的开始服务时刻;li为配送网点i的时间窗结束时刻。

2.2.3需求覆盖率

需求覆盖率可表示为每条配送路径上的需求量和配送网点总需求量的比值,需求覆盖率越大说明配送路径的规划越合理,对客户需求的满足程度也就越高,提高农村物流的需求覆盖率可以有效提升农村物流运作效率,增强客户满意度。配送网点i的需求覆盖率Z的表达式为:

(4)

式中:pi为配送网点i的配送量;qi为配送网点i的取货量;yi,k为决策变量。

2.3 模型公式

2.3.1目标函数

由于农村物流具有“长配送链+低消费需求”的特征,本研究主要结合农村物流配送现实情况,以需求覆盖率最大化、碳排放和配送成本最小化为目标并考虑需求覆盖率和碳排放成本、固定成本、时间惩罚成本、距离成本等要素对农村物流配送路径优化的影响效应,构建了考虑需求不确定和碳排放约束的农村物流配送路径优化模型。其中,农村物流路径优化模型目标函数的表达式为:

(5)

2.3.2约束条件

结合农村物流配送的实际运作情况,本研究分别从配送车辆限制、载重量限制、配送时间窗约束等多方面设计了农村物流配送路径优化的约束条件。

1)保证配送中心每种类型配送车辆使用数量不超过此类型车辆可用数量的约束条件为:

(6)

2)所有配送车辆均从配送中心出发并且返回配送中心的约束条件为:

(7)

3)保证每个配送网点只被服务1次的约束条件为:

(8)

4)配送车辆在服务配送网点i后,到达下一个配送网点或回到配送中心的约束条件为:

(9)

5)每条配送路径上的需求量不高于此路径上配送车辆最大载重量的约束条件为:

(10)

6)配送车辆运作时间不超过服务时间最大值的约束条件为:

(11)

7)消除子路径约束的约束条件为:

(12)

8)配送服务时间窗的约束条件为:

ei≤ti≤li,i∈D

(13)

3 改进多目标遗传算法设计

由于农村物流配送路径优化问题属于NP-Hard难题,传统遗传算法对于求解单目标路径优化问题具有较好的适用性,但在求解多目标路径优化问题、尤其是要考虑到需求不确定和碳排放约束等多个约束条件时,求解效果会受到一定程度的影响。本研究主要参考李丹莲等[29]、赵赫等[30]的研究成果,基于遗传算法原理设计出适用于多车型的改进多目标遗传算法以求解需求不确定和碳排放约束的农村物流配送路径优化模型,可以有效避免无效解和非法解的产生,进而使得算法具有更优的求解效果,改进多目标遗传算法具体流程见图1。

图1 改进多目标遗传算法流程Fig.1 Improved multi-objective genetic algorithm process

3.1 染色体编码及初始化种群

本研究限制每辆配送车辆匹配1条配送路径,每个配送网点仅有1辆配送车辆进行配送服务,因此需要将配送网点、配送车辆以及配送路径进行编码处理。配送车辆序列初始染色体编码为:Sv={1,2,…,Kn},Kn表示可以使用的多车型物流配送车辆。配送路径的染色体编码为Sc={1,2,…,n},1表示农村物流配送中心,2,3,…,n表示各个配送网点。配送车辆染色体的序号表示可使用的配送车辆及其使用顺序,配送路径染色体序号表示需要提供配送服务的网点及其服务顺序。随后,将配送车辆染色体序列和配送路径染色体序列进行随机初始化,生成初始化种群,并以此为起点设置相关参数,进行遗传迭代。本研究配送车辆染色体和配送路径的染色体编码见图2。

图2 配送车辆和配送路径染色体编码Fig.2 Chromosomal coding of distribution vehicles and distribution route

3.2 适应度函数设定

适应度可以反映出种群中染色体的生存能力,适应度越大,代表染色体的生存能力越强,在遗传迭代过程中更容易被保留;当适应度越小时,代表染色体的生存能力较弱且容易在遗传迭代过程中被剔除。由于在农村物流配送路径优化模型中目标函数是求得需求覆盖率最大值和物流配送成本最小值,因此,本研究在设定适应度函数时选取需求覆盖率与配送成本的倒数之和作为适应度函数fi,适应度函数fi的具体公式为:

(14)

3.3 算法描述

3.3.1快速非支配排序

改进多目标遗传算法求解的关键是求取Pareto最优解集,通过快速非支配排序可以引导搜索过程不断向Pareto最优解集的方向靠近。对于种群P中的个体Pi,i=1,2,…,n,假设ni为种群中各支配个体Pi的个体数量,集合S代表被个体Pi支配的个体集合,φr为个体Pi的非支配序值,快速非支配排序的过程如下:

1)将种群中所有ni=0的个体放入到非支配集合F1中,并将其赋予相同的非支配序φr;

2)考察非支配集合F1中的每个个体Pi所支配的个体集合S,将集合S中每个个体Pj的nj都减去1,如果nj-1=0,j=1,2,…,n,说明个体Pj是S中的非支配个体,则将个体Pj放入另一个集合Q中,并对Q进行分层并赋予相应的非支配序;

3)对集合Q重复上述分层操作直到整个种群都被分层,并赋予不同分层相应的非支配序,同一分层内的个体非支配序φr相同。

3.3.2拥挤度

拥挤度代表种群中指定染色体周围其他染色体的密度,具体表示为指定点前后2条染色体之间目标函数差值之和。拥挤度越大,则染色体周围密度越小,染色体的多样性越好,反之拥挤度越小,则染色体周围密度越大,染色体的多样性越差。假定种群P中有n个个体和λ个目标函数,其拥挤度的计算过程如下:

1)设每条染色体i的拥挤度id=0,i=1,2,…,n;

2)对于每个目标函数F(xk)(k=1,2,…,λ),将种群中的所有个体按照目标函数值的大小排序;

3)计算种群中位于中间的非边界染色体拥挤度,拥挤度id的计算公式为:

(15)

式中:F(xk)max和F(xk)min分别表示第k个目标函数的最大值和最小值;F(xk)(i-1)和F(xk)(i+1)为染色体i前后两条染色体的第k个目标函数值。

3.3.3精英策略

改进多目标遗传算法的精英策略是为了保留父代种群中的优秀染色体,防止其在种群遗传迭代的过程中流失,从而提升算法的收敛性能。精英策略的具体步骤为:

1)将产生的子代种群Qt与父代种群Pt进行混合,形成新的种群Ut,种群大小为2n;

2)对种群Ut进行快速非支配排序,求出所有的非支配集Fi并分别计算每个非支配解集的个体拥挤度;

3)将F1放到新的父代种群Pt+1中,若此时种群Pt+1中个体数小于n,那么将非支配集F2放入种群Pt+1中,如果添加到非支配集Fn时,种群Pt+1个体数量超出n,则利用拥挤度对Fn中的个体选择,取前{num(Fn)-(num(Pt+1)-1)}个体,此时种群P的规模达到n;

4)采用遗传算法操作,从而产生新种群Qt+1。

3.4 染色体选择、交叉和变异

本研究染色体选择操作主要依据非支配排序φr和拥挤度id进行锦标赛选择,首先比较非支配排序φr,选择较小者。若φr相同,则比较拥挤度id,取较大者进入到下一部分的操作。染色体交叉操作主要采用部分映射交叉方法,具体流程见图3。

图3 染色体交叉流程Fig.3 Chromosomal crossover process

根据染色体变异概率对染色体进行变异操作,本研究主要采用2-opt算法分别对配送车辆和配送路径染色体进行变异操作,配送车辆染色体变异操作与配送路径染色体的变异操作方式相同,配送路径染色体的变异操作方式见图4。

图4 配送路径染色体变异操作方式Fig.4 Distribution route chromosome mutation operation process

4 仿真试验分析

4.1 数据来源

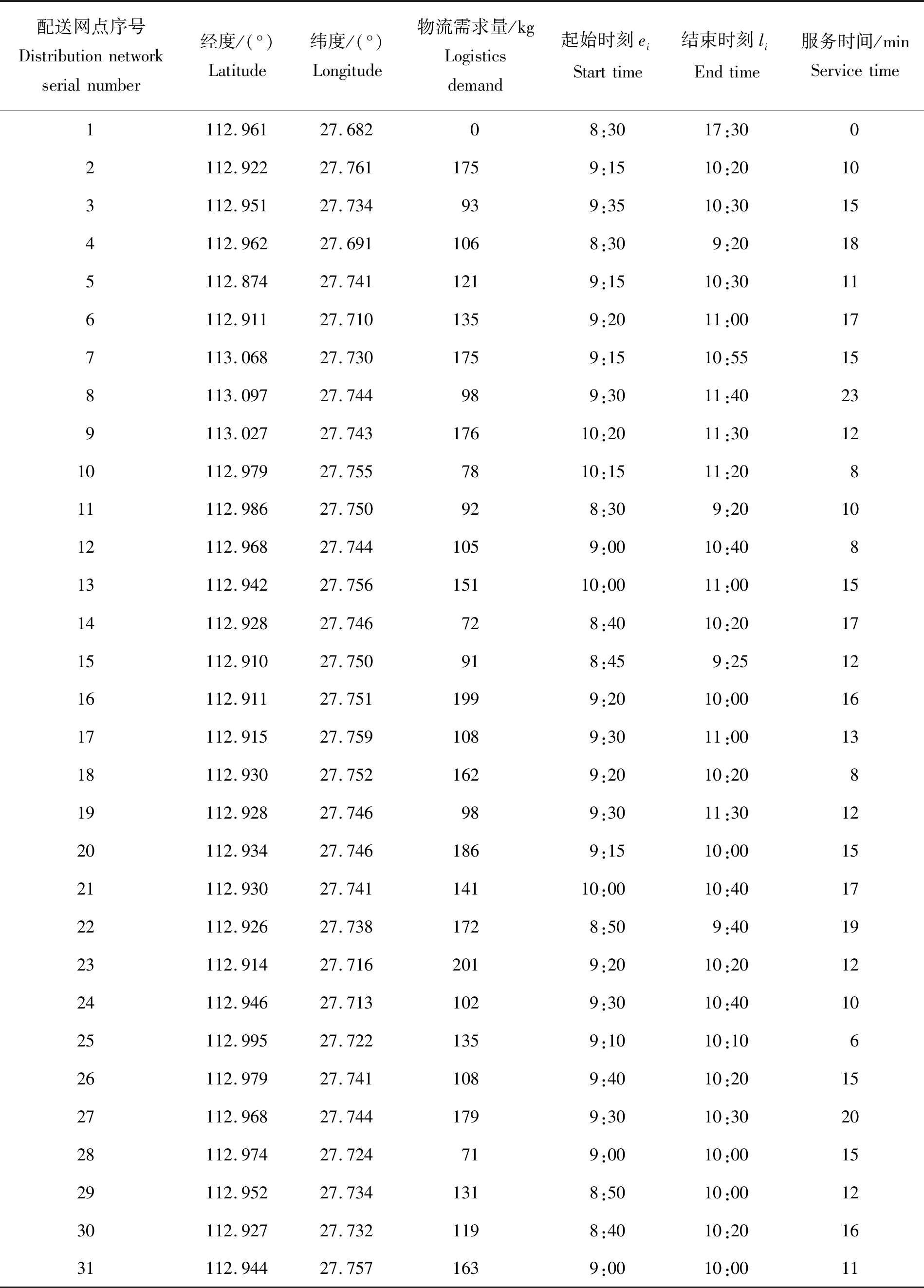
表2 配送网点的经纬度坐标、物流需求量、时间窗及服务时间Table 2 Latitude and longitude coordinates of distribution network,logistics demand,time windows and service times

(16)

(17)

4.2 仿真试验结果分析

本研究仿真试验中的配送车辆共分为A、B和C 3种车型,对应的车辆数分别为2、2和3,共7辆车。3种车型配送车辆的载重量分别为700、800和1 000 kg;固定成本分别为600、800和1 000元;单位距离成本分别为10、12和15元/km;单位距离的油耗分别为0.16、0.18和0.22 L/km;油价为8.52元/L;碳税价格为2.36元/kg;配送车辆匀速行驶的速度为40 km/h;超出时间窗的惩罚成本为300元/h。采用MatlabR2014a软件进行仿真,运用同样的试验条件和配送数据分别测试了20次。迭代轮数R取500,种群大小S取200,交叉概率Pc取0.75,变异概率Pm取0.2,测试后发现,与传统遗传算法相比,改进多目标遗传算法能够有效减少农村物流配送车辆使用数量,降低配送成本,提高需求覆盖率。因此,满足客户需求和降低碳排放并不冲突,寻求需求覆盖率和和碳排放规模的平衡有利于促进农村物流实现高质量发展,传统遗传算法和改进多目标遗传算法对目标参数的仿真结果见表3。

表3 传统遗传算法和改进多目标遗传算法对目标参数的仿真结果Table 3 Simulation results of traditional genetic algorithm and improved multi-objective genetic algorithm on target parameters

4.2.1单车型与多车型结果对比分析

为验证多车型配送方案在农村物流配送过程中的有效性和适用性,本研究分别对A、B、C 3种车型单独完成配送任务和3种车型同时完成配送任务进行了对比分析,研究发现采用多车型的配送方案比分别采用A、B车型的配送方案在配送成本分别降低了273.17元和585.88元,需求覆盖率分别提升了7.25%和0.87%,虽然单独采用C车型配送方案的需求覆盖率比多车型联合配送方案高1.62%,但是配送成本却高了1 141.12元,无法有效降低农村物流配送成本,与本研究所追求的需求覆盖率最大化、碳排放和配送成本最小化的目标有所相悖。由此可见,采用多车型联合配送方案在需求不确定和碳排放约束的农村物流配送中具有显著优势,单车型和多车型配送方案对目标函数值的影响见表4。

表4 单车型和多车型配送方案对目标函数值的影响Table 4 The impact of single and multi-vehicle distribution options on the objective function value

4.2.2需求覆盖率分析

为进一步探究需求不确定和碳排放约束下的农村物流配送路径优化问题,本研究分别采用传统遗传算法和改进多目标遗传算法对农村物流的需求覆盖率水平进行仿真试验。研究发现,采用改进多目标遗传算法与传统遗传算法相比,农村物流的需求覆盖率实现较大幅度增长。因此,本研究设计的改进多目标遗传算法对于求解需求不确定和碳排放约束的农村物流配送路径优化问题具有较强的适用性,能够有效提升农村物流的需求覆盖率水平。同时在仿真试验过程中发现,采用改进多目标遗传算法对模型进行求解比传统遗传算法提前120次左右目标函数达到收敛状态,有效节省了运算时间,算法的求解效率得到提升。由此可知,相对于传统遗传算法,本研究设计的改进多目标遗传算法对于求解需求不确定和碳排放约束下的农村物流配送路径优化问题具有更好的收敛效果,传统遗传算法和改进多目标遗传算法的需求覆盖率迭代过程见图5。

图5 传统遗传算法和改进多目标遗传算法的需求覆盖率迭代过程Fig.5 Iterative process of demand coverage for traditional genetic algorithm and improved multi-objective genetic algorithm

4.2.3配送成本分析

本研究涉及的农村物流配送成本主要包括碳排放成本、固定成本、时间惩罚成本以及距离成本(其他成本计算在固定成本中)。与传统遗传算法相比,应用本研究设计的改进多目标遗传算法进行仿真试验时目标函数配送成本的仿真值大幅度减少。因此,改进多目标遗传算法在求解农村物流配送路径优化问题时,能够有效降低农村物流配送成本,对解决农村物流配送问题具有较好的适用性和实际应用价值。同时在仿真试验过程中发现,在以配送成本最小化为优化目标时,采用改进多目标遗传算法比传统遗传算法目标函数达到收敛状态的时间有所提前。相比于传统遗传算法,改进多目标遗传算法对于求解考虑需求不确定和碳排放约束的农村物流配送路径优化模型具有更好的收敛效果,邻域搜索能力、求解稳定性以及算法性能也更优,传统遗传算法和改进多目标遗传算法的配送成本迭代过程见图6。

图6 传统遗传算法和改进多目标遗传算法的配送成本迭代过程Fig.6 Iterative process of distribution cost for traditional genetic algorithm and improved multi-objective genetic algorithm

为了进一步验证改进多目标遗传算法对于求解需求不确定和碳排放约束下农村物流配送路径优化问题的有效性和适用性,本研究经过20次仿真试验最终得出了需求覆盖率最大化、碳排放和配送成本最小化的最优配送方案和配送路径。改进多目标遗传算法下最优配送方案及成本构成见表5,改进多目标遗传算法下最优配送路径见图7。

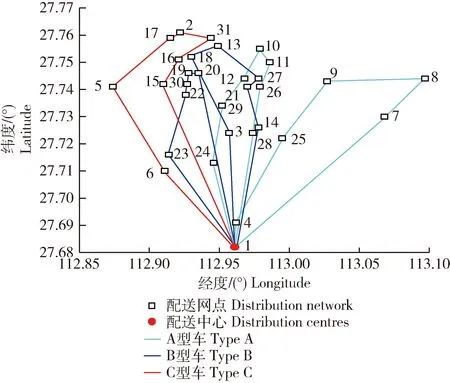
图7 改进多目标遗传算法下的最优配送路径Fig.7 Optimal distribution route under improved multi-objective genetic algorithm

表5 改进多目标遗传算法下最优配送方案及成本构成

5 结论与对策建议

针对需求不确定和碳排放约束的农村物流配送路径优化问题,本研究以需求覆盖率最大化、碳排放和配送成本最小化为目标构建了包含碳排放成本、固定成本、距离成本以及时间惩罚成本的农村物流配送路径优化模型,并设计了适用于多车型的改进多目标遗传算法对模型进行求解。仿真试验结果表明:1)与传统遗传算法相比,设计的改进多目标遗传算法对于求解需求不确定和碳排放约束的农村低碳物流配送路径优化问题具有更好的适用性和收敛性,其需求覆盖率、碳排放量和配送成本也优于传统遗传算法。2)满足客户需求和降低碳排放并不冲突,基于改进多目标遗传算法对农村物流配送路径进行优化求解,所得路径优化方案能有效提升农村物流需求覆盖率和降低物流碳排放。3)相对于单车型的配送方案而言,多车型的配送方案对于同时考虑需求不确定和碳排放约束的农村物流配送具有明显的优势。

基于以上研究结论,本研究提出以下4个方面的对策建议:1)完善农村物流基础设施,加快农村地区道路、仓储设施、配送中心等物流基础设施的建设步伐,打通农村物流末端配送“最后一公里”,进而提升农村物流的运作效率和需求覆盖率。2)科学合理布局农村物流网点,物流网点的设置要充分考虑用户需求量、配送距离、区域人流量等因素,积极寻求降低物流运作成本与提升物流需求覆盖率以及降低物流碳排放之间的平衡。3)大力推进共同配送模式在农村物流的应用,积极引导农村物流企业之间加强资源共享、信息互通和人员交流等,提升农村物流发展质量。4)完善农村物流碳排放监督机制,加快多车型新能源配送车辆的推广应用,从而降低农村物流的碳排放规模,促进农村物流的绿色健康发展。

另外,在未来的研究中将进一步研究地形和气候因素对我国农村物流配送路径优化的影响,针对不同地区的地形和气候条件分别构建更加完善的农村物流配送路径优化方案,为增强农村物流企业配送效率提供决策参考。