分布式阵列误差影响分析及估计方法

古 瑶,佘彩云,吴建新,胡刘博

(1.中山大学电子与通信工程学院,广东 深圳 518107;2.上海无线电设备研究所,上海 201109)

0 引言

分布式阵列雷达(distributed array radar,DAR)是下一代雷达发展的技术方向。相比于集中式阵列雷达,分布式阵列雷达具有波束分辨性能更好、抗干扰能力更强、探测效能更高、作战方式更灵活等优点[1]。由于分布式阵列雷达中各节点雷达均独立,各节点雷达的本振和通道的不一致性,以及各节点雷达间的时钟误差都会带来系统误差[2],各节点雷达参考阵元之间的位置误差[3]也会影响相参性能。

现有的阵列误差估计校正方法适用于分布式阵列雷达中各节点雷达共用频综和波控的情况,对于节点雷达独立、构成方式灵活的分布式阵列雷达则不适用。基于参数估计的阵列误差校正方法通过对误差建模,将其转化为参数估计问题,该方法可以对任意构型的阵列误差进行处理。根据校正源的应用情况,校正方法通常分为两大类:有源校正[4-5]和自校正[6]。

有源校正需要在空间设置特定的校正源,依靠校正源构造模型并求解。通过校正源的设置,能够在一定程度上增加信息量,从而降低运算量。自校正是一种基于某种优化函数对空间信源的方位与阵列的扰动参数进行联合估计的校正方法。其优点是不需要辅助校正源,可实时在线完成方位估计及误差校正,应用方便且具有较高的校正精度。上述方法虽然针对分布式阵列雷达提出了时间和相位的同步方案,但是没有考虑由位置误差引起的相位差,因此无法实现对位置误差的估计。由于平台运动,位置误差会随着时间的变化而改变,因此需要每隔一段时间进行一次在线估计,否则基线误差补偿的不准确会导致相位同步误差,进而使分布式阵列雷达的相参性能下降。

本文建立分布式阵列雷达误差模型,在此基础上讨论误差对相参处理的影响,并提出一种基于相位拟合的线性近似最小二乘误差估计方法。

1 信号模型

1.1 分布式阵列雷达信号模型

分布式阵列节点雷达沿x轴放置,以节点雷达1作为参考节点雷达,如图1所示。其中d1,2,分别为节点雷达1和节点雷达2参考阵元间的真实距离和含有误差的距离。

假定分布式阵列雷达系统由N部收发共置的相同节点雷达组成,每个节点雷达包含M个阵元,节点雷达内相邻阵元之间的距离de=λ/2,其中λ为发射信号的载波波长,相邻节点雷达之间的距离矩阵ddis= [d1,2d2,3…d(i-1),i…d(N-1),N],d(i-1),i为第i个节点雷达参考阵元与第i-1个节点雷达参考阵元间的真实距离,其中i∈{2,3,…,N}。该分布式阵列雷达的阵列导向矢量

式中:f0为雷达载频的中心频率;τi,j表示第i个节点雷达的第j个阵元相较于系统参考阵元的回波到达时间差,其中i∈{1,2,…,N},j∈{1,2,…,M}。

假定分布式阵列雷达中节点雷达1的阵元1为分布式阵列雷达的系统参考阵元,τi,j可以表示为

式中:τi,1为第i个节点雷达参考阵元与系统参考阵元的时间差;τ1,j为第1个节点雷达内第j个阵元与当前节点雷达的参考阵元间的时间差。可以看到,在远场条件下,分布式阵列雷达由于阵元间距导致的波程差可以分为阵内波程差和阵间波程差,因此阵列导向矢量sdis也可以表示为

式中:sa为阵间导向矢量;se为阵内导向矢量;⊗为Kronecker积运算符。

1.2 含误差的信号模型

基于前述的阵内和阵间导向矢量模型,对分布式阵列误差,包括阵内误差和阵间误差,分别进行讨论。对于第i个节点雷达内的第j个阵元,假定存在阵内时间同步误差和相位同步误差,同时存在通道增益不一致误差(偏离单位增益的倍数)gi,j、通道相位不一致误差及阵面姿态角误差。包含上述误差的第i个节点雷达的阵内导向矢量可以表示为

式中:θ为目标回波入射角。

假定阵间第i个阵元的时间同步误差为,相位同步误差为,通道增益不一致误差为gi,通道相位不一致误差为,由位置误差导致的波程差误差为。包含前述误差的阵间导向矢量可以表示为

式中:da为各节点雷达之间的距离。

假定目标的空间位置矢量pt=[xtyt]T(T表示矩阵转置),第i个节点雷达的第j个阵元的空间位置矢量pi,j=[xi,jyi,j]T,则τi,j可以写成

式中:‖·‖ 为范数运算符;c为光速。

假定θi表示第i个节点雷达的姿态角,其阵面姿态角误差为,相邻节点雷达阵间基线误差矩阵,其中为第i个节点雷达参考阵元与第i-1个节点雷达参考阵元间含有误差的距离,i∈{2,3,…,N}。无误差时,假定节点雷达阵列的阵内间距相等,选择阵元1作为当前节点雷达的参考阵元,参考阵元的位置矢量为pref,i,则第i个节点雷达的第j个阵元的位置矢量pi,j可以表示为

其中

式中:F（θi）为第i个节点雷达阵面姿态角对位置的影响矩阵。

假定分布式阵列雷达系统的参考阵元位置矢量pref,0=[x0y0]T,则第i个节点雷达的参考阵元位置矢量pref,i可以表示为

这里假定分布式阵列雷达沿x轴线性布局。考虑误差的第i个节点雷达的第j个阵元的位置矢量

其中

式中:为考虑误差的第i个节点雷达的参考阵元位置矢量。

2 误差影响分析

误差会影响分布式阵列雷达方向图的分布。当各误差项服从随机分布时,分布式阵列雷达方向图各点的值因误差的随机分布也会具有一定的随机性。若有确定的误差分布模型,则可对其影响进行确定性描述;若没有确定的误差分布模型,则可通过5 000次蒙特卡罗实验对其分布特性进行统计分析。相参积累效率随增益误差的变化情况如图2所示。其中相参积累效率是指含误差时相参处理的信噪比增益和理论相参处理的信噪比增益的比值。由实验结果可知,增益误差对相参处理增益的影响较大,相参积累效率随着增益误差分布均方差的增大而变小。

图2 相参积累效率随增益误差变化情况

相参积累效率随相位误差变化情况如图3所示。可知:综合的相位误差波动范围在40°以内时,相参积累效率在90%以上;相位误差波动范围在30°以内时,相参积累效率在95%以上;当相位误差波动大于130°时,相参积累效率几乎不变,保持在40%左右。

图3 相参积累效率随相位误差变化情况

综上所述,增益误差和相位误差都会对相参积累效率造成影响。各项误差间是相互独立的,因此可以对各项误差影响的指标进行累加,计算最终的误差影响程度。各误差项对相参积累效率的影响如表1所示。

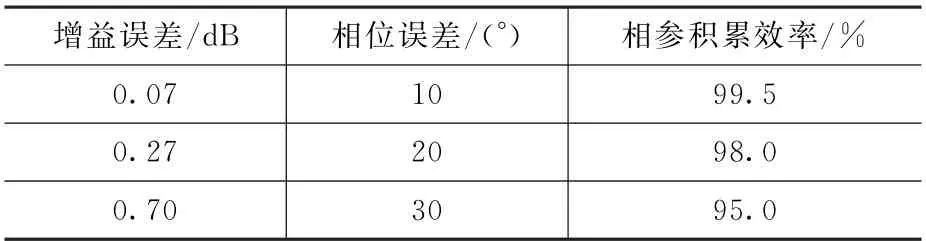
表1 各误差项对相参积累效率的影响

3 基于相位拟合的误差估计方法

3.1 迭代最小二乘误差估计

进行迭代最小二乘误差估计时,首先对节点阵列内的通道幅相误差进行校正,并估计由位置引起的相位误差及分布式节点间通道幅相不一致带来的误差。这些待估计的参数可以通过最小二乘估计获得,表达式为

式中:为估计的幅相误差矩阵;H 为共轭转置运算符。

将式(13)代入式(12)可以得到最小二乘代价式

式中:为估计的基线和姿态误差。

但上述最小二乘估计无法得到解析解,需要采用次优方法近似或者进行多维搜索。如果的求解只基于当前样本点,那么

将式(15)代入式(14),可得

式中:max(·)为取最大值函数;|·|为取绝对值运算符。

由于位置误差的存在,式(17)中观测导向矢量与理论导向矢量是失配的,因此使用理论导向矢量计算得到的是局部最优值。为了获得更准确的估计结果,可以迭代进行上述的最小二乘估计过程。基于迭代最小二乘的误差估计流程如图4所示。

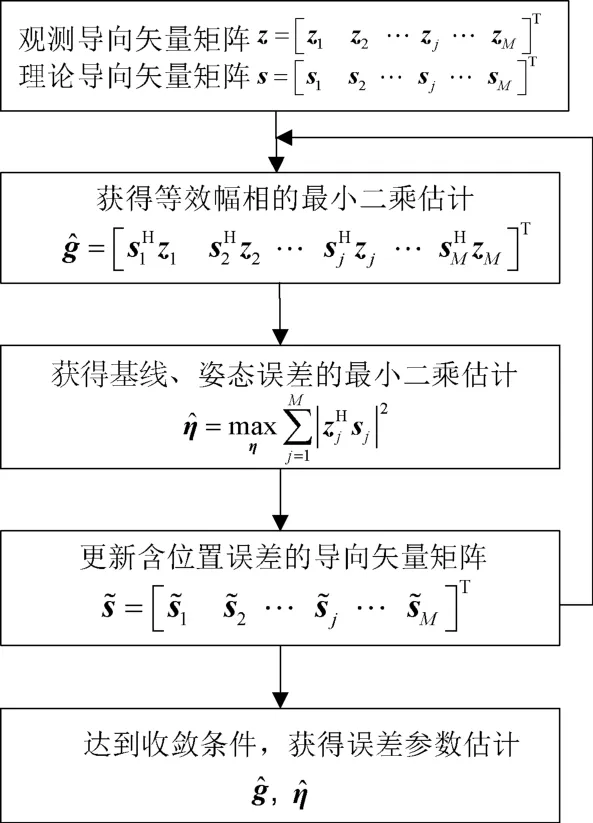
图4 基于迭代最小二乘的误差估计流程图

3.2 相位拟合的误差估计

由于采用的校正源信噪比较高,此时的数据相位可以认为是校正源的相位。通过提取输出相位进行参数拟合,就可以将非线性最小二乘问题进一步简化。

含误差的回波时延

其中

式中:为有误差时校正源到第i个节点雷达的第n行第l列阵元的距离;pt为校正源真实位置矢量;为有误差时第i个节点雷达的第n行第l列阵元的位置矢量;为有误差时第i个节点雷达参考阵元与第i-1个节点雷达参考阵元的距离;为有误差时第i个节点雷达的姿态角。

相对应的,含以上两种误差的第i个节点雷达的第n行第l列阵元的相位可以表示为

其中

式中:Δe为待估计的误差参数矩阵;为含误差的校正源m到第i个节点雷达的第n行第l列阵元的回波时延;φi为未校正的阵间通道相位;表示向下取整运算。

对式(19)所示距离表达式进行线性近似。首先处理姿态误差的非线性问题,将其在θi处进行泰勒(Taylor)展开,忽略2次以上的展开项,即

其中

由基线和姿态误差引起的位置误差矢量

令无误差时校正源到节点i的第n行第l列阵元的位置矩阵

结合式(24)和式(25),式(19)可改写为

式中:为无误差时校正源到第i个节点雷达的第n行第l列阵元的距离,通常也称为标称距离;分别为在x轴和y轴的坐标;为含有基线和姿态误差情况下校正源到第i个节点雷达的参考阵元的位置误差;为校正源到第i个节点雷达的阵面姿态角误差。

将式(20)写成矩阵形式,有

其中

式中:δ为第i个节点雷达的观测数据相位矢量;ei为位置误差矢量;Fi为距离标称矩阵;fi为相位列矢量;,分别为第i个节点雷达参考阵元在x轴和y轴的位置误差。

基于相位拟合的线性近似最小二乘误差参数估计流程如图5所示。

图5 基于相位拟合的线性相位最小二乘误差估计流程图

4 仿真实验

首先对线性近似相位与理论相位进行比较。在基线误差均方根误差为1 m、姿态角误差均方根误差为1°的情况下,线性近似相位相对于理论相位的误差如图6所示。

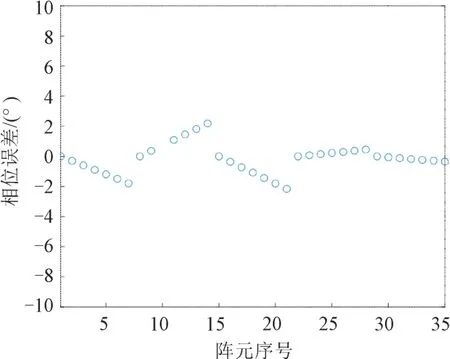
图6 线性近似相位相对于理论相位的误差

在获得位置误差后,可以对等效幅相误差进行估计。由于近似时相位存在近似误差,因此使用位置误差估计值代入式(19),计算得到的相位与理论相位存在偏差。经过500次蒙特卡罗仿真实验,在存在相位误差的情况下,分布式阵列位置误差修正后的通道间幅相估计平均误差如图7所示。从图7(a)可以看出,通道幅度增益平均相对误差随数据相位误差的增大而增大,当数据相位误差为3°时,通道幅度增益平均相对误差约为0.1。由图7(b)可知,数据相位误差不大于3°时,通道相位平均误差小于1.5°,近似带来的误差对通道增益的影响很小。使用估计的通道幅相误差进行校正均衡后,相参增益影响是可以接受的。

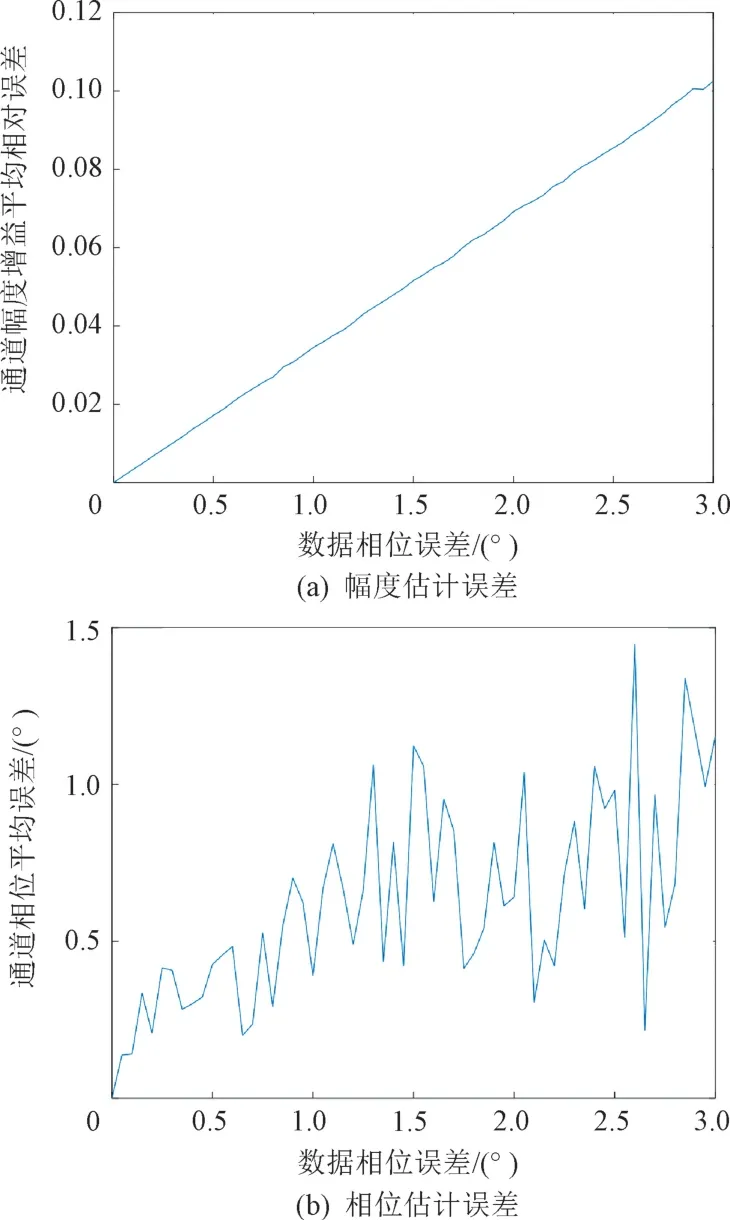
图7 位置误差估计修正后的通道间幅相估计平均误差

5 结束语

本文针对分布式阵列雷达系统中导向矢量非理想的误差问题进行研究。由于阵间误差难以进行完全的估计补偿,因此首先分析了阵间幅相误差对相参处理增益的影响,给出了不同性能指标下对误差剩余的要求,为误差估计校正方法的有效性提供支撑。之后对分布式阵列雷达的阵间位置和幅相误差进行估计,基于相位拟合和线性近似,完成对阵间误差的联合估计。通过对不同阵间相位误差剩余情况下的位置误差估计精度进行仿真,验证了该方法对误差估计的有效性。