基于脉冲控制的航天器顺光抵近与顺光构型维持

陆鹏飞, 王 悦*, 石 恒, 汤 亮

1. 北京航空航天大学宇航学院, 北京 102206 2. 北京控制工程研究所, 北京 100094 3. 空间智能控制技术全国重点实验室, 北京 100094

0 引 言

近地轨道上空间碎片的日益积累对航天器的发射与在轨运行造成了诸多潜在威胁,因此针对空间碎片减缓方面开展研究具有迫切的现实意义[1].现有的空间碎片减缓方法主要包括3个方面:被动减缓[2-3]、主动规避[4-5]和主动清除[6-8].其中主动清除指发射航天器接近并捕获目标碎片使其离轨再入,是一种能够高效减少空间碎片数量的方法.抵近技术是碎片主动清除任务设计中的关键技术,是实现进一步成像、捕获等在轨操作的前提.因此,有必要对抵近过程的轨道控制方法进行深入研究.顺光抵近指航天器沿着目标逆光方向,即近似位于目标和太阳连线之间对目标实施抵近操作.在实际工程中,顺光抵近具有非常重要的应用价值,可以为抵近航天器观测目标提供良好的光照条件,并在一定意义上降低抵近航天器的可观测性.

现有直接关于抵近轨道控制的研究较少,但在航天器交会轨道控制方面国内外已经积累了较多工作.在远距离交会方面,现有研究主要基于二体或受摄二体动力学模型展开研究,并且设计目标集中于降低完成交会所需的燃料消耗.根据推力方式的不同,存在脉冲变轨控制和小推力变轨控制两种方式.脉冲变轨为当前工程实际中使用最广泛的轨道控制方式,其中一种设计思路在LAWDEN[9]提出的主矢量理论基础上进行.该理论可以给出最优脉冲控制满足的必要条件,并为脉冲方式的改良提供指导,可用于设计脉冲变轨交会问题的控制策略[10-11].然而,该理论给出的最优性条件并不是充分的,并且数学推导较为繁杂.另一种方法是将脉冲交会问题建模为一个非线性规划(NLP)问题,通过数值优化算法进行求解[12-14].该类方法的难点在于描述最优变轨策略的NLP问题包含很多局部极值,需要采用一些启发式优化算法去获得全局最优解.另一方面,电推进方式具有更高的比冲,因此连续小推力变轨具有良好的应用前景.基于小推力变轨的交会问题可归结为一个最优控制问题,通过形状函数法[15]、直接法[16]、间接法[17]等途径可以设计满足最优性的推力控制.

远距离导引至目标附近后,航天器与目标间的近距离轨迹规划与控制通常在相对动力学下进行.常用的模型包括C-W方程、T-H方程、相对轨道要素法等.C-W方程适用于目标轨道为近圆轨道且相对距离较近的情况,T-H方程则将适用范围拓展至目标轨道偏心率较大的情形,相对轨道要素法可以用于相对距离更大的场景.在这些相对运动模型的基础上,一些近距离操作任务的规划与控制问题被进一步研究.文献[18]提出一种基于采样的近距离轨迹规划方法,可以实时解算燃料最优的相对运动.文献[19]中根据相对轨道要素法设计了水滴型悬停构型脉冲控制策略.文献[20]设计了对翻滚非合作目标的近距离抵近绕飞连续推力控制策略.文献[21]提出一种综合多步优化和序列二次规划的优化算法,用于求解远程抵近和近距离掠飞观测的最优轨迹.

然而,目前几乎还没有关于顺光抵近控制方法的研究见诸公开报道.本文对航天器近距离顺光抵近和顺光构型维持的脉冲控制策略设计进行研究.在目标轨道系下建立航天器对目标的近距离相对运动方程;研究了顺光抵近过程的脉冲控制问题,建立顺光走廊的几何概念,通过将路径约束转化为点约束的技巧,构建并求解描述最优脉冲变轨方式的NLP问题.进一步分析了目标轨道坐标系下的目标—太阳连线长期变化规律,并基于控制时刻与控制位置点采样以及动力学拟合的思路,设计了一种顺光位置维持的控制策略.通过数值算例验证了所提出控制策略的有效性.

1 相对运动动力学模型

本文研究对近圆轨道目标的顺光抵近问题.动力学模型为地球为中心的二体问题,抵近航天器与目标均假设为质点.以目标为原点,建立目标轨道坐标系,其中z轴指向地心,x轴在轨道平面内垂直于z轴,指向与目标平运动方向一致,y轴由右手定则确定,如图1所示,图中IJK为地球赤道惯性坐标系,O代表目标,SC代表抵近航天器,Δr为目标指向航天器的位置矢量.

图1 近距离相对运动示意图Fig.1 Schematic diagram of close-proximity relative motion

抵近航天器相对目标的运动可用C-W方程描述,表述为

(1)

式中,ω为目标的轨道平均角速率,x、y和z为Δr在目标轨道系O-xyz下的分量,fx、fy和fz为施加在航天器上的控制加速度.

(2)

式中,A和B为定常矩阵,其表达可参考文献[22].方程(2)的状态转移矩阵形式的解为

(3)

式中,t0为初始时刻,X0为状态变量在初始时刻的值,Φ(t,t0)为状态转移矩阵,其表达式为

(4)

式中,υ=ω(t-t0),s为sinυ,c为cosυ.

当抵近航天器以脉冲方式变轨时,式(3)变为

(5)

式中,ti是脉冲变轨的时刻,N为时刻t之前机动发生的次数,Δvi为抵近航天器对应ti时刻的脉冲速度增量矢量.

2 近距离顺光抵近脉冲控制策略

2.1 顺光走廊定义

本节从几何上给出顺光走廊的定义.由于抵近任务持续时长相比于地球绕太阳公转周期为小量,因此,假设任务过程中太阳在惯性空间中的方位不变,记太阳在地球赤道惯性系中的位置为rS,在计算中根据星历获取.设在时刻t目标的位置为rT(t),则该时刻由目标指向太阳的位置矢量为

L(t)=rS-rT(t)

(6)

顺光走廊定义为以目标为顶点、以目标—太阳连线为轴线的圆锥内的位置集合,示意图如图2所示,数学上可表达为

图2 顺光走廊定义Fig.2 Definition of the sunlight corridor

(7)

式中,θlim为圆锥的半锥角,称作走廊角.

由于在相对运动框架下设计近距离抵近控制,因此,为方便起见将顺光走廊转换到目标轨道坐标系中描述为

(8)

式中,rO和LO(t)分别为目标轨道坐标系下描述的相对位置以及目标—太阳连线方向,时刻t从地球赤道惯性坐标系向目标轨道坐标系的转换矩阵为式(9)所示.

(9)

其中,iT和ΩT分别为目标轨道的倾角和升交点赤经,而uT是t时刻目标的纬度辐角.

在目标轨道系中,太阳的方位时刻都在变化.因此,顺光走廊的定义依赖于时间.随着时间推移,在目标轨道系中,顺光走廊绕目标作定点转动.

2.2 抵近初始状态建立

抵近航天器在初始时刻t0可能位于顺光走廊外,为了保证后续抵近任务的顺利开展,需要建立合适的抵近初始状态.

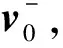
X-(tini)=Φ(tini,t0)X+(t0)

(10)

式中,“-”表示脉冲前,而“+”表示脉冲后.将状态量拆分为相对位置与相对速度的分块形式

(11)

(12)

(13)

2.3 顺光抵近控制脉冲优化

建立抵近初始状态后,通过多脉冲变轨的方式,控制抵近航天器的相对轨迹位于动态变化的顺光走廊内,实现从距离目标dini处抵近至距离目标dfin处,并要求在给定时间上限Δtlim内完成.最优的脉冲控制策略通过NLP问题的构建与求解确定.

NLP问题的优化变量包括N次脉冲机动的时刻,及其幅值、方位角和仰角,记作

w=(t1,…,tN,Δv1,…,ΔvN,α1,…,αN,β1,…,βN)

其中,ti、Δvi、αi和βi分别为第i次脉冲的时刻、幅值、方位角和仰角,i=1,…,N.方位角和仰角在目标轨道坐标系中定义,其中方位角αi指速度增量矢量在xy平面上的投影与x轴间的夹角,仰角βi指速度增量矢量与xy平面的夹角.

期望控制过程中的脉冲代价最小,因此NLP问题的目标函数设计为N次脉冲机动幅值总和

(14)

顺光抵近过程考虑的约束包括3类,第一类为优化变量需满足的界约束,包括

(1)脉冲时刻的上下界约束

tini≤t1≤t2≤…≤tN≤tini+Δtlim

(2)单次脉冲速度增量幅值的上下界约束

0≤Δvi≤Δvlim,i=1,…,N

(3)脉冲方向角约束

0≤αi≤2π
-π/2≤βi≤π/2,i=1,…,N

第二类约束为终端相对位置和相对速度约束,表述为

(15)

式中,r(tN)和v(tN)可通过式(5)表述为优化变量的函数,分别为

(16)

推导中用到了常矩阵B的值,B=[03×3I3×3]T.

第三类约束表征在抵近过程中,抵近航天器的相对位置一直处于顺光走廊内,为一个路径约束

(17)

利用放缩技巧,将约束(17)转化为点约束

(18)

数值测试表明,式(18)中“[ ]”内关于t的函数极大值数量很少,可通过分区间求解极值的方法获得最大值.

综合前述分析,所构建的用于求解最优脉冲控制策略的NLP问题可以表述为如下形式:

(19)

对该NLP问题用粒子群优化(PSO)算法进行求解,可以得到实现顺光抵近操作最优的脉冲控制方式以及对应的轨迹.

3 顺光构型维持脉冲控制策略

本节介绍在顺光抵近过程结束后,实现抵近航天器位置维持在顺光走廊内且持续较长时间的脉冲控制策略.首先对目标—太阳连线方向在目标轨道坐标系中的长期变化规律进行分析,随后设计了一种基于控制时刻与控制位置点采样,以及轨迹动力学拟合的顺光构型维持策略.

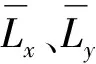
(20)

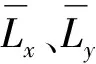
则式(20)中的第1式和第3式简化为

(21)

(22)

基于上述分析可知,若卫星与目标保持恒定距离并持续位于顺光走廊内,卫星相对目标的运动在目标轨道面法向分量近似保持恒定值,而在目标轨道面内的运动分量近似位于以目标为圆心的圆上,且变化周期与目标轨道周期相同.由于C-W方程形成的自然相对运动在目标轨道面法向上的分量为关于目标轨道面的振动,难以保持于顺光走廊内.因此,本节后续设计了一种基于控制时刻与控制位置点采样,以及轨迹动力学拟合的脉冲控制策略,以实现顺光构型的长时间维持.

由于研究中考虑对近圆轨道目标的抵近,目标的轨道角速率接近常值.因此,由式(22)可推断出,顺光走廊的定点转动角速率也近似为常值.所以将目标轨道周期T=2π/ω等间隔划分为M段,选取控制时刻节点

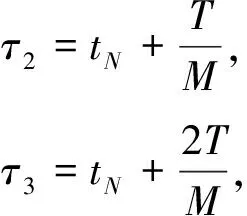
对于每一个控制时刻节点,解算对应时刻目标—太阳连线上距离目标dfin处点的相对位置矢量,作为控制位置点.

rn,1=dfin·LO(τ1),
rn,2=dfin·LO(τ2),
⋮
rn,M+1=dfin·LO(τM+1).

对相邻的两个控制时刻节点及对应的控制位置点进行相对Lambert问题的求解,以确定这段时间内抵近航天器满足两点边界位置约束和飞行时间约束的相对运动轨迹.本文中相对Lambert问题基于C-W方程的状态转移形式求解,其核心为根据某段相对轨迹的始末位置约束,计算其始末时刻速度,计算公式已由式(12)给出,不再赘述.以τi～τi+1段为例,在τi时刻,满足约束的相对速度为

(23)

在τi+1时刻,满足约束的相对速度为

(24)

类似可以解出在每一个控制时刻节点,分别满足前一段相对运动轨迹约束和后一段相对运动轨迹约束对应的相对速度,示意图如图3所示,在第i个时间节点,用于拟合轨迹的速度增量为

图3 相对轨迹动力学拟合Fig.3 Dynamical fitting of relative motion’s trajectories

(25)

tN+T时刻后的每一个周期内都可用上述方法设计维持的脉冲策略,从而实现长时间的顺光构型位置保持.

4 数值实例

通过两个算例来验证方法的有效性,第1个算例中目标运动在地球静止轨道(GEO)上,第2个算例中目标运动在太阳同步轨道(SSO)上.两个算例的初始时刻都为UTC时间2025年1月1日0时0分0秒.在初始时刻目标和抵近航天器的轨道六要素见表1.由DE438星历文件计算得到该时刻太阳在地球J2000坐标系中的位置矢量投影为[0.267 327 -1.327 243 -0.575 347]T×108km,顺光走廊的走廊角θlim取2.5°.基于第2和第3节中的方法分别设计抵近与构型维持控制策略.仿真动力学模型为考虑地球扁率J2项的受摄二体问题,其中地球引力常数取398 600.5 km3/s2,地球半径取6 371.11 km,J2项系数取1.082 63×10-3.

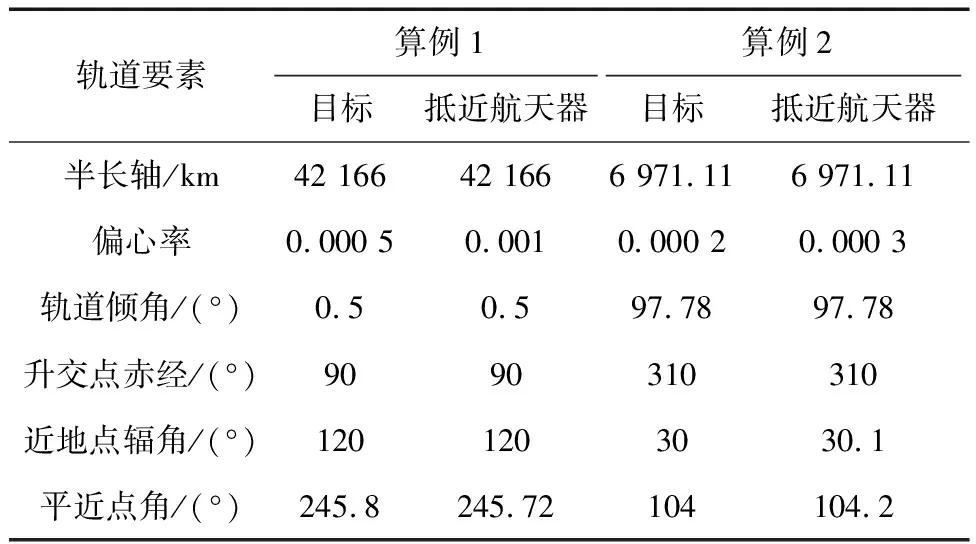
表1 初始轨道要素取值Tab.1 Values of the initial orbital elements

4.1 顺光抵近算例

算例1要求抵近航天器首先在4 h内建立抵近初始状态,然后从距离目标50 km处顺光抵近至距离目标10 km处,用时不超过2 h;算例2要求抵近航天器首先在0.5 h内建立抵近初始状态,然后从距离目标25 km处顺光抵近至距离目标10 km处,用时不超过2 h.首先基于2.2节中的方法建立抵近初始状态.算例1的计算结果为第一次变轨脉冲消耗6.82 m/s,第二次变轨脉冲消耗8.03 m/s,建立抵近初始状态总脉冲消耗14.85 m/s,图4为算例1建立抵近初始状态过程的相对运动轨迹,图5为该阶段目标与航天器间距离的变化.算例2的计算结果为第一次变轨脉冲消耗16.36 m/s,第二次变轨脉冲消耗10.35 m/s,建立抵近初始状态总脉冲消耗26.71 m/s.图6和图7分别展示了算例2这一阶段的相对轨迹以及目标与航天器间距离变化.从结果中可以看出,抵近航天器成功于给定时间转移至目标—太阳连线上距离目标给定距离的位置附近.

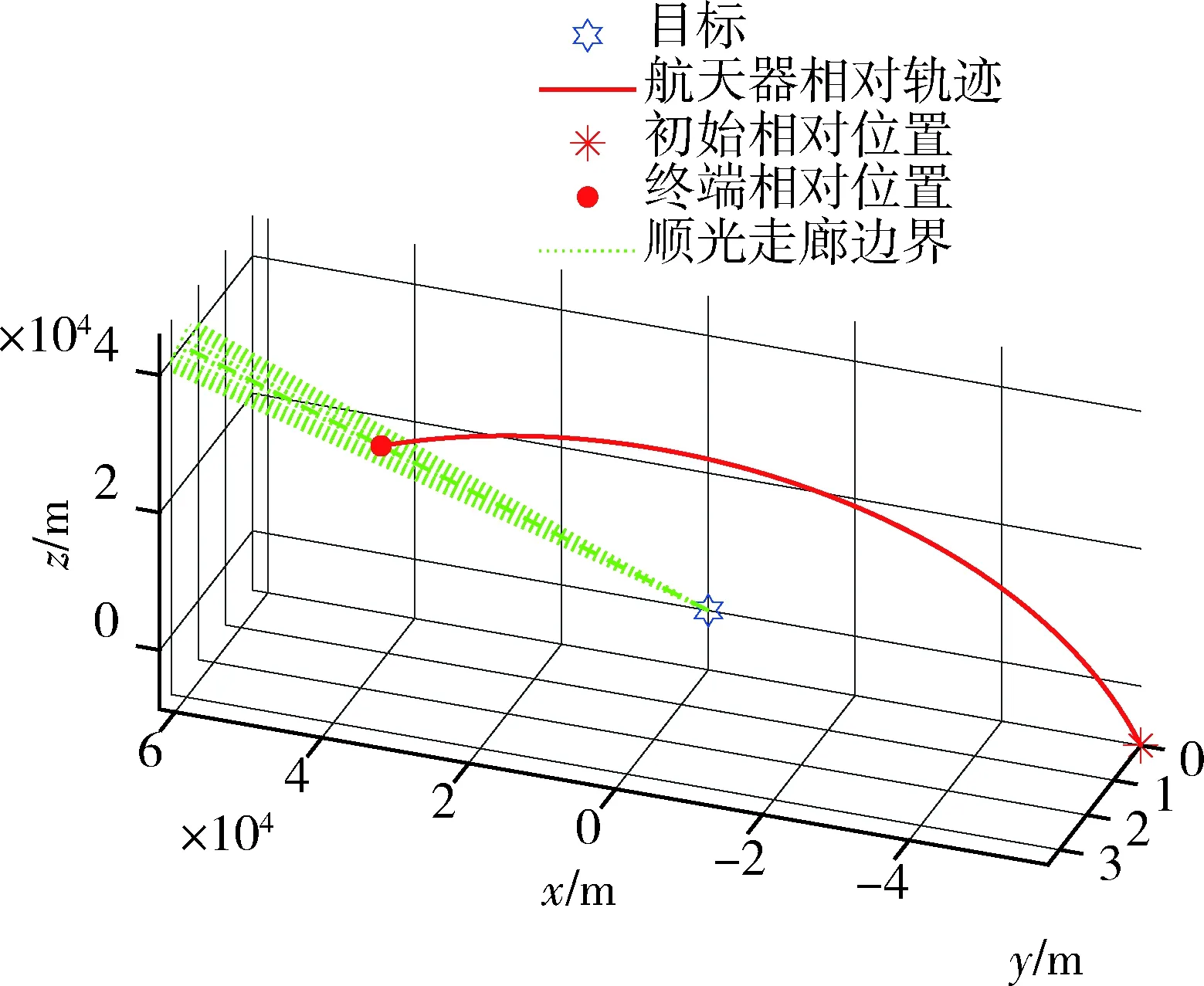
图4 建立抵近初始状态过程的相对运动轨迹(算例1)Fig.4 The relative motion during the establishment process of the initial state (case 1)

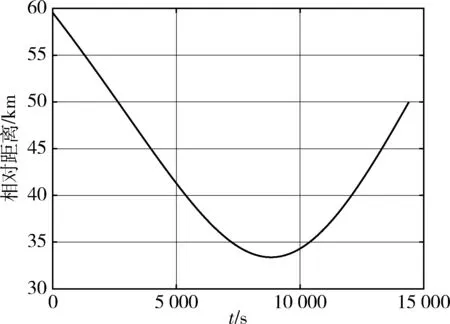
图5 建立抵近初始状态过程的相对距离(算例1)Fig.5 The distance between the target and the spacecraft during the establishment process of the initial state (case 1)

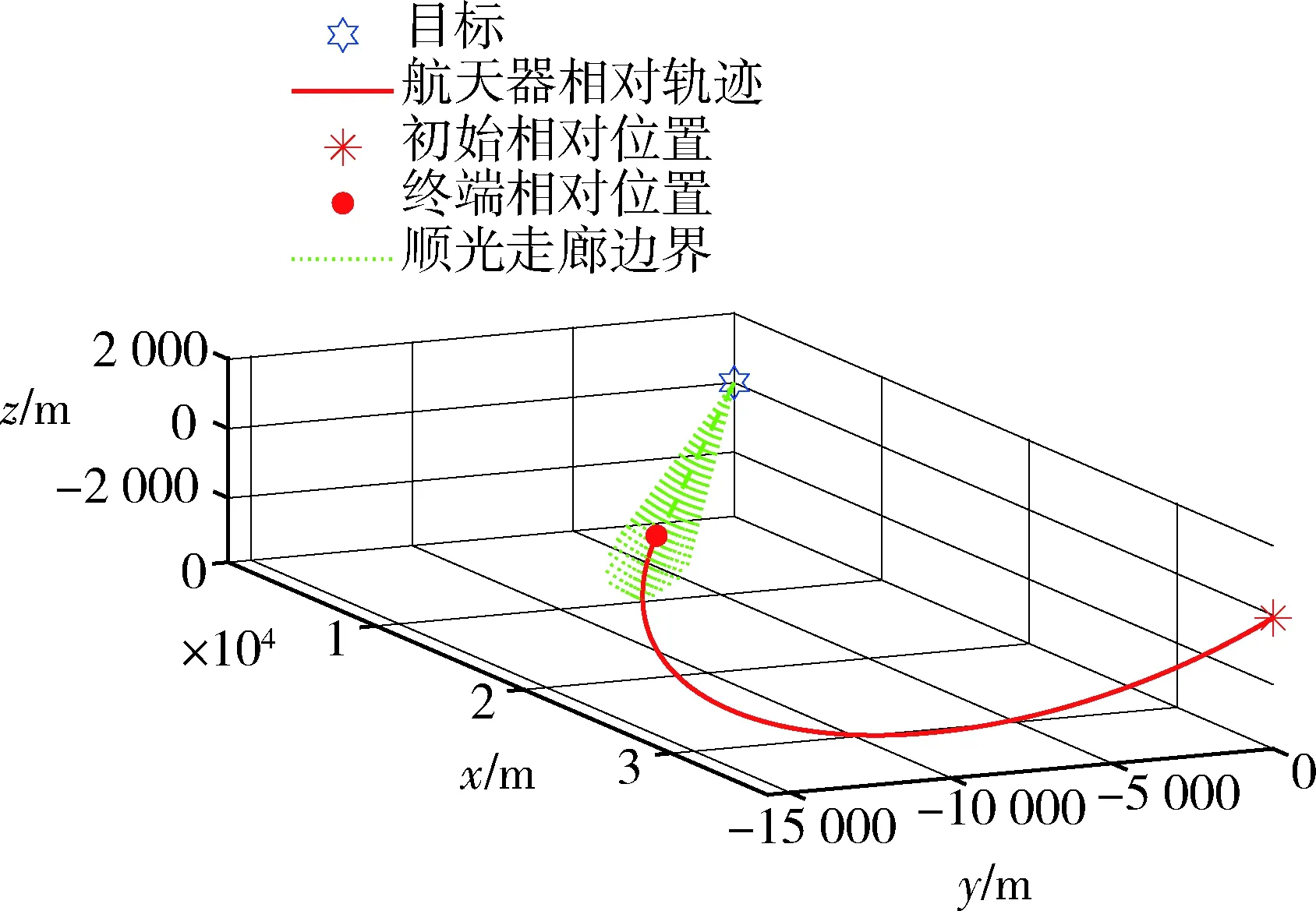
图6 建立抵近初始状态过程的相对运动轨迹(算例2)Fig.6 The relative motion during the establishment process of the initial state (case 2)

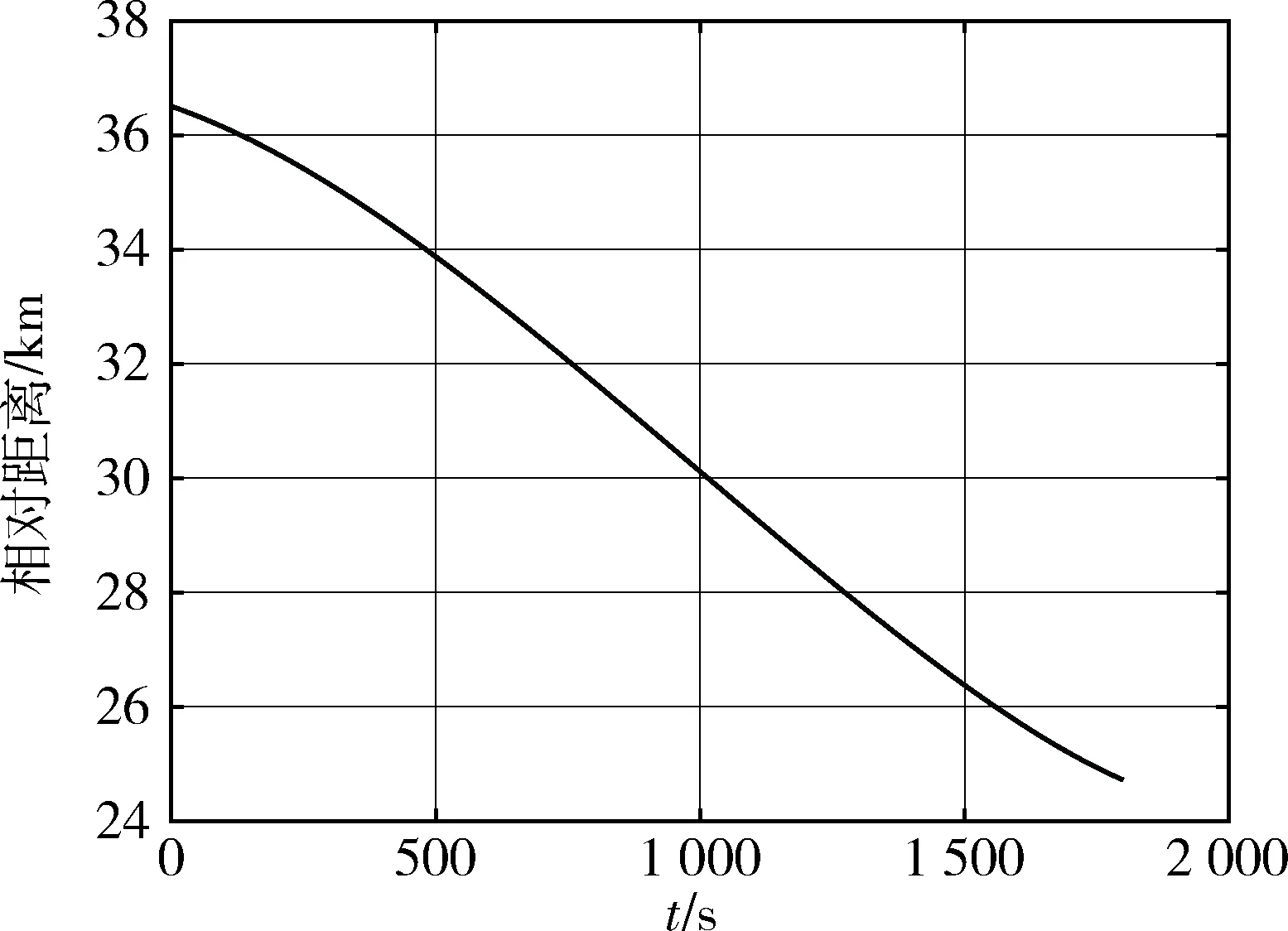
图7 建立抵近初始状态过程的相对距离(算例2)Fig.7 The distance between the target and the spacecraft during the establishment process of the initial state (case 2)

随后,基于2.3中的方法设计顺光抵近过程的控制脉冲及运动轨迹.在构建的NLP问题中,取脉冲次数上限为5,通过粒子群优化算法求解NLP问题,粒子个数取20,迭代次数为2 000.算例1所得最优的控制脉冲消耗量为12.56 m/s,抵近过程用时为2 h,优化出的实际脉冲策略退化为始末时刻各执行一次脉冲,其中第1次脉冲大小为6.66 m/s,第2次脉冲大小为5.90 m/s;算例2优化出的最小控制脉冲消耗量为51.51 m/s,抵近过程用时0.296 3 h,优化出的实际脉冲次数为3脉冲,大小分别为21.48 m/s、15.08 m/s和14.94 m/s.

算例1抵近过程的相对轨迹见图8.目标—航天器连线与目标—太阳连线夹角随时间变化的关系如图9所示,抵近过程目标与航天器间的距离如图10所示;算例2对应的结果见图11～13.从结果中可见,抵近过程中,航天器位置一直位于顺光走廊内,从较远距离顺利抵近至距目标10 km附近.由于仿真采用了更精确的模型,因此仿真结果与标称设计结果存在少量的偏差,但不影响结果对所设计控制策略的有效性证明.

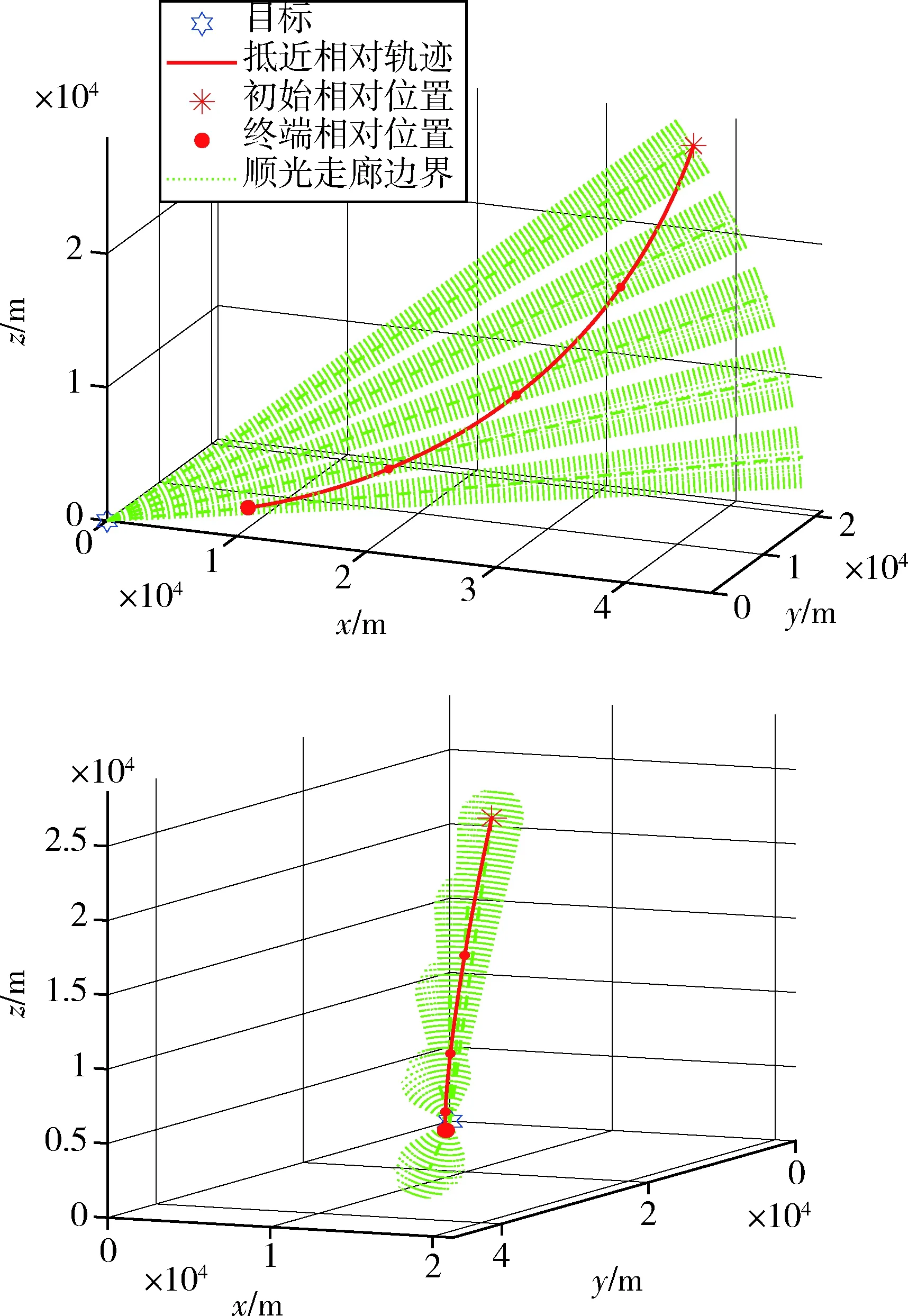
图8 抵近过程的相对运动轨迹仿真(算例1)Fig.8 The relative motion during the approach process (case 1)

图9 抵近过程目标—太阳与目标—航天器连线角偏差仿真结果 (算例1)Fig.9 The angular deviation between the line of target-Sun and that of target-spacecraft during the approach process (case 1)

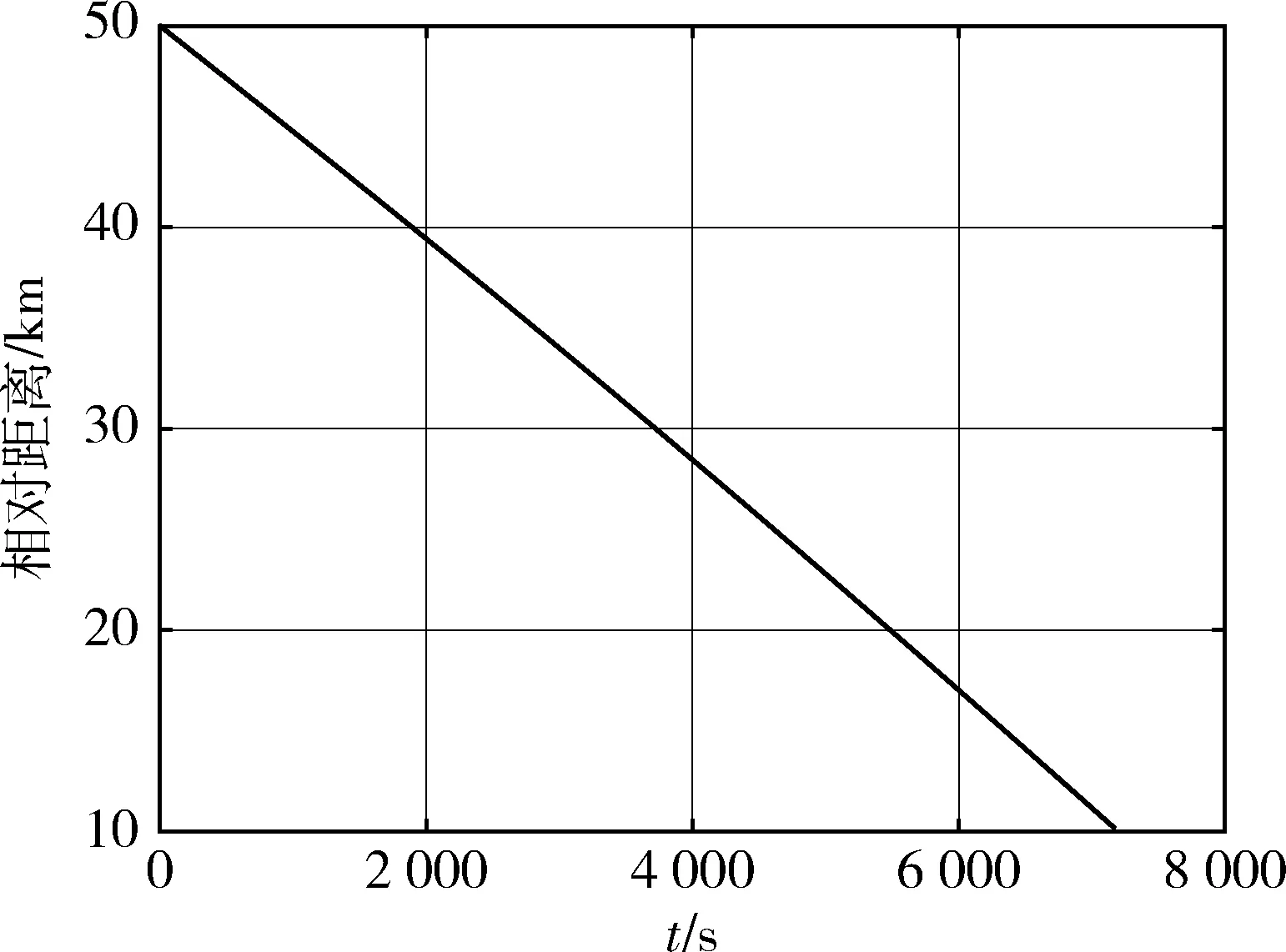
图10 抵近过程相对距离仿真结果 (算例1)Fig.10 The distance between the target and the spacecraft during the approach process (case 1)

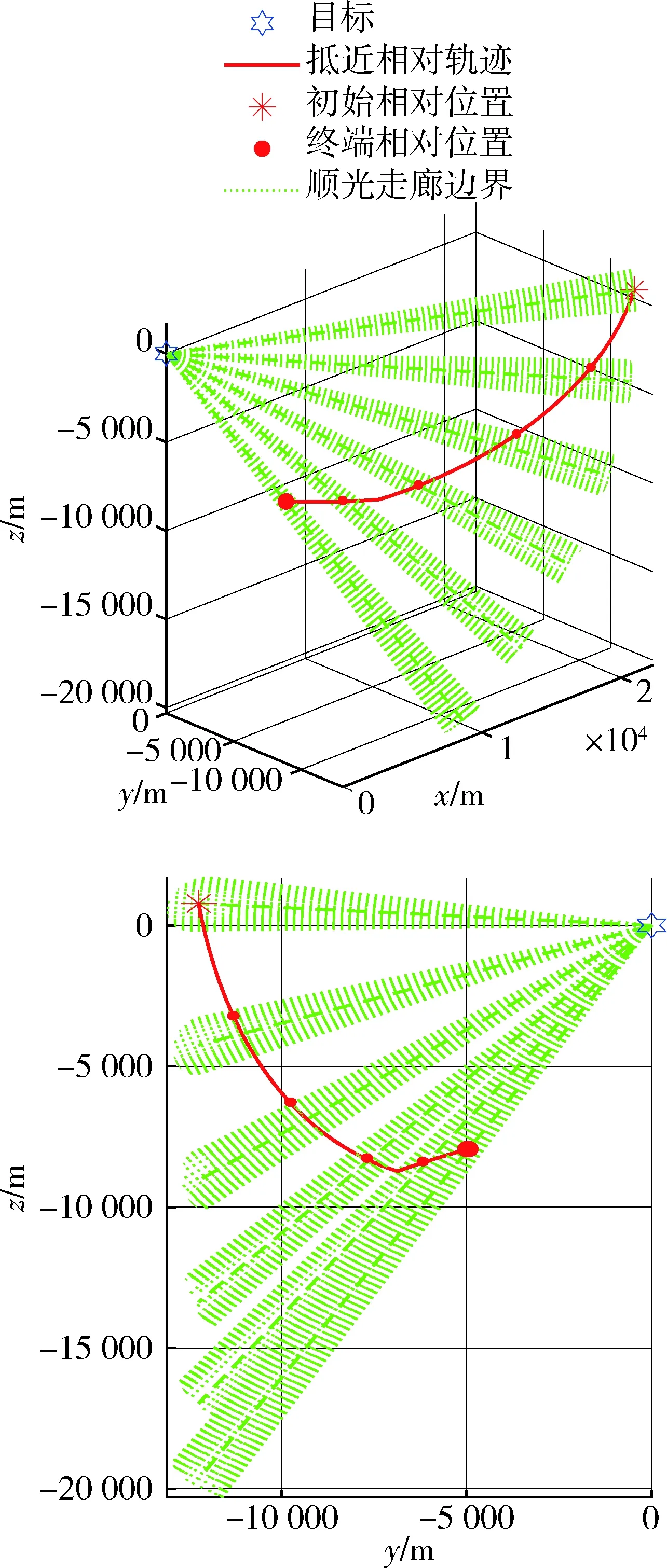
图11 抵近过程的相对运动轨迹仿真(算例 2)Fig.11 The relative motion during the approach process (case 2)

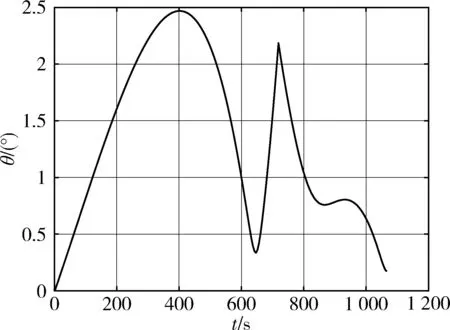
图12 抵近过程目标—太阳与目标—航天器连线角偏差仿真结果(算例 2)Fig.12 The angular deviation between the line of target-Sun and that of target-spacecraft during the approach process (case 2)

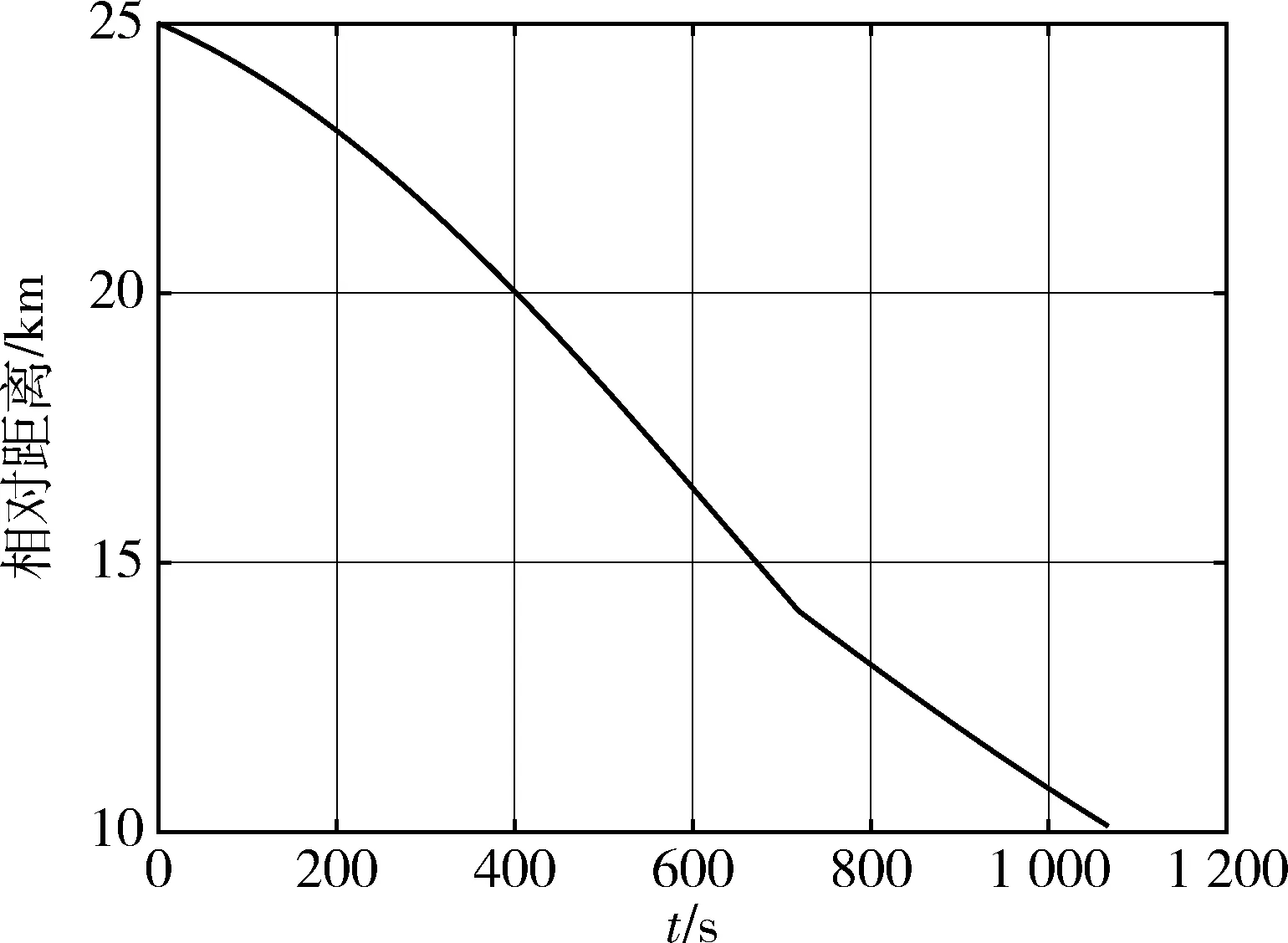
图13 抵近过程相对距离仿真结果(算例2)Fig.13 The distance between the target and the spacecraft during the approach process (case 2)

4.2 顺光构型维持算例

在4.1中算例的基础上,对完成顺光抵近后航天器在顺光区域内的位置维持进行设计.以维持一个目标轨道周期为例,即23.936 h.根据第3节中的算法实现,首先将期望维持时长等间隔划分为15个区间,选取16个控制时间节点,用相对Lambert问题进行动力学拟合.最终算例1中维持单个周期所需要的脉冲速度增量消耗共计6.33 m/s,平均每次控制脉冲大小为0.422 m/s;算例2中维持单个周期所需要的脉冲速度增量消耗共计93.30 m/s,平均每次控制脉冲大小为5.83 m/s.图14～16分别展示了算例1构型维持中航天器的相对轨迹、目标—航天器连线与目标—太阳连线夹角随时间变化的关系以及目标与航天器间的距离.图17～19展示算例2中的相关结果.根据结果可见,在考虑了J2项摄动的更高精度模型下,所设计的控制方法仍可以实现目标—太阳与目标—航天器连线角偏差保持于较小范围内,在第1个算例中小于2°,在第2个算例中小于5°.因此,所提出的脉冲控制策略能够完成航天器在目标顺光走廊内的长时间维持任务.

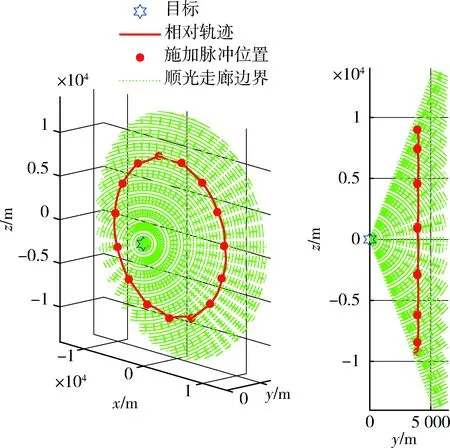
图14 维持过程的相对运动轨迹(算例1)Fig.14 The relative motion during the maintenance process (case 1)

图15 目标—太阳与目标—航天器连线角偏差(算例1)Fig.15 The angular deviation between the line of target-Sun and that of target-spacecraft during the maintenance process (case 1)

图16 维持过程相对距离 (算例1)Fig.16 The distance between the target and the spacecraft during the maintenance process (case 1)

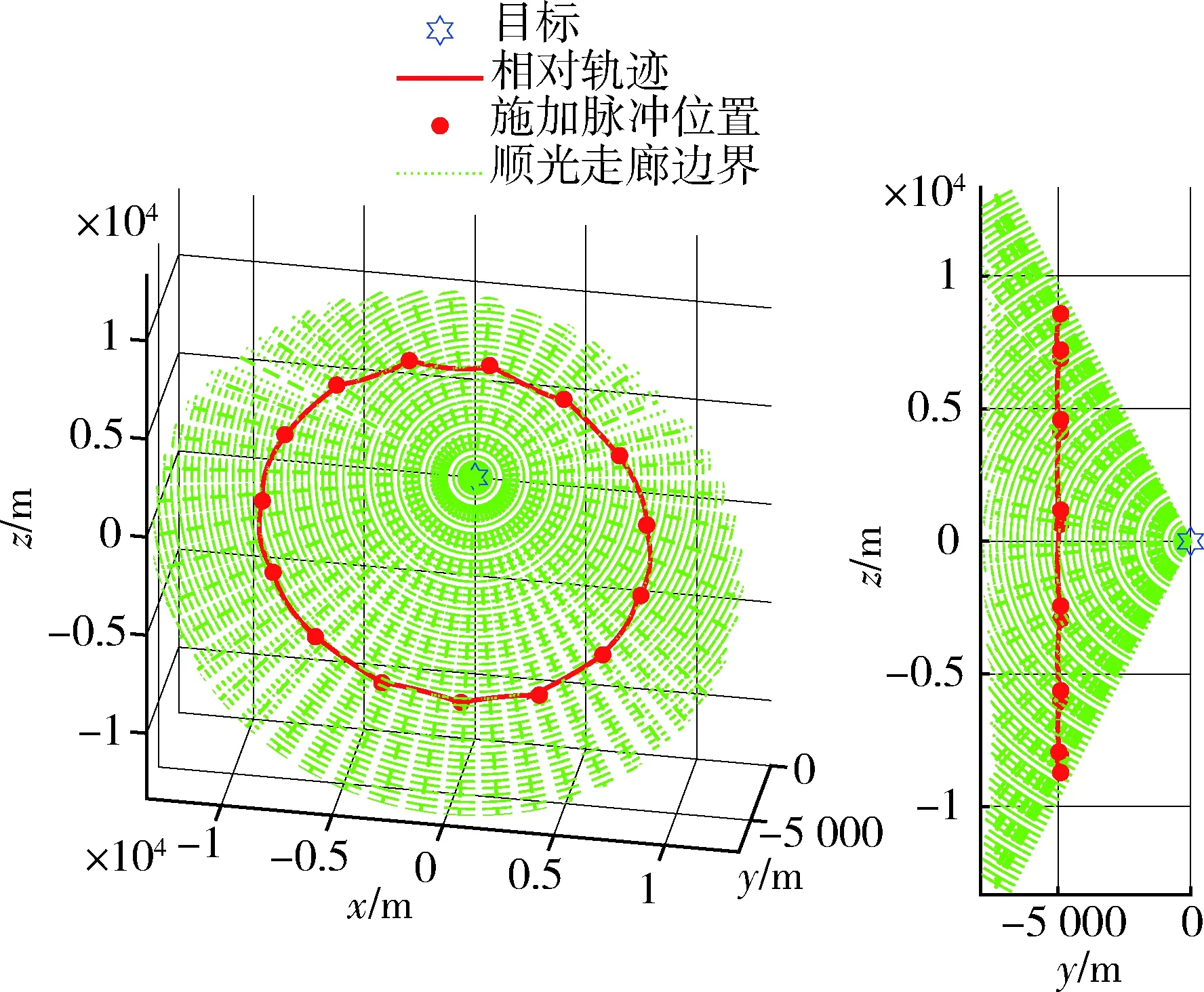
图17 维持过程的相对运动轨迹(算例2)Fig.17 The relative motion during the maintenance process (case 2)

图19 维持过程相对距离 (算例2)Fig.19 The distance between the target and the spacecraft during the maintenance process (case 2)

表2 维持效果与维持消耗结果 (算例1)Tab.2 Results of the performance and cost for maintenance (case 1)

下面进一步分析控制节点数目对维持精度与维持消耗的影响.取控制节点数分别为9、12、16和21,进行一个目标轨道周期时长的顺光构型维持,算例1与算例2对应的维持效果与维持消耗分别在表2和表3中给出.分析结果可知,一般来说,控制节点数越多,则维持过程中的最大角偏差与距离偏差越小,且脉冲消耗没有显著增加.实际使用中可根据控制误差需求合理设置控制节点数.但在算例2中当控制节点增加到一定数目时,无法通过继续增加节点的数目来降低角偏差,其原因是因为该算例中目标轨道高度较低,地球J2项摄动较为显著,偏差的主要来源已经变成了设计模型与仿真模型间的偏差.未来可以进一步研究考虑各种摄动情况下的顺光抵近与顺光构型维持控制策略.

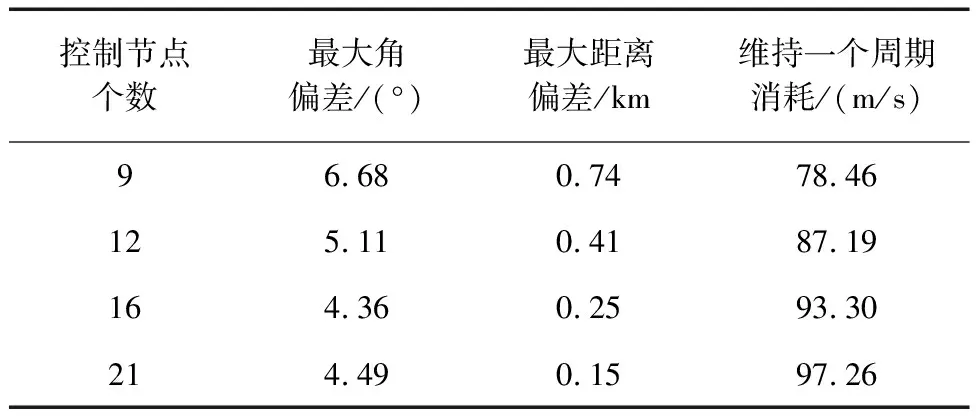
表3 维持效果与维持消耗结果 (算例2)Tab.3 Results of the performance and cost for maintenance (case 2)

5 结 论

本文研究了对空间目标近距离顺光抵近与顺光构型维持的脉冲控制问题.建立顺光走廊的几何概念,提出一种基于NLP模型的顺光抵近最优脉冲控制策略求解方法.分析目标轨道坐标系下的目标—太阳连线长期变化规律,设计基于控制时刻与控制位置点采样和动力学拟合的顺光构型维持策略,并进行数值实例求解与分析.仿真结果表明,所提出的方法可以有效地完成顺光抵近任务与顺光构型维持任务,具备良好的实用性能.