失效航天器等离子羽流消旋建模与最优制导研究

代洪华, 左宸昊*, 赵弘骞, 商崇余

1. 西北工业大学航天学院, 西安 710072 2. 航天飞行动力学技术国家级重点实验室, 西安 710072

0 引 言

近年来,随着各国太空活动次数逐渐增加,人造航天器的数量急剧增多.但同时,空间中的失效航天器、航天任务产生的抛弃物以及碰撞产生的航天器碎片等大量空间垃圾对人类后续的航天事业发展构成了巨大威胁[1].截至2023年4月,太空中现存的航天器数目已突破11000个,其中正常运行的航天器约7800个,失效航天器占比高达29%,失效航天器占据了大量宝贵的轨道资源[2].凯斯勒现象表明,当失效航天器的数量达到一定程度时,将会严重阻碍航天器的发射和使用[3].

空间中的失效航天器大多为非合作目标且已经失去主动控制能力,在其失控前残余角动量的影响下长期处于自由翻滚状态,而太空中的各种摄动会使其运动状态更加复杂[4-6].为避免失效航天器的威胁,需要对其进行在轨操作[7],通过对失效卫星进行消旋,稳定其运动状态,能够极大地降低在轨操作任务的难度,保证任务安全进行.因此,消旋是失效航天器在轨操作的关键内容.

根据服务航天器对失效航天器施加阻尼的方式不同,可将消旋方法分为接触式消旋和非接触式消旋两类.其中接触式消旋如绳系机器人消旋、减速刷消旋等,是通过服务航天器的末端执行器直接接触施加消旋力,其消旋力指向性强、接触消旋力大[8],但是直接接触容易损伤失效航天器结构、同时近距离接触也存在碰撞风险[9].非接触式消旋如涡流消旋、等离子羽流消旋、气体羽流消旋等,是通过电磁场、羽流等介质间接产生消旋力矩,能够有效避免服务航天器与失效卫星之间的碰撞,在消旋过程中还可通过参数调节实现柔顺消旋.为克服传统分子羽流消旋燃料消耗大、粒子作用范围分散的难题,本文提出了一种利用霍尔效应推进器产生的等离子羽流进行消旋的方法.充分发挥霍尔推进器比冲高、高效率、快启动[10]与羽流作用范围集中的优势,实现低燃料消耗的安全灵活消旋.

在等离子羽流建模方面,VANGILDER等[11]将细胞粒子法和直接蒙特卡罗方法相结合来对霍尔推进器的羽流进行建模,并将流场计算结果与实验测量数据进行比较.CHEN[12]通过分析等离子羽流中的离子与原子的运动状态,基于麦克斯韦速度分布函数进行羽流建模.在空间操控方面,BOMBARDELLI等[13]提出了“离子牧羊人(IBS)”概念,他们结合目前离子推力器的技术水平,对等离子羽流清除空间碎片的能力进行了评估.ASLANOV等[14]在离子牧羊人项目的基础上研究了空间碎片在离子束及多种扰动作用下的运动情况.DAI等[15]首先提出等离子羽流消旋概念,建立了等离子羽流消旋模型.目前多数羽流建模方法需要复杂的数值积分运算,在服务航天器的星载计算环境下难以在轨实时应用,因此急需开发一种基于启发式算法的等离子羽流冲击力高效计算模型,为消旋操控奠定模型基础.

羽流操控的优化配置是提高消旋效率的关键技术,其核心是设计羽流指向的制导律,在保证服务航天器与目标之间不发生碰撞的基础上提高等离子羽流的消旋效率,目前该方面前人研究较少.刘育琦等[16]基于参数化羽流撞击模型,利用指数和余弦的函数特性建立的目标函数实现了羽流瞄准策略的优化设计.LIU等[17]通过在消旋的制导、导航与控制系统中添加安全约束以及一系列控制方法实现了涡流消旋系统的稳定控制[18-19].上述制导方法多数针对单轴转动进行消旋,以消旋力矩最大为目标设计制导算法.但失效航天器普遍存在自旋与章动耦合的复杂姿态运动,因此需要在单轴消旋制导律的基础上发展自旋章动耦合的消旋策略.

综上,本文针对等离子羽流模型的复杂性建立基于机器学习的消旋力矩快速计算模型,并针对失效航天器的自由翻滚状态设计自旋章动耦合消旋制导策略.其主要内容为通过改进传统等离子羽流模型建立数据库,使用神经网络建立等离子羽流消旋力矩快速计算模型,在保证计算精度的条件下极大地缩短消旋力矩的计算时间.基于快速计算模型提出等离子羽流指向制导律,重点解决自旋与章动的耦合消旋问题,提高复杂翻滚运动的消旋效率.

1 等离子羽流消旋动力学系统

1.1 系统描述

等离子羽流消旋系统由自由翻滚的失效航天器与带有机械臂以及霍尔推进器的服务航天器组成,消旋相对位置如图1所示.

图1 等离子羽流消旋示意图和坐标系定义Fig.1 Schematic diagram of plasma plume detumbling and definition of coordinate frames

坐标系定义如下:

(1)惯性坐标系:地心惯性坐标系可以表示为I={OI,XI,YI,ZI},其原点位于地心,XI从地心指向春分点,YI从地心指向北极,YI与XI,ZI根据右手定则构成笛卡尔坐标系;

(2)航天器体坐标系:目标本体坐标系和服务航天器本体坐标系分别表示为t={Ot,Xt,Yt,Zt}与c={Oc,Xc,Yc,Zc},坐标系原点位于航天器质心,坐标轴与惯性主轴平行;

(3)喷口坐标系:霍尔推进器喷口坐标系表示为n={On,Xn,Yn,Zn},坐标系原点位于喷口中心,Xn为喷口指向方向,Yn位于XtOtYt平面内,Zn与Xn,Zn根据右手定则一起构成笛卡尔坐标系.

1.2 失效卫星动力学模型

失效航天器的自由翻滚动力学方程可由欧拉动力学方程表示[20]

(1)

其中,上标t代表其在目标航天器本体坐标系表示.tI=diag{Ix,Iy,Iz}为目标的转动惯量,tω=[ωxωyωz]T是在目标航天器体坐标系下表示的角速度,tτ=[τxτyτz]T是失效卫星受到的等离子羽流消旋力矩.其中

(2)

失效航天器的运动学方程可由欧拉运动学方程表示

(3)

其中,σ=[φθψ]T为通过“3-1-2”旋转得到的目标欧拉姿态角.

1.3 等离子羽流消旋力矩模型

将霍尔推进器的环形喷口模型进行简化如图2所示.粒子在喷口处的速度分布满足麦克斯韦函数,则喷口处的粒子速度可以表示为[21]

图2 喷口简化示意图Fig.2 Simplified schematic diagram of nozzle

(4)

式中:ΔVj=(u-u0j)2+v2+w2,u、v和w分别为粒子在喷口坐标系三轴Xn、Yn和Zn方向上的速度分量,βj=1/(2kbT0j/mj),kb是波尔兹曼常数,mj是粒子的质量;n0j、u0j和T0j分别是第j种粒子在霍尔推进器出口处的初始粒子数密度,初始平均轴向速度和初始温度.从喷口坐标系内一点(x,y,z)出发的粒子到达空间内一点(X,Y,Z)处的初始速度应满足

(5)

当粒子从喷口平面(0,y,z)出发时,式(5)可表示为

(6)

式中,r为径向坐标,θ为出口截面内从Yn轴正方向转动得到的角度,如图2(a)所示.霍尔推进器为轴对称环形喷口,由此产生的羽流也是轴对称的,因此以Y=0为例计算一个径向方向的羽流模型,由此可以得到从喷口平面出发的粒子在空间内任意一点的速度为

(7)

式中,

(8)

根据式(6)～(8)的粒子速度表达式,通过积分转化就可以计算得到羽流在帆板表面产生的粒子数密度、粒子数通量和冲击压力等局部气体参数.考虑轴对称的影响,对CHEN的模型进行改进可以得到粒子在点(X,0,Z)处压强表达式为

(9)

(10)

帆板受到的由粒子漫反射产生的压强为

(11)

根据式(9)～(11)可以得到霍尔推进器产生的等离子羽流对喷口坐标系内一点的压强为

(12)

其中,εj表示镜反射系数,(1-εj)表示漫反射系数.j=a,i分别对应原子、离子.对上述压强公式进行积分即可得到帆板受到的压力为

(13)

目标受到的羽流消旋力矩为

(14)

其中,Ω为目标帆板上的积分区间,式(14)为等离子羽流消旋力矩理论模型.

2 消旋力矩模型简化

对复杂翻滚运动状态的目标进行消旋,羽流指向点的选择决定了消旋的效率.指向点选择的优化算法求解十分依赖消旋力矩的计算时间,但等离子羽流消旋力矩理论模型存在多次积分运算,求解耗时较大,无法满足实时计算的需求.因此,本文使用神经网络结构来简化消旋力矩理论计算模型,提高消旋力矩计算效率.

2.1 模型简化方法

神经网络结构可以通过大量的训练数据对非线性、高维度的函数进行拟合.神经网络主要由输入层、隐藏层和输出层构成,输入和输出层的节点数由输入数据以及输出数据的数量决定.隐藏层及其节点可以通过经验法进行选择.一般选用单隐藏层神经网络,其节点数可由式(15)计算得到

(15)

其中,Ni是输入层节点数即输入变量的数量,No是输出层节点数即输出变量的数量,Ns为训练的样本数,α为常值取2～10.

本研究通过调节失效卫星绕自旋转动轴的角度与等离子羽流在帆板内的指向位置建立训练集,神经网络的输入为目标的自旋角度θz、羽流指向点在帆板内部长度与宽度方向的位置分别是L1与L2,输出为消旋力矩大小,指向位置如图3所示.共获得42 025个“相对位置与指向-消旋力矩”训练样本,将数据集的70%作为训练集,分别选取15%作为验证集与测试集.使用表1内参数训练神经网络.

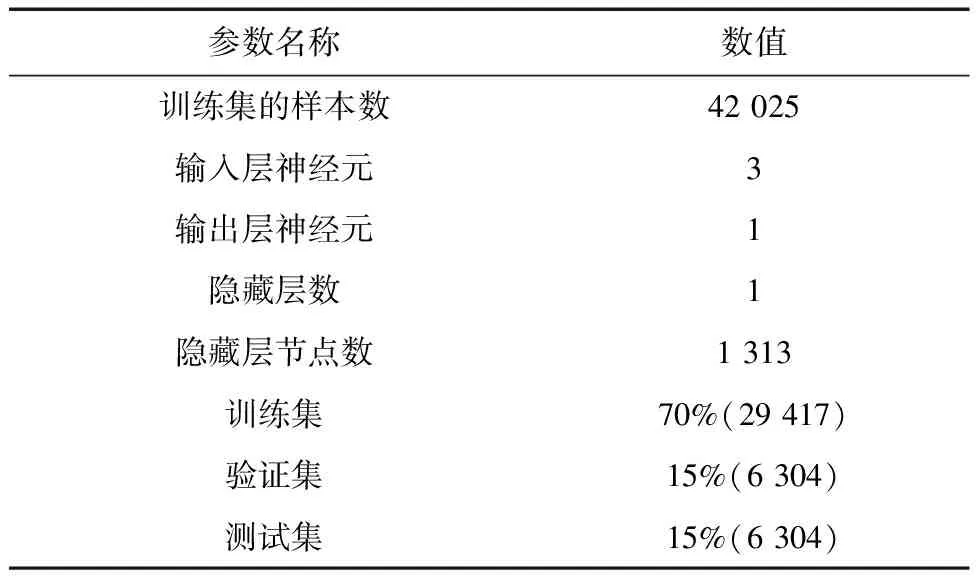
表1 神经网络拟合参数Tab.1 Neural network fitting parameters

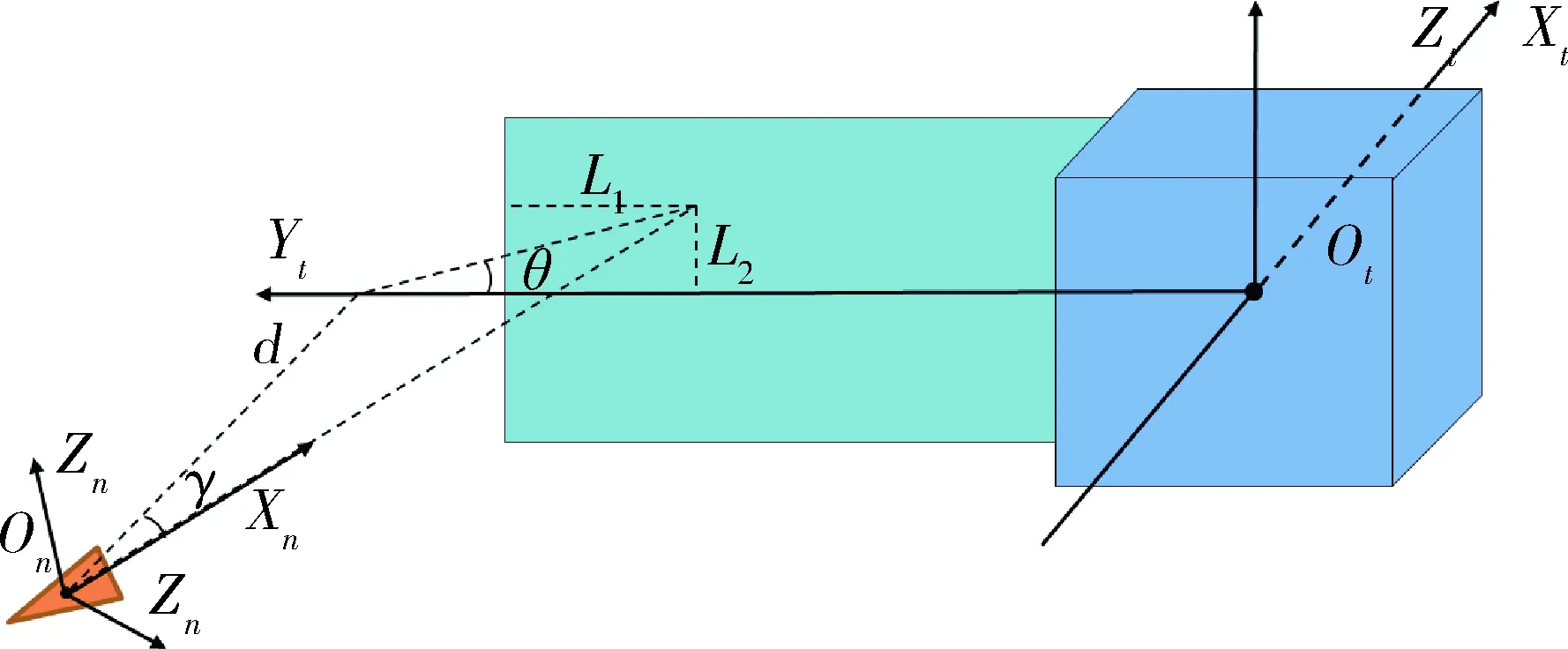
图3 消旋相对位置示意图Fig.3 Schematic diagram of detumbling relative position

本研究对三轴消旋力矩进行拟合,训练结果以相对自旋轴的消旋力矩为例.其中均方误差(mean squared error,MSE)越小,表示拟合误差越小,拟合效果越好.R衡量输出与目标之间的相关性,R接近1代表紧密关系,接近0代表关系随机.如表2所示神经网络模型输出与理论模型输出的相关性参数在1附近且MSE参数接近0,因此神经网络模型的输出与训练样本具有良好的相关性且拟合误差小.

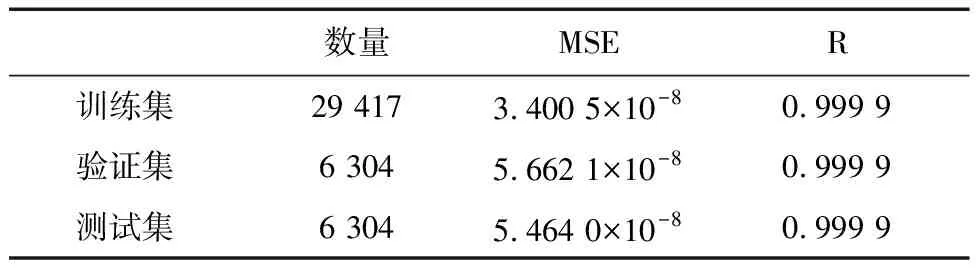
表2 神经网络拟合结果Tab.2 The training results

2.2 快速计算模型仿真

通过设置失效卫星绕主轴转动角度为0°,改变羽流指向帆板内不同点对神经网络快速计算模型进行测试.当羽流指向点在帆板宽度中线时选取41组数据作为仿真测试组.

对比结果如图4所示,理论模型与神经网络模型的力矩变化趋势相同,曲线吻合较好.如图5所示,41组数据的最大误差仅为0.001 6 N·m,精度达到理论模型结果的99%以上.而神经网络模型的计算时间为0.008 3 s,比理论模型(1.411 9 s)快170倍.因此使用神经网络构建的快速计算模型在大幅度提升计算效率的同时具有较高的精度可靠性,可以代替理论模型进行计算.

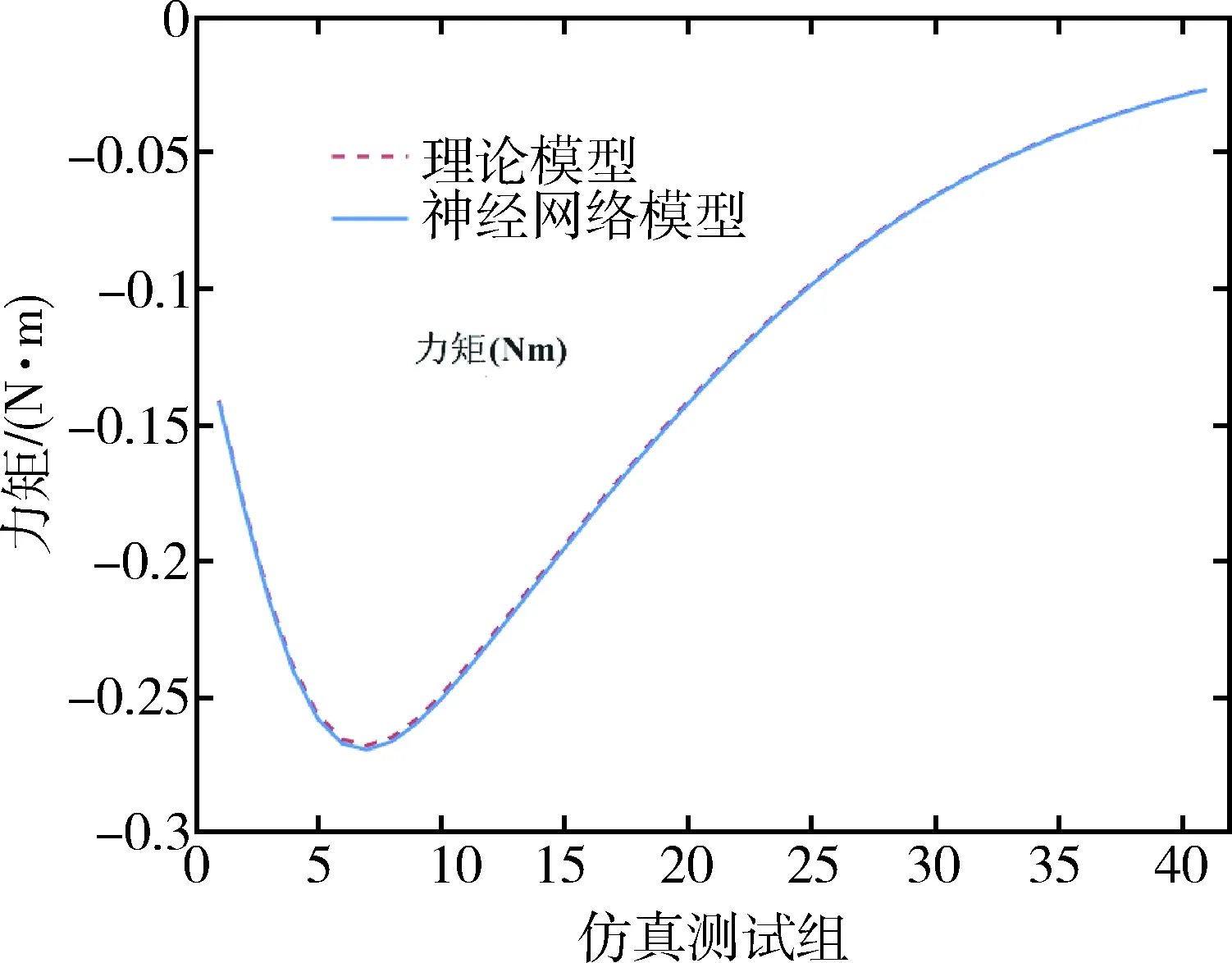
图4 神经网络模型与理论模型测试结果对比Fig.4 The comparisons of the results by neural network model and theoretical model

图5 神经网络模型与理论模型计算误差Fig.5 The Calculation errors of neural network model and theoretical model

3 最优制导律设计

针对失效卫星的自由翻滚运动状态,自旋和章动的耦合消旋十分重要.本节分析了失效卫星的复杂运动状态,定义了章动角速度与章动抑制原则,提出了自旋章动耦合消旋最优制导律.

3.1 章动角速度定义

定义目标的转动惯量I=diag{Ix,Iy,Iz}满足下式

(16)

在目标体坐标系中角速度ω=[ωxωyωz]T分解情况如图6所示.

图6 角速度分解示意图Fig.6 Schematic diagram of angular velocity

如式(16)所示,Zt为最大惯量轴,因此ωz为自旋角速度.ωnut为角速度ω在XtOtYt平面投影,表示目标绕自旋角速度转动的角速度,称之为章动角速度.可由下式计算得到

(17)

3.2 章动抑制原则

在自旋角速度衰减的同时满足章动抑制原则就可以实现目标的自旋章动耦合消旋.因此本节对章动抑制原理进行分析,推导章动抑制原则.

定义章动角速度相关量为

(18)

其中,V为正定变量,其对时间的导数为

(19)

将式(1)中的角速度ωx与ωy表达式代入式(19),可得

(20)

在目标受消旋力作用阶段,式(20)表示的角速度相关量的变化为

(21)

其中,ts、te分别为力矩施加的开始与结束时间,Vc=(Iy-Iz)/Ixωxωyωz+(Iz-Ix)/Iyωxωyωz.式(21)由两部分组成:第一部分为外力矩作用产生的章动角速度变化;第二部分Vc表示目标自身的运动规律,其会导致角速度数值上的增大或减小,但对于目标的整体角动量不产生影响只表示角动量在章动与自旋间的相互转变,不引发章动角速度的实质变化.因此,由消旋力矩产生的章动角速度变化量可表示为

(22)

为保证章动角速度衰减,其变化量应满足ΔVτ<0,代入式(22)可得

(23)

在消旋力执行阶段只需目标受到的消旋力矩满足上式,就可实现章动角速度衰减,由此可以得到章动角速度抑制原则如式(23)所示.

3.3 自旋章动耦合消旋制导律设计

传统消旋制导律需要消旋力矩满足式(24),实现每个方向角速度同时衰减

(24)

但是针对不同消旋场景,式(24)限制过于严格,不能实现高效消旋,因此就需要设计一种多任务场景自适应的等离子羽流指向点的选择方法,实现失效航天器的高效消旋.因此,建立自旋章动耦合消旋最优制导律为

其中,α=ωz/ω0z、β=k(1-α)为自旋章动耦合消旋参数,sign(x)为符号函数,ω0z为目标初始自旋角速度.k为常数,其选择与等离子羽流撞击帆板产生的章动消旋力矩与自旋消旋力矩之间的比例有关,当k值较小时制导律偏向章动消旋,k值较大时制导律更偏向自旋消旋.式(25)的解为羽流在帆板内的最优指向点,由帆板内可产生的最优消旋力矩得到.

制导律约束第一项ωxτx/Ix+ωyτy/Iy<0为章动抑制原则.约束ωzτz/Iz<0表示自旋角速度消旋约束,在消旋过程中自然满足.通过章动与自旋两项约束就可以实现自旋章动耦合消旋.代价函数J中使用角速度的符号以及目标转动惯量对三轴消旋力矩进行加权,同时使用自旋角速度的变化分别对章动角速度部分以及自旋角速度部分进行加权.通过上述两次权重设计向制导律引入失效航天器自身状态以及运动状态,实现失效航天器的高效自旋章动耦合消旋.

为减少等离子羽流消旋过程中的能量消耗、适应服务航天器自身的控制能力,本文结合消旋执行条件设计了基于最优制导律的自旋章动耦合消旋策略如图7所示.为降低消旋过程中对控制的需求,服务航天器不随目标转动只在小范围内移动,且仅在失效航天器的姿态满足消旋执行条件时进行羽流消旋,提高消旋效率.

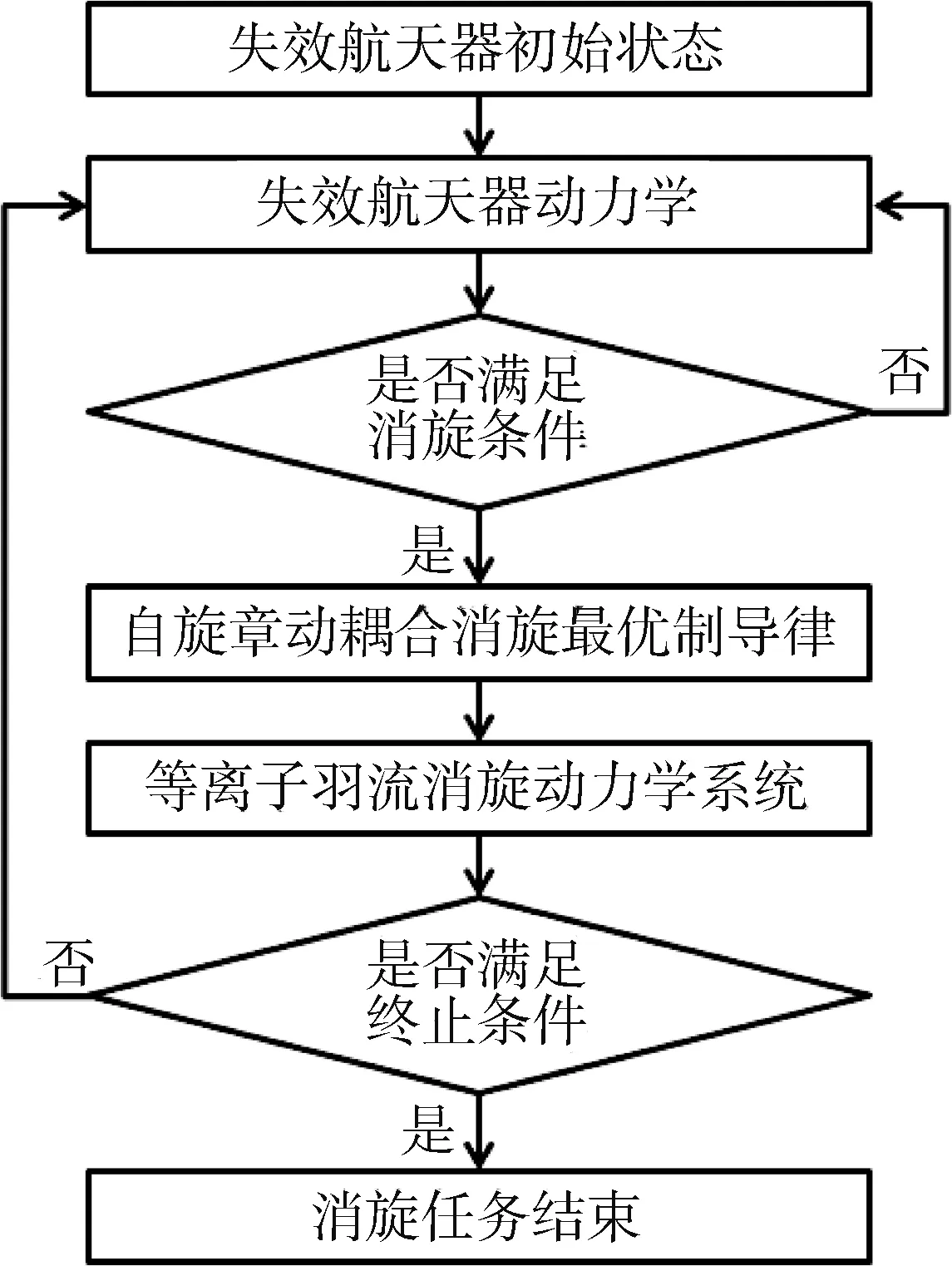
图7 消旋策略流程图Fig.7 The diagram of detumbling strategy

4 仿真分析

4.1 自旋章动耦合消旋可行性分析

等离子羽流消旋的原理是通过微观粒子撞击失效航天器的帆板产生消旋力矩进行消旋,帆板形状以及羽流指向点会影响章动消旋力矩的大小,因此本节对等离子羽流产生的消旋力矩进行仿真计算,对其中的章动消旋力矩的大小及变化趋势进行分析,验证自旋章动耦合消旋的可行性.

失效航天器的单侧帆板大小设置为8 m×2 m,服务航天器与在失效航天器的质心轨道坐标系内位置为[-4,9,0].等离子羽流仿真参数如下:霍尔推进器外径0.3 m,内径0.1 m,玻尔兹曼常数为1.38×1023,粒子从喷口出发的速度为2×103m/s,喷口处温度为1 500 K,氙原子质量为2.2×10-25kg,氙原子数密度为1.26×1017m-3,目标处温度为500 K.目标帆板的镜反射与漫反射参数均为0.5.

当目标主轴角度为0°时在帆板内部分别选取指向点[6,0]、[6,0.5]、[6,-1]进行验证.图8展示了在羽流指向点不同时失效卫星帆板处的压强大小云图.表3为3种不同情况的消旋力矩仿真结果.

图8 压强仿真结果Fig.8 Results of pressure simulation

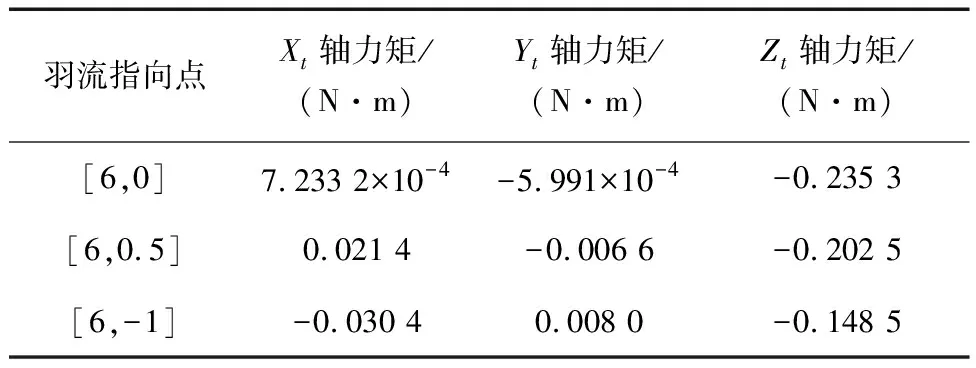
表3 力矩仿真结果Tab.3 The training results of pressure

其中情况一为羽流指向帆板[6,0]点处,观察图8(a)压强主要分布于帆板中线附近,即其产生的力矩大小为-0.235 3 N·m主要针对Zt轴,其余两轴受到的消旋力矩大小在0附近,因此当羽流指向帆板中线时只进行自旋消旋.

情况二与情况三的羽流指向点分别为[6,0.5]与[6,-1].其中相对章动的最大消旋力矩的绝对值分别约为自旋轴消旋力矩的11%、21%,能够产生有效的章动消旋力矩.测试组中章动消旋力矩的大小随指向点的选择而变化,指向点越靠近帆板外侧其绝对值越大.而无论羽流指向点的选择如何变化,均能产生针对自旋的消旋力矩,但其大小会随着指向点向帆板外侧靠近而减小.由此,选择不同的羽流的指向点改变章动消旋力矩与自旋消旋力矩的比例实现自旋章动耦合消旋.

4.2 最优制导律仿真分析

进行失效航天器复杂运动消旋仿真可以直接验证最优制导律消旋的高效性.服务航天器相对位置与消旋力矩仿真中参数设置相同,当目标自旋角为-30°～0°时执行消旋.仿真分析中失效航天器的质量为200 kg,其转动惯量为tI=diag{700, 820, 1 100}kg·m2,初始角速度为(1,0,6)(°)/s,参数k取1/100,使用遗传算法对制导律进行求解,考虑实际任务中羽流指向的精度问题,使用均值为1,方差为0.01的白噪声对最优消旋力矩加权进行拉偏处理,仿真结果如图9和图10所示.

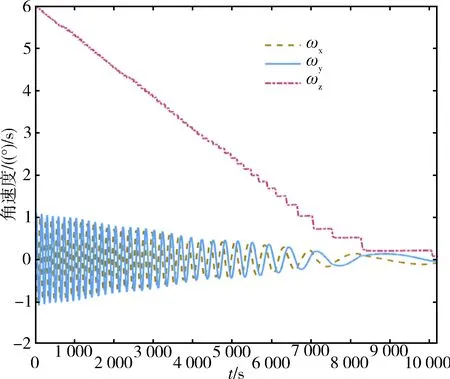
图9 等离子羽流作用下的目标角速度演化Fig.9 The target angular velocity under the plasma plumes detumbling

图10 目标角动能变化曲线Fig.10 The curve of target angular kinetic energy

由仿真结果可知,在10 199 s后等离子羽流将目标自旋角速度从6(°)/s稳定至0.05(°)/s以下,目标章动角速度从1(°)/s稳定至0.006(°)/s以下,完成了目标的自旋角速度与章动角速度消旋.

使用上述仿真参数对现有的消旋制导律进行仿真,其可以实现自旋角速度消旋但是会导致章动角速度发散.而如图10所示,使用本文的提出的最优制导律,章动动能与自旋动能衰减的变化趋势相同,可以实现自旋章动耦合消旋.

图11与图12分别为使用最优制导律消旋过程中目标三轴受到的消旋力矩大小以及羽流指向点位置.结果表明,在消旋初期羽流指向点分布于帆板宽度方向两侧,随着章动角速度的衰减,指向点向帆板中线靠拢.由于羽流指向点的变化,Xt轴与Yt轴的消旋力矩随着章动角速度的减小逐渐减小,而自旋轴的消旋力矩逐渐增大.指向点以及消旋力矩随着消旋过程中目标角速度变化而改变验证了上述最优制导律可以将目标状态引入消旋策略设计中,实现高效的章动耦合消旋.

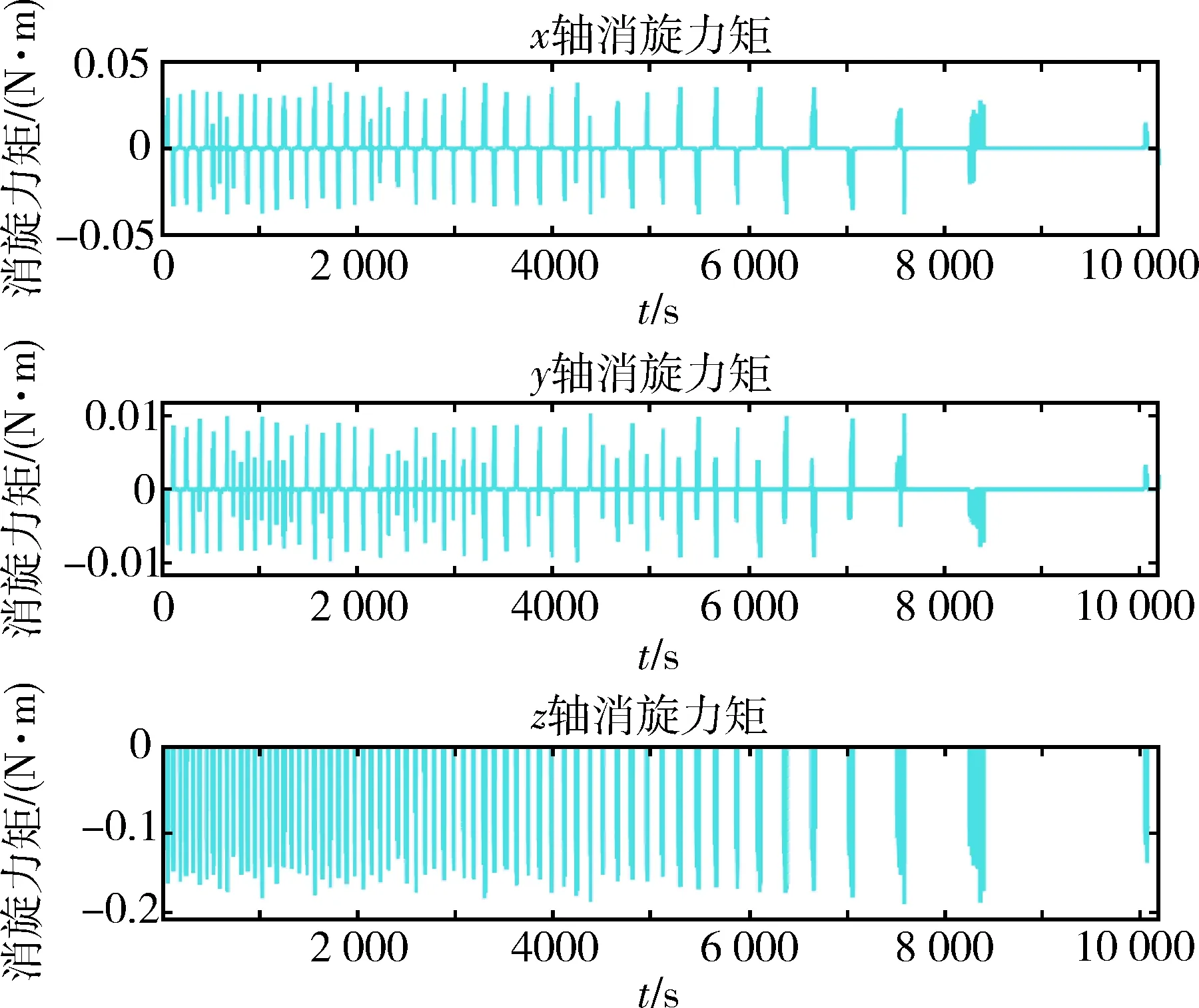
图11 目标受到的三轴消旋力矩Fig.11 Three-axis detumbling torque of target

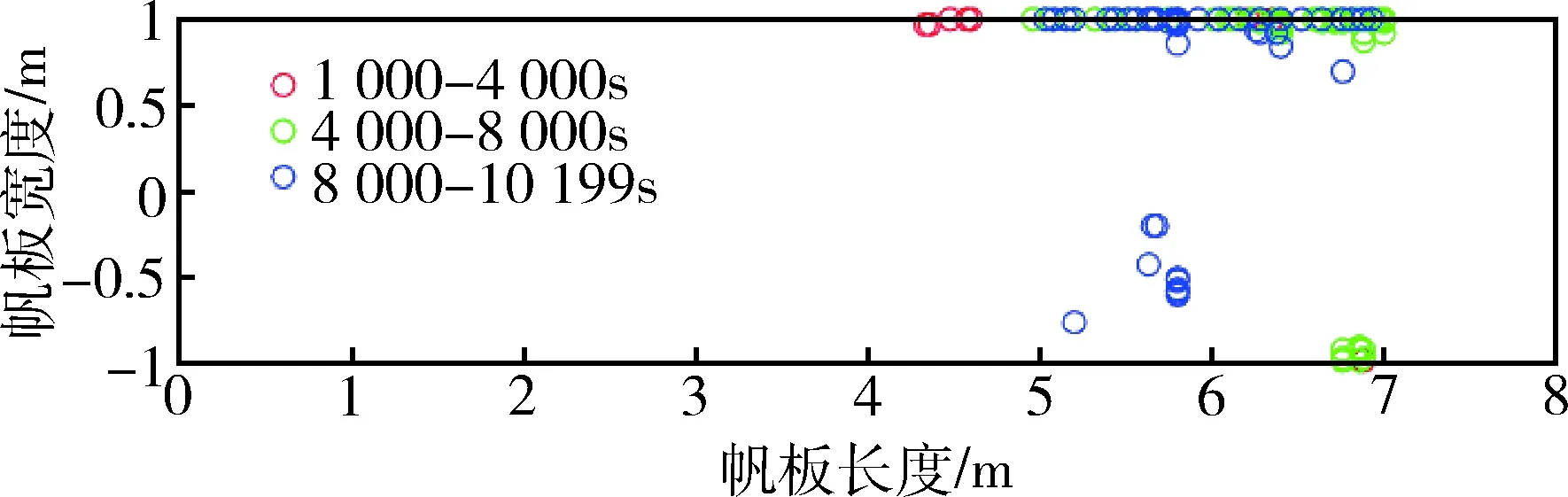
图12 消旋过程中羽流指向点分布图Fig.12 Plume pointing point distribution map of detumbling

5 结 论

为克服传统羽流模型复杂,计算耗时长的问题,本文基于神经网络建立了等离子羽流消旋力矩的快速计算模型,在几乎不损失精度的情况下将计算效率提升2个数量级以上.本文提出了一种自旋章动耦合消旋最优制导律,以应对目标复杂的运动状态,并通过失效航天器消旋仿真分析上述制导律的可行性与高效性.仿真结果表明该制导律3 h内能够将6°自旋角速度以及1°章动角速度降至10-2量级以下,实现了自旋章动协同消旋以及目标状态的稳定,验证了本文提出的制导律能够完成目标自旋与章动运动的耦合高效消旋.