基于码道三角波骨架提取的量子点光栅尺高精度测量方法

吴志良 ，蔡念 ，欧伟程 ，陈晓娜 ，王晗

（1 广东工业大学 信息工程学院， 广州 510006）

（2 广东工业大学 机电工程学院， 广州 510006）

0 引言

高端微纳制造与测量是先进制造领域的重要研究方向，受到国际学术界和工控产业界的高度重视［1］。如何实现高精度位移测量是高端制造装备制造的关键环节［2-6］。目前，激光干涉仪和光栅尺常被用于高精度位移测量［7-10］。前者可通过计数和细分干涉条纹实现亚微米级测量，但对测量环境要求苛刻［11-12］，且光学零件繁多难以直接集成于装备内部，极大地限制了其在工业测控领域的应用。相对于激光干涉仪，光栅尺［13］具有低成本、小体积、高精度的优点，被作为核心位移测量器件而广泛集成于精密制造装备。当今，大批量稳定制造光栅的方法主要有机械刻栅、光刻刻栅等［14-20］。可是，这些成熟工艺具有成品率低，生产周期长、生产条件严苛等缺点。而且，采用这些工艺制造出来的光栅尺在长时间运作后，光源模块会产生大量热导致光栅尺内部温度变化剧烈，引起光栅基底（即码道）的热形变误差，影响其测量精度［30］。为了规避现有光栅尺的制栅工艺缺陷，本研究团队采用微纳增材制造开发出一款新型量子点光栅尺［31］，其工作原理是将增材制造喷印在基底上的自发光量子点码道图案作为信息载体，运用机器视觉方法对该连续、规则、蜿蜒的量子点码道图案进行实时处理而实现位移测量。

类似于现有光栅尺测量，量子点光栅尺在测量过程中也不可避免地会受到测量硬件偶然误差（如尺身污染、光电不稳定性、工装误差）、外界温度、振动等因素的干扰［23-26］，从而影响测量精度。已有不少研究探索测量方法和误差抑制方法，以提升现有光栅尺的重复定位与绝对定位精度［27-30］。李彦锋等［27］利用基于虚拟仪器的宏微复合光栅尺测量系统代替莫尔条纹的电子细分方法。CAI N等［28］利用经验模态分解方法分解出本征模函数来描述轮廓变化的趋势，进而得到一个自适应阈值以划分光栅精细边缘。LI W等［29］基于经验模态分解和局部正弦辅助方案提出一种光栅尺非线性误差补偿方法，提升了绝对式光栅尺测量精度。BARAKAUSKAS A等［30］建立一种新的数值模型解决光栅尺在非理想环境下的振动误差。但是，量子点光栅尺的量子点码道图案与现有光栅尺的黑白相间光栅条纹在外观上具有极大的差异性，前者表现为连续且规则的蜿蜒形状，因此难以将现有光栅尺的测量方法直接应用于量子点光栅尺。

为进一步提高量子点光栅尺的测量精度，本文提出一种基于码道三角波骨架提取的量子点位移测量方法。采用不定步长边缘跟踪方法快速、有效地检测出量子点光栅尺码道边缘。为了确保算法稳定性和较好的细分线性度，采用三角波拟合方法提取量子点光栅尺码道骨架。采用一种由粗到精的位移检测方法，准确地进行位移测量。最后，采用径向基神经网络进行非线性测量误差补偿，减少绝对位移误差。

1 量子点光栅尺简述

图1为量子点光栅尺的内部结构及其测量工作原理。图2为量子点光栅尺光信号采集系统，采集的码道呈现连续、规则的蜿蜒形状，在365 nm波长的紫外光线照射下实现光致发光。在文献［31］中，采用机器视觉方法对码道图案进行处理实现高精度测量，即简单地对粗位移值与精位移值两个数据量进行同步解耦：采用蜿蜒波峰个数累加法获得粗位移值，采用像素点细分方法获得细位移值。虽然这种位移测量方法已经达到设计要求［31］，但是仍然距离高精度需求较长距离。因此，本文提出一种新的高精度位移测量方法，进一步提升量子点光栅尺的测量精度。

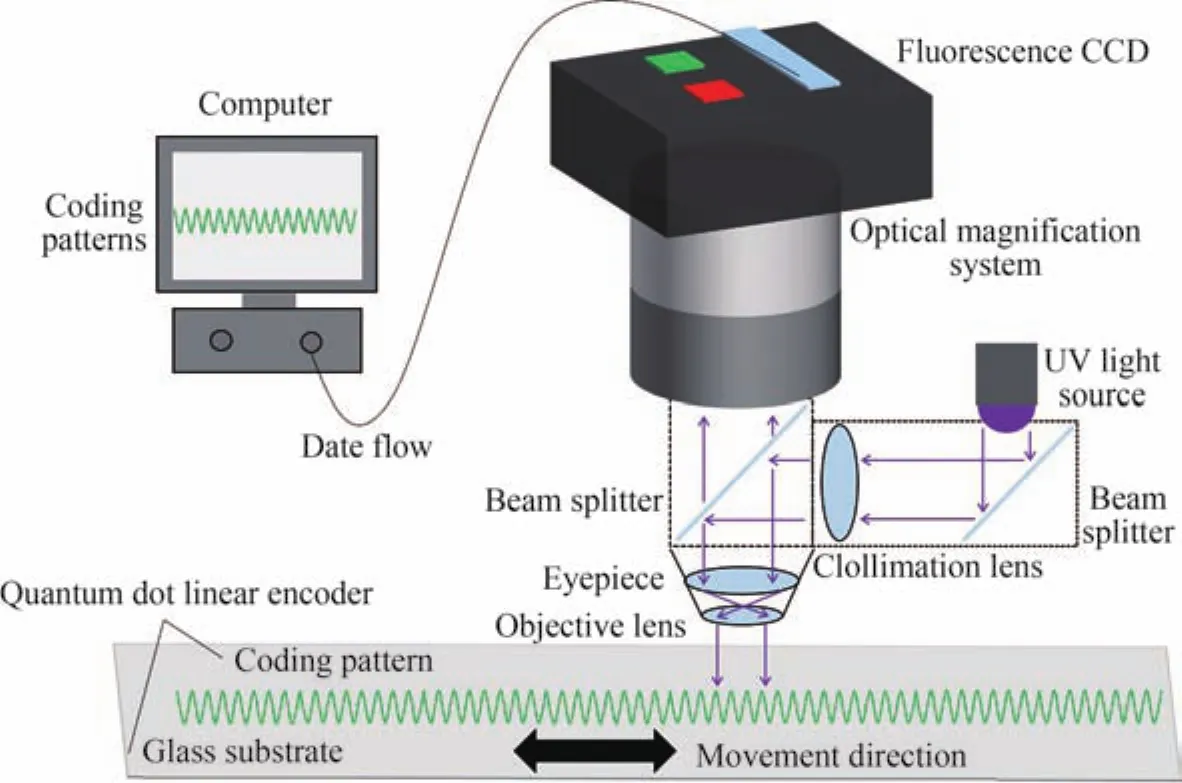
图1 量子点光栅尺的位移测量原理［31］Fig.1 Displacement measurement principle of quantum dot encoder［31］

2 方法与理论

本文提出的量子点光栅尺位移测量方法主要包括码道图像预处理、码道检测、码道骨架提取和位移测量等四个步骤，如图3所示。首先对采集到的码道图像进行自适应二值化预处理；然后提出不定步长边缘跟踪方法检测码道轮廓；之后，由码道轮廓获得码道中线，采用三角波对码道中线进行拟合得到码道骨架；最后，在位移测量步骤，先采用宏微复合测量方法分别测量码道粗位移值和精细位移值，再采用径向基神经网络进行非线性误差补偿，最终获得精确位移值。

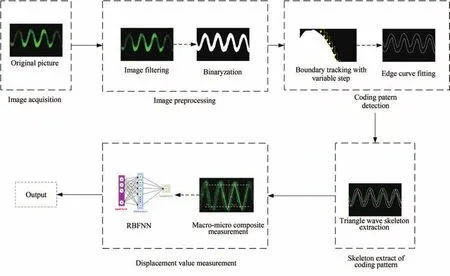
图3 位移测量方法流程图Fig.3 Pipeline of the proposed measurement method

2.1 基于不定步长边缘跟踪的码道检测

考虑到量子点光栅尺码道呈现蜿蜒状且连续的形状特性，提出不定步长边缘跟踪方法检测码道上下边缘（如图4所示）。相比于传统边缘跟踪算法，不定步长边缘跟踪方法在边缘跟踪方向判断时只需判断右上和右下两个方向，大大加快了边缘跟踪速度。为了进一步提升算法效率，先检测出离散边缘点再拟合出完整码道边缘。需要注意的是，相比于码道的其他位置，在码道波峰及波谷处需设计较小的检测步长，以实现码道波峰波谷的精确检测。以上边缘跟踪为例，对不定步长边缘跟踪方法进行概述。

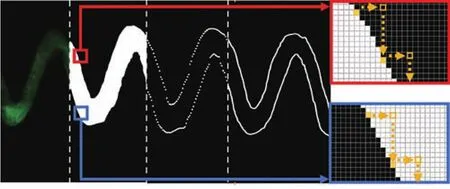
图4 码道轮廓检测Fig.4 Contour detection of the coding pattern

1）确定起始点。对一张二值化码道图像，从待检测区域的最左上角像素开始，往下扫描找到第一个像素值为255的点为起始点，记为P0(x0，y0)。

2）确定下一个边界点。记P1(x1，y1)=(x0+1，y0+1)。若P1=0，则码道边缘位于P1右下方，此时先由P1向右搜索至P2(x1+n，y1)，再一直往下搜索至检测区域下边界，找到第一个像素值为255的点，记为P3；若P1=255，则码道边缘位于P1右上方，此时P1向右搜索至P2后再一直往上搜索至检测区域上边界，找到最后一个像素值为255的点，记为P3。

3）逐点跟踪。将P3标记为P0，重复步骤2），直至搜索点到达检测区域的右边界或下边界则跟踪停止，获得码道边缘离散点［xi，yi］（i=0，1，2，…，n）。

4）码道边缘连接。首先计算步长hi

然后将边缘离散点以及步长hi，代入

将式（2）求解得到的mi代入

求解式（3）～（6）获得样条曲线系数ai，bi，ci，di。则任意两个邻近离散边缘点xi和xi+1，采用式（7）获得两者之间的插值gi(x)即可获得连续边缘值

2.2 基于三角波拟合的码道骨架提取

经过2.1节所述码道边缘检测方法后，分别得到码道上、下边缘像素坐标序列yul(x)和ydl(x)。考虑到光栅尺的高速测量，提出一种简单高效的码道中线提取方法得到码道中线yml(x)，

在量子点光栅尺制造时，采用四轴运动平台按照设计移动光栅尺基底，使得喷头打印或喷印在基底上的量子点呈现连续、规则、蜿蜒的码道图案。因为运动平台自身限制，其运动轨迹更趋向于三角波方式行进，所以对码道中线用最小二乘法进行三角波拟合后得到码道骨架，如图5所示。

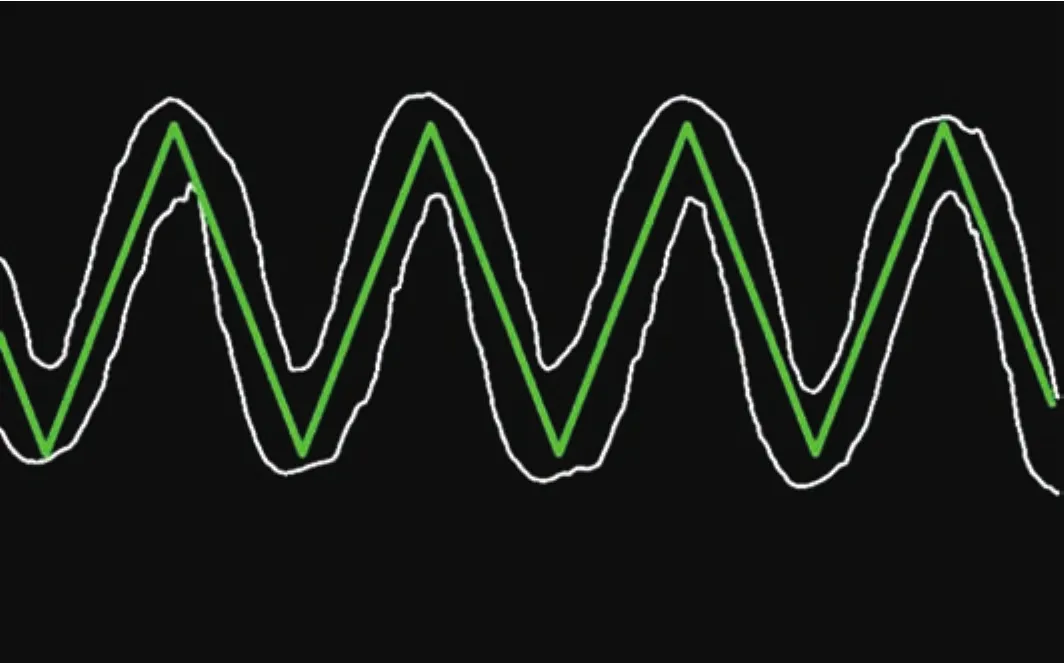
图5 码道骨架提取Fig.5 Skeleton extraction of the coding pattern

具体实现如下：对码道中线共m个样本点数据（xi，y）i进行三角波拟合，即

如式（9）拟合的数据满足则三角波拟合得到码道骨架。

虽然这种三角波拟合的码道骨架提取方法能够满足光栅尺测量的时效性，但是会产生一定的测量误差，因此在后面将引入快速非线性误差补偿来提升测量精度。

2.3 位移测量

对码道骨架采用由粗到精的码道位移计算方法计算位移值Nxs

式中，Nx1、Nx2分别为码道粗位移值和细位移值，将在下面进行阐述。

2.3.1 码道粗位移值

待量子点光栅尺归零后，将图像最清晰区域作为感兴趣区域（Region of Interest， ROI），将ROI内最左边的码道骨架波峰对应的x轴坐标x0所在列作为固定观测位，如图6白色竖直虚线所示。当量子点光栅尺发生位移时，码道骨架的波形相位也会相应发生变化，此时x0位置对应的y值也会发生变化（如图6右图所示）。为提高解码的抗干扰能力，降低误码率和丢码率，设立上下两个阈值Yu和Yd。当且仅当观测位（x0，y）的y值先小于Yd，再大于Yu，认为码道位移经过了一个码元。

图6 位移测量Fig.6 Displacement measurement

式中，Lp为码元长度。

2.3.2 码道精细位移值

精细位移值Nx2根据观测点距离最近波峰的长度来决定，即

式中，xNx1为距离观测位（x0，y）最近波峰的x轴坐标，Lpix为每个像元的物理长度。

2.3.3 位移非线性补偿

对同一码道进行多次测量，得到n组测量数据Nxn s，即可获得测量平均数据。

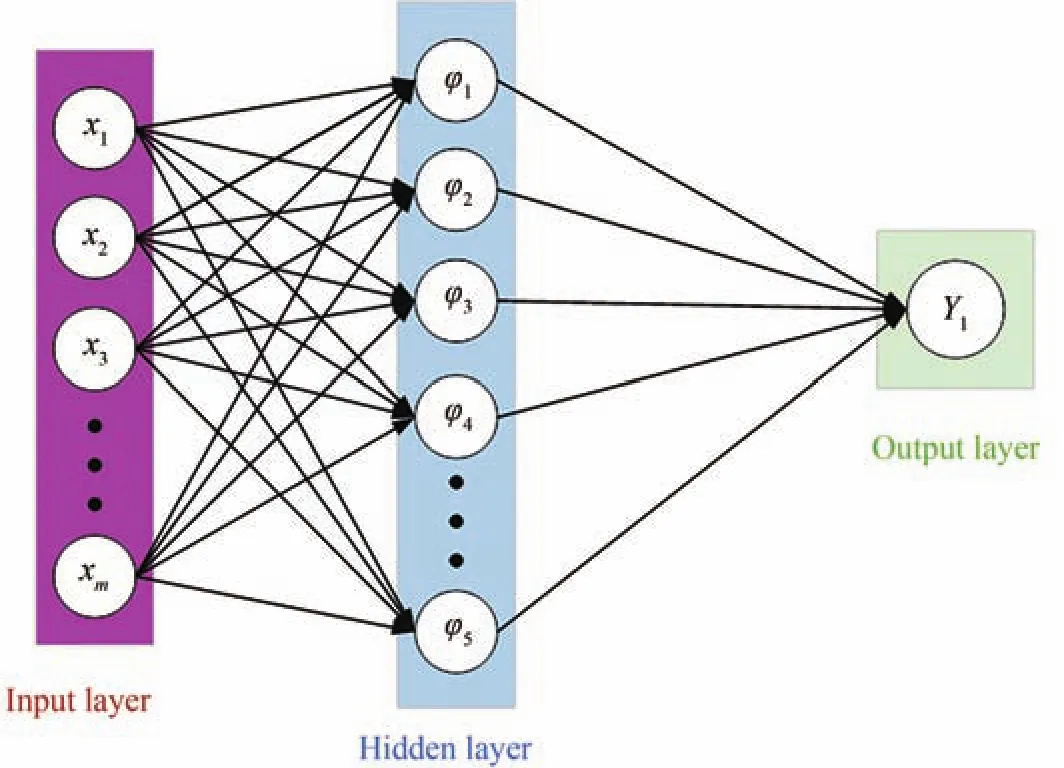
图7 径向基神经网络Fig. 7 Radial basis function neural network

式中，xc和σ分别为径向基函数φ（x）的核和方差，经过网络训练确定其参数值。后续测量将位移值Nxs直接输入到训练好的径向基神经网络，进行非线性误差补偿获得量子点光栅尺的精确位移值。

3 实验

3.1 实验平台

量子点光栅尺选用荧光CCD组件（广州明美，Mshot MS23）作为光信号读数头，在完成荧光CCD与码道的对焦后即实现量子点自发光图像采集。随后，将高精度直线电机（美国AREOTECH，ABL1500）作为光栅尺的运动载体进行定向运动，直线电机通过螺栓固定于大理石气浮平台上，避免外界与人为制造的过大抖动引入外界干扰误差。使用激光干涉仪（型号为Keysight 5519系列，定位精度±0.1 μm）作为参照标准。实验在黑暗遮光罩内执行，实验温度为20 ℃。量子点光栅尺测量系统如图8所示，位移测量方法执行硬件和软件环境配置如表1所示。

表1 位移测量方法执行硬件和软件环境配置Table 1 Hardware and software environment configurations of the displacement measurement method

图8 量子点光栅尺测量系统Fig.8 Measurement system of the quantum dot encoder

3.2 评价指标

为了客观地验证本文方法，使用均方根误差（Root Mean Square Error，RMSE）、误差绝对值的最大值（Max Error）及方差（Variance）、重复定位误差（Rep Error）、95% 置信区间（Confidence Interval，CI）、运行时间（Running time）这六个指标进行评价。重复定位误差表示量子点光栅尺在同一位移距离下测量值之间的偏移值。均方根误差计算公式为

式中，h(xi)表示位移测量算法输出的测量值，yi表示用激光干涉仪测量出的基准值。

置信区间计算公式为

式中，lower表示置信区间下限，upper表示置信区间上限，Mean为平均定位误差，ST为测量误差的标准差。

当取95%置信区间时，z值为1.96。

3.3 波形拟合讨论

为了验证三角波拟合的有效性，采用最小二乘法分别将码道中线拟合成三角波、正弦波和方波，拟合效果如图9所示，对测量影响如表2所示，其中RMSE表示拟合波形与码道中线的均方根误差。从表2可知，三角波拟合后的测量信号幅度最大，其测量信号的均方根误差远小于方波拟合而稍大于正弦波拟合。RMSE过大表明拟合后的波形发生了严重失真，如图9（c）的方波拟合信号所示。

表2 波形拟合结果对比Table 2 Comparisons of fitting results via different waveforms

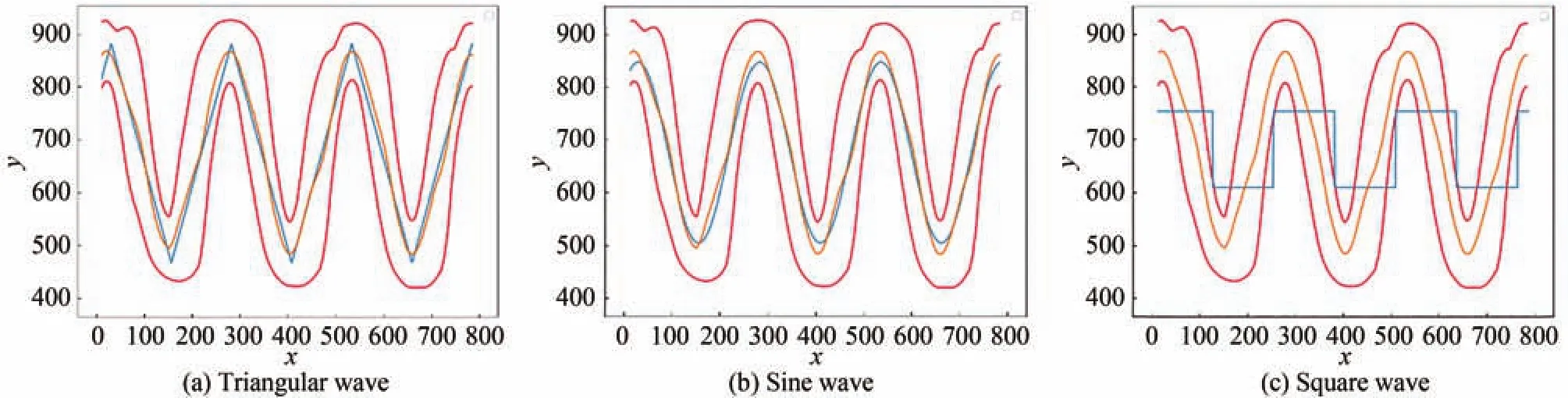
图9 波形拟合对比Fig.9 Comparisons of different waveform fittings

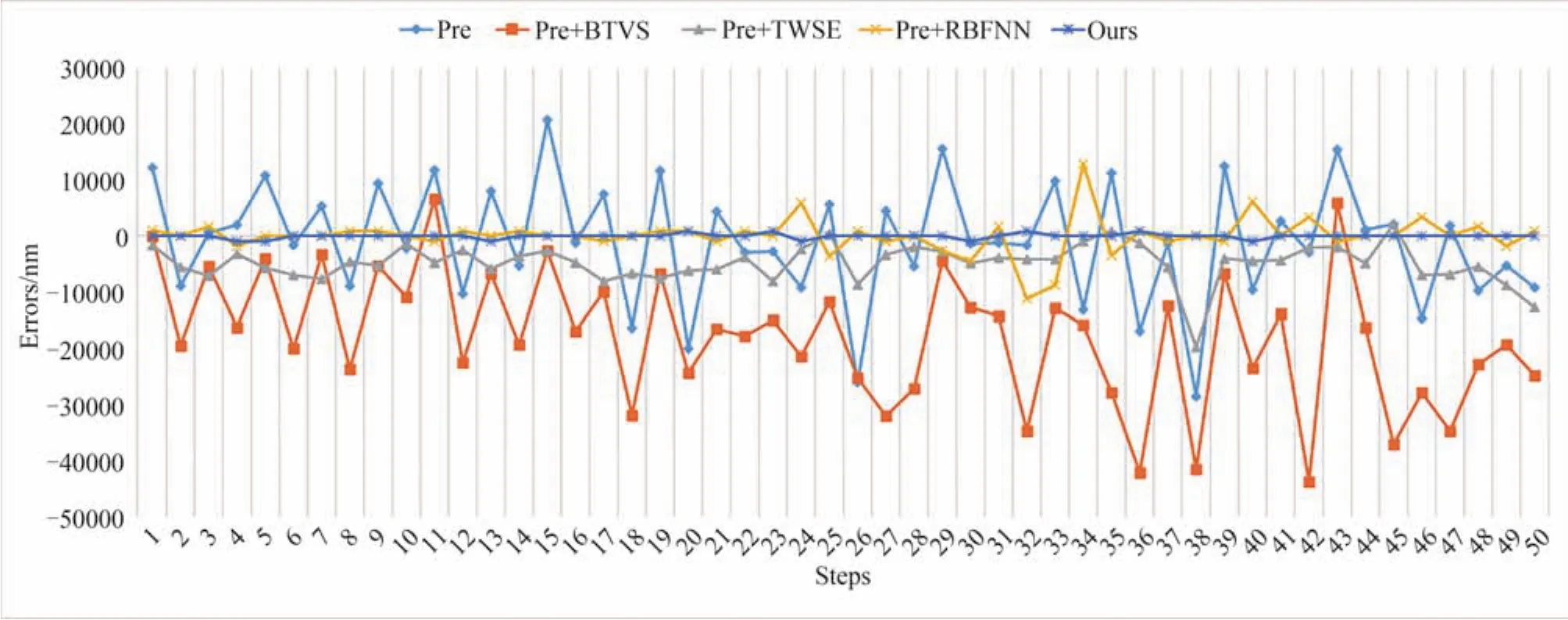
图10 各方法误差对比Fig.10 Measurement errors obtained by five methods

由于在实际测量中阿贝误差和余弦误差［21］的产生是难以避免的，将造成量子点光栅尺的码道发生相对位置偏移。当码道竖直方向偏移过大，造成拟合后的波峰低于图6所示的上阈值Yu，或波谷高于Yd时就会产生丢码。同时，上下阈值之间不宜设置得过于接近，以防止测量中因抖动而产生误码。因此更大的幅值可以使得上下阈值有更广的设置范围，从而降低误码率。因此，在三角波与正弦波的均方根误差相差不大的情况下，本文选择幅值更大的三角波拟合测量信号。

3.4 神经网络对误差补偿的作用

为了验证径向基神经网络对量子光栅尺测量误差补偿的作用，在其他实验条件不变的前提下，使用Back Propagation（ BP）网络、长短期记忆网络（Long Short-Term Memory，LSTM）网络以及径向基神经网络分别对测量位移数据进行补偿处理。由表3可以看出，径向基神经网络在误差补偿性能上优于其余两个神经网络。

表3 不同神经网络用于量子点光栅尺误差补偿Table 3 Comparisons of error compensation for the quantum dot encoder via different neural networks

3.5 消融实验

本节进行消融实验分析提出的位移测量方法中的三个不同步骤对位移测量的影响。以文献［31］的位移测量方法为基础方法，增加不同步骤以说明各自对位移测量的影响。为了方便描述，将基于不定步长边缘跟踪的码道检测简称为BTVS（Boundary Tracking with Variable Step，BTVS）；基于三角波拟合的码道骨架提取检测简称为（Triangular Wave Skeleton Extraction，TWSE）；径向基神经网络简称为RBFNN（Radial Basis Function Neural Network，RBFNN）。同时，我们重复了10组对比实验进行统计分析。

1） BTVS步骤讨论

BTVS的检测路径一直保持在码道边缘周围，因此只需要遍历很少的像素点即可检测出边缘。从表4可以看出，当融入BTVS时，基础方法的运行时间可以从42.13 ms缩减到20.17 ms，运行效率提升了108.86%。

表4 消融实验Table 4 Ablation experiments

2） TWSE步骤讨论

当基础方法增加了TWSE之后，除了运行效率略有下降，其余指标均得到提升。这是因为使用三角波拟合得出码道骨架后，首先使得码元之间有了精细明确的分界点；其次，由于三角波为一次函数，使得测量结果有较好的细分线性度；最后，因为使用了最小二乘法拟合波形，因此只有当检测出的码道中线在噪声环境下整体或大部分数据发生偏移，才会使得拟合波形发生变化，这使得码道骨架具有较高稳定性，体现在位移测量方法的重复定位误差由±8.695 μm降低到±0.870 μm。

3） RBFNN步骤讨论

当基础方法融入了RBFNN之后，RMSE、Max Error、方差、CI等指标均得到提升，说明RBFNN可以有效地补偿量子点光栅尺非线性误差。

由表4看出，本文提出的位移测量方法大幅度地提升了测量速度，而且各项测量指标远优于文献［31］，这说明本文融合了BTVS、TWSE、RBFNN三个步骤后，综合提升了其测量性能。

4 结论

本文提出了一种基于码道三角波骨架提取的量子点光栅尺高精度测量方法。该方法利用不定步长边缘跟踪方法提升算法运行效率，提取码道三角波骨架增加测量结果的稳定性，最后利用径向基神经网络进行非线性补偿，减少绝对定位误差。实验结果表明，提出的位移测量方法能够实现快速、精确地量子点光栅尺高精度测量。相比于现有位移测量方式，提出的位移测量方法具有更高的测量精度、测量稳定性和测量速度。