NAEP四年级数学“测量”试题分析
2023-07-11高梦雅林子植
高梦雅 林子植

【摘 要】小学阶段作为系统学习测量知识的初级阶段,对培育学生的测量素养起着奠基作用。教师可借鉴国外的成功经验,编制“测量”试题,培养学生的测量素养。为此,教师选取2005—2022年NAEP四年级的“测量”试题,从核心素养、思维模式、问题情境、表征方式四个维度对其进行统计和分析。据此得出,小学“测量”试题的编制需重视以下几点:量感和其他素养协同考查,体现综合性;试题贴近学生生活,体现应用性;加强逆向思维考查,体现发展性;优化表征方式,体现过程性。
【关键词】NAEP;测量;试题表征;量感
一、引言
测量是联系儿童世界和数学世界的重要组成部分,对儿童生活以及儿童素养的发展都具有重要作用[1]。小学阶段作为系统学习测量知识的初级阶段,对培育学生的测量素养起着奠基作用。综观国际数学课程内容可以发现,大部分国家都把“测量”作为一个单独的学习板块,或者以“测量”为主线开展学习,可见“测量”知识对学生发展的重要性。但是,我国义务教育阶段的数学课程内容由数与代数、图形与几何、统计与概率、综合与实践四个学习领域组成[2],小学数学测量知识分散在“图形与几何”“综合与实践”等多个领域,缺乏系统性。因此,我国可借鉴国外的成功经验,思考如何编制“测量”试题,培养学生的测量素养。
美国国家教育进展评估项目(National Assessment of Educational Progress,以下简称“NAEP”)2019年小学四年级数学的评价框架,将小学数学内容划分为数的性质与运算、测量、几何、统计与概率以及代数五大领域,其占比分别为40%、20%、15%、10%、15%。评价框架明确指出,学生在测量领域应该掌握测量属性和测量体系两大内容,具体包括:能够理解长度、温度、时间、面积等测量属性;能够直接测量或估计测量大小、重量等物体属性;能够运用公式简单计算图形的面积或周长;能够认识和理解单位且可以进行单位换算。那么,NAEP四年级的“测量”试题究竟是如何考查的,考查的内容有哪些特点?为此,笔者选取NAEP官网上已公布的2005—2022年四年级的“测量”试题,对其进行统计和分析,旨在为我国小学数学“测量”试题的编制提供借鉴和思考。
二、NAEP四年级数学“测量”试题分析
试题命制过程要兼顾立意、情境、设问和修饰,试题题干语言的表达要简明准确,知识的考查要基于课程标准、聚焦核心素养,并注重数学思想方法[3]。因此,笔者选取2005—2022年NAEP已公布的55道小学数学四年级的“测量”试题,分别从核心素养、思维模式、问题情境、表征方式四个维度对其进行统计和分析。
(一)基于核心素养的试题分析
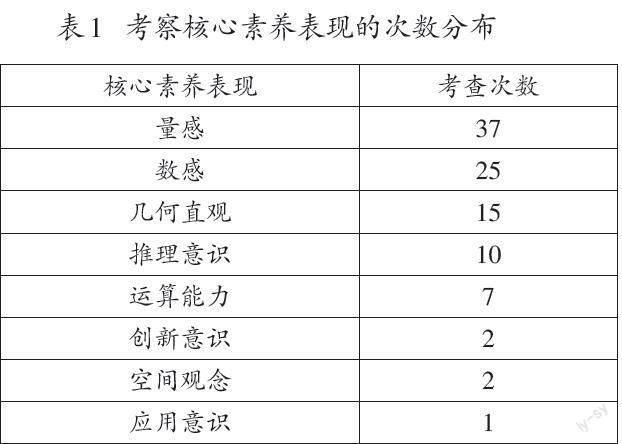
《义务教育数学课程标准(2022年版)》(以下简称《课程标准》)指出,试题命制应考查数学知识和核心素养的相应表现。因此,笔者以《课程标准》中的11个核心素养表现(如量感、数感等)为基础,并咨询多位专家及部分一线教师的意见,从考查核心素养表现的维度,对NAEP四年级“测量”试题进行了统计和分析(如表1)。
统计结果表明,从整体分布上看,55道“测量”试题一共考查了量感、数感、几何直观等8种核心素养表现,一道试题基本上考查了2~3种核心素养表现,主要偏重对量感、数感、几何直观等核心素养表现的考查;从关联程度上看,大部分的试题在考查量感的同时,也考查了数感、几何直观等核心素养的表现。现以具体试题为例,来说明NAEP“测量”试题是如何考查学生的核心素养的。
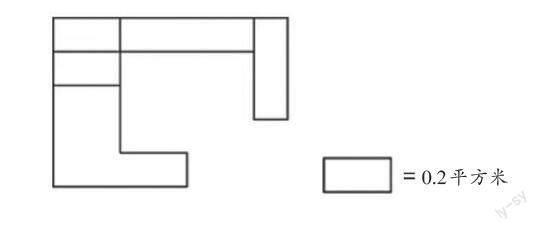
【试题1】(NAEP 2011年)估一估,此图形的面积最可能是多少?
A.小于1平方米
B.大于1平方米,小于1.5平方米
C.大于1.5平方米,小于2.5平方米
D.大于2.5平方米
评析:这是一道单项选择题,解题的思路是通过已知的图形面积估测出未知的图形面积,考查学生的量感、推理意识和几何直观的发展情况。估测图形面积属于量感的考查;由已知推断未知属于推理意识的考查;感知几何图形的大小及组成元素,建立数与形的联系,计算图形的大小,属于几何直观的考查。
(二)基于思维模式的试题分析
培养学生的数学思维是数学教育的重中之重。数学课堂是培养数学思维的主要场所,思维能力评价对学生思维能力的形成起着重要的作用。从解题思维的方向出发,数学思维可以分为顺向思维和逆向思维两种思维模式。顺向思维是指根据教材知识讲解顺序来思考问题,逆向思维是指通过反向方式思考问题。笔者依据这两种思维模式,对NEAP四年级“测量”试题进行了统计和分析(如表2)。
统计结果表明:从整体上看,NAEP四年级“测量”试题以顺向思维的考查为主,其考查了48次,逆向思維只考查了7次;从试题内容上看,逆向思维大多在测量属性类试题中考查,主要从多角度考查学生对测量属性的理解。下面借助试题2和试题3具体分析NAEP四年级“测量”试题是如何考查学生的思维模式的。
【试题2】(NAEP 2017年)下面哪个测量工具可以测量水的温度?
A.闹钟 B.尺子 C.弹簧秤 D.温度计
【试题3】(NAEP 2011年)这张图在测量什么?
A.传送包裹的时间 B.包裹的面积
C.包裹的长度 D.包裹的重量
评析:这两道题是考查测量属性和测量工具的问题。试题2的解题关键是学生要知道水的温度是由特定的测量工具(温度计)测量的,与教材中的知识讲解思路相同,属于顺向思维类试题。试题3的解题关键在于学生要识别出图中的测量工具(秤),且要清楚秤是用来测量物体重量的工具,属于逆向思维试题。
(三)基于问题情境的试题分析
NAEP 2019小学四年级数学评估框架中明确指出,问题情境包括来源于学生熟悉的真实世界的现实情境和来源于数学学科的纯数学情境,要努力寻求现实情境和纯数学情境之间的平衡,从而达到丰富多样的情境与具体数学知识的有机结合[4]。因此,笔者依据以上两种情境,对NAEP四年级“测量”试题的问题情境设置进行了统计与分析(如表3)。
统计结果表明,在所统计的55道试题中,现实情境类试题有35道,占比63.6%;纯数学情境类试题有20道,占比36.4%。为深入探析,现以具体试题为例进行说明。
【试题4】(NAEP 2013年)Kelly正穿着短袖T恤在外面玩,请估计现在外面的温度可能是多少华氏度?(华氏度=32+摄氏度×1.8)
A.0℉ B.32℉ C.85℉ D.212℉
评析:这道题考查学生对温度的感知能力,通过Kelly的穿着推测温度的高低,选择比较合理的温度。该题以身穿短袖T恤的Kelly在室外玩耍为背景,符合学生的认知水平,属于现实情境的考查。把感知温度放到现实情境中考查,使学生在解决问题的同时,加深对温度高低的理解,提高推理意识。
(四)基于表征方式的试题分析
试题的表征方式影响学生读取试题信息的准确性以及选择解题策略的难易程度。因此,表征方式成为命题中不可忽视的影响因素。数学表征方式分为口头表征、符号表征、图表表征、多元表征(使用了两种或三种表征形式的组合)四种[5]。笔者依据以上的分类方式,对NAEP四年级“测量”试题进行了统计和分析(如表4)。
统计结果表明,在55道试题中,用多元表征方式考查的次数最多,为24次,约占43.6%;没有用符号表征考查的试题;用口头表征方式考查的次数为18次,约占32.8%;用图表表征方式考查的次数为13次,约占23.6%。现以具体试题进行深入分析,探究NAEP四年级“测量”试题是如何呈现的。
【试题5】(NAEP 2022年)Talat有一个罐子,他提出了三个和罐子有关的问题,下面哪个测量属性可以回答Talat的问题,请把答案拖至对应的问题上。
【试题6】(NAEP 2011年)一本书的长度单位可能是什么?
A.厘米 B.米 C.平方厘米 D.平方米
评析:这两道试题都在考查学生对测量工具、测量属性及测量单位之间对应关系的判断。不同的是,试题5是以具体的现实情境+图表的形式呈现,属于多元表征;试题6是以纯文字形式呈现,要求学生根据问题的文字表述,找到相应的答案,属于口头表征。
三、思考与启示
“测量”知识与生活应用息息相关,也是当今数学学科教材研究的焦点之一[6]。测量与日常生活、生产劳动以及科学研究有著密切的关系,能够认识测量以及掌握测量的方法应该是每个公民必备的素养之一[7]。基于NAEP四年级“测量”试题的分析,结合《课程标准》的目标要求,笔者得出以下几点启示,为“测量”试题的编制提供参考。
(一)量感和其他素养协同考查,体现综合性
《课程标准》在“命题原则”中明确指出,要坚持素养立意,凸显育人导向。以核心素养为导向的考试命题,要关注数学的本质,关注通性通法,综合考查“四基”“四能”与核心素养。一道试题中包含多个核心素养表现,有利于考查学生各个核心素养表现的发展情况,促进学生的全面发展。同时,也要注意,编制试题时,不应过分追求一道题中要考查的核心素养表现的个数,也不能刻意提高试题难度,增加学生的考试负担。因此,未来我国编制“测量”试题时,需要关注各核心素养表现之间的关联,合理安排核心素养表现的个数和难度水平,提高编制“测量”试题的水平。
(二)试题贴近学生生活,体现应用性
NAEP评估项目命题的特点之一是注重试题情境的真实性。将试题情境与学生实际生活联系起来,有利于学生感受生活中的数学,体会数学的魅力,学会用数学思维思考问题。因此,“测量”试题的编制应该符合学生的认知规律,创设合适的真实情境,设计有意义的问题,促进学生对情境中的问题进行探究与思考。同时,“测量”试题的编制还要注重开放性,避免死记硬背的问题,在学生解题的过程中培养他们的创新意识。
(三)加强逆向思维考查,体现发展性
逆向思维是小学高年级学生在数学学习过程中逐渐形成的数学素养,也是学生学习数学知识所必须具备的能力[8]。逆向思维不仅可以帮助学生破除定向思维,培养多元思维习惯,还有助于学生提高创新意识,多角度解决数学问题。因此,“测量”试题的编制应该从多角度考查学生的测量素养和能力。同时,“测量”试题的编制还应创新解题模式,除了传统的填空题、计算题、应用问题,还可以借助信息技术,采用拖拽、连线、实践操作等形式考查学生的测量素养。
(四)优化表征方式,体现过程性
丰富的信息载体和多元化的表征方式有利于改善学生的作答感受,增添试题的趣味性,激发学生的思考能力,评价学生的实际水平。借助不同的表征方式,可以使试题更加灵活,从而增强试题的深度和广度。采用多元表征的形式呈现试题时,试题的文字表达要简洁,避免不必要的表达语句,且图表和故事背景需符合学生的认知水平和生活经验,以体现数学的文化价值。因此,未来我国编制“测量”试题要重视试题的表征方式,有效发挥试题的测评作用。
参考文献:
[1]许添舒,臧悦,孔企平.小学数学“测量”课程国际改革动向分析[J].小学数学教师,2018(4):76-78.
[2]中华人民共和国教育部.义务教育数学课程标准(2022年版)[M].北京:北京师范大学出版社,2022.
[3]王利庆.一道几何参赛试题的编制、品析及感悟[J].中学数学杂志,2021(6):48-50.
[4]阿斯亚·图尔荪,王利,杨新荣.NAEP2019小学数学评估框架及试题特点分析[J].小学数学教育,2022(21):4-6.
[5]沈阳,张晋宇,鲍建生.表征在数学教育中的研究现状[J].数学教育学报,2022,31(2):82-89.
[6]丁梦佳. 中美韩小学数学教材“测量”内容比较研究:以人教版、加州版、科创版为例[D].青岛:青岛大学,2020.
[7]何学冬. 中新两国小学数学“测量”内容的比较研究[D].重庆:西南大学,2020.
[8]刘红红.逆向思维在小学高年级数学解题中的应用策略[J].智力,2021(19):77-78.
(江西科技师范大学数学与计算机科学学院)
