课程思政视阈下微课教学设计实践探索

严静　姜兆敏

摘 要：微课易于学生聚焦教学的重难点，便于学生的自主学习.本文以融入思政元素的“求曲面的面积”的微课设计为例，将高等数学课程与思政紧密结合，既提高了教学效果，又培养了学生的优良品质.

關键词：课程思政；微课；曲面面积；教学设计

1 研究背景与意义

1.1 微课引入高等数学课程的必要性

近几年来，由于疫情的原因，教师不得不利用直播、录播、慕课、微课等线上教学方式进行教学工作.相比其他线上教学方式，微课具有如下特点［1］：一、 时间短但内容精.微课的时长一般约为10—15分钟，甚至更短，主要结合动画、公式、图片、文字等多种形式，把一个或多个知识点完整地用视频的形式呈现出来；二、 方式灵活多样.学生不受时间、空间的限制，可以借助手机、电脑等设备随时随地进行学习.高等数学是高校理工科学生的公共基础必修课，不仅是其他数学课程和许多专业课的基础，而且在实际生活和科研领域都有着极其重要的作用，但该课程中许多概念抽象、内容逻辑性强，计算复杂，再加上高等数学一般都是大班授课，教师利用传统的授课方式会让学生感到枯燥乏味，从而影响教学效果.如果教师根据知识点制作相应的微课视频，学生就可以根据自身的情况选取自己薄弱点利用课后时间反复学习，能够有效提升学习效果.因此，将微课引入高等数学教学中，充分发挥微课优势是十分必要的.当然，要吸引学生观看微课视频，教师必须精心选取课程内容，更要花大量的时间和精力来设计和制作微课.

1.2 课程思政与高等数学相结合的重要性

2020年5月28日，教育部印发《高等学校课程思政建设指导纲要》，指出全面推进课程思政建设是落实立德树人根本任务的战略举措.高等数学是理工科学生在大学一年级最重要的课程之一.大一新生的人生观和价值观尚不成熟，面对世界深刻复杂的变化、信息时代各种思潮的相互激荡，面对学业、情感等多方面的考量，他们容易丧失理想信念，迷失生活方向.因此，大一新生的成长需要高等数学充分发挥其课程思政功能.近年来，高等数学教学中如何渗透课程思政已引起高校数学教学的重视与思考［2］.许多一线教师、专家学者探讨了课程思政具体的实施途径［3］［4］，主要包括数学史、数学文化的融入，数学在实际生活或科学领域中的应用案例，挖掘数学中蕴含的唯物辩证法、方法论等.思政元素的融入不仅有助于学生深刻理解数学概念、理念和思想，形成数学知识的体系化、系统化，提升学生探索、创新和实践的能力，而且有助于学生提高学习数学的兴趣和自信心，养成良好的学习习惯，树立积极进取、奋发向上的拼搏精神和严谨求实、善于思考、钻研的科学精神，建立乐观、优质的思想品质［5］.

基于以上背景，本文着重探讨高等数学中“二重积分的几何应用——求曲面的面积”的微课设计.

2 “二重积分的几何应用——求曲面的面积”教学设计

曲面面积在高等数学中既是重点也是难点，因为曲面积分既是二重积分的一个重要的几何应用，也是第一类曲面积分计算的基础.

2.1 教学分析

本节课的教学内容为利用二重积分计算曲面的面积.教学目标可细分为知识目标、能力目标和情感目标.其中知识目标为理解元素法推导曲面面积公式，掌握公式的应用；能力目标是培养学生逻辑推理、空间想象、数学应用等能力；情感目标为提高学生的数学学习兴趣，培养学生正确的价值取向，激发学生的爱国意识.教学重点一是曲面面积公式的推导，二是面积公式的应用.教学难点是曲面面积元素的确定.学情方面，学生对元素法已经有了一定的了解并已熟练掌握二重积分的计算;另外，作为网络原住民，当代大学生课堂集中注意力时间短，利用手机、电脑等电子设备进行智能化、碎片化学习已经成为他们获取知识的常用方式.

2.2 教学设计思路和思政切入点简介

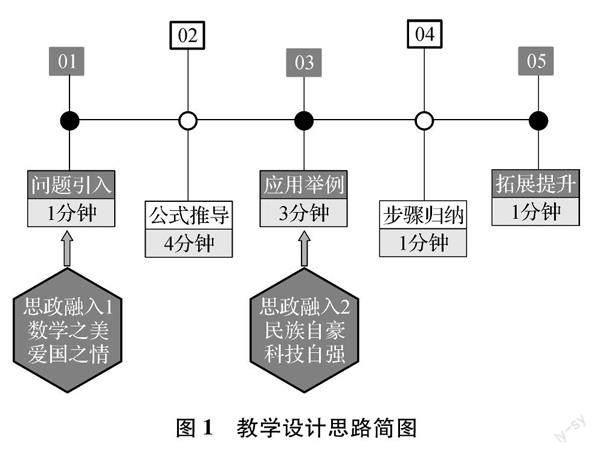
本着知识、能力、情感的有机融合，教学设计思路及思政切入点如图1所示.首先通过生活中的常见曲面引入问题：曲面的面积应用广泛，如何计算曲面的面积呢？为激发学生的兴趣，特别提出如何计算“中国天眼”的接收面积，课件中展示相关图片并对“天眼”及其创始人南仁东作简要介绍，让学生感受到数学之美，引发他们的爱国之情.接着用元素法进行面积公式的推导，得到公式之后，作为应用举例，解决一开始提出的“天眼”面积问题，利用计算的结果，再将“天眼”与美国的阿雷西博望远镜进行比较，能增强学生的民族自豪感和科技自强的使命担当.通过解决问题的过程，归纳出曲面面积的计算步骤，最后提出两个探究性的问题，拓展学生的数学思维，培养学生举一反三的能力，提升学生深入思考和自主学习的能力.

2.3 教学过程的设计

2.3.1 创设情境 案例引入

从日常生活入手，课件展示许多家居用品，著名建筑，都是曲面的造型.同时指出在设计它们时不仅要考虑美观，还要考虑功能、材料、成本等因素，很多都涉及到面积的计算，特别是曲面的面积，由此引入曲面面积的计算问题.特别引入一个具体案例：举世闻名的“中国天眼”——一个有着500米口径的球面射电望远镜（见图2），中国天眼是目前世界上最大最灵敏的单口径射电望远镜，那么它的接收面积也就是内表面积究竟有多大呢？这个问题能调动学生探究、求解问题的欲望.在该案例中同时介绍“天眼”创始人南仁东，我国杰出的天文学家，他放弃了高于国内300倍的薪酬，毅然选择回国，带领科研团队克服重重困难，历经22年才完成了这项伟大的工程.

此环节不仅是课程的引入，也是思政的融入之一，学生能感受到数学在实际生活中的应用广泛，数学与建筑之美的融合；科学家不畏艰难，无私奉献的爱国主义精神.

2.3.2 微元思想 公式推导

假设空间一张光滑曲面，方程为z=f（x，y），它在xOy面上的投影区域为D，现在要求曲面的面积.

通过前期的学习，我们知道对于不规则的物体，通常可以利用极限思想将它转化为积分来求解，也就是我们前面介绍过的元素法，其主要步骤为：分割、近似、求和、取极限.在这个问题里面，它的具体方式就是先分割曲面，为了便于分析，我们不妨用平行于坐标面的平面进行分割，这样分割之后，我们看到，每一片小曲面的面积在它的局部就可用它的切平面面积来近似代替，也就是“以平代曲”，并且分割越细，这些小切平面的面积之和就越接近整片曲面面积（见图3）.将它们求和取极限就能得到积分表达式.在整个过程中，最关键也是最困难的是如何求小切平面的面积.

我们取其中有代表性的一小片切平面来分析，它的面积也就是曲面的面积元素dS.由于分割曲面的都是平行于坐标面的平面，所以这个小切平面以及它的投影区域都是矩形，投影区域面积dσ也等于dxdy.为了便于找出dS和dσ的关系，我们将这个小切平面向下平移，平移到和它投影区域的一条边贴合在一起（此处课件展示为动画）.将它们放大来看，如图4，假设两平面的夹角为γ，这为了更形象地说明天眼接收面积之大，作出如下比较：一个标准足球场的面积为7140平方米，它比35个标准足球场的面积还要大.在天眼建成之前，美国的阿雷西博曾是世界上最大的射电望远镜（课件展示相关图片，与天眼作出比较），它的口径为305米，接收面积约73000平方米，不足中国天眼的三分之一，并且由于多年老化和维护不利，阿雷西博已于20年发生坍塌而废弃，退出了历史的舞台.“中国天眼”已经取代了阿雷西博的地位，无论从精密程度还是综合性能，都远远超过了阿雷西博.此处思政的融入明显能够提升学生的民族自豪感和爱国主义精神，培养学生勇于创新的科学精神，积极投身国家重大工程建设的历史使命感.

2.3.4 步骤归纳 突出重点

回顾刚才的整个解题过程，归纳曲面面积计算的四个步骤：建方程、定投影、求偏导、算积分.其中最重要的是建方程和定投影，如果条件已给出曲面的方程，那么只要找到这个方程并将它表示成显函数z=f（x，y）的形式；确定投影时，要充分发挥我们的空间想象力，有时还需要借助曲面的交线在坐标面上的投影.

3 教学总结

本次微课时长约10分钟，整体上以“提出问题—分析问题—解决问题”为脉络主线，首尾呼应，体现了知识的完整性.教学设计符合学生的认知规律和学习程度要求，教学过程以知识传授、价值引领、能力培养相结合，能达到较好的教学效果.作者就所授课班级采用课堂结合微课视频讲解了这部分知识点，调查显示极大提高了学生学习兴趣和学习热情，加深了学生对“元素法”思想的理解，并能较快掌握曲面面积公式的应用.本微课不仅得到了学生的认可，还得到了高校同行的肯定，2022年12月，作者凭借微课《二重积分的几何应用——求曲面的面积》荣获江苏省高校第八届数学基础课青年教师授课竞赛暨第二届全国大学数学课程思政邀请赛二等奖.

参考文献：

［1］ 毕金钵.浅谈高等数学翻转课堂微课的内容设计——以“方向导数与梯度的背景”为例［J］.数学学习与研究，2017（14）：2.

［2］ 吴慧卓.高等数学教学中渗透课程思政的探索与思考［J］.大学数学，2019，35（5）：4043.

［3］ 秦厚荣，徐海蓉.大学数学课程思政的“触点”和教学体系建设［J］.中国大学教学，2019（9）：6164.

［4］ 彭双阶，徐章韬.大学数学课程思政的课堂教学实现［J］.中国大学教学，2020（12）：2730.

［5］ 田金凤.高等数学教学中课程思政的教学实施——以《定积分的概念》为例［J］.高等数学研究，2022，25（6）：8790.

基金項目：江苏理工学院校教改项目1：基于GeoGebra的高等数学可视化教学探索（项目编号：11611212120）；江苏理工学院校教改项目2：数学师范生信息技术应用能力的培养与实践（项目编号：11611212123）；江苏省高校大学生劳动教育基础课程群课题：高等数学教学中思政案例设计与应用实践研究（课题编号：2021JDKT050）.