基于GeoGebra剖析空间角的概念
2023-07-10姜林蔡华
姜林 蔡华

摘 要:在空间角(异面直线所成的角、直线与平面所成角、二面角的平面角)的教学中,教师往往花费较多的时间设计概念的引入,但缺少剖析概念的环节,以至于学生在解题时,存在“主观臆断、无中生有”等“无目的”的解答现象.因此,本研究以GeoGebra为平台对空间角的概念做进一步的剖析,重构空间角的概念,使其与学生解题过程保持一致,加深学生对空间角的理解,为教师教学提供一定的参考.
关键词:GeoGebra;空间角;概念剖析
1 问题提出
学生理解数学概念是解决数学问题的前提.在“以教师为主导”的传统教学模式下,教师只能借助或不借助实物模型对异面直线所成的角、直线与平面所成角、二面角的平面角的概念进行教学,大部分是采用直接呈现概念,紧接着例题讲解与学生练习的教学方式.然而随着“以学生为主体”的教学理念的提出,教育信息化的发展,使用信息技术辅助教学是必然的趋势,并且课程标准指出“可以使用信息技术展示空间图形,为理解和掌握图形几何性质提供直观”[1].
教师也逐渐使用信息技术辅助空间角的教学,然而针对空间角的概念教学多为教学设计和教学反思[2].尽管教师花费较多时间引导学生自主构建空间角的概念[3],但是很少使用信息技术对空间角的概念进行剖析,缺少从概念归纳解题方法的教学环节,以至于学生在自主解答问题时抓不住要点,使得空间角的概念与实际解题出现一定的脱节.我国数学教育家张景中院士[4]提出了教育数学的三条原理“数学教育应当从学生脑海中找概念、从概念中产生方法、由方法形成模式”,因此,要让学生能够理解空间角的概念并解决相关问题,那么对空间角的概念进行剖析就显得尤为重要.
本研究将从剖析概念的必要性入手,并以GeoGebra为平台对空间角进行逐一剖析,重构与解题过程保持一致的“新”概念,归纳解题方法并应用,最后提出GeoGebra辅助立体几何教学的使用建议.
2 GeoGebra辅助教学的优势
尽管教师能够使用信息技術辅助教学,但是空间角对学生的直观想象能力有着较高的要求,那么使用恰当的教学软件就能实现事半功倍的教学效果[5].GeoGebra是一款免费开源的数学教学软件,具有3D空间直观的绘图区域、代数运算、几何平面、统计概念等强大的功能,其3D绘图功能在立体几何教学中有着较大的优势[6].
2.1 3D绘图区
3D绘图区域主要由一个平面和空间直角坐标系构成,为在此区域构建几何对象提供了直接的构建平台,如图1所示.并且使用鼠标或者教室一体机的接触笔能改变观察的视角,实现从多角度观察几何对象.
2.2 工具便捷性
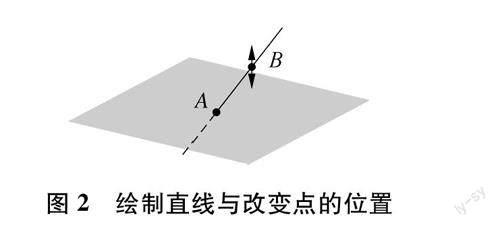
立体几何作图是传统教学方式最耗时的环节,教师在教学和解题过程中都需要花较长的时间在黑板上进行作图.3D作图的工具,可以实现快速作图.比如,使用直线工具,根据两点确定一条直线就能够在平面上绘制一条直线AB,如果想让直线AB不在平面内,可以点击其中一个点B,当出现上下两个箭头时,就可以实现点的上下平移,如图2所示;当出现四个箭头时,可以实现点的前后左右平移.此外,常见的工具还有,平面工具(三点确定一个平面)、正六面体、棱锥、棱锥、圆锥、圆锥以及平移、旋转、轴对称等变换工具.
在具有较强空间感和作图便捷性的3D绘图区,完全实现异面直线所成角、直线与平面所成角、二面角的平面角与GeoGebra的融合,体现该软件在数学概念教学中的优势.
3 空间角的概念剖析与重构
空间角是指高中数学学习内容中的异面直线所成角、直线与平面所成角以及二面角的平面角.以“普通高中教科书数学必修第二册”中的空间角为剖析对象.
3.1 异面直线所成角
异面直线所成角的概念:已知两条异面直线a、b,经过空间中任意一点O分别作直线a′//a,b′//b,把直线a′与b′所成的角叫做异面直线a与b所成的角(或夹角).
从概念中可以发现几个关键短语“任意一点、分别作直线”,但是这与例题的解答过程有差异.以教材的第147页的例1为例,找出其中的差异.
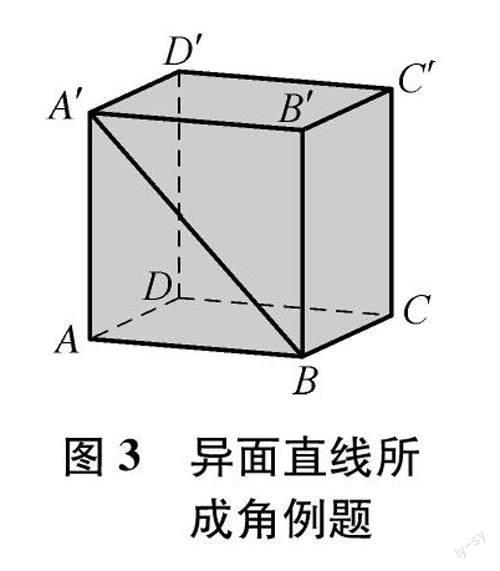
问题1:如图3所示,在正方体ABCD-A′B′C′D′中,求直线BA′与CC′所成的角的大小.
解法:∵ABCD-A′B′C′D′是正方体,
∴BB′//CC′,
因此∠A′BB′为直线BA′与CC′所成的角.
∵∠A′BB′=45°,
∴直线BA′与CC′所成的角等于45°.
与异面直线所成角的概念相比,例题的解答过程,并没有“作直线平行”,而是证明直线平行,最后找到角并在三角形中求解角的大小.通过对比可以发现异面直线所成角的概念描述与解答过程存在不一致,为避免学生解答时出现“主观臆断”,让学生有解决问题的方向,就需要对概念进行剖析.
使用GeoGebra绘制异面直线a、b,在使用“描点”工具,绘制“任意点O”;显然,空间中过点O的直线有无数条,但是经过点O并且与直线a平行的直线只有一条a′;同理,经过点O并且与直线b平行的直线也只有一条b′;因此,只需要分别证明过点O的直线a′、b′平行于直线a或者直线b,那么直线a′、b′所成的角就是异面直线a、b所成的角.
综上,可以得出异面直线所成角的另一种描述:已知两条异面直线a、b,若能证明经过空间中任意一点O的直线a′、b′分别平行于直线a、b,那么直线a′与b′所成的角叫做异面直线a与b所成的角.(当点O在直线a或直线b上时,仅需证明一次直线平行)
3.2 直线与平面所成角
直线与平面所成角:一条直线l与一个平面α相交,但不与这个平面垂直,这条直线叫做这样平面的斜线,斜线和平面的交点A叫做斜足.过斜线上除斜足外的一点P向平面α引垂线PO,过垂足O和斜足A的直线AO叫做斜线在这个平面上的射影.平面的一条斜线和它在平面上的射影所成的角,叫做这条直线和这个平面所成的角.
概念中的关键点是“过点P向平面α引垂线PO”,其含义是“过点P作平面α的垂线PO”,但是实际问题的解答却不是“作垂线”,而是“证明垂直”.对教材第152页的例4进行分析,对比例题的解答过程与概念之间的差异.
问题2:如图5所示,在正方体ABCD-A1B1C1D1中,求直线A1B和平面A1DCB1所成的角.
解:连接BC1,B1C,BC1与B1C相交于点O,连接A1O.
设正方体的棱长为a.
∵A1B1⊥B1C1,A1B1⊥B1B,B1C1∩B1B=B1,
∴A1B1⊥平面BCC1B1,即A1B1⊥BC1,
∵BC1⊥B1C,
∴BC1⊥平面A1DCB1,
即A1O为斜线A1B在平面A1DCB1上的射影,∠BA1O为A1B和平面A1DCB1所成的角.
在Rt△A1BO中,∵A1B=√2a,BO=(√2/2)a,∴BO=(1/2)A1B,即∠BA1O=30°,故直线A1B和平面A1DCB1所成的角为30°.
分析解答过程可以发现,在解题过程中,并没有“作平面的垂线”这样的步骤,这就是解答过程与概念不一致的地方.因此为了概念与解答过程保持一致,让学生能够深刻理解直线与平面所成的角,并在解题过程中有一定的思考方向,就需要对概念进行剖析,以便学生能掌握知识.
使用GeoGebra绘制平面α、斜线AP,点P是除斜足A以外的任意一点,显然在空间中过点P的直线有无数条,然而垂直于平面α的直线只有一条PO,即可以证明过点P的直线PO垂直于平面α,垂足为O,最后使用GeoGebra的“直线”工具和“角度”工具,分别绘制射影和直线与平面所成的角β,如图6所示.
综上所述,直线与平面所成角的另一种描述:已知斜线l、平面α,斜足为点A,在斜线l上的任意一点P(除斜足外),若能证明过点P的直线垂直于平面α,垂足为点O,那么射影AO与斜线AP所成的角β就是直线l与平面α所成的角.(实际问题中,任意一点往往是确定斜线的两点之一)
3.3 二面角的平面角
二面角的平面角概念:在二面角α-l-β的棱l上任取一点O,以点O为垂足,在半平面α和β内分别作垂直于棱l的射线OA和OB,则射线OA和射线OB构成的∠AOB叫做二面角的平面角.
從三个空间角的概念的描述可以发现它们的共性都是“作出”具有平行或垂直关系的直线,把握它们之间的共性,使教学具有连贯性[7].因此根据前文的剖析,通过类比就可以得到二面角的平面角的另一种描述:在二面角α-l-β的棱l上任取一点O,在半平面α和β内分别有两条射线OA和OB都经过点O,若能证明射线OA和OB都垂直于棱l,则射线OA和射线OB构成的∠AOB叫做二面角的平面角.
这样的概念描述让数学概念与解题过程保持一致,对学生理解概念和解题都有很大的帮助,并为学生提供了清晰的解题思路,减少出现“主观臆断、无中生有”的解答现象,让学生在解题时具有明确的目的.
4 解题方法的归纳与应用
4.1 类比归纳解题方法
有效的概念重构能够促进学生对概念的理解[8],而恰当的教学软件能够实现事半功倍的教学效果[9].通过使用GeoGebra软件对空间角的概念进行剖析,并得到符合学生解题思路的“新”概念.而三个空间角的“新”概念中蕴含着解决空间角相关问题的一般性步骤:(1) 找点;(2) 进行证明;(3) 确定角;(4) 在三角形中求角.概念的剖析使学生有了解题的思路,避免出现“主观臆断、无中生有”的错因,也在解题过程中进一步理解相关概念.
4.2 “新”概念的应用
结合具体的问题,说明“新”概念与解题过程的一致性.异面直线所成角重构后的概念描述:已知两条异面直线a、b,若能证明经过空间中任意一点O的直线a′、b′分别平行于直线a、b,那么直线a′与b′所成的角叫做异面直线a与b所成的角.(当点O在直线a或直线b上时,仅需证明一次直线平行)
问题3:如图7所示,在正方形ABCD-A1B1C1D1中,O1为底面A1B1C1D1的中点,求证AO1⊥BD.
结合概念分析问题:题目的要求是证明异面直线AO1与BD垂直.若可以求出AO1与BD所成角的大小为90°,那么就说明AO1⊥BD.
根据解题方法:
(1) 找点(教学过程中教师可以引导学生逐一找点A、B、D、O1观察分析哪个点比较合适,可以发现比较恰当的点是O1)
(2) 进行证明(由于点O1在直线AO1上,要证明过点O1的直线平行于BD,那么就需要作辅助线B1D1);
(3) 确定角(异面直线所成的角就是∠AO1B1);
(4) 在三角形中求角(构造△AB1D1,根据题意知道△AB1D1是等边三角形,AO1是中线,即可以求得∠AO1B1=90°).如图8所示.
5 结束语
通过借助GeoGebra软件对空间角的概念进行剖析,结合相应的例题和类比方法,重构了空间角的概念,让绝大部分学生能够较轻松地理解概念并能解决相关的问题.归纳一般性的解题步骤:(1) 找点;(2) 进行证明;(3) 确定角;(4) 在三角形中求角.此外,要使学生理解数学概念、法则、公式、定理,并能够掌握运用,那么对其的剖析环节必不可少.而在立体几何内容的教学过程中使用GeoGebra辅助教学,不仅有助于学生深刻理解数学知识,提升直观想象能力和学习数学的兴趣,而且对培养学生数学思维也有较大的帮助.
参考文献:
[1] 中华人民共和国教育部.普通高中数学课程标准(2017年版)[S].北京:人民教育出版社,2020:2530.
[2] 张林森,黄华.概念教学 自然为贵——“异面直线所成的角”教学设计、实践与评析[J].中国数学教育,2017(18):435.
[3] 曾盛,邢晓丹.简约而不简单的数学本真课堂教学——观数学公开课“异面直线所成的角”后的教学思考[J].上海中学数学,2017(9):435.
[4] 张景中.直来直去的微积分[M].科学出版社,2010.
[5] 张志勇.高中数学可视化教学:原则、途径与策略——基于GeoGebra平台[J].数学通报,2018,57(7):214+8.
[6] 谭媛媛.基于GeoGebra的问题驱动式课堂教学实践——以三视图教学为例[J].中国现代教育装备,2022(14):525.
[7] 俞廉洁,杨元韡.以“异面直线所成角”的教学设计为例谈立体几何的概念教学[J].中学数学月刊,2021(8):435.
[8] 朱建平,袁卫刚.“异面直线所成角”课堂教学的反思与重构[J].中学教学参考,2020(2):67.
[9] 左晓明,田艳丽,贠超.基于GeoGebra的数学教学全过程优化研究[J].数学教育学报,2010,19(1):99102.
