潜艇声诱饵防御声自导鱼雷改进PSO 算法

侯文姝,陆铭华

(海军潜艇学院,山东 青岛,266199)

0 引言

潜艇使用自航式声诱饵对抗声自导鱼雷主要在于迅速抉择对抗方案,确定潜艇机动规避的时机、潜艇转向角、航速、声诱饵发射时机、一次转向角、变深航深和二次转向角等参数,从而达到使鱼雷与潜艇距离最大的优化目标。几何分析[1]、解析模型[2]、并行算法[3-4]以及遗传算法[5-7]等方法被用于求解该类问题。孟庆玉等[8]指出如果目标随机机动或鱼雷非直航搜索,由于鱼雷和目标相互运动的确定性,使得应用解析法比较困难。采用大规模并行算法则对硬件要求比较高,在潜艇上实现难度较大。

粒子群优化(particle swarm optimization,PSO)[9]算法是计算智能领域除了蚁群算法、鱼群算法之外的一种群体智能算法[10]。在此基础上开展的研究也有很多,如Shi 等[11]提出动态调整惯性权重策略对其进行改进,Wang 等[12]引入收缩因子,Niu 等[13]采用自适应学习策略等。

对于潜艇使用单个小口径自航式声诱饵防御正在进行蛇形搜索声自导鱼雷,使鱼雷与潜艇距离最大的问题,采用基于并行计算的改进PSO 算法进行优化。首先通过分别改变种群粒子数、迭代次数和粒子速度的上限以及加速度因子等参数和种群初始化方法,研究这些因素对并行计算PSO算法的影响,然后进行算法改进,使得算法在不增加计算量的情况下得到更快收敛。

1 模型建立和PSO 算法

在三维空间中,当潜艇接收到鱼雷报警信号时,声自导鱼雷正在采用主被动联合自导进行蛇行搜索,发现潜艇或诱饵后立即进行尾追机动跟踪。对声诱饵进行尾追跟踪时,一旦潜艇进入鱼雷对潜艇的开始识别距离且在鱼雷主被动声自导探测范围内,鱼雷弃声诱饵改为尾追潜艇。鱼雷一旦丢失声诱饵或与声诱饵接近到一定距离时,识别出诱饵为假目标,鱼雷进行环形机动搜索潜艇[14]。若环形机动一圈后未搜索到潜艇,则继续进行蛇形机动搜索潜艇。

传播损失TL采用Baker 给出的表面声道经验公式计算[15];海洋环境噪声NL服从Kundson 谱[15];潜艇反射强度TS随信号入射方向的变化规律可以近似表示为蝶形[8];潜艇辐射噪声强度采用经验公式[8]计算。由于声诱饵尾部存在盲区[5],如果目标和诱饵同时进入鱼雷的自导作用范围,则鱼雷优先跟踪目标[5]。鱼雷的主被动声自导能否发现目标采用基于声呐方程的鱼雷主动检测模型和被动检测模型[7-8]进行判别。鱼雷接收频段内的鱼雷自噪声随深度变化[8]。

基于并行计算的PSO 算法适应度值取潜艇声诱饵防御鱼雷仿真结束时潜艇与鱼雷的距离d,采用四线程并行计算方法对一次迭代过程中的多个粒子适应度值进行计算。设D(D=7)维空间中,由n个粒子组成的种群为P=(P1,P2,···,Pn),第i个粒子为向量Pi=(t1,α1,z1,t2,α2,z2,α3)iT,代表第i个粒子在D维搜索空间中的位置,也代表问题的一个潜在解[10],其中:t1为潜艇机动规避的时机;α1为潜艇转向角;z1为潜艇变深航深;t2为声诱饵发射时机;α2和 α3为声诱饵一次和二次转向角;z2为声诱饵变深航深。参数取值范围:t1,t2∈[0,tend],z1,z2∈[10,300],α1∈(-180,180],α2,α3∈[-90,90],粒子位置被限制的区间记为[Pmin,Pmax]。转向角为0 表示不变向,小于0 表示左转,大于0 表示右转,所有参数取整。第i个粒子的速度为Vi=(V1i,V2i,V3i,V4i,V5i,V6i,V7i)T,速度被限制的区间为[-Vmax,Vmax]。粒子和速度初始化是通过生成取值范围内的随机数取整得到的。第k+1 次迭代中粒子速度更新和位置更新分别为[10]

式中:c1和c2为加速度因子,为非负的常数;r1和r2为分布在[0,1]区间内的随机数[10];个体极值是第i个粒子计算出的最优适应度值所对应的粒子位置;群体极值Pgbest是种群中所有粒子搜索到的适应度最优位置[10]。

2 参数和种群初始化方法对优化结果的影响

假设潜艇航向为90°,航深为80 m;鱼雷报警舷角右舷140°,航向为40°,航深为40 m。时长tend=7 min,仿真间隔dt=0.1 s。

粒子群迭代次数50 次,种群粒子数为60 个,粒子群加速度因子c1和c2均取值为1,粒子速度的上限Vmax=[10,6,20,10,20,10,20]T,种群初始化采用取随机数的方法,1 次仿真中粒子个体极值的适应度值如图1(a)所示。图1(a)中,有4 个粒子表现比较优异,适应度值大于7 000 m,还有2 个粒子适应度值分别在6 700 m 左右,这些表现优异的粒子大多在第20～40 次迭代过程中收敛。

图1 粒子个体极值适应度值Fig.1 Fitness of individual extreme value of each particle

通过分别改变种群粒子数、迭代次数、粒子速度的上限、加速度因子等参数和种群初始化方法,研究这些因素对算法的影响。粒子个体极值的适应度值如图1(b)～(f)所示。其中,图1(f)采用的种群初始化方法为在一个可行解附近生成粒子的方法,可行解为[10,6,20,10,20,10,20]T,对应的适应度值d=7 348 m。该可行解为图1(a)最后一次迭代群体极值。

分别采用增加种群粒子数(图1(b))、增加迭代次数(图1(c))、改变粒子速度上限的方法(图1(d))使得个体极值适应度值大于7 000 m 的粒子个数也有所增加。加速度因子均取值为2(图1(e))对结果影响不大。种群初始化方法改变(图1(f))后,20 个粒子在第1 次迭代时的个体极值的适应度值大于7 000 m,其他粒子在迭代过程中个体极值的适应度值也能逐步增大,到仿真结束有51 个粒子适应度值大于7 000 m,20 个粒子大于7 500 m。由于种群初始化方法为在一个可行解附近生成粒子,因此所有粒子都是在该可行解附近更新位置,达到了针对该可行解进一步寻优的目的。

对这6 种情况分别进行1 000 次仿真,每一次仿真最后一次迭代群体极值的适应度值分布如图2 所示,平均仿真耗时分别为18.82、39.05、36.16、18.80、18.78 和21.88 s。图2(a)群体极值的适应度值在1 500～7 700 m 范围内,主要分布在1 800、3 800 和7 600 m 左右,这说明在1 000 次仿真中,并不是所有仿真最后一次迭代群体极值适应度值都能达到7 000 m,仍然存在粒子无法寻优至适应度值较大的情况。且根据分布情况可以看出,图2(c)和(d)所示群体极值的适应度值在7 500 m以上的统计次数较多,分别达到741 和785 次,表现比较优秀,图2(b)所示次之,图2(e)最差。图2(f)所示的1 000 次仿真适应度值均大于7 500 m,而且出现40 次仿真适应度值大于7 700 m 的情况。

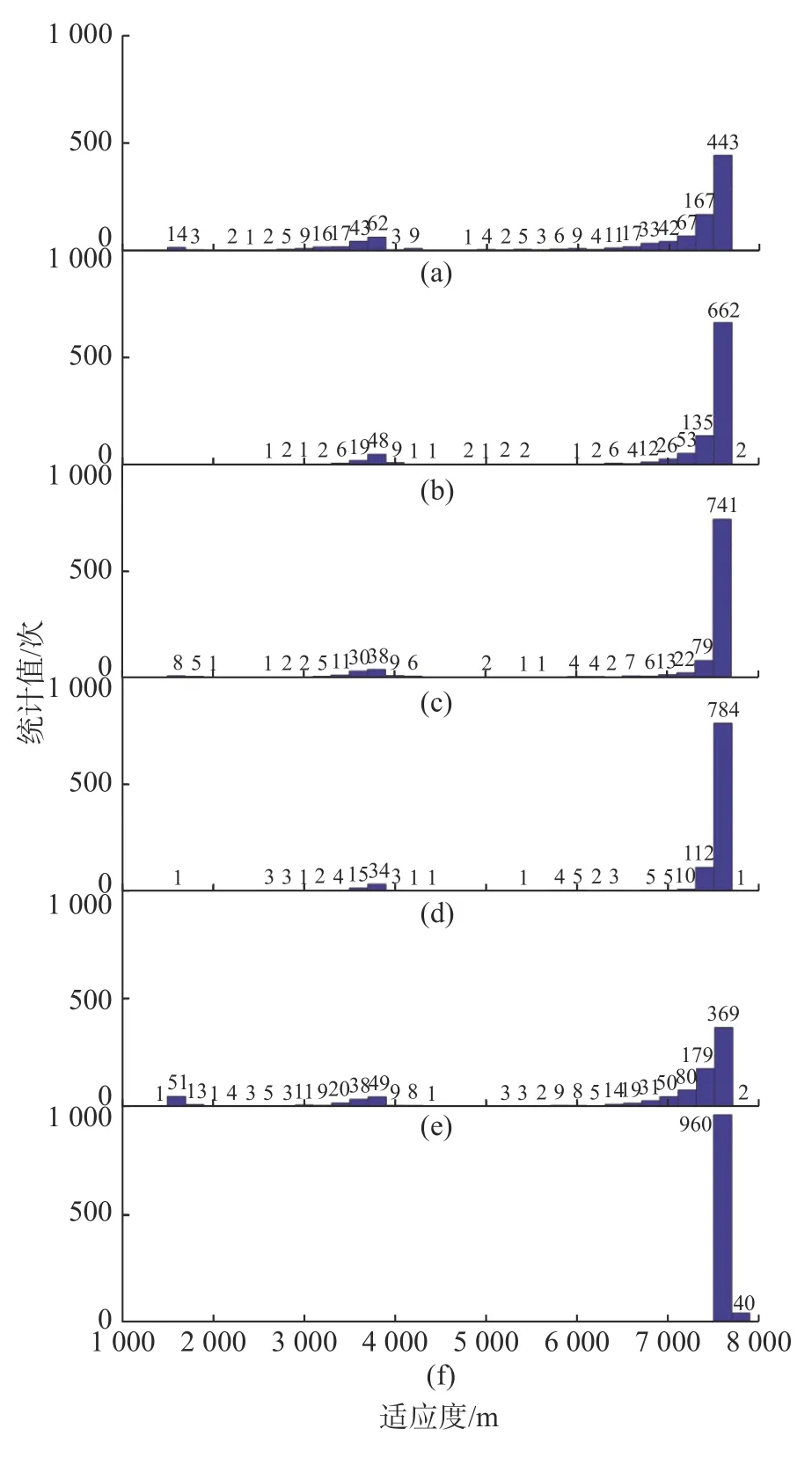
图2 最后一次迭代群体极值适应度值分布Fig.2 Distribution of fitness of swarm extreme value in the last iteration

参数和种群初始化方法的改变对优化结果的影响主要是: 增大加速度因子没有改善结果;增加种群粒子数和迭代次数对仿真结果有一定的改善,但是计算量也相应增加;扩大粒子速度的上限取值对仿真结果改善较大;改变种群初始化方法对仿真结果改善的最大,绝大多数粒子都能获得较大的适应度值,而且适应度值偏高。因此改进的方向主要是: 1) 扩大粒子速度的上限;2) 引入在可行解附近生成粒子群的方法。

3 改进PSO 算法

算法结构改进采用引入在可行解附近生成粒子群的方法时,不能直接采用图1(f)所示在一个可行解附近生成粒子的种群初始化方法,因为该可行解的获取必须建立在一次仿真基础上,其计算量时必须叠加这次仿真,导致仿真耗时增加近一倍。

在粒子群算法流程[10]基础上,选择在迭代过程中获取可行解并在其附近生成粒子群对PSO 算法进行改进,基于四线程并行计算对潜艇声诱饵防御鱼雷数学模型进行寻优的改进PSO 算法流程如图3 所示,改进部分用虚线框表示。在粒子位置被限制的区间内生成随机数并取整获得初始化种群,计算初始化种群的粒子适应度值,并取最大值对应的粒子位置为群体极值。为了在不大幅增加计算量的情况下引入在可行解附近生成粒子群的方法,须在迭代过程中获得可行解。取迭代过程中某一次迭代较优的群体极值为可行解。当群体极值适应度值较大时,群体极值适应度值对应的粒子位置为可行解,随即在群体极值附近生成粒子位置。当群体极值适应度值较小时,随机生成粒子群粒子位置。然后采用式(1)和式(2)粒子速度更新和位置更新,再采用四线程并行计算粒子适应度值,并更新个体极值和群体极值。

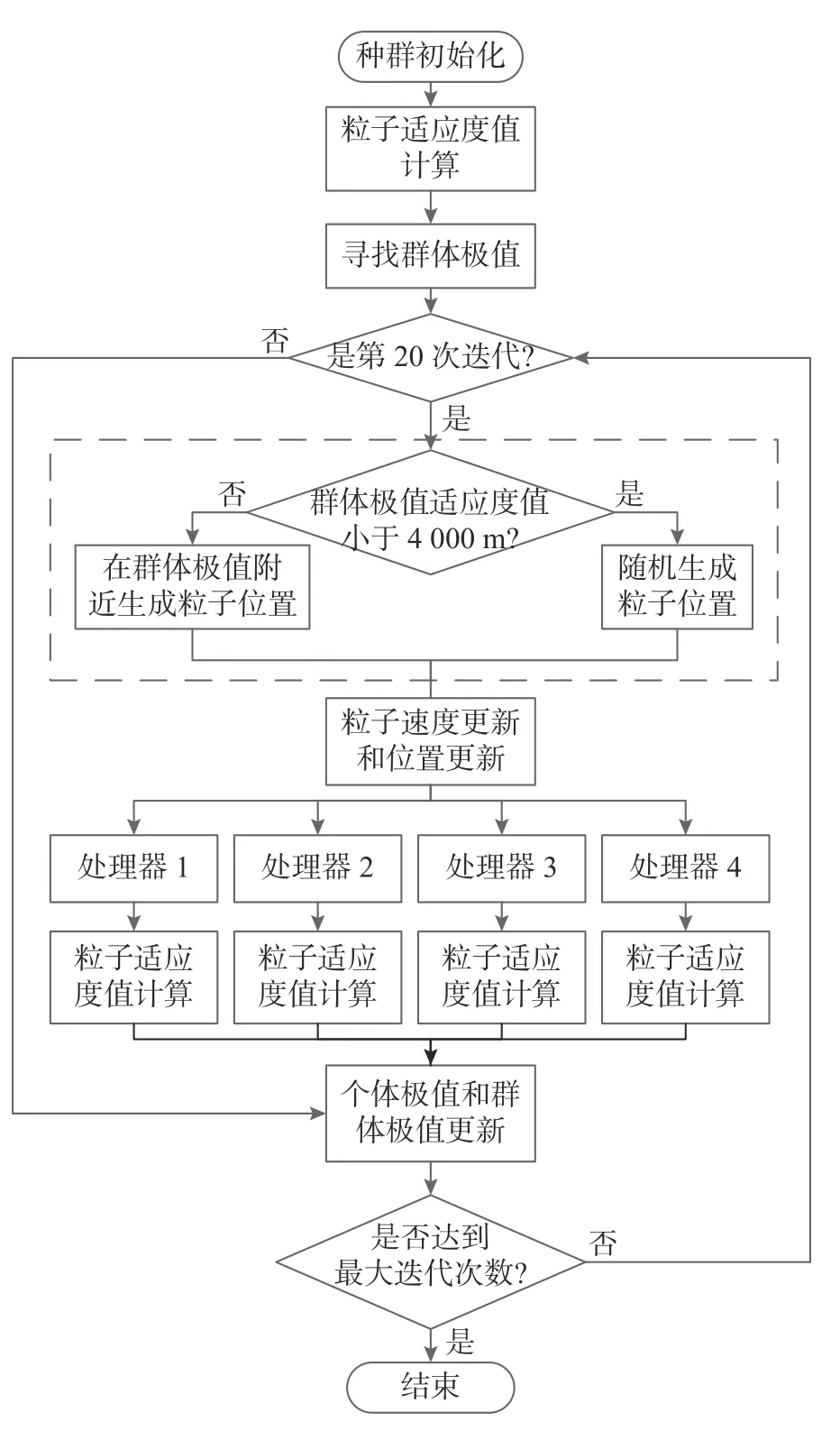
图3 基于并行计算的改进PSO 算法流程Fig.3 Flowchart of improved PSO algorithm based on parallel computation

图3 中,当迭代次数为50 次时,在第20 次迭代开始时根据第19 次迭代群体极值是否超过阈值来选择2 种不同的方法重新生成第19 次迭代所有粒子位置。阈值为4 000 m 是根据图2 统计结果分布情况选取的,当适应度值大于4 000 m 时,适应度值主要分布在7 600 m 左右。粒子群算法改进主要体现在: 第19 次迭代群体极值适应度值大于等于4 000 m 时,在第19 次迭代群体极值附近生成粒子群,小于4 000 m 时,随机生成粒子群,为

取粒子群迭代次数50 次,种群粒子数为60个,粒子群加速度因子c1和c2均取值为1,粒子速度的上限取图1(d)中采用的Vmax=[20,12,40,20,40,20,40]T,仿真耗时20.29 s,最后一次迭代群体极值为Pgbest=[0,71,272,0,-90,10,-71]T,得d=7 647 m,潜艇声诱饵防御鱼雷仿真轨迹如图4 所示。粒子个体极值的适应度值随迭代次数的变化情况如图5 所示,在第20 次迭代时16 个粒子适应度值大于4 000 m,其中有12 个粒子适应度值大于7 000 m,最后一次迭代时,35 个粒子适应度值大于7 000 m,其中15 个粒子适应度值大于7 500 m,该次仿真粒子群总体明显优于图1(a)～(e)的情况。第20 次迭代开始粒子适应度值部分大幅上升,与图1(f)中种群初始化时获得大量适应度值较高粒子的情况相仿,说明在迭代过程中获取可行解并在其附近生成粒子群的方法对PSO 算法进行改进取得成效。

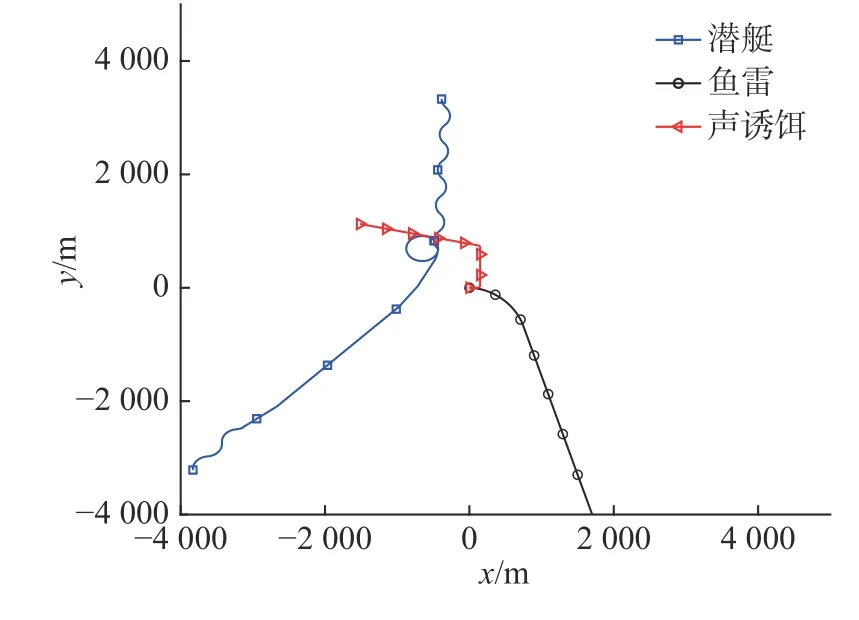
图4 潜艇声诱饵防御鱼雷仿真轨迹Fig.4 Simulation track of defending torpedo by acoustic decoy of submarine

图5 改进PSO 算法的粒子个体极值适应度值Fig.5 Fitness of individual extreme value of each particle of improved PSO algorithm

对改进PSO 算法进行1 000 次仿真,每一次仿真最后一次迭代群体极值的适应度值分布如图6所示,907 次仿真最后一次迭代群体极值的适应度值达到7 000 m 以上,7 500 m 以上的统计次数达到867 次,适应度值大于7 500 m 的仿真次数比改进前(图2(a))提高了95%,高于种群粒子数为120个(图2(c))和扩大粒子速度的上限(图2(d))这2 种情况,接近种群初始化方法为在一个可行解附近生成粒子(图2(f))情况,说明算法得到改善。

图6 改进PSO 算法群体极值适应度值分布Fig.6 Distribution of fitness of swarm extreme value for improved PSO algorithm

4 结论

在潜艇声诱饵防御声自导鱼雷时,为快速得出鱼雷与潜艇距离最大化的防御方案,分析了种群粒子数、迭代次数、粒子速度的上限、加速度因子和种群初始化方法等因素对基于并行计算的PSO算法的影响,确定了算法的改进方向主要有: 1) 扩大粒子速度的上限;2) 引入在可行解附近生成粒子的方法。改进PSO 算法借鉴了在可行解附近生成粒子的方法,在迭代过程中重新生成粒子群。这种方法改善了算法的收敛情况,适应度值大于7 500 m 的仿真次数比改进前提高了95%,且没有增加计算量,收敛得更快,能够提升解算效率。

该算法存在的问题是粒子群的多样性仍受到一定的影响,下一步可以通过增加可行解数量的方法改进种群多样性的问题。