基于小波变换的扩散焊超声C图像融合算法

常 青, 杨程伟, 罗彬杰, 李细峰

(1.华东理工大学 信息科学与工程学院,上海 200237; 2.上海交通大学 塑性成形技术与装备研究院,上海 200030)

扩散焊是一种典型的固相连接方法,广泛应用于钛合金、铝合金、不锈钢等材料的焊接中[1]。但受扩散连接表面清洁程度较低、焊接工艺参数偏差等情况的影响,扩散焊连接界面处很容易出现不同程度的未焊合、弱结合等缺陷,因此对扩散焊进行可靠的质量检测具有非常重要的意义[2]。目前,扩散焊的无损检测多采用超声C扫描技术[3]。Kumar等[4]使用超声C扫描技术对不同扩散焊工艺进行超声检测,发现超声C扫描技术能够检测出部分焊合和未焊合区域;张弛等[5]通过改变检测参数,研究超声C扫描对于钛合金扩散焊小尺寸缺陷的检测能力,发现常规超声检测法很难对小尺寸缺陷进行精确的检测。

超声C扫描成像原理是使用机械扫查的方式采集、储存、分析各采样点的A扫信号,并通过灰度或伪彩色图像反映某一深度范围内的A扫信号的回波幅度[6]。但是常规超声C扫描图像的形成是通过在A扫信号中设置闸门,然后利用闸门内A扫信号的幅值信息进行成像来实现的。因此超声C扫描图像的形成与闸门位置有很大的关系,闸门位置不准确会直接影响超声C扫描图像的质量。此外,A扫信号易受噪声等外界因素的干扰,这也会影响超声C扫描图像的质量。尤其是扩散焊界面含有微小缺陷时,A信号的回波幅值会相对较小,超声C扫描图像在形成的过程中会受各种因素的干扰,导致微小缺陷不能很好地在超声C扫描图像中呈现出来。

针对该问题,本文提出基于小波变换的扩散焊超声C图像融合算法,将不同扫描点信号进行成像,提取多幅含有缺陷的超声C图像,利用基于小波变换的图像融合方法,综合多幅超声C图像中的缺陷信息,从而获得包含微小缺陷信息在内的融合结果图像。

1 原理与方法

1.1 基于小波变换的图像融合

基于小波变换的图像融合方法是利用小波变换的多分辨率分析将每个源图像分解为低频和高频部分,得到各个源图像的小波金字塔;然后使用不同的融合规则,分别对低频和高频部分进行融合处理得到新的小波金字塔结构,最后对处理后的小波系数进行小波逆变换,获得最终的融合结果[7]。

1.2 引导滤波

引导滤波器是一种基于局部线性模型的边缘保持器,它能够在平滑图像的同时,有效地保持图像的边缘信息[8]。引导滤波器的关键是引导图像I和滤波器输出q之间的局部线性模型,假设q为以像素k为中心的窗口ωk中关于I的线性变换:

qi=akIi+bk,∀i∈ωk。

(1)

式中:ak和bk为窗口ωk内的线性系数。

为确定线性系数ak和bk,同时需要满足滤波器的输出q和滤波器的输入图像p之间的差异最小,定义以下成本函数,使该成本函数最小:

(2)

式中:ε为调节滤波器滤波效果的参数;pi为输入图像p在位置i处的像素值;ak和bk可以通过式(3)的线性回归方法求解:

(3)

接下来,在整个图像的所有局部窗口中使用该线性模型来计算每个ωk窗口的线性系数。由于像素i会包含在不同的ωk窗口中,因此在计算所有ωk窗口的ak和bk后,取其平均得到最后的输出值:

(4)

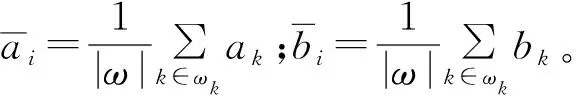
2 超声C图像融合算法

2.1 低频系数的融合

小波分解后的低频部分主要包含图像的结构、亮度、对比度等信息。低频分量的融合方法通常采用系数直接取平均法,这种方法虽然简单高效,但是没有考虑系数之间的关系,同时会降低图像的对比度,并且会导致信息的丢失[9]。为了保证在融合过程中尽可能减少信息的丢失,本文采用基于邻域系数局部方差加权求和的方法,定义邻域系数的局部方差为

(5)

式中:M和N分别为邻域窗口的长和宽;L(x,y)为邻域中各点的小波系数;μ为邻域中所有小波系数的均值。

邻域的方差越大说明小波系数的变化越大,该邻域的信息量也就越大,应该赋予更高的权重。设σA(x,y)和σB(x,y)分别表示源图像A和B以(x,y)为中心的邻域方差,得到源图像A和B在各个位置处的权重值:

(6)

则融合后图像低频系数表示为

L*(x,y)=wALA(x,y)+wBLB(x,y)。

(7)

2.2 高频系数的融合

小波分解后的高频部分主要包含图像的边缘等细节特征,但图像的噪声往往也包含在图像的高频信息中[10]。为了在减少噪声干扰的同时更好地突出图像的高频信息,采用区域能量加权求和的方式进行高频系数的融合。同时为抑制背景噪声对融合效果的影响,利用引导滤波对融合后的高频分量进行平滑。

为了尽可能地保持原始图像的边缘特征,使用Sobel算子与局部区域内的图像做垂直和水平方向的卷积。同时为了避免丢失图像的信息,采用加权求和的方式综合待融合图像的高频信息。式(8)定义了局部区域能量,其值越大代表着局部区域的图像越清晰,反映的信息就越多,需要赋予更高的权重。

(8)

式中:M和N分别为窗口区域的长和宽;H(x,y)为窗口中各点的高频系数值;Sx和Sy分别为水平和垂直方向的Sobel算子。

对源图像A和B进行小波分解后可得3个方向上的高频系数,按照式(8)计算以每个位置为中心的窗口对应的区域能量,然后再分别计算源图像A和B在各个位置处的权重值:

(9)

(10)

利用引导滤波优化融合后3个方向的高频系数:

(11)

2.3 增强融合图像

实验发现融合后的超声C图像的对比度较低且很多细节处不够清晰。因此,需要对融合后的图像进行增强处理。本文选择同态滤波方法来实现增强。同态滤波基于照射-反射模型,是一种在频域中压缩图像亮度范围,同时增强图像对比度的方法[11]。图像可以表示为照射分量与反射分量的乘积,照射分量一般是在空间缓慢变化的,可看作为图像的低频部分;而反射分量往往倾向于突变,可看作为图像的高频部分[12]。根据这一特征,通常对图像进行傅里叶变换,将图像的低频部分与照射分量联系起来,高频部分与反射分量联系起来。图1为同态滤波算法的流程图[13]。

图1 同态滤波原理图Figure 1 Homomorphic filter schematic

由以上流程可以看出,传递函数H(u,v)控制着傅里叶变换的高频和低频分量。为达到图像增强的目的,传递函数在提高高频分量的同时也要抑制低频分量。根据这一特点,同态滤波器的传递函数一般根据高通滤波函数构造而成[14]。但是,由于传统的传递函数中包含的参数较多,需要同时调整多个参数才能达到最佳的增强效果。为了减少传递函数中的参数,并且保持增强效果不变,本文提出了一种改进的同态滤波传递函数,该传递函数是基于S型曲线进行改进的,S型曲线的方程可以表示为

(12)

式中:x为常数。图2为式(12)对应的函数曲线图。

图2 S型曲线图Figure 2 S-shaped graph

根据曲线方程可以构造出改进的传递函数为

(13)

式中:D(u,v)为距滤波器中心的距离;a、b为调整增强效果的参数。

根据以上分析,本文提出的基于小波变换的超声C图像融合算法的具体步骤如下。

步骤1 将待融合的超声C图像进行3层小波分解,得到各自的高、低频系数;

步骤2 对于低频系数,采用基于邻域系数局部方差加权求和的方法进行融合得到低频融合系数;

步骤3 对于高频系数,采用基于局部区域能量加权求和的方法和引导滤波算法进行融合,得到高频融合系数;

步骤4 对融合系数进行小波逆变换,最终得到融合图像;

步骤5 最后,对融合图像采用改进的同态滤波进行增强,得到结果图像。

3 实验过程与结果

3.1 样品制备

在实际焊接过程中,扩散焊工件会受焊接面清洁程度不高、焊接工艺参数偏差等情况的影响,从而产生不同程度的未焊合缺陷,其中也包括一些微小型的缺陷。由于实际航空件的测试成本太高,因此针对这些类型的缺陷,制备人工缺陷试样进行扩散焊连接实验。该类试样的具体制备方法如下:采用两块钛合金板进行扩散焊连接,在两块钛合金板之间放置一钛合金箔片,在钛合金箔片上使用氮化硼阻焊剂制造不同的形状来模拟缺陷,其中包括方形、圆形等尺寸较大的形状以及线形、弧形等尺寸较小的形状。采用正常的焊接工艺对其进行扩散焊连接,焊接完成后喷涂氮化硼的位置会形成不同程度的未焊合缺陷。图3(a)为含有微小缺陷的人工试样图,该试样中包含方形、圆形和线形等多种形状的缺陷。其中方形缺陷的边长为10 mm,圆形缺陷的直径为10 mm,方形和圆形之间为喷涂氮化硼而形成的微小线形缺陷。

图3 人工试样和超声C扫描图像Figure 3 Artificial specimen and ultrasound C image

3.2 实验设计与分析

针对焊接后的人工缺陷试样,采用水浸式超声C扫描系统对其进行扫查,得到如图3(b)所示的超声C扫描图像,将其与图3(a)所示的人工缺陷试样实物图对比发现,超声C扫描图像仅能反映出部分缺陷信息,特别是图3(a)中位置4和位置6处的线形微小缺陷不能被检测出来。

进行超声C图像融合的第一步,就是对超声数据进行预处理,获得待融合图像。图4为含有未焊合缺陷的超声A扫信号。对于未焊合缺陷,超声回波的幅度会有明显的增强,也就是在A扫信号中会呈现突变的特征。因此使用小波变换的方法对未焊合区的A扫信号进行突变点检测[15],定位缺陷在A扫信号中的位置。通过分析发现,缺陷所在的位置为信号中第2个突变点的位置,即t=334 μs。

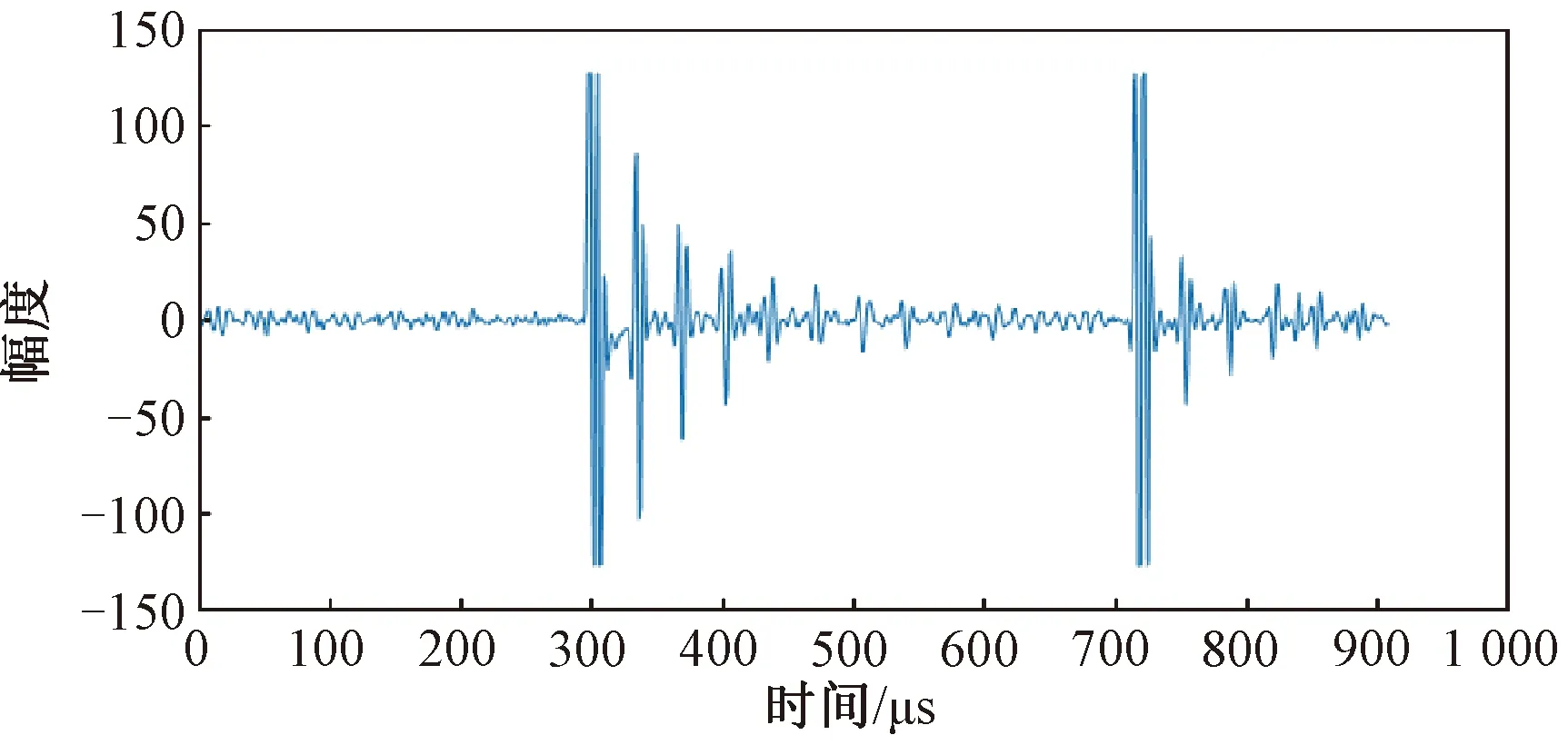
图4 未焊合缺陷超声A扫信号Figure 4 A scan signal of unwelded defects

由于缺陷信息会存在于不同切面的超声C图像中,于是提取所有采样点的A扫信号在t=334 μs和t=335 μs处的幅值,形成待融合的超声C图像,如图5(a)、5(b)所示。可以看出,使用超声信号的幅值所直接获得的超声C图像对比度较低且细节不清晰。为了观察待融合图像的细节特征,使用改进后的同态滤波算法对待融合图像进行增强,如图5(c)、5(d)所示。可以看出,经过同态滤波增强处理后的超声C图像对比度有明显的提升,也能看到更多的细节信息,并且两幅图像中包含的缺陷信息具有差异性和互补性。此外,增强后待融合的超声C图像含有明显的背景噪声,因此在融合过程中,对图像进行平滑处理是非常重要的步骤。

图5 待融合图像和融合结果图Figure 5 The image to be fused and the fusion result image

对待融合的超声C图像使用基于小波变换的超声C图像融合算法进行融合,得到最后的结果图如图5(e)所示。可以看出,本文算法重构出的结果图能够反映出更多的缺陷信息,特别是其中的微小线形缺陷,与实际的缺陷大小更接近。

为验证引导滤波在平滑图像和保持图像边缘方面的优势,进行如下对比实验:在融合过程中不使用滤波进行平滑,使用中值滤波和双边滤波进行平滑处理,得到的效果图如图6所示。可以看出,融合过程中不进行平滑处理获得的融合图像仍然包含背景噪声;对于使用中值滤波得到的结果图,其图像整体比较模糊,且不能保持原始图像的轮廓;使用双边滤波得到的结果图,虽然一定程度上抑制了背景噪声,但在图像的边缘保持上不及本文算法,而且对于使用双边滤波得到的结果图,其图像会因为过于平滑而导致部分细节信息的丢失。

图6 不同滤波算法效果图Figure 6 The effect images of different filtering algorithm

对不同平滑算法得到的结果图,本文使用平均梯度和峰值信噪比(PSNR)作为客观评价指标,对实验产生的结果图进行评价,结果如表1所示。通过对各客观评价指标的结果比对,可知经过本文算法平滑处理的结果图在平均梯度和峰值信噪比方面都优于其他算法。

表1 平滑效果对比Table 1 Smooth effect comparison

为验证本文算法检测微小缺陷的准确性,将图3(a)的人工缺陷试样、常规超声C扫描图像以及本文算法重构的结果图像中的线形缺陷的长度进行对比。对于人工缺陷试样,位置3～6处线形缺陷的长度分别为11、12、12、13 mm。常规超声C扫描图像检测出位置3和位置4处的缺陷长度为10 mm和6 mm,而对于位置5和位置6处的线形缺陷,在超声C扫描图像中则不能显示。使用本文算法重构的结果图中,位置3～6处的线形缺陷的长度分别为11、10、3、8 mm。基于以上分析可以发现,本文算法重构的超声C图像能够更为准确地反映线形微小缺陷信息。

另外,制备多组含有线形缺陷的人工试样进行实验,并计算不同方法下的平均误差:

(14)

式中:n为缺陷总数量;δi为第i个线形缺陷的实测长度与实际长度之间的误差。

制备5组人工试样,线形缺陷的总数量为30个,分别使用常规超声C扫描和本文算法进行检测,并计算平均误差。其中常规超声C扫描图像的平均误差为8 mm,本文算法重构出的超声C图像平均误差为2 mm。测试结果表明,本文算法重构出的超声C图像检测出的缺陷平均误差更小。

为进一步论证本文算法对微小缺陷检测的准确性,制备含有弱结合缺陷的试样进行实验。图7(a)为常规的超声C扫描图像,图7(b)为本文算法重构的超声C图像。可以看出,本文算法重构的超声C图像能够反映出更多的缺陷信息。其中,位置1和位置2为金相微观观察位置,实际缺陷长度分别为12.0 mm和13.5 mm。表2为缺陷长度对比表,从中可以看出,常规超声C扫描图像在位置1和位置2处检测到缺陷长度分别为10.0 mm和8.0 mm,而本文算法重构的超声C图像能够检测出的缺陷长度分别为12.0 mm和11.5 mm。本文算法重构出的结果图中的缺陷尺寸与人工试样的实际缺陷尺寸更相近。

表2 微观观察位置的缺陷长度对比Table 2 Comparison of defect lengths at microscopic observation positions

图7 弱结合缺陷检测结果图Figure 7 Weak bond defect detection image

针对弱结合缺陷,制备多组人工缺陷试样,并在每个试样中设置多个微观观察位置,并根据式(14)计算平均误差,对于弱结合缺陷的平均误差计算,n表示微观观察位置的数量,δi表示第i个位置缺陷的实测长度与实际长度之间的误差。由计算结果可知,常规超声C扫描图像对弱结合缺陷检测的平均误差为9.5 mm,而本文算法重构出的超声C图像的平均误差为4.2 mm。

4 结论

本文提出基于小波变换的超声融合算法,对不同C扫描点的信号进行成像,形成待融合的超声C图像,使用基于小波变换的图像融合方法,并结合引导滤波对待融合的超声C图像进行平滑处理得到融合图像;最后为提高融合图像对比度、丰富图像细节信息,使用改进的同态滤波器对图像进行增强,从而获得包含微小缺陷信息在内的融合结果图像。通过制备人工缺陷试样,将常规超声C扫描图像、本文算法重构的超声C图像与实际缺陷尺寸进行对比分析。实验结果表明:使用本文算法重构出的超声C图像,背景噪声得到了有效的抑制,并且能够更为准确地反映出缺陷信息。