基于广域部署智能反射面的无人机集群跟踪方法
2023-07-10郑磊陈志敏贾宇轩
郑磊,陈志敏,贾宇轩
(1.上海电机学院 电子信息学院,上海 201306;2.山东财经大学 管理科学与工程学院,山东 济南 250014)
0 引言
随着无人机技术的飞速发展,无人机现已广泛应用于军事和民用领域[1]。其中,在军事领域可用于侦查监视、对地攻击、目标追踪等;在民用领域可以用于环境监测、气象观测、灾难救援、航拍、电力巡检以及快递运输等。伴随着无人机技术的成熟,对无人机的探测和监管也成为一个重要问题。作为“低慢小”类飞行器,对无人机的探测难度很大。以常规无人机为例,其飞行在1 000 m以下区域,若使用雷达对其进行探测,则极易受建筑物、树木和鸟类等的干扰,环境噪声、信号衰减和遮挡等因素会严重降低探测跟踪性能,并且无人机具有慢速、悬停等特性,探测其产生的微多普勒频移也是一项严峻的挑战[2]。尤其在复杂城市环境中,电磁干扰和建筑物遮挡使得传统雷达等高价值设备定位跟踪低慢小目标困难,且容易丢失目标,经济代价很高。
本文针对在密集建筑环境下的多目标跟踪问题,提出一种基于智能反射面(IRS)[3-5]的多目标跟踪算法。IRS是由大量低成本、无源反射元所构成的平面,是一种可数字控制的二维超电磁材料所制成,通过设置相应的偏置电压,可以独立实现IRS反射单元的不同相移,改变元件中电阻值可以控制反射振幅,因此每个反射元均可独立控制入射信号的幅度/相位变化。另外,IRS可以仅被动反射入射信号,无需配置发射射频链路,因此与传统的有源天线阵列相比,利用IRS进行目标探测跟踪所需的硬件成本和能耗更低,且其本身由低成本电磁材料组成,成本更低。IRS具有轻便的几何结构,可以很容易安装在环境对象上或从环境对象上移除、替换,适合大规模部署。利用IRS低成本易于共形的特点,可以大量布设在城市建筑物的表面或顶部,这样即使目标被墙体遮挡,雷达发出的探测信号还可以通过IRS反射来探测目标。
使用IRS辅助探测,使用的电磁波通常工作在毫米波段,频率高、波长短,实际上探测距离由雷达的发射功率、载波波长、天线增益、天线接收面积和目标的雷达截面积决定,由于经过IRS的二次反射,有效的天线接收面积变小,会有一定的反射能量损失,作用距离会比传统的相控阵雷达短一些,且在复杂城市环境中易受障碍物遮挡影响。因此,可搭建图1所示场景,借助IRS转发发射端探测信号[6-8],克服建筑物遮挡的问题;同时,IRS接收目标回波,并将其转发给接收端,接收端进行信号处理后实现对多目标的定位。通过IRS灵活地控制发射和接收之间的无线信道,以实现理想的信号传播环境,有效地解决了信号传播中干扰的问题。
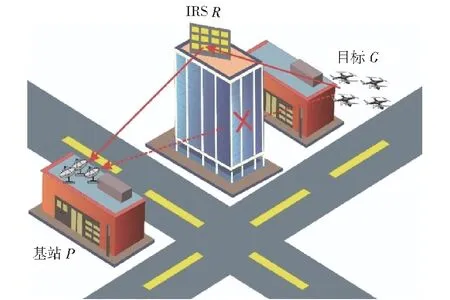
图1 多目标跟踪场景Fig.1 Multi-target tracking scenario
基于以上场景,本文提出一种基于模糊聚类特征辅助的多目标跟踪算法。在进行多目标跟踪时,目标相距较近,受到空间中噪声和系统噪声的影响,很难从一次扫描中得出哪个量测数据来源于哪个目标[9]。首先利用模糊C均值聚类(FCM)将观测到的点迹根据目标个数进行聚类,聚类的目的就是将所有量测数据进行分类,分辨出每一个目标对应的量测数据,然后将处理后的数据即分类好的量测数据与目标航迹进行关联[10]。航迹关联的目的是选取与目标预测数据最接近的关联数据,数据关联时,为了提高准确度,将一部分的历史数据中包含的特征信息如速度存储下来,作为筛选最接近于真实量测的阈值,最后将预测值和量测值输入卡尔曼滤波来跟踪目标的轨迹。
1 信号模型与运动模型
1.1 信号模型
目前针对多目标定位的算法主要分为两类:一类是扩展型目标定位,在雷达分辨率较低、无法成功分辨出每个目标时,可以看作一个整体,将其建模为扩展型目标进行跟踪定位;另一类是通过提高探测雷达的孔径和阵元数量,利用高分辨方式分辨出每个目标,再进行单目标跟踪[11]。本文采用扩展型目标定位算法,在雷达接收到的数据中将数据与目标一一关联起来,形成目标与量测数据对。无人机通过飞行控制,对其跟踪的难点就是飞行密度高、速度快和悬停以及交叉飞行或平行飞行,容易漏跟、误跟,难以分辨出每一个目标[12]。考虑图1所示的场景,假设目标在某水平面内运动,探测信号由基站P发出,经过R点处的IRS反射,可以探测到墙体后原本探测不到的目标G,回波信号通过IRS波束赋形后指向P,由P点处的接收端接收[13-14]。整个探测路径可以表示为P→R→G→R→P,则基站P在t时刻的发射信号X(t)为
X(t)=aH(θp,φp)s(t)ej2πf0t
(1)
式中:aH为发射端阵列指向矢量;θp表示发射端到IRS的方位角;φp表示发射端到IRS的俯仰角;s(t)表示信号的包络;f0为发射信号的载波频率。
将IRS放置在Oxz平面中,θ为回波信号到达反射单元的方位角,φ为回波信号到达反射单元的俯仰角,如图2所示。
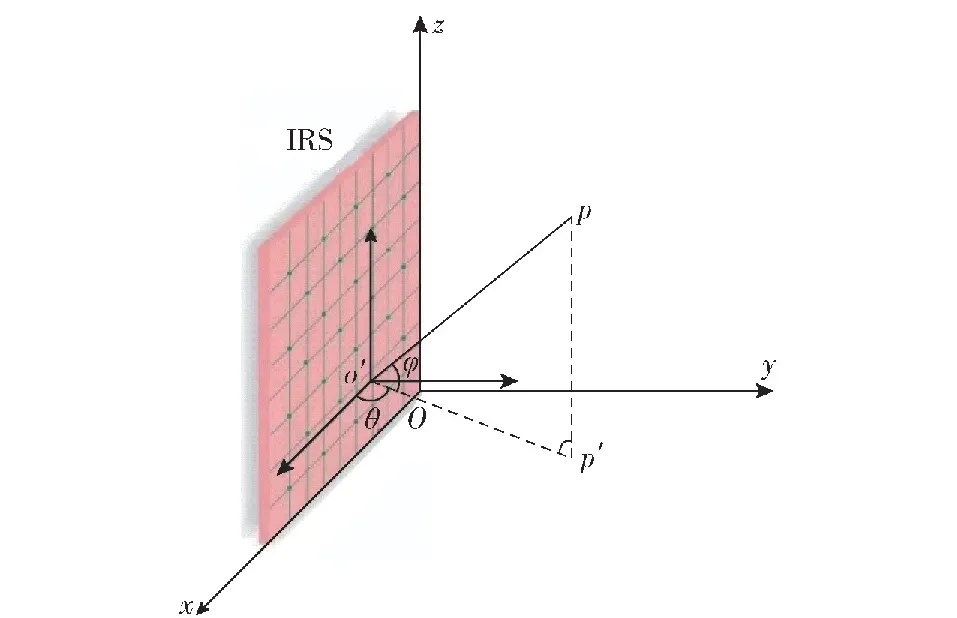
图2 IRS阵列响应Fig.2 IRS array response
假设p点处有一空间远场目标,探测信号探测到目标后会产生回波,回波由IRS再反射回接收端。设p在Oxy平面的投影为p′,o′为第m个反射单元的位置,则回波信号在第m个反射单元相对于原点的时延τm为
(2)
式中:xm、ym、zm为第m个反射单元在三维坐标系中的坐标值;c为电磁波速度。则参与反射的反射单元所产生的相移为

(3)
式中:f为探测信号的频率;λ为探测信号波长。
经IRS反射后的信号可以表示为
XRIS(t)=ΦX(t)
(4)
Φ=diag[β1ejφ1(θ,φ),β2ejφ2(θ,φ),…,βmejφm(θ,φ),…,βnejφn(θ,φ)]
(5)
式中:Φ为IRS反射的相移函数;βmejφm(θ,φ)为第m个反射单元的相移函数,βm为幅值,φm(θ,φ)为IRS的导向矢量;n为反射单元数量。
回波信号返回IRS时,假设有ks路信号到达反射面,此时有ks个反射单元反射回波信号,由天线接收端接收,假设天线接收端有N根天线,则第N个天线的接收信号可以表示为
YN(t)=βksejφks(θ,φ)XRIS(t-τN)ej2πfd(t-τN)
(6)
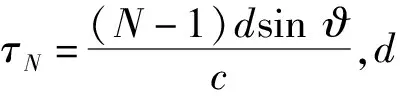
将图1场景构建到平面直角坐标系中,如图3所示。图3中,α为目标与IRS的夹角,β为发射基站与IRS的夹角,L为基站到IRS的距离。
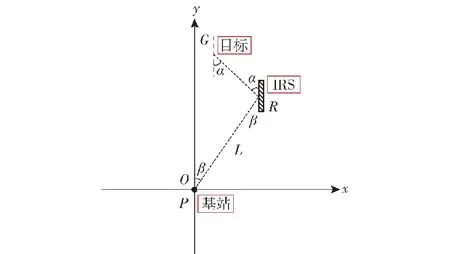
图3 IRS平面示意图Fig.3 IRS plane diagram
利用回波信号可以通过目标的俯仰角与IRS和发射雷达的距离等信息分析出目标的位置,通过多普勒频移得到目标的速度特征信息。空域内目标大多都是在三维空间内运动,为更直观表现出目标做交叉运动时跟踪算法的性能,将其简化为二维平面的运动,信号从发射到接收的时延为τ,则目标与RIS的距离为
(7)
假设目标是在Oxy平面水平运动,以接收阵列为坐标原点,则待跟踪的目标坐标为
(8)
目标运动产生多普勒频移:
(9)
式中:vr为雷达与目标间的径向速度;λ为载波波长。
因此目标的径向速度为
(10)
则目标在x轴、y轴方向的速度可以分解为
(11)
根据RIS反射回波信号可以得到目标的状态信息,则可以利用这些信息对观测数据进行数据关联。
1.2 运动模型
多目标跟踪的目的就是通过目标跟踪滤波器将探测到的点迹信息进行滤波处理,估计目标的运动轨迹并预测下一时刻目标的空间位置,从而实现对目标的持续跟踪,利用卡尔曼滤波算法对多个目标进行跟踪[15-17]。假设两个目标做匀速运动,则目标的匀速运动模型可以表示如下:
状态估计:
(12)
观测:
Zk=HkXk-1+vk
(13)
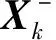
(14)
(15)
(16)
第i个目标得到目标的状态信息和量测信息,利用卡尔曼滤波对目标进行预测,则目标先验误差协方差矩阵为
(17)
式中:A为状态转移矩阵;Pk-1为k-1时刻先验估计误差协方差矩阵。
傍晚时分,一盏孔明灯在白家湾大队部门前徐徐上升,这是警报信号,看到这个信号,白家湾的民兵们拿的拿扁担,操的操棍棒,如马蜂出窝一般出发了,果不出招财营长所料,他们一个个争先恐后直往山上狂奔。健保、牛伢几个调皮角色一边跑一边唱着自编的歌曲,革命军人个个要老婆,一个两个不呀不为多,三个四个奈呀么奈得何,五个六个政府不许可。
卡尔曼增益为
(18)
式中:H为观测矩阵。
卡尔曼滤波方程为
(19)
得到Xk即为目标的预测信息。最后更新先验误差协方差矩阵,代入下一次的滤波计算中。
(20)
式中:I为单位矩阵。
卡尔曼滤波算法是一种基于线性状态方程及观测方程的经典目标跟踪算法,特点是不需要保存过去的量测数据,只需要根据新的数据以及前一时刻的估计值,借助系统本身的状态转移方程,以递归的方式,即可得到新的估计值。
2 基于模糊数据关联的特征辅助关联算法
多目标跟踪的任务就是得到量测数据后,对真假点迹和真假航迹的识别和分类,即在对目标进行跟踪时需要将量测到的数据与航迹进行匹配,形成真点迹与真航迹的配对[18]。现有的经典数据关联算法有最近邻域(NN)算法[19]和概率数据关联(PDA)算法[20]等,NN算法的基本思想是设置一个波门,使得量测值以一个较高的接收概率落入波门内,在相关波门中的若干候选回波中选择距离被跟踪目标的预测位置最近的回波作为目标回波。PDA算法认为落入相关波门内的回波都有可能源于目标,只是每个有效回波源于目标的概率不同,该算法利用相关波门内的所有回波以获得可能的后验信息,并根据大量的相关计算给出各概率加权系数及其加权和,将各个候选回波的加权和作为等效回波,利用它来更新目标的状态[21]。模糊数据关联(FDA)算法借助模糊聚类的方法,将数据进行分类,并得到每个数据的隶属度值,隶属度值表示了数据与目标之间的相似程度,相似程度越大表明这个量测数据越接近此航迹的真实量测,隶属度值类似于PDA算法中各个回波来自目标的概率。FDA算法是以FCM算法为基础的,FCM算法的根本目的就是将已知的数据分为若干类,使得目标函数达到最小,以得到最优聚类中心以及最优模糊矩阵。将目标的预测值设定为聚类中心,当前的量测值即为需要分类的数据,由于多目标跟踪下的量测点迹无法确认属于哪一个跟踪目标,因此需要在滤波前将所有的点迹正确归于要跟踪的目标,这个过程就是数据关联,完成关联后的量测数据与各个对应目标利用卡尔曼滤波即可得到相应的状态估计值。
2.1 FDA算法
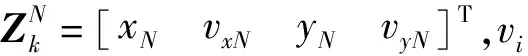
(21)
式中:C为聚类中心数目,即待跟踪的目标数;diz、djz分别表示第z个元素到第i个、第j个聚类中心的距离;l为加权指数(平滑因子);
隶属度矩阵中,相似度量可以表示为
diz=‖xz-vi‖
(22)
隶属度矩阵U表示为
(23)
隶属度矩阵U是点迹与航迹之间关联的基础,其中的每个元素就代表了点迹与航迹之间的相似度,将点迹与航迹进行关联的算法步骤具体如下:
算法1:FDA算法流程
输入:隶属度矩阵U,航迹个数C,量测数据Zk
初始化:k=0
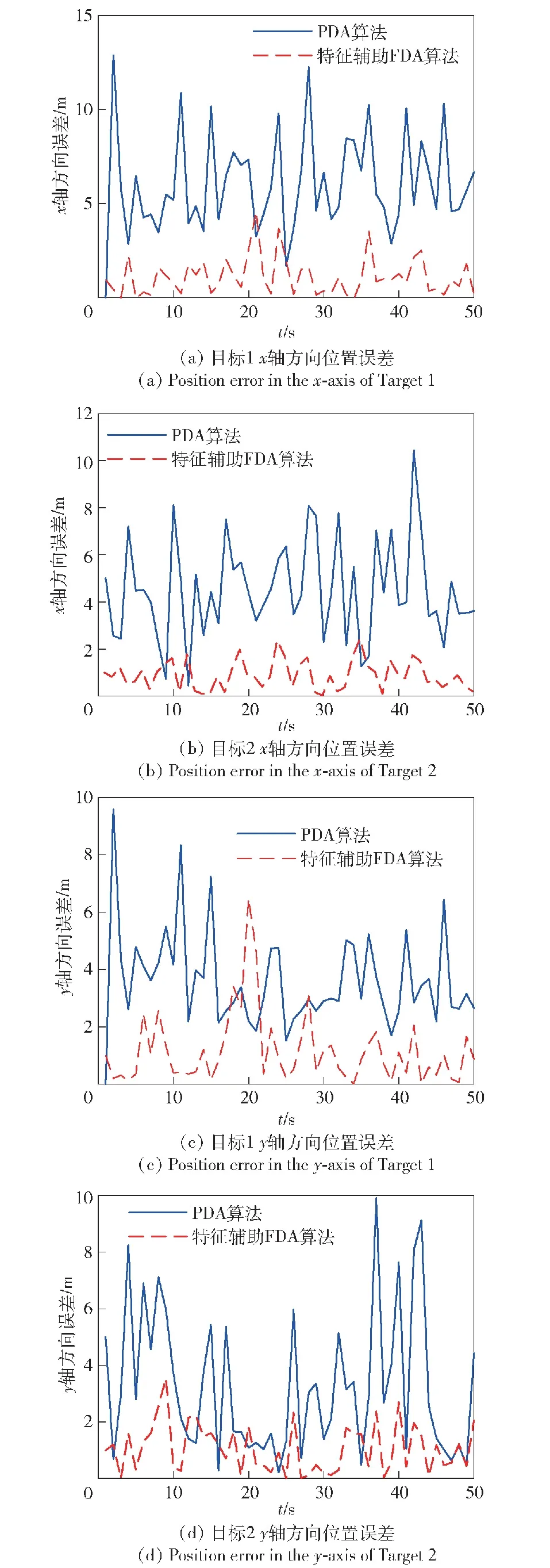
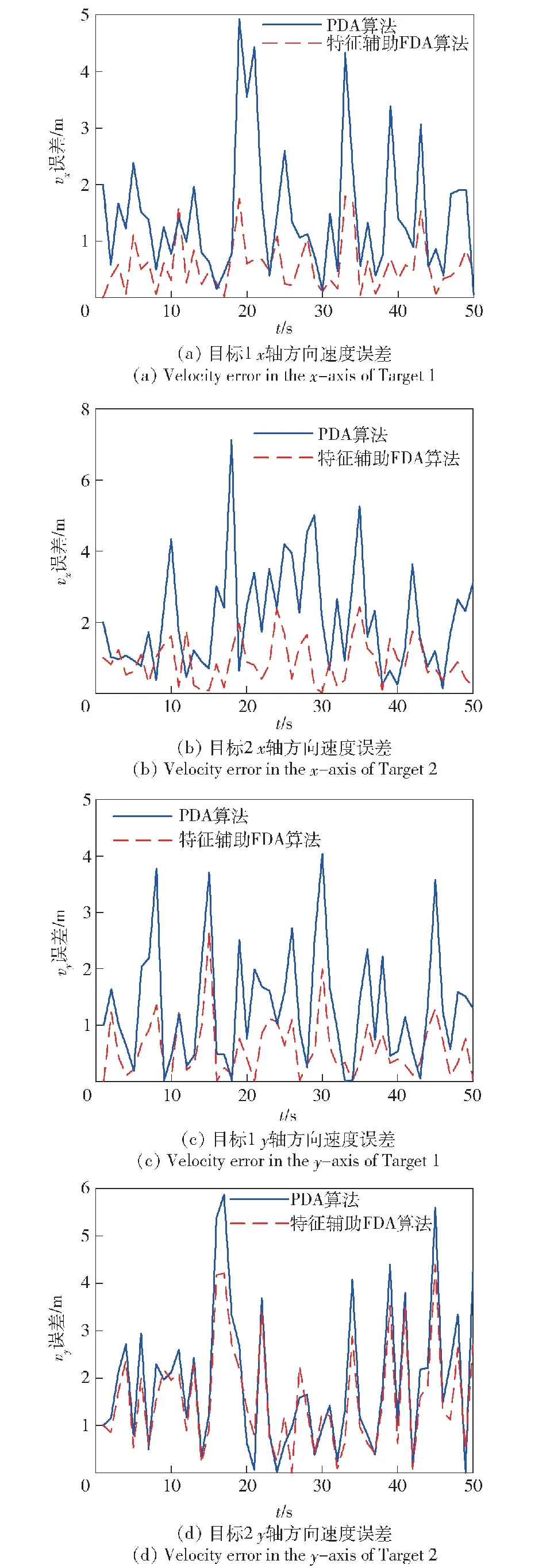
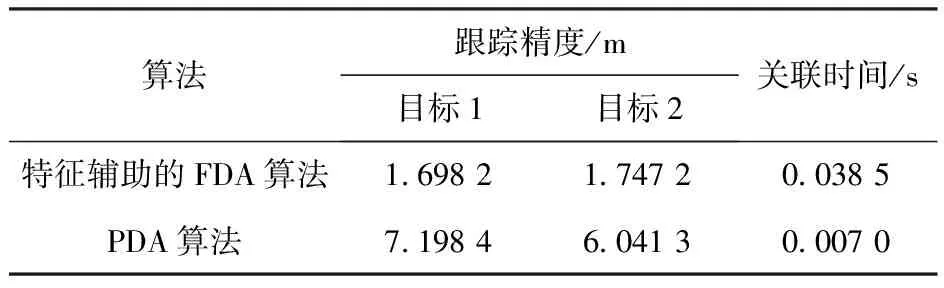
whilek Uij=arg maxU 删除U中Uij所在的行列,得到一个降维矩阵 k=k+1 end while 输出:C个目标与量测数据对 在密集杂波环境下,仅凭点迹与航迹之间的隶属度值依旧有可能关联错误,一旦出错就会对整个跟踪过程造成很大的影响,出现错误跟踪和错漏跟踪的现象,因此为了增加数据关联的正确性,在得到目标特征信息的基础上,提出了一种特征辅助的数据关联算法。 传统FDA算法是选取隶属度值最大的元素进行关联,在此基础上提出基于特征匹配的关联算法是对目标在当前时刻的位置信息以及速度特征信息同时进行预测,再将所有落入关联门限内的量测点迹进行筛选,最后选择匹配度最高的量测点迹进行关联[22-23]。 在特征信息的选取中,利用目标的一部分历史数据,即提取出目标在k-s时刻到k-1时刻的量测信息,s选取合适的数值,在相邻s帧的时间内,可以认为目标的速度特征是连续值且在短时间内不会发生剧烈的变化,不同的目标特征是不同的。这样将历史数据的均值作为目标在k时刻特征信息的预测值E,得到历史数据的标准差σ,标准差反映了量测数据偏离预测值的程度。本文提出一个筛选关联数据的阈值算法,设阈值为κ,若最大隶属度值对应的数据满足κ=[E-μσ,E+μσ],μ为权重因子,控制偏离预测值的程度,则可以将此量测数据与对应航迹进行关联,若不满足,剔除隶属度矩阵和量测数据中该隶属度值所在的行列,重新在新构造的隶属度矩阵中选取最大的隶属度值,并取得对应的量测数据重复以上步骤,进行关联。 不同的阈值决定了筛选有效量测数据的性能,决定目标跟踪的准确度和快速性,太小的阈值会使得跟踪算法过于敏感,容易产生空值;太大的阈值选取会使特征提取不明显,降低跟踪的准确度。s为特征提取的总帧数,帧数越多则阈值的判断区间更准确,但会增加存储数据的负担和算法处理的速度,因此根据实际情况总帧数选取为6,则将阈值从一个具体的值变为一个区间,增加了算法的自适应能力。 特征辅助的FDA算法具体步骤如下: 算法2:特征辅助的FDA算法流程 输入:隶属度矩阵U,航迹个数C,量测数据Zk,步长s 初始化k=0 whilek Uij=arg maxU Zk-s~Zk-1的数据求得其速度的均值E和标准差σ else 删除U中Uij所在的行列,得到一个降维矩阵 k=k+1 end while 输出:C个目标与量测数据对 为了验证本文算法在多目标跟踪中的有效性,研究多目标中的对象在做交叉运动时算法对做交叉运动的目标的跟踪性能,验证算法是否会产生错误跟踪、错漏跟踪现象。仿真给出了两个目标做交叉匀速运动的例子,对比各算法的均方根误差(RMSE)。目标真实轨迹的运动参数见表1。 表1 多目标运动参数Table 1 Multi-target motion parameters 图4 目标真实轨迹Fig.4 Real trajectory of the target 图4中的轨迹以基站为参考点,目标自左向右运动。由图4可见:本文算法用于多目标跟踪具有良好的跟踪性能,对于交叉目标的跟踪没有出现错误跟踪和错漏跟踪的现象,各目标航迹清晰可辩,和真实轨迹比较接近,不仅可以实现有效的数据关联,而且能够进行比较准确的状态估计,表明数据关联的成功;PDA算法跟踪的轨迹值相对于真实值有明显的偏离,当关联波门内的杂波和干扰较多时,偏离会更为明显。对比两种算法的位置误差和速度误差如图5和图6所示。 图5 目标位置误差Fig.5 Target position errors 图6 目标速度误差Fig.6 Target velocity errors 特征辅助的FDA跟踪算法在跟踪过程中,位置误差和速度误差都明显小于传统的PDA算法。在数据关联方面,特征辅助FDA算法利用运动目标的特征信息,对一部分历史数据求均值和方差,当作数据关联的阈值,使得滤波的数据十分接近真实值;而PDA算法首先计算波门内所有的回波来自于真实目标的概率,并对其进行加权,这样得到一个理论上的预测值,在目标航迹平行或者相交时会受到其他目标的干扰,造成加权求得的等效回波会明显偏离真实值。而特征辅助的FDA算法不计算等效回波,而是利用一部分的历史数据所得到的特征阈值,在聚类后的回波数据中按隶属度值从大到小地筛选出最接近真实值的回波数据,其位置与速度的均方根误差如表2所示。 从表2中可以看出,特征辅助的FDA算法在位置和速度方面的均方根误差更小,作为跟踪“低慢小”目标的跟踪算法,可以将多个目标进行区别,提高了关联的准确率。因为融合了目标运动的速度特征信息以及设定了筛选回波的阈值,且阈值会随着目标的运动自动进行调整,因此在进行数据关联时,可以关联到更加准确的量测数据,提高算法的关联准确性。表3给出了两种算法实验的统计结果对比,可以得出,特征辅助的FDA算法在跟踪精度上明显优于PDA算法,精度保持在2 m以内。 表3 两种算法实验统计结果Table 3 Statistical results of the two algorithms 本文提出一种基于IRS的特征辅助的多目标跟踪算法,该算法首先根据IRS在密集建筑群中的场景建立了对目标进行探测的信号模型,提出了多目标跟踪中最关键的数据关联模型,利用FDA将量测数据进行分类,再选取部分历史数据作为对目标特征的约束条件,设计了特征辅助的多目标跟踪算法。本算法能正确关联量测数据与目标,不会出现错误跟踪和错漏跟踪的现象;提高了跟踪精度,精度保持在2 m以内。仿真结果表明,该算法有效地提高了多目标数据关联的准确度。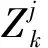
2.2 基于特征辅助的FDA算法
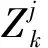
3 仿真实验



4 结论
